Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tuning the shape anisotropy of loosely bound colloid-like ionic clusters in solution†
Jana
Eisermann
 and
Dariush
Hinderberger
and
Dariush
Hinderberger
 *
*
Institute of Chemistry, Martin-Luther-Universität Halle-Wittenberg, Von-Danckelmann-Platz 4, 06120 Halle (Saale), Germany. E-mail: dariush.hinderberger@chemie.uni-halle.de; Fax: +49 (0) 345 55 27576; Tel: +49 (0) 345 55 25230
First published on 7th January 2019
Abstract
We characterize the influence of the ionic ratio on the dynamic self-assembly process involving a macrocyclic tetraimidazolium molecular box and small dianionic salts into highly defined, colloid-like ionic clusters in solution, called ionoids. Based on our studies utilizing dynamic light scattering (DLS) and continuous wave electron paramagnetic resonance (CW EPR) spectroscopy, we determine a region of privileged ionic ratios, which allow the formation of monodisperse, spheroidal structures of loosely bound ions in solution with adjustable (i) hydrodynamic radii between 6 nm and 12 nm and (ii) shape anisotropy. Inspired by Hertzsprung–Russell diagrams (HRDs) used in astrophysics to describe the fate of stars, we construct ionoid evolution diagrams (IEDs). IEDs are essential for grasping and describing the highly complex temporal development of these dynamically self-assembled structures in solution from the level of the individual ionic building blocks to stable clusters with a minimum lifetime of months, and thus aid in crafting future globular ionoids and anisotropic ionic clusters.
1 Introduction
Soft condensed matter comprises classes of materials like colloids, polymers, liquid crystals, amphiphiles, micelles and polyelectrolytes,1,2 not to mention the whole field of biological soft matter.3,4 These systems usually have structural length scales from one to several hundred nanometers and thus fall within the domain of ‘nanostructured materials’.1,5In recent publications,6,7 we characterized the formation of loosely bound ion-based colloid-like globular clusters of several nanometer size, termed globular ionoids. These structures, whose fabrication is based on the process of ionic self-assembly (ISA),8 represent a novel subclass inside the major field of supramolecular chemistry.9–11 Supramolecular chemistry in general aspires to the development of highly complex chemical systems from components interacting through noncovalent intermolecular forces. The ISA process in fact involves (i) electrostatic interactions as the primary driving force12 and (ii) weaker noncovalent interactions (such as solvation, hydrogen bonding, van der Waals etc.) as the secondary driving force.13
For the formation of a colloid-like ionic cluster, we combine the ‘Texas-sized molecular box’ (14+, Fig. 1), developed by Sessler and coworkers,14–16 with small dianionic salts (methanedisulfonate, 22− or Fremy's salt dianion, 32−, see Fig. 1) in our established solvent mixture of DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v).6,7 To obtain size monodisperse supramolecular structures due to long-range electrostatic correlation, a molar ratio of 14+
7 (v/v/v).6,7 To obtain size monodisperse supramolecular structures due to long-range electrostatic correlation, a molar ratio of 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− (14+
22− (14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32−, respectively) of 1 mM
32−, respectively) of 1 mM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mM is needed.6 Changes in solvent composition or ion concentration (while keeping the molar ratio of all ions constant), as highlighted in our previously performed studies, significantly affect the size, shape and stability of the self-assembled entities.7
3 mM is needed.6 Changes in solvent composition or ion concentration (while keeping the molar ratio of all ions constant), as highlighted in our previously performed studies, significantly affect the size, shape and stability of the self-assembled entities.7
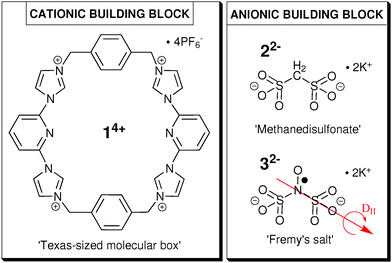 | ||
| Fig. 1 Molecular structure of cationic building block 14+ (left) and anionic building blocks 22− (top right) and 32− (bottom right). | ||
In this study, we investigate the influence of the ionic ratio of cationic and anionic building blocks (Fig. 1) on the self-assembly process in the optimal solvent mixture. We intend to point out the importance of cation–anion proportion as well as to define the optimal ionic ratio for the formation of globular ionoids. Furthermore, we can now extend our approach and create a variety of different self-assembled entities with anisotropic shape, anisotropic ionoids, containing 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− (14+
22− (14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32−, respectively), which possess the same durability as the archetypical globular ionoids introduced previously.
32−, respectively), which possess the same durability as the archetypical globular ionoids introduced previously.
2 Experimental
2.1 Materials
The ‘Texas-sized molecular box’ (14+) used in this study was synthesized according to the work of Sessler and coworkers14,16 as described in our previous studies.6,7 As small dianionic salts, we chose methanedisulfonic acid dipotassium salt (22−; Sigma-Aldrich, Munich, Germany) with purity ≥99% and Fremy's salt (potassium nitrosodisulfonate, 32−; Sigma-Aldrich) of technical grade. All chemicals were applied as received. For producing our established solvent mixture, we combined DMSO with ≤0.02% water (Sigma-Aldrich) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) ratio with 86–88 wt% glycerol (Acros Organics, Niderau, Germany). The concentration of 14+ was varied between 0 mM and 3 mM, while the amount of 22− (32−, respectively) was constant at 3 mM.
1 (v/v) ratio with 86–88 wt% glycerol (Acros Organics, Niderau, Germany). The concentration of 14+ was varied between 0 mM and 3 mM, while the amount of 22− (32−, respectively) was constant at 3 mM.
2.2 Ionic ratio
We compared the studied systems with our reference system containing 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− (14+
22− (14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32−, respectively) in a concentration ratio of 1 mM
32−, respectively) in a concentration ratio of 1 mM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mM. To study the influence of the ionic ratio on the dynamic self-assembly of ionoids, we systematically adjusted the concentration of our cationic building block, while keeping a constant concentration of the anionic component in each sample (see Table 1). This has the EPR spectroscopic advantage that all samples are directly comparable in EPR spectroscopy, as they have the same amount of radical 32− (see Fig. 1).
3 mM. To study the influence of the ionic ratio on the dynamic self-assembly of ionoids, we systematically adjusted the concentration of our cationic building block, while keeping a constant concentration of the anionic component in each sample (see Table 1). This has the EPR spectroscopic advantage that all samples are directly comparable in EPR spectroscopy, as they have the same amount of radical 32− (see Fig. 1).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− (14+
22− (14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32−, respectively) in DMSO
32−, respectively) in DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v) combined with their calculated ionic ratio
7 (v/v/v) combined with their calculated ionic ratio
Calculating the ionic ratio inside each 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− (14+
22− (14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32−, respectively) system is based on eqn (1)
32−, respectively) system is based on eqn (1)
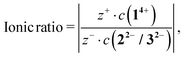 | (1) |
2.3 Methods
We used a Litesizer 500 (Anton Paar GmbH, Graz, Austria) for recording DLS. This device, which is also capable of measuring static light scattering, zeta potental, transmittance and refractive index, irradiates the sample with a 40 mW semiconductor laser at a typical wavelength of λ = 658 nm. An automatic configuration of the heatable optical bench allows perfected count rate traces. The choice between three different detection angles of back (175°), side (90°) and forward (15°) scattering allows measuring a broader range of samples and getting information on the potential geometrical anisotropy.22 Here, we studied our samples, which were filled into quartz cells (Hellma Analytics, Müllheim, Germany), utilizing back as well as side scattering at a fixed temperature of 20 °C.
Sample preparation was identical for all tested mixtures of Table 1. Before dissolving the compounds (see Fig. 1) in DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
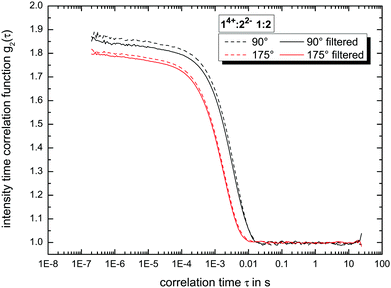
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v), we filtered the solvent using Millex filter units (hydrophilic LCR (PTFE)-membranes) with a pore-size of 450 nm. A second filtration step (with the same filter-type) was used to transfer the final solution into the measurement cell without any contamination such as dust.17 We measured all samples in regular, frequent intervals up to 79 days to get insight into their long-term stability. The resulting autocorrelation functions (see e.g.Fig. 3 as reference) were analyzed using the ALV-5000/E/EPP (v. 3.0.1.13, ALV-Laser-Vertriebsgesellschaft m. b. H. Langen, Germany) software. Further information about the calculation of the hydrodynamic radius is given in the ESI.†
7 (v/v/v), we filtered the solvent using Millex filter units (hydrophilic LCR (PTFE)-membranes) with a pore-size of 450 nm. A second filtration step (with the same filter-type) was used to transfer the final solution into the measurement cell without any contamination such as dust.17 We measured all samples in regular, frequent intervals up to 79 days to get insight into their long-term stability. The resulting autocorrelation functions (see e.g.Fig. 3 as reference) were analyzed using the ALV-5000/E/EPP (v. 3.0.1.13, ALV-Laser-Vertriebsgesellschaft m. b. H. Langen, Germany) software. Further information about the calculation of the hydrodynamic radius is given in the ESI.†
EPR techniques in general are highly sensitive as well as selective and can operate on structurally disordered materials.24,25 We focused on the change in the rotational motion, as quantified by either the rotational rate or correlation time τc, the anisotropies of rotational rates and the spectral line shape, to identify tendencies for ionic clusters. Spectral simulations were performed in Matlab (R2016a, v. 9.0) exploiting the EasySpin package (v. 5.2.11).26 The ESI† contains descriptions about the general simulation approach and sets of simulation parameters.
CW EPR measurements were performed at X-band (9.4 GHz) microwave frequencies with a Miniscope MS400 (magnettech, Berlin, Germany) benchtop spectrometer. For recording the spectra, we used a microwave power of 1 mW, a sweep width of 100 G and a modulation amplitude of 600 mG, while keeping the sample temperature at 20 °C with the temperature controller H03 (magnettech). A frequency counter (FC 400, magnettech) was used to record the microwave frequency. We additionally measured at higher frequencies/magnetic fields to improve the spectral (g-)resolution and to obtain a different view on rotational motion of the radicals. Therefore, we switched to Q-band frequencies (34 GHz) using a Bruker EMX-plus spectrometer with an ER5106QT resonator (Bruker Biospin GmbH, Reinstetten, Germany). Measuring at the same temperature compared to the X-band, the spectra were recorded with a microwave power of 1 mW, a sweep width of 130 G and a modulation amplitude of 1000 mG.
Sample preparation was similar for both X-band and Q-band EPR spectroscopy. About 10 μl to 15 μl of the samples was filled into small capillaries (Blaubrand, Wertheim, Germany) and capped with matching tube sealant (Leica Critoseal). All measurements were performed directly after preparation (day 0), since Fremy's salt in solution does not have a long-term stability at 20 °C.
3 Results and discussion
3.1 General remarks
As introduced in our previous study,7 we applied the following terms to describe the ionic self-assembly process for all measured systems:(i) globular ionoids: spherical, highly stable structures with a hydrodynamic radius between 6 nm and 8 nm
(ii) anisotropic ionic cluster: structures with deviations from a spherical structure and/or slightly extended dimensions
(iii) ion cloud: initial state after sample preparation with no globular structure and RH > 100 nm.
Note that we can employ CW EPR spectroscopy only for measuring the ion cloud state that forms in the initial hours after system preparation. This is due to the disproportionation of the EPR-active Fremy's salt dianion (32−) in solution proceeding faster than the ten-day incubation period of colloid-like ionic structures.
3.2 Analyzing ionic ratio dependence with DLS
As previously established,6,7 we used DLS to directly observe the development of ionic clusters, mainly through their scattering profiles and the thus derived hydrodynamic radius. As the dianionic compound, we used 22− due to its stability over the course of several months at 20 °C.
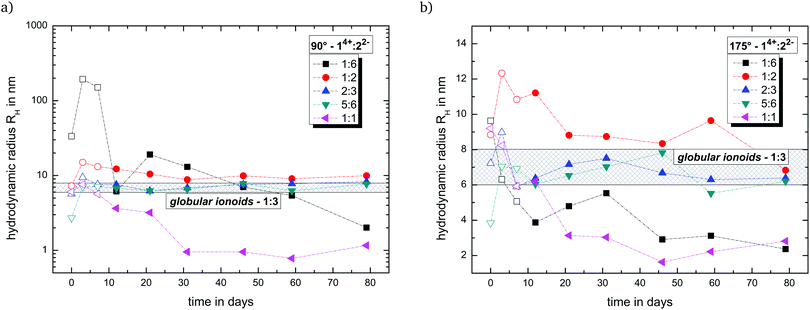
Fig. 2 summarizes the trend of the hydrodynamic radii with side and back scattering for all newly introduced molar ratios of 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− in DMSO
22− in DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v). Furthermore, we highlight the region for the globular ionoid size in the established 1
7 (v/v/v). Furthermore, we highlight the region for the globular ionoid size in the established 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-system, which is located between 6 nm and 8 nm.6,7 Note that we include the development of the hydrodynamic radius within the ten-day incubation period (open symbols in Fig. 2). During this incubation period, we can record autocorrelation functions with DLS, but the (i) mean scattering intensities are not significantly higher compared to the pure solvent mixture DMSO
3-system, which is located between 6 nm and 8 nm.6,7 Note that we include the development of the hydrodynamic radius within the ten-day incubation period (open symbols in Fig. 2). During this incubation period, we can record autocorrelation functions with DLS, but the (i) mean scattering intensities are not significantly higher compared to the pure solvent mixture DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water and (ii) the y-intercept values differ significantly between side and back scattering. After the incubation period, we obtained strongly pronounced intensity time correlation functions at measurement days 90° and 175° combined with stable count rate traces. This ten day incubation time is still enigmatic and will be discussed in a later publication.
water and (ii) the y-intercept values differ significantly between side and back scattering. After the incubation period, we obtained strongly pronounced intensity time correlation functions at measurement days 90° and 175° combined with stable count rate traces. This ten day incubation time is still enigmatic and will be discussed in a later publication.
Based on Fig. 2, the molar ratios 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 2
2, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 5
3 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 are able to build up at least anisotropic ionic clusters with similar dimensions as seen for the 1
6 are able to build up at least anisotropic ionic clusters with similar dimensions as seen for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio. The present deviations between side and back scattering indicate a more spheroidal shape compared to the almost perfectly spherical globular ionoids. In addition, these self-assembled structures have an inherent long-term stability, which is also visible in the intensity time correlation functions at measurement day 79 (see Fig. S1, ESI†). To further highlight the durability of our soft nanoscale structures in general, we filtered each sample again after a measuring period of 79 days and recorded the DLS scattering traces. Fig. 3 displays exemplary the autocorrelation functions for the molar ratio 14+
3 ratio. The present deviations between side and back scattering indicate a more spheroidal shape compared to the almost perfectly spherical globular ionoids. In addition, these self-assembled structures have an inherent long-term stability, which is also visible in the intensity time correlation functions at measurement day 79 (see Fig. S1, ESI†). To further highlight the durability of our soft nanoscale structures in general, we filtered each sample again after a measuring period of 79 days and recorded the DLS scattering traces. Fig. 3 displays exemplary the autocorrelation functions for the molar ratio 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− 1
22− 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 at both scattering angles. There is no significant difference visible between the DLS traces before and after filtration, indicating the unaltered size, shape and amount of ionic clusters inside the tested sample even after applying mechanical stress on to the self-assembled entities. The autocorrelation functions for all molar ratios are summarized in the ESI,† (see Fig. S2).
2 at both scattering angles. There is no significant difference visible between the DLS traces before and after filtration, indicating the unaltered size, shape and amount of ionic clusters inside the tested sample even after applying mechanical stress on to the self-assembled entities. The autocorrelation functions for all molar ratios are summarized in the ESI,† (see Fig. S2).
The other two tested molar ratios 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− 1
22− 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 and 1
6 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 do not show pronounced autocorrelation functions after 79 days and therefore no self-assembled structures with long-term stability. Note that in Fig. 2, these ratios display a similar time-dependent development of the hydrodynamic radius for the back scattering angle. Both mixtures are able to build up ion cloud structures (1
1 do not show pronounced autocorrelation functions after 79 days and therefore no self-assembled structures with long-term stability. Note that in Fig. 2, these ratios display a similar time-dependent development of the hydrodynamic radius for the back scattering angle. Both mixtures are able to build up ion cloud structures (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6) or even smaller entities (1
6) or even smaller entities (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) directly after sample preparation, but seem unable to transform this initial state into globular ionoids or anisotropic ionic clusters. A shortage or excess of 14+ fundamentally changes the ionic self-assembly process due to the disturbed interplay between long-range electrostatic correlations and weaker noncovalent interactions.
1) directly after sample preparation, but seem unable to transform this initial state into globular ionoids or anisotropic ionic clusters. A shortage or excess of 14+ fundamentally changes the ionic self-assembly process due to the disturbed interplay between long-range electrostatic correlations and weaker noncovalent interactions.
Based on the DLS data, only ionic ratios in the region of 2/3 to 5/3 (molar ratios 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 to 5
3 to 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6) are able to generate long-lived monodisperse, spheroidal colloid-like structures for the 14+
6) are able to generate long-lived monodisperse, spheroidal colloid-like structures for the 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− system in DMSO
22− system in DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v).
7 (v/v/v).
3.3 Analyzing ionic ratio dependence with CW EPR spectroscopy
After characterizing the 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− system by DLS, we continued with CW EPR spectroscopy, which requires exchanging the anion 22− with paramagnetic Fremy's salt dianion (32−). This can influence interactions inside the ion cloud, but electrostatic correlations especially to 14+ remain highly similar, as previously shown.6 To distinguish between the influence of solely (i) solvent viscosity and (ii) electrostatic interaction with increasing 14+ concentration on the rotational mobility of our spin probe, we measured 3 mM pure Fremy's salt in DMSO
22− system by DLS, we continued with CW EPR spectroscopy, which requires exchanging the anion 22− with paramagnetic Fremy's salt dianion (32−). This can influence interactions inside the ion cloud, but electrostatic correlations especially to 14+ remain highly similar, as previously shown.6 To distinguish between the influence of solely (i) solvent viscosity and (ii) electrostatic interaction with increasing 14+ concentration on the rotational mobility of our spin probe, we measured 3 mM pure Fremy's salt in DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v) as an internal reference (molar ratio 0
7 (v/v/v) as an internal reference (molar ratio 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in Table 1). Additional line broadening based on dipolar interactions between multiple radicals can be neglected due to the still pronounced and fast rotational motion of the radicals, which averages out the dipolar coupling.
1 in Table 1). Additional line broadening based on dipolar interactions between multiple radicals can be neglected due to the still pronounced and fast rotational motion of the radicals, which averages out the dipolar coupling.
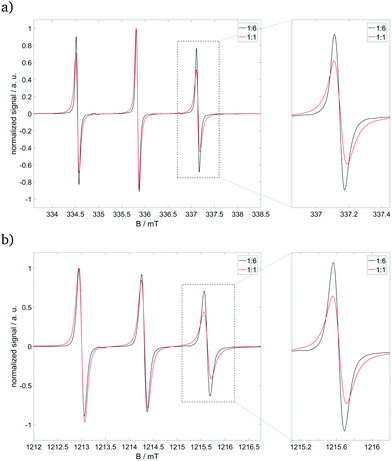
CW EPR spectra of the pure nitroxide radical (see ESI,† Fig. S3) in our established solvent mixture show rotational diffusion, which can be described by an axial tensor with the unique axis along the N–S-bond of Fremy's salt (see red arrow in Fig. 1).25,27 Rotation about this unique axis (D‖) is at least 35-fold faster than that about the axes perpendicular (D⊥) to it, in which deviations between X- and Q-band frequencies reflect the difference in frequency/field dependence of the rotational time-frame with higher frequencies/magnetic fields.27 Adding 14+ to our pure nitroxide radical (see Fig. 4) leads to (i) significant line broadening, mainly reflecting the slowed-down rotation around the molecular z-axis, and (ii) a shift of the unique D‖-axis from the N–S-bond towards the dissecting angle of both sulfonate groups. The strength of the first effect depends on the concentration of the cationic building block: For the molar ratio 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32− 1
32− 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6, Fremy's salt still rotates relatively freely, but also starts to favor certain coordinations due to the electrostatic attraction to 14+ and repulsion among the other 32− ions. At higher molar ratios, like 1
6, Fremy's salt still rotates relatively freely, but also starts to favor certain coordinations due to the electrostatic attraction to 14+ and repulsion among the other 32− ions. At higher molar ratios, like 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, Fremy's salt shows slowed-down rotation around the molecular z- and x-axes, indicating a more fixed coordination to 14+.
1, Fremy's salt shows slowed-down rotation around the molecular z- and x-axes, indicating a more fixed coordination to 14+.
To quantify the effect of increasing 14+ concentration on the rotational mobility of Fremy's salt, we combine different evaluation systems in the following:7
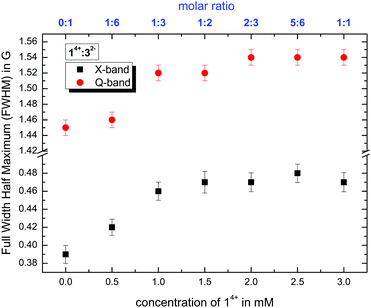
1. Analyzing the line width, where we use the full width at half maximum (FWHM) values of the CW EPR spectra by simulating isotropic broadening, which is implemented in the EasySpin program package. Note that this method does not assume that any physical model is causing the broadening (see Fig. 5).
2. Calculating the anisotropy T of the rotational diffusion tensor as
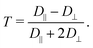 | (2) |
We mainly discuss this parameter that emphasizes the distinction between D‖ and D⊥ and characterizes the magnitude of electrostatic interactions in the direct vicinity of Fremy's salt in the ESI.†
3. As a very simple measure, the isotropic rotational correlation time τc can be calculated even in the case of (slight) anisotropy of rotational motion (see ESI†).
The FWHM values of each tested molar ratio of 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32− in DMSO
32− in DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v), as shown in Fig. 5, show the same tendencies at X- and Q-band frequencies. The steady increase in the line width correlates with higher amounts of 14+ and stronger electrostatic interactions with and subsequent slow-down of Fremy's salt. In addition, the coordination of both components shifts from a weak bond between 14+ and 32− at a molar ratio of 1
7 (v/v/v), as shown in Fig. 5, show the same tendencies at X- and Q-band frequencies. The steady increase in the line width correlates with higher amounts of 14+ and stronger electrostatic interactions with and subsequent slow-down of Fremy's salt. In addition, the coordination of both components shifts from a weak bond between 14+ and 32− at a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 to a more direct ion pair coordination at 1
6 to a more direct ion pair coordination at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. At a ratio of 1
1. At a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and higher, the FWHM values reach a plateau (within the margin of error), indicating that the local dynamic electrostatic attachment at day 0 of the ion mixtures (that are still in the ion cloud state, not the ionoid state) is similar above this ratio in the initial ion cloud state. Similar effects can be derived from the calculated rotational correlation time τc and the anisotropy T (see ESI,† Fig. S4). Note that through the frequency-dependent differences in time-frame sensitivity/averaging, the X-band spectra rather mirror the globally averaged interactions and dynamics, while the Q-band spectra highlight the interactions in the local environment of Fremy's salt.7
3 and higher, the FWHM values reach a plateau (within the margin of error), indicating that the local dynamic electrostatic attachment at day 0 of the ion mixtures (that are still in the ion cloud state, not the ionoid state) is similar above this ratio in the initial ion cloud state. Similar effects can be derived from the calculated rotational correlation time τc and the anisotropy T (see ESI,† Fig. S4). Note that through the frequency-dependent differences in time-frame sensitivity/averaging, the X-band spectra rather mirror the globally averaged interactions and dynamics, while the Q-band spectra highlight the interactions in the local environment of Fremy's salt.7
3.4 Ionoid evolution diagram (IED)
Inspired by the so called Hertzsprung–Russell diagrams (HRDs),‡ which are used in astrophysics to summarize and display the complex relationships of the properties of stars and stellar evolution during their complete lifetime of billions of years,28 we propose the construction of ionoid evolution diagrams (IEDs) for summarizing the fate (here up to 79 days) of the dynamic ionic self-assembly processes that range from large ion cloud states of several hundreds of nanometers, all the way down (in size) to ion pairs and globular or anisotropic ionic clusters as remarkably stable yet flexible entities in between. More specifically, we can even illustrate the ionic ratio influence on the formation of our highly defined structures, as shown in Fig. 6. Hertzsprung–Russell diagrams display the distribution of stars, sorted by their luminosity on the y-axis and their surface temperature on the x-axis. Mass and time development are thus implicitely part of HRDs. Hence, these diagrams allow summarizing and displaying all stages of stellar development, which is a remarkably large and complex set of data and we developed our IEDs to adapt this kind of data analysis as well as to describe the dynamic ionic self-assembly process inside our solutions, which also comprises a wealth of complex data and long temporal evolution.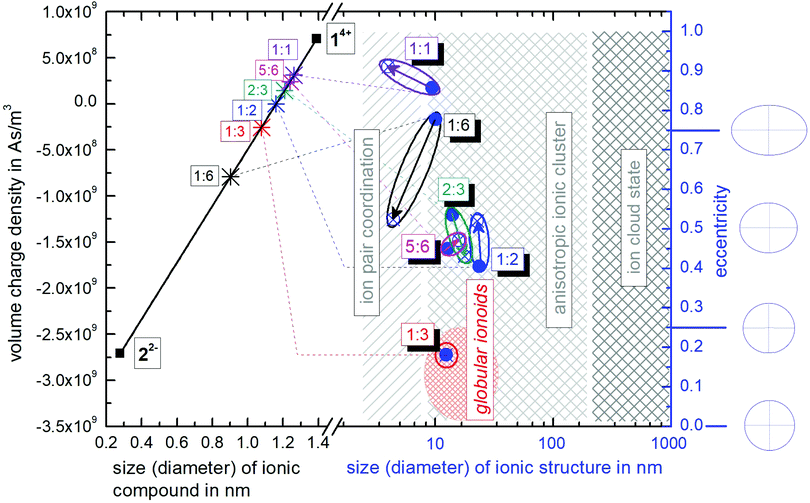 | ||
| Fig. 6 Ionoid evolution diagram for modifying the molar ratio between the ionic building blocks 14+ and 22−, highlighting the three states of the ionic self-assembly process: globular ionoids, anisotropic ionic clusters and ion cloud. A detailed explanation is given in the text and the ESI.† | ||
The left y-axis displays the volume charge density of the two building units, which could be calculated by dividing the charge z± (multiplied with the elementary charge e) of the cationic and anionic components by their respective volumes (see the ESI† for details). As the x-axis, we use the diameter of 14+ and 22− (without solvation shell) due to the importance of the size and size ratio of the anionic and cationic components for the self-assembly process. By simply changing the molar ratio of 14+ and 22−, we are able to adjust the resulting volume charge density as well as the acting electrostatic correlations29 along the black connecting line of both ions (this resembles the main sequence line in Hertzsprung–Russell diagrams, see the ESI† or ref. 28). Starting from these intersections, we plot on the right y-axis the eccentricity 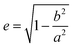 § to define deviations from a perfect sphere (with a value of e = 0) versus the final size of the ionic cluster based on the utilized molar ratios of 14+
§ to define deviations from a perfect sphere (with a value of e = 0) versus the final size of the ionic cluster based on the utilized molar ratios of 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22−, illustrating the durability of more or less spherical self-assembled entities. In Fig. 6, we also plot the two-dimensional forms representing the eccentricities e = 0, e = 0.25, e = 0.50 and e = 0.75 to demonstrate the transition from a circular to an elliptical shape. A representation with three-dimensional structures can be found in the ESI,† (see Fig. S6). We further include the time beginning from the complete incubation period of ten days (blue full dots) until the last measurement day (arrow to blue crossed dots).
22−, illustrating the durability of more or less spherical self-assembled entities. In Fig. 6, we also plot the two-dimensional forms representing the eccentricities e = 0, e = 0.25, e = 0.50 and e = 0.75 to demonstrate the transition from a circular to an elliptical shape. A representation with three-dimensional structures can be found in the ESI,† (see Fig. S6). We further include the time beginning from the complete incubation period of ten days (blue full dots) until the last measurement day (arrow to blue crossed dots).
In Hertzsprung–Russell diagrams, the temporal evolution of billions of years is implicitly shown by deviations from the main sequence. Evolution with time is emphasized in IEDs by the oval (or for globular ionoids, more circular) frame. Note that for our systems, we obviously do not observe the same time frame of billions of years. However, if we normalize the ionic self-assembly process to a crucial time step, which, e.g., could be the translational and rotational diffusion of our ionic building blocks in solution, we can recalculate the required time steps in unit time needed to form stable ionic clusters. As a fast limit for the unit time step for the following estimations, we chose 1 ns for the diffusion itself. Hence, the experimentally found incubation time of ten days for globular ionoids in unit time steps can be estimated, too. One day amounts to 86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s or 8.64 × 1013 ns, leading to a total number of 8.64 × 1014 ns for ten days, in which the self-assembled entities form. Thereby, our building units have to experience billions of diffusion steps to gain a stable yet flexible structure.
000 s or 8.64 × 1013 ns, leading to a total number of 8.64 × 1014 ns for ten days, in which the self-assembled entities form. Thereby, our building units have to experience billions of diffusion steps to gain a stable yet flexible structure.
As visualized in the IED (Fig. 6), we deduce the following for the 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− system:
22− system:
1. Molar ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 builds up initial ionic structures with significant deviations from a spherical shape, which, over time, decompose into smaller ion pair coordinations. Note that the setup of this mixture with a high amount of small anions compared to the large ‘Texas-sized molecular box’ is similar to polyelectrolytes, e.g., PDADMAC.24,25,30
6 builds up initial ionic structures with significant deviations from a spherical shape, which, over time, decompose into smaller ion pair coordinations. Note that the setup of this mixture with a high amount of small anions compared to the large ‘Texas-sized molecular box’ is similar to polyelectrolytes, e.g., PDADMAC.24,25,30
2. Molar ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 delivers globular ionoids with almost perfect spherical shape. Based on the circular frame inside the IED (no change in time), we can conclude that these self-assembled entities exhibit high stability over the represented time-frame. Furthermore, we somewhat arbitrarily set the border globular ionoids to anisotropic ionic clusters at eccentricity 0.25 and a diameter of 25 nm or higher.
3 delivers globular ionoids with almost perfect spherical shape. Based on the circular frame inside the IED (no change in time), we can conclude that these self-assembled entities exhibit high stability over the represented time-frame. Furthermore, we somewhat arbitrarily set the border globular ionoids to anisotropic ionic clusters at eccentricity 0.25 and a diameter of 25 nm or higher.
3. Molar ratios 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 2
2, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 5
3 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 form long-lived anisotropic ionic clusters. These systems with a higher amount of 14+ compared to the established 1
6 form long-lived anisotropic ionic clusters. These systems with a higher amount of 14+ compared to the established 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-mixture6,7 do not reach their low eccentricity values, indicating adjustable shapes of our self-assembled entities due to tuning the ionic ratio of 14+ and 22−.
3-mixture6,7 do not reach their low eccentricity values, indicating adjustable shapes of our self-assembled entities due to tuning the ionic ratio of 14+ and 22−.
4. Molar ratios 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 show larger (weakly scattering) initial ionic structures that decompose into more trivial ion pair coordinations between 14+ and 22−, with the system at a 1
6 show larger (weakly scattering) initial ionic structures that decompose into more trivial ion pair coordinations between 14+ and 22−, with the system at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio having an inherently more anisotropic shape.
1 ratio having an inherently more anisotropic shape.
4 Conclusions
The ionic self-assembly process of the ‘Texas-sized molecular box’ (14+) with the small dianionic salts 22− and 32− into globular ionoids depends significantly on the molar ratio of the respective components. For the system 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− (14+
22− (14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32−, respectively), we detect highly defined, colloid-like structures with long-term stability6,7 at molar ratios from 1
32−, respectively), we detect highly defined, colloid-like structures with long-term stability6,7 at molar ratios from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 to 5
3 to 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6, which lead to ionic ratios between 2/3 and 5/3. Note that with changing the molar ratio of these instrinsically polyphilic molecules between 1
6, which lead to ionic ratios between 2/3 and 5/3. Note that with changing the molar ratio of these instrinsically polyphilic molecules between 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 5
3 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6, (i) the hydrodynamic radius of the ionic structures slightly shifts from 6 nm to 12 nm and (ii) the value of the eccentricity parameter is rising. The modified interplay between long-range electrostatic correlations and weaker noncovalent interactions indicates the possibility of adjusting the size and shape of our colloid-like structures by tuning the molar ratio of 14+ and 22− (32−, respectively).
6, (i) the hydrodynamic radius of the ionic structures slightly shifts from 6 nm to 12 nm and (ii) the value of the eccentricity parameter is rising. The modified interplay between long-range electrostatic correlations and weaker noncovalent interactions indicates the possibility of adjusting the size and shape of our colloid-like structures by tuning the molar ratio of 14+ and 22− (32−, respectively).
The CW EPR spectra demonstrate that with increasing concentration of 14+, while keeping the amount of the 32− ion constant, a slowed-down rotational mobility of Fremy's salt as well as an increasing line width due to stronger electrostatic interactions occurs. These effects could be measured in the initial ion cloud state at X- and Q-band frequencies, indicating their appearance both globally and in the local environment. In general, this can be interpreted as Fremy's salt being trapped in the charge sphere of one 14+, leading to stoichiometric ion pairs and thus the formation of loosely bound ion paired structures, as shown in the DLS data. However, at this point, it is not possible to quantify the contribution of electrostatic interactions to the total self-assembly process compared to weaker noncovalent forces.
Based on the introduced ionoid evolution diagram (IED), we are able to illustrate the ionic ratio influence on the formation of our highly defined structures (i) directly after the incubation time of ten days and (ii) throughout the entire measurement period. Furthermore, we can analyze the durability of the self-assembled ionic clusters as well as characterize their deviations from a spherical shape with the calculated eccentricity. Due to the studied molar ratios, we are able to define requirements for globular ionoids in the 14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22− (14+
22− (14+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32−, respectively) system, which comprise a diameter between 10 nm and 25 nm and an eccentricity lower than 0.25. Note that the constructed IED is only valid for the applied solvent mixture DMSO
32−, respectively) system, which comprise a diameter between 10 nm and 25 nm and an eccentricity lower than 0.25. Note that the constructed IED is only valid for the applied solvent mixture DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol
glycerol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 50
water 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v/v). In the long run, we want to compare the formation of our highly defined structures in various solvent mixtures using IEDs to understand the influence of, e.g., the dielectric constant or viscosity on the ionic self-assembly process and to simplify the required solvent mixture regarding possible applications in soft matter and supramolecular chemistry.
7 (v/v/v). In the long run, we want to compare the formation of our highly defined structures in various solvent mixtures using IEDs to understand the influence of, e.g., the dielectric constant or viscosity on the ionic self-assembly process and to simplify the required solvent mixture regarding possible applications in soft matter and supramolecular chemistry.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Till Hauenschild for synthesizing the 14+ compound and Dr. Andreas Kerth for helpful discussions (both MLU Halle-Wittenberg). We also gratefully acknowledge Heike Schimm and Stefanie Weber for continuing technical support. This work was financially supported by the Fonds der Chemischen Industrie (FCI).Notes and references
- Soft-Matter Characterization, ed. R. Borsali and R. Pecora, Springer, 2008 Search PubMed.
- R. Kimmich, Principles of Soft-Matter Dynamics – Basic Theories, Non-invasive Methods, Mesoscopic Aspects, Springer, 2012 Search PubMed.
- I. W. Hamley, Introduction to Soft Matter – Synthetic and Biological Self-Assembling Materials, John Wiley and Sons, Ltd, 2007 Search PubMed.
- I. W. Hamley and V. Castelletto, Angew. Chem., Int. Ed., 2007, 46, 4442–4455 CrossRef CAS PubMed.
- Nanoscale Assembly – Chemical Techniques, ed. W. T. S. Huck, Springer, 2005 Search PubMed.
- D. Kurzbach, D. R. Kattnig, N. Pfaffenberger, W. Schärtl and D. Hinderberger, ChemistryOpen, 2012, 1, 211–214 CrossRef CAS PubMed.
- J. Eisermann, L. Prager and D. Hinderberger, Phys. Chem. Chem. Phys., 2018, 20, 1421–1430 RSC.
- C. F. J. Faul, Acc. Chem. Res., 2014, 47, 3428–3438 CrossRef CAS PubMed.
- J.-M. Lehn, Science, 2002, 295, 2400–2403 CrossRef CAS PubMed.
- J.-M. Lehn, Proc. Natl. Acad. Sci. U. S. A., 2002, 8, 4763–4768 CrossRef PubMed.
- B. Rybtchinski, ACS Nano, 2011, 5, 6791–6818 CrossRef CAS PubMed.
- C. F. J. Faul and M. Antonietti, Adv. Mater., 2003, 15, 673–683 CrossRef CAS.
- Y. Haketa and H. Maeda, Chem. Commun., 2017, 53, 2894–2909 RSC.
- H.-Y. Gong, B. M. Rambo, E. Karnas, V. M. Lynch, K. M. Keller and J. L. Sessler, J. Am. Chem. Soc., 2011, 133, 1526–1533 CrossRef CAS PubMed.
- B. M. Rambo, H.-Y. Gong, M. Oh and J. L. Sessler, Acc. Chem. Res., 2012, 45, 1390–1401 CrossRef CAS PubMed.
- H.-Y. Gong, B. M. Rambo, V. M. Lynch, K. Kelly and J. L. Sessler, J. Am. Chem. Soc., 2013, 135, 6330–6337 CrossRef CAS PubMed.
- W. Schärtl, Light Scattering from Polymer Solution and Nanoparticle Dispersions, Springer, 2007 Search PubMed.
- J. Holoubek, J. Quant. Spectrosc. Radiat. Transfer, 2007, 106, 104–121 CrossRef CAS.
- A. P. Minton, Anal. Biochem., 2016, 501, 4–22 CrossRef CAS PubMed.
- R. Pecora, J. Nanopart. Res., 2000, 2, 123–131 CrossRef CAS.
- S. Bhattacharjee, J. Controlled Release, 2016, 235, 337–351 CrossRef CAS PubMed.
- S. K. Brar and M. Verma, TrAC, Trends Anal. Chem., 2011, 30, 4–17 CrossRef CAS.
- G. Jeschke, Macromol. Rapid Commun., 2002, 23, 227–246 CrossRef CAS.
- D. Hinderberger, G. Jeschke and H. W. Spiess, Macromolecules, 2002, 35, 9698–9706 CrossRef CAS.
- D. Hinderberger, H. W. Spiess and G. Jeschke, J. Phys. Chem. B, 2004, 108, 3698–3704 CrossRef CAS.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- D. Hinderberger and G. Jeschke, in Site-specific Characterization of Structure and Dynamics of Complex Materials by EPR Spin Probes, ed. G. A. Webb, Springer, 2006, ch. Characterization of Structure and Dynamics of Complex Materials, pp. 1529–1537 Search PubMed.
- A. W. A. Pauldrach, Das dunkle Universum – Der Wettstreit Dunkler Materie und Dunkler Energie: Ist das Universum zum Sterben geboren?, Springer, Spektrum, 2015 Search PubMed.
- W. Demtröder, Experimentalphysik 2 – Elektrizität und Optik, Springer, Spektrum, 2013 Search PubMed.
- D. Hinderberger, H. W. Spiess and G. Jeschke, Appl. Magn. Reson., 2010, 37, 657–683 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Containing information about the construction of our IEDs as well as details on analyzing DLS and CW EPR data. Furthermore, additional autocorrelation functions and CW EPR spectra as explained in the main text. See DOI: 10.1039/c8cp06558f |
| ‡ Hertzsprung–Russell diagrams are textbook knowledge in astrophysics, see e.g. Adalbert W. A. Pauldrach ‘Das dunkle Universium’,28 which in fact inspired us. |
| § Parameters a and b are the length of the semi-major and semi-minor axes of the ellipses. The exact adaptation of the eccentricity for the IEDs utilizing our DLS data can be found in the ESI.† |
| This journal is © the Owner Societies 2019 |