When hydrogen bonding overcomes Coulomb repulsion: from kinetic to thermodynamic stability of cationic dimers†
Abstract
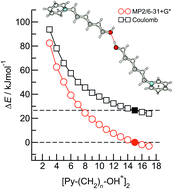
Quantum chemical calculations have been employed to study the kinetic and thermodynamic stability of hydroxy-functionalized 1-(3-hydroxyalkyl)pyridinium cationic dimers. For [Py–(CH2)n–OH+]2 structures with n = 2–17 we have calculated the robust local minima with clear dissociation barriers preventing their “Coulomb explosion” into separated cations. For n = 15 hydrogen bonding and dispersion forces fully compensate for the repulsive Coulomb forces between the cations allowing for the quantification of the pure hydrogen bond in the order of 20 kJ mol−1. The increasing kinetic stability even turns to thermodynamic stability with further elongated hydroxyalkyl chains. Now, quantum-type short-range attraction wins over classical long-range electrostatic repulsion resulting in negative binding energies and providing the first thermodynamically stable cationic dimers. The electronic, structural and spectroscopic signatures of the cationic dimers could be correlated to NBO parameters, supporting the existence of anti-electrostatic hydrogen bonds (AEHB) as recently suggested by Weinhold. In principle, these pure cationic dimers should be detectable in gas-phase experiments at low temperatures without the need of mediating molecules or counteranions.
- This article is part of the themed collection: 2019 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...