Open Access Article
Open Access ArticleRadiative cooling of cationic carbon clusters, CN+, N = 8, 10, 13–16
F.-Q.
Chen
a,
N.
Kono
b,
R.
Suzuki
b,
T.
Furukawa
b,
H.
Tanuma
b,
P.
Ferrari
 c,
T.
Azuma
d,
J.
Matsumoto
e,
H.
Shiromaru
c,
T.
Azuma
d,
J.
Matsumoto
e,
H.
Shiromaru
 e,
V.
Zhaunerchyk
f and
K.
Hansen
e,
V.
Zhaunerchyk
f and
K.
Hansen
 *fg
*fg
aSchool of Materials Science and Engineering, Tianjin University, Tianjin 300350, China
bDepartment of Physics, Tokyo Metropolitan University, 1-1 Minamiosawa, Hachiouji-shi, Tokyo 192-0397, Japan
cLaboratory of Solid State Physics and Magnetism, KU Leuven, 3001 Leuven, Belgium
dAtomic, Molecular & Optical Physics Laboratory, RIKEN, 2-1, Hirosawa, Wako-shi, Saitama 351-0198, Japan
eDepartment of Chemistry, Tokyo Metropolitan University, 1-1 Minamiosawa, Hachiouji-shi, Tokyo 192-0397, Japan
fDepartment of Physics, University of Gothenburg, 41296 Gothenburg, Sweden
gCenter for Joint Quantum Studies and Department of Physics, Tianjin University, Tianjin 300350, China. E-mail: KlavsHansen@tju.edu.cn
First published on 21st December 2018
Abstract
The radiative cooling of highly excited carbon cluster cations of sizes N = 8, 10, 13–16 has been studied in an electrostatic storage ring. The cooling rate constants vary with cluster size from a maximum at N = 8 of 2.6 × 104 s−1 and a minimum at N = 13 of 4.4 × 103 s−1. The high rates indicate that photon emission takes place from electronically excited ions, providing a strong stabilizing cooling of the molecules.
I. Introduction
The stability of molecules and clusters against unimolecular decomposition plays an important role in the dynamics and the chemical composition of any gas or plasma at low densities. When collision frequencies become comparable to and smaller than reciprocal dissociation times of excited species, all collisions that form molecules will, by energy conservation, create them with enough excess energy to ultimately cause dissociation, unless the excess energy is dissipated through other non-collisional channels.Radiative cooling provides one such dissipation channel. The amount of energy that must be carried away by photons to provide absolute stabilization of a collision complex is on the order of the thermal energy of the molecules before formation of the compound. At the same time the internal excitation energy is never less than the formation energy, which is often fairly large compared with thermal energies, implying that only a small fraction of the total energy of the complex needs to be removed to stabilize it. For molecules formed by reactions between smaller molecules and/or atoms with absent or essentially frozen vibrational motion, the energy necessary to quench dissociation is on the order of Boltzmann's constant times the ambient temperature, an energy that can be dissipated by emission of a single photon of an electronic transition or possibly even by a vibrational transition.
The molecular-specific radiative quenching rate therefore becomes an important factor in determining the survival probability of any molecule formed in collisions.1 The situation is particularly extreme in astrophysical context, where collision frequencies can be less than nHz between the numerous different molecular species now known to exist in space.2 This environment also produces the still poorly understood infrared emission bands, often assigned to polycyclic aromatic hydrocarbon molecules,3 which is of obvious interest in the context of radiative cooling processes. Radiation may, for example, play an important role in stabilizing intermediate products in the chain of processes through the top-down mechanism suggested in ref. 4 to be responsible for interstellar C60 production. The increasing list of molecular species found in space,5,6 many of them either carbon based or with a carbon backbone that opens up the possibility for unrestricted molecular growth, makes the question about the molecular survival influenced by radiative cooling particularly relevant.
Of the possible photon emission processes, photons appearing from thermally populated electronic states, in processes known as recurrent fluorescence,7–9 will for some molecules be the most efficient energy dissipation. Compared to the alternative thermal radiation by vibrational transitions, recurrent fluorescence radiation rates are on one hand reduced by the equivalent of the Boltzmann factor which suppresses the population of the emitting state, but are on the other hand enhanced by an oscillator strength for photon emission from these states which is usually much higher than that of vibrational transitions. The balance between these two factors is tipped toward enhancement of photon emission from the low-lying electronic states. This will tend to make radicals, with their lower lying states, more likely to emit radiation with high rates, tending to reverse the fitness pattern for molecular survival which is based on considerations of the higher binding energies of closed shell molecules.
Several species have been established as recurrent fluorescence coolers, both fullerenes,10–14 smaller carbon clusters,15–18 carbon-based molecules,19–22 and metal23–26 and semiconductor27,28 clusters. Anionic carbon clusters and molecules tend to have radiative cooling times on the order of tens or hundred microseconds to milliseconds. The cooling of small pure carbon cluster cations is much less known. Only the fullerenes of sizes N = 48–70, 76 have been investigated.10,12 We report here a study of the radiative properties of cationic carbon clusters of sizes N = 8, 10, 13–16, produced in a high temperature cluster source and measured at the Tokyo Metropolitan University electrostatic storage ring (TMU E-ring).
II. Experimental procedure
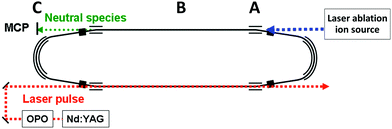
A schematic figure of the storage ring used is shown in Fig. 1. The clusters were produced in a laser ablation source with a 532 nm wavelength pulse from a YAG laser ablating a graphite surface. The ions, which were generated without gas cooling and therefore can be expected to be very highly excited vibrationally, were extracted by a pulsed field and further accelerated by a static electric field to a terminal kinetic energy of 15 keV, followed by an injection into the 7.736 m circumference storage ring29 where they circulated. At injection, a set of bending electrodes (at point A in Fig. 1) was briefly switched off to allow passage from the source line into the ring. After storage was accomplished, the cluster size of interest was selected by pulsing the deflection plates.The decays were measured time-resolved turn-by-turn in a neutral particle detector at point C at the end of the straight section (around point B in Fig. 1). The detector thus monitored the quasi-instantaneous decay rate of the stored species. The signal comprises all channels that emit neutral massive particles, irrespective of whether the emitted particles are atoms or molecules. Since radiative cooling quenches all non-radiative decays equally indiscriminately, the measured rates provide a faithful representation of the stabilizing effect of the radiation without the need to specify the decay channel. After measurements, the ions were dumped before a new bunch was injected.
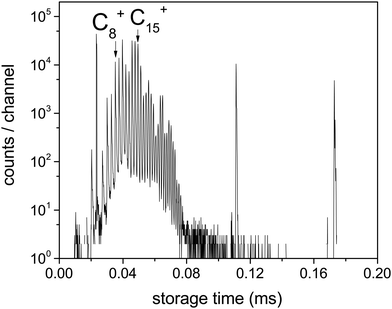
The laser was fired within 1 ms of injection. Fig. 2 shows the spontaneous decay spectrum for the first few turns in the ring, with mass selection of, in this case, the N = 15 cluster. The spectrum prior to mass selection represents decay rates that are shaped by the combined effects of ion abundances, dissociation energies, internal energy distributions, radiative cooling and possibly also stray counts from grazing collisions with the chamber walls. Because decay rates and not populations are measured here, a direct comparison of the spectrum in Fig. 2 with ion abundance spectra, even produced by similar methods, as in e.g.ref. 30, is therefore not possible.
Both spontaneous and laser induced decays were measured in the experiments. For the measurements of the photon induced decay, a 10 Hz tunable OPO laser was used to excite the clusters. The geometry gives measurements of the decay rates at times (n + 1/2)tc after the laser pulse, where 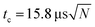 is the ion circulation time in the ring, and n is a non-negative integer. The number of ion injection/dumping cycles varied from 1.8 × 104 for the most intense beam of C15+ to above 2 × 105 for C10+. Fig. 3 shows examples of unimolecular decay spectra observed in the ring after mass selection of C15+ without and with a laser pulse. The laser power was monitored continuously. The highest pulse energy was 2.2 mJ per pulse, used at 520 nm on N = 15. Most of the wavelengths were chosen so the photon energies were high enough to cause a zero value of the t0 that appears in eqn (5), which was indeed found to be the case in the data analysis. This simplifies the data analysis but has no fundamental consequences. For N = 8 the choice was dictated by the photon absorption cross section. For N = 15, different wavelengths were used for the purpose of checking that the width of the excitation energy distribution was sufficiently broad to accommodate the special features used in the data analysis below.
is the ion circulation time in the ring, and n is a non-negative integer. The number of ion injection/dumping cycles varied from 1.8 × 104 for the most intense beam of C15+ to above 2 × 105 for C10+. Fig. 3 shows examples of unimolecular decay spectra observed in the ring after mass selection of C15+ without and with a laser pulse. The laser power was monitored continuously. The highest pulse energy was 2.2 mJ per pulse, used at 520 nm on N = 15. Most of the wavelengths were chosen so the photon energies were high enough to cause a zero value of the t0 that appears in eqn (5), which was indeed found to be the case in the data analysis. This simplifies the data analysis but has no fundamental consequences. For N = 8 the choice was dictated by the photon absorption cross section. For N = 15, different wavelengths were used for the purpose of checking that the width of the excitation energy distribution was sufficiently broad to accommodate the special features used in the data analysis below.
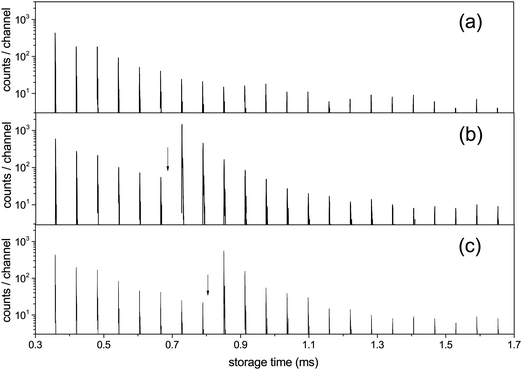 | ||
| Fig. 3 The C15+ spectrum (a) without laser excitation, (b) with photon energy 2.58 eV (λ = 480 nm) fired at times 0.682 ms, with the first enhanced ion signal detected at 0.729 ms, and (c) hν = 2.00 eV (λ = 620 nm) with the laser fired at 0.805 ms and the first enhanced peak appearing at 0.851 ms. Laser firing times are indicated by the vertical arrows. The laser is fired in one straight section of the ring and the neutral decay products are detected in the other, which causes one half turn delay between the laser pulse and the detected signal. An additional small delay, about a quarter of a period, in the detection is introduced by the travel time from the decay section to the detector (B to C in Fig. 1). | ||
III. Experimental results
For all clusters both the laser induced decays and the spontaneous decays of the hot clusters produced in the source were used to extract the cooling times. The photon energies used were hν = 2.38 eV (λ = 520 nm) for N = 10, 13, 14, 15, 16, hν = 2.58 eV (λ = 480 nm) for N = 15, hν = 2.00 eV (λ = 620 nm) for N = 15, and hν = 1.98 eV (λ = 625 nm) for N = 8. For N = 15, all of pulse energies, photon energies and laser firing times were varied. All the measured photon enhanced decay profiles were found to be identical, in the sense that the time dependence of the enhanced decay did not change with these parameters. This indicates that the enhanced signal is not shaped by source conditions but reflects intrinsic properties of the clusters. Furthermore, if the observed decay of the enhanced signal would be governed by the unimolecular rate constant, it should depend on the laser light wavelength and on the internal energies before excitation, effectively the storage time before laser excitation. However, this is seen experimentally not to be the case, and the disappearance of the signal after laser excitation cannot therefore be ascribed to the energy dependence of the rate constant ka. These conclusions agree with those drawn from previous experiments with the same apparatus on cooling of anions,14,31–33 and with a number of similar studies from other experimental facilities, see for example ref. 12, 13, 21, 22, 24, 26 and 34–37. Finally, as will be clear below, conclusions about the cooling rates do not depend on the precise number of photons absorbed, although we expect that most of the signal is due to single photon absorption.For all photon-induced decay, the enhanced decays were calculated from the data by subtraction of a reference laser-off spectrum, normalized to identical pre-laser counts to compensate for the (minor) fluctuations in the source intensity. The source has previously been tested in detail for stability with respect to the decay time profile of C60−, and it was found that although intensities could vary, the time profile of the signal had a very stable shape.14 This is consistent with the behavior observed here in the reference spectra and was assumed in the analysis. Examples of an integrated spectrum with and without laser enhancement is shown in Fig. 4.
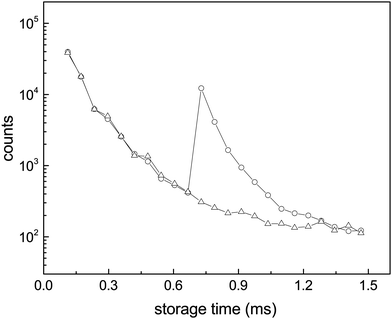 | ||
| Fig. 4 Enhanced decays of the N = 15 cluster after photon absorption. The data points are the integrals of the peaks in the spectra (a and b) of Fig. 3. The wiggles seen most clearly before the laser pulse are caused by the so-called betatron oscillations. The depletion of the number of the stored ions by laser irradiation is not discernible. | ||
Special consideration was paid in the analysis of the peak intensities to the possibility that the clusters could contain one or several hydrogen atoms, because hydrogen addition can change the radiative properties dramatically.15 The geometry of the laser overlap did not allow selective excitation of molecules differing in mass by 1 u, but the detected peaks are separated to a degree that it is possible to integrate intensities of ions differing by 1 u separately. Cooling times were found to be identical for the observable peaks corresponding to all-12C clusters and those 1 u higher. These higher mass clusters can therefore be assigned to clusters containing one 13C atom, and any presence of hydrogenated species is small enough to not affect the measured values.
IV. Analysis
In the absence of an external cooling gas in the source, the laser ablation produces clusters with broad excitation energy distributions. The highest excitation energies are sufficient to cause spontaneous unimolecular decay of the clusters in the storage ring, and most likely also during transfer from the source to the ring, although this is not directly observable. Decay from such an ensemble occurs as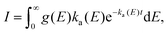 | (1) |
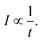 | (2) |
The presence of a power law decay rate, vs. the naively expected exponential decay, is essential for the observation of the radiative quenching, as was already noted in ref. 10 and 38. Radiative cooling will cause a deviation from this 1/t profile by reintroducing an exponential suppression of the decay at long times.34 For a few examples of previous applications of the technique, please see ref. 12–14 and 39 for fullerene studies, and ref. 19–22 for studies of carbon-based molecules.
The precise interpretation of such a radiatively quenched decay depends on the energy of the emitted photons. To reduce the unimolecular decay by the factor exp(1) or more, the photon energies need to exceed the value determined by
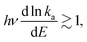 | (3) |
Proceeding with the one-photon radiative quenching of the unimolecular decays, the decay rates are to a good approximation given by33
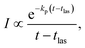 | (4) |
In addition to the quenching by radiative cooling, deviations from a pure power law after photo-excitation could also be caused by a photon energy that is too small to shift the energy distributions sufficiently high in energy to cause a 1/t decay.14 Such a situation will give a decay with a shifted zero time, t0 (see ref. 14 for an application, and the theoretical justification in ref. 41)
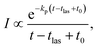 | (5) |
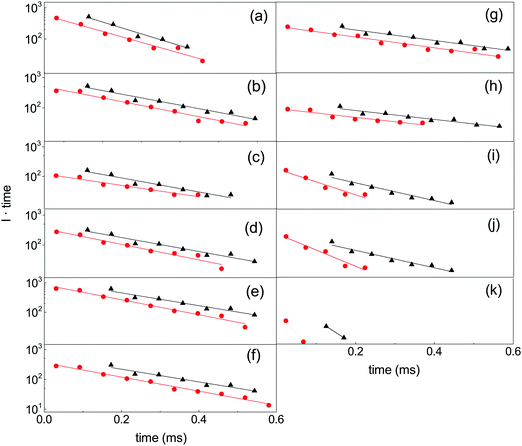
The suppression of the decay by radiative cooling is conveniently extracted by plotting the product of the enhanced count rate and the time elapsed after the photon absorption as a function of time after the photon absorption, as (t − tlas)I(t − tlas) ∝ exp(−kp(t − tlas)) vs. t − tlas for the laser based decays, and as tI(t) ∝ exp(−kpt) vs. t for the spontaneous decay. Fig. 5 shows this plot for all measured clusters sizes for both the laser enhanced peaks and the spontaneous decay from the source.
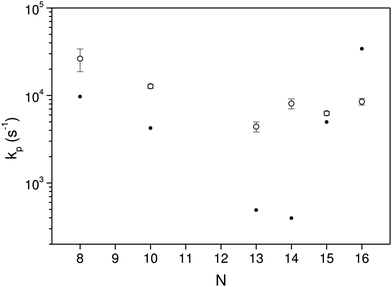
The curves are well fitted by an exponentially decreasing function, from which the photon emission rate constants kp are extracted directly. The good fits, which seem only to suffer from the betatron oscillations, confirm very convincingly the basis of analysis, viz. the presence of broad energy distributions and the concomitant power-law decay suppressed by radiative cooling. The values extracted from the source-produced decay and the photon enhanced signal are also in good agreement for N = 13, 14, 15, 16. Some difference between the two is seen for N = 10 and a more pronounced difference for N = 8, where slightly less than a factor of two separates the two. The differences for N = 8, 10 may be ascribed to the presence of high energy emitting states. Such states will be more sensitive to the excitation energy (temperature) than states at lower energies. Their presence cannot be confirmed from these data alone, but the quantum chemical calculations explained below do in fact give the two highest photon energy threshold for precisely N = 8 and N = 10 (0.95 eV and 0.60 eV, respectively). Although the spontaneous and light-induced rate constants for these two cluster sizes differ, we note that the variation is relatively small compared to the size dependence of the rate constants and we will use an average in the following. The values of kp are shown in Fig. 6. The five measured values of the spontaneous and the light-induced decay for N = 15 gave averages of (4.6 ± 0.3) × 103 s−1 for the spontaneous decay and (6.6 ± 0.2) × 103 s−1 for the light-induced decay. The errors given are those of the mean values.
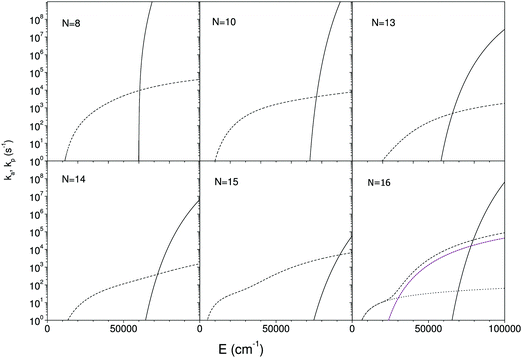
Since the radiative and unimolecular decay processes occur in parallel in the measurements, the measured radiative time constants correspond to the energy where the unimolecular decay constant, ka,N, and the radiative time constant are on the same order (see also Fig. 7);
| kp(E) ∼ ka,N(E). | (6) |
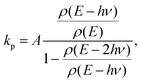 | (7) |
As is clear from the argument of the numerator in the expression, the photon emission rate constant represents a (microcanonically) thermally activated process. In principle this energy dependence of the photon emission process should be included into the calculation of the time profile that leads to eqn (4). The variation with excitation energy is, however, slow when compared with the unimolecular rate constant and it can be ignored without any major loss of precision. Appendix II shows this by an explicit calculation of the first order contribution of a finite slope of the photon emission vs. cluster excitation energy.
The observed photon emission rate constants include contributions from all possibly excited states and from both linear and ring conformers. The theoretical rate constants were calculated as the average over all emitting states, with energies hνi and spontaneous emission rate constants Ai-coefficients
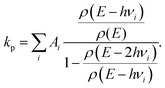 | (8) |
The relevant optical properties have not been measured. The spectra in ref. 43 do include the C8+, but only at much higher energies than relevant here. To find the quantities that enter this equation, a series of density functional theory (DFT) calculations were therefore performed. The vibrational quantum energies were calculated using the wB97X-D3 exchange–correlation functional and the Def2-SVP basis set, as implemented in the ORCA 4.0.1 software package.44 The properties of the electronically excited states were calculated by time-dependent DFT (TDDFT) using the same level of theory. All the electrons of carbon were included in the calculations. In addition, dissociation energies of all possible fragmentation channels were calculated. The applied level of theory was tested by its prediction of the correct lowest-energy isomer for each cluster size,45 as well as by the calculated dissociation channels. Vibrational frequencies were computed for all sizes and conformers, which were used to calculate level densities. The vibrational analysis was performed with the M062X functional and cc-pVTZ basis set from the Gaussian 16 package.46 For calculations of linear clusters, molecular symmetry constraints were implemented in order to obtain the correct number 3N − 5 of vibrational modes. Finally, also the energies and oscillator strengths of the three lowest excited states were calculated.
All cluster sizes calculated, N = 8 to 16, are rings in their lowest energy state. For N = 8, 9 the linear isomer ground state energy is between 0.8 eV and 0.9 eV above the ground state ring energy, whereas for the larger clusters the gap exceeds 2.1 eV, reaching 3.4 eV for C16+. These values are, apart from N = 10, consistent with ion mobility experiments,47 which observed the co-existence of rings and linear structures up to N = 10 and rings exclusively for larger cationic clusters. In that experiment the clusters are formed hot but quenched with a cooling gas, which may open the possibility that the structures are not sampled from entirely equilibrated thermal distributions. This will distort the comparison with the values calculated here. The lowest energies of the three optically active states calculated were 0.95 eV for N = 8; 0.60 eV for N = 10; 0.46 eV for N = 13; 0.46 eV for N = 14; 0.19 eV for N = 15; 0.18 eV for N = 16. All of these are therefore within reach of thermal excitation.
The lowest energy channels are in all cases the loss of a neutral carbon trimer:
| CN+ → CN−3+ + C3. | (9) |
The rate constants for these are calculated with the detailed balance equation42
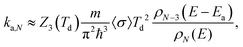 | (10) |
The calculated rate constants and photon emission rate are shown in Fig. 7. Only the radiation from the ring structures are included in the radiative rate constants, which are the sums of the three lowest optically excited states. The linear structures have generally significantly higher oscillator strengths than the ring structures, and the inclusion of radiation from linear structures will for most of the clusters give an extremely poor agreement with the experimental data.
V. Discussion
The radiative cooling of hot cationic carbon cluster observed in this work proceeds with very high rate constants that are only consistent with emission from thermally excited electronic states. The quantum mechanical calculations of the oscillator strengths and energies of such states do not agree well with the data, yielding emission rate constants that range more than two orders of magnitude from the lowest to the highest, whereas the experimental data cover less than an order of magnitude around 104 s−1. As such the theory can not be said to reproduce the experimental results.We do note, however, that the theoretical results bracket the experimental, with values both above and below the experimentally measured. We also note that any reasonable agreement requires that the linear conformers are excluded from the calculation of the optical rate constants, in spite of the fact that these states are not the lowest conformers, and that the opening of a ring requires an activation energy, in addition to the energy needed to excite the ion to the emitting electronic states. This leads to a strongly reduced population, but not sufficient to compensate for the much higher oscillator strength of these doubly excited states.
The exclusion of the linear conformers is entirely ad hoc and we can only speculate why this exclusion is necessary to obtain a semblance of agreement between theory and experiment. One possibility is that strong geometric deformations caused by the very highly excited vibrational states could push electronically excited state energies up and/or reduce thermally averaged oscillator strengths. In hot source productions the temperatures of the decaying clusters are determined by the dominant decay channel activation energies. In the present case the calculated values range between 5.89 and 8.54 eV. This gives (equivalent, or microcanonical) temperatures of the decaying ions often exceeding 4000 K, opening the possibility of exploring vastly larger parts of the phase space than the two conformers observed at low temperatures.
The theory-experiment deviations do not seem to correlate simply with the magnitude of the dissociation energy, but there is indeed a weak correlation between measured values of kp and calculated dissociation energies, with a tenfold increase in kp from D13 = 5.89 eV to D10 = 8.54 eV.
VI. Conclusion
The radiative rate constants of the carbon cations CN+, N = 8, 10, 13–16 have been measured and all found to be consistent with recurrent fluorescence, i.e. emission of radiation from thermally excited electronic states. The rate constants were all within a factor of three of 104 s−1, in contrast to the much more disperse values based on theoretically calculated energies and oscillator strengths.Conflicts of interest
There are no conflicts to declare.Appendix I
The rotational partition function that enters the unimolecular decay constant in eqn (10) is calculated with the high temperature limit of a non-linear molecule: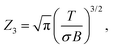 | (11) |
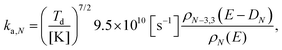 | (12) |
The level densities required for the rate constants were calculated with the Beyer–Swinehart algorithm60 with a numerical resolution of 1 cm−1, which was found sufficient. The temperature factor in eqn (12) was derived as an integral involving the logarithmic derivative of the level density. An expression which is both more precise and numerically convenient, in spite of its unwieldy appearance, is the sum
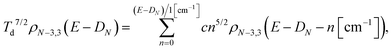 | (13) |
Appendix II
The expression for the measured decay rate with a constant photon emission rate constant is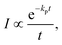 | (14) |
To do so, consider the derivation of eqn (14). It results from the ensemble averaging
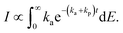 | (15) |
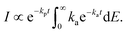 | (16) |
For an energy dependent kp we can then find the generalized expression by inserting the relevant energy dependent value of kp into eqn (14);
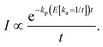 | (17) |
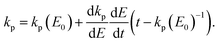 | (18) |
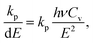 | (19) |
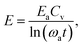 | (20) |
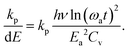 | (21) |
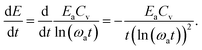 | (22) |
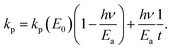 | (23) |
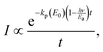 | (24) |
Acknowledgements
PF acknowledges the FWO for a post-doctoral grant. TA acknowledges the JSPS KAKENHI grant numbers 26220607. Calculations were performed at the Chalmers Centre for Computational Science and Engineering (C3SE) provided by the Swedish National Infrastructure for Computing (SNIC).References
- J. Zhen, S. Rodriguez Castillo, C. Joblin, G. Mulas, H. Sabbah, A. Giuliani, L. Nahon, S. Martin, J. P. Champeaux and P. M. Mayer, Astrophys. J., 2016, 822, 113 CrossRef PubMed.
- A. G. G. M. Tielens, Rev. Mod. Phys., 2013, 85, 1021 CrossRef CAS.
- H. Á. Galué and G. D. Leines, Phys. Rev. Lett., 2017, 119, 171102 CrossRef PubMed.
- O. Berné and A. G. G. M. Tielens, PNAS, 2012, 109, 402 CrossRef PubMed.
- J. Cami, J. Bernard-Salas, E. Peeters and S. E. Malek, Science, 2010, 329, 1180 CrossRef CAS PubMed.
- J. K. Jørgensen, C. Favre, S. E. Bisschop, T. L. Bourke, E. F. van Dishoeck and M. Schmalzl, Astrophys. J., Lett., 2012, 757, L4 CrossRef.
- A. Nitzan and J. Jortner, J. Chem. Phys., 1979, 71, 3524 CrossRef CAS.
- S. Leach, in Polycyclic Aromatic Hydrocarbons and Astrophysics, ed. A. Léger, L. d'Hendecourt and N. Boccara, NATO ASI Series, 1987, vol. 191, pp. 99–127, ISBN 978-94-010-8619-6 Search PubMed.
- A. Léger, P. Boissel and L. d'Hendecourt, Phys. Rev. Lett., 1988, 60, 921 CrossRef PubMed.
- K. Hansen and E. E. B. Campbell, J. Chem. Phys., 1996, 104, 5012 CrossRef CAS.
- J. U. Andersen, C. Brink, P. Hvelplund, M. O. Larsson, B. B. Nielsen and H. Shen, Phys. Rev. Lett., 1996, 77, 3991 CrossRef CAS PubMed.
- S. Tomita, J. U. Andersen, C. Gottrup, P. Hvelplund and U. V. Pedersen, Phys. Rev. Lett., 2001, 87, 073401 CrossRef CAS PubMed.
- J. U. Andersen, C. Gottrup, K. Hansen, P. Hvelplund and M. O. Larsson, Eur. Phys. J. D, 2001, 17, 189 CrossRef CAS.
- A. E. K. Sundén, M. Goto, J. Matsumoto, H. Shiromaru, H. Tanuma, T. Azuma, J. U. Andersen, S. E. Canton and K. Hansen, Phys. Rev. Lett., 2009, 103, 143001 CrossRef PubMed.
- G. Ito, T. Furukawa, H. Tanuma, J. Matsumoto, H. Shiromaru, T. Majima, M. Goto, T. Azuma and K. Hansen, Phys. Rev. Lett., 2014, 112, 183001 CrossRef CAS PubMed.
- V. Chandrasekaran, B. Kafle, A. Prabhakaran, O. Heber, M. Rappaport, H. Rubinstein, D. Schwalm, Y. Toker and D. Zajfman, J. Phys. Chem. Lett., 2014, 5, 4078 CrossRef CAS PubMed.
- N. Kono, T. Furukawa, H. Tanuma, J. Matsumoto, H. Shiromaru, T. Azuma, K. Najafian, M. S. Pettersson, B. Dynefors and K. Hansen, Phys. Chem. Chem. Phys., 2015, 17, 24732 RSC.
- Y. Ebara, T. Furukawa, J. Matsumoto, H. Tanuma, T. Azuma, H. Shiromaru and K. Hansen, Phys. Rev. Lett., 2016, 117, 133004 CrossRef PubMed.
- S. Martin, J. Bernard, R. Brédy, B. Concina, C. Joblin, M. Ji, C. Ortéga and L. Chen, Phys. Rev. Lett., 2013, 110, 063003 CrossRef CAS PubMed.
- S. Martin, M. Ji, J. Bernard, R. Brédy, B. Concina, A. R. Allouche, C. Joblin, C. Ortega, G. Montagne and A. Cassimi, et al. , Phys. Rev. A: At., Mol., Opt. Phys., 2015, 92, 53425 CrossRef.
- M. Ji, J. Bernard, L. Chen, C. Ortéga, A. Joblin, C. Cassimi and S. Martin, J. Chem. Phys., 2017, 146, 44301 CrossRef CAS PubMed.
- J. Bernard, L. Chen, R. Brédy, M. Ji, C. Ortéga, J. Matsumoto and S. Martin, Nucl. Instrum. Methods Phys. Res., Sect. B, 2017, 408, 21 CrossRef CAS.
- C. Walther, G. Dietrich, W. Dostal, K. Hansen, S. Krückeberg, K. Lützenkirchen and L. Schweikhard, Phys. Rev. Lett., 1999, 83, 3816 CrossRef CAS.
- M. Lange, M. W. Froese, S. Menk, D. Bing, F. Fellenberger, M. Grieser, F. Laux, D. A. Orlov, R. Repnow and T. Sieber, et al. , New J. Phys., 2012, 14, 065007 CrossRef.
- K. Hansen, Y. Li, V. Kaydashev and E. Janssens, J. Chem. Phys., 2014, 141, 024302 CrossRef PubMed.
- K. Hansen, M. H. Stockett, M. Kamińska, R. F. Nascimento, E. K. Anderson, M. Gatchell, K. C. Chartkunchand, G. Eklund, H. Zettergren and H. T. Schmidt, et al. , Phys. Rev. A, 2017, 95, 022511 CrossRef.
- P. Ferrari, E. Janssens, P. Lievens and K. Hansen, J. Chem. Phys., 2015, 143, 224313 CrossRef PubMed.
- P. Ferrari, J. Vanbuel, K. Hansen, P. Lievens, E. Janssens and A. Fielicke, Phys. Rev. A, 2018, 98, 012501 CrossRef.
- S. Jinno, T. Takao, K. Hanada, M. Goto, K. Okuno, H. Tanuma, T. Azuma and H. Shiromaru, Nucl. Instrum. Methods Phys. Res., Sect. A, 2007, 572, 568 CrossRef CAS.
- C. H. Bae and S. M. Park, J. Chem. Phys., 2002, 117, 5347 CrossRef CAS.
- M. Goto, A. E. K. Sundén, H. Shiromaru, J. Matsumoto, H. Tanuma, T. Azuma and K. Hansen, J. Chem. Phys., 2013, 139, 054306 CrossRef CAS PubMed.
- K. Najafian, M. S. Pettersson, B. Dynefors, H. Shiromaru, J. Matsumoto, H. Tanuma, T. Furukawa, T. Azuma and K. Hansen, J. Chem. Phys., 2014, 140, 104311 CrossRef CAS PubMed.
- N. Kono, T. Furukawa, H. Tanuma, J. Matsumoto, H. Shiromaru, T. Azuma, K. Najafian, M. S. Pettersson, B. Dynefors and K. Hansen, Phys. Chem. Chem. Phys., 2015, 17, 24732 RSC.
- K. Hansen, J. U. Andersen, P. Hvelplund, S. P. Møller, U. V. Pedersen and V. V. Petrunin, Phys. Rev. Lett., 2001, 87, 123401 CrossRef CAS PubMed.
- J. Fedor, K. Hansen, J. U. Andersen and P. Hvelplund, Phys. Rev. Lett., 2005, 94, 113201 CrossRef CAS PubMed.
- M. W. Froese, K. Blaum, F. Fellenberger, M. Grieser, M. Lange, F. Laux, S. Menk, D. A. Orlov, R. Repnow and T. Sieber, et al. , Phys. Rev. A: At., Mol., Opt. Phys., 2011, 83, 023202 CrossRef.
- C. Breitenfeldt, K. Blaum, M. Froese, S. George, G. Guzmá-Ramírez, M. Lange, S. Menk, L. Schweikhard and A. Wolf, Phys. Rev. A, 2016, 94, 033407 CrossRef.
- J. U. Andersen, C. Brink, P. Hvelplund, M. O. Larsson, B. B. Nielsen and H. Shen, Phys. Rev. Lett., 1996, 77, 3991 CrossRef CAS PubMed.
- J. U. Andersen, E. Bonderup and K. Hansen, J. Phys. B: At. Mol. Phys., 2002, 35, R1 CAS.
- R. C. Dunbar, Mass Spectrom. Rev., 1992, 11, 309 CrossRef CAS.
- K. Hansen, Int. J. Mass Spectrom., 2018, 430, 14 CrossRef CAS.
- K. Hansen, Statistical Physics of Nanoparticles in the Gas Phase, Springer Series on Atomic, Optical, and Plasma Physics, Springer, Dordrecht, 2nd edn, 2018, vol. 73 Search PubMed.
- J. Fulara, I. Shnitko, A. Batalov and J. P. Maier, J. Chem. Phys., 2005, 123, 044305 CrossRef PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73 CAS.
- G. von Helden, M. T. Hsu, N. Gotts and M. T. Bowers, J. Phys. Chem., 1993, 97, 8182 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson and H. Nakatsuji, et al., Gaussian 16, Revision b.01, 2016, Gaussian Inc., Wallingford, CT, 2016 Search PubMed.
- G. von Helden, P. R. Kemper, N. G. Gotts and M. T. Bowers, Science, 1993, 259, 1300 CrossRef CAS PubMed.
- M. E. Geusic, T. J. Mcllrath, M. F. Jarrold, L. A. Bloomfield, R. R. Freeman and W. L. Brown, J. Chem. Phys., 1986, 84, 2421 CrossRef CAS.
- M. E. Geusic, M. F. Jarrold, T. J. McIlrath, R. R. Freeman and W. L. Brown, J. Chem. Phys., 1987, 86, 3862 CrossRef CAS.
- P. P. Radi, M. E. Rincon, M. T. Hsu, J. Brodbelt-Lustig, P. Kemper and M. T. Bowers, J. Chem. Phys., 1989, 93, 6187 CrossRef CAS.
- M. B. Sowa, P. A. Hinz and S. L. Anderson, J. Chem. Phys., 1991, 95, 4719 CrossRef CAS.
- C. Lifshitz, P. Sandler, H. F. Griitzmacher, J. Sun, T. Weiske and H. Schwartz, J. Phys. Chem., 1993, 97, 6592 CrossRef CAS.
- R. Bouyer, F. R. Monchicourt, M. Perdix and P. Pradel, J. Chem. Phys., 1994, 100, 8912 CrossRef CAS.
- K. B. Shelimov, J. M. Hunter and M. F. Jarrold, Int. J. Mass Spectrom. Ion Processes, 1994, 138, 17 CrossRef CAS.
- A. Sinha and J. L. Kinsey, J. Chem. Phys., 1984, 80, 2029 CrossRef CAS.
- R. Wörgötter, B. Dünser, T. D. Märk, M. Foltin, C. E. Klots, J. Laskin and C. Lifshitz, J. Chem. Phys., 1996, 104, 1225 CrossRef.
- C. Lifshitz, Int. J. Mass Spectrom., 2000, 198, 1 CrossRef CAS.
- J. Laskin and C. Lifshitz, J. Mass Spectrom., 2001, 36, 459 CrossRef CAS PubMed ISSN 1096-9888.
- K. Hansen, E. E. B. Campbell and O. Echt, Int. J. Mass Spectrom., 2006, 252, 79 CrossRef CAS.
- T. Beyer and D. F. Swinehart, Commun. ACM, 1973, 16, 379 CrossRef , ISSN 0001-0782.
| This journal is © the Owner Societies 2019 |