Dynamics of benzene excimer formation from the parallel-displaced dimer†
Abstract
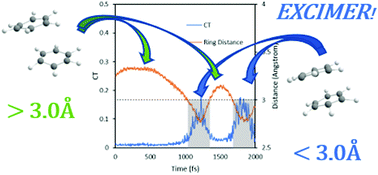
Excimers play a key role in a variety of excited-state processes, such as exciton trapping, fluorescence quenching, and singlet-fission. The dynamics of benzene excimer formation in the first 2 ps after S1 excitation from the parallel-displaced geometry of the benzene dimer is reported here. It was simulated via nonadiabatic surface-hopping dynamics using the second-order algebraic diagrammatic construction (ADC(2)). After excitation, the benzene rings take ∼0.5–1.0 ps to approach each other in a parallel-stacked structure of the S1 minimum and stay in the excimer region for ∼0.1–0.4 ps before leaving due to excess vibrational energy. The S1–S2 gap widens considerably while the rings visit the excimer region in the potential energy surface. Our work provides detailed insight into correlations between nuclear and electronic structure in the excimer and shows that decreased ring distance goes along with enhanced charge transfer and that fast exciton transfer happens between the rings, leading to the equal probability of finding the exciton in each ring after around 1.0 ps.
- This article is part of the themed collections: Celebrating Latin American Talent in Chemistry, Photodissociation and reaction dynamics and 2018 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...