Suppressing depolarization by tail substitution in an organic supramolecular ferroelectric

Abstract

Despite being very well established in the field of electro-optics, ferroelectric liquid crystals so far lacked interest from a ferroelectric device perspective due to a typically high operating temperature, a modest remnant polarization and/or poor polarization retention. Here, we experimentally demonstrate how simple structural modification of a prototypical ferroelectric liquid-crystal benzene-1,3,5-trisamide (BTA) – introduction of branched-tail substituents – results in materials with a wide operating temperature range and a data retention time of more than 10 years in thin-film solution-processed capacitor devices at room temperature. The observed differences between linear- and branched-tail compounds are analyzed using density functional theory (DFT) and molecular dynamics (MD) simulations. We conclude that morphological factors like improved packing quality and reduced disorder, rather than electrostatic interactions or intra/inter-columnar steric hindrance, underlay the superior properties of the branched-tailed BTAs. Synergistic effects upon blending of compounds with branched and linear side-chains can be used to further improve the materials’ characteristics.

---

Introduction

With increasing demand for cheap, efficient, lightweight and flexible electronics, a matching memory technology is required. Ferroelectricity-based memory devices assure non-volatility and low energy consumption, while organic materials, potentially used for this purpose, guarantee easy processability, low cost and advantageous physical properties. The discovery of ferroelectricity in organic thiourea more than 70 years ago¹ encouraged scientists to pursue research on dipolar small-molecular^2,3 as well as polymer^4,5 materials with a remnant charge displacement. This has resulted in organic materials with remnant polarization closely approaching the values found for conventional inorganic ferroelectrics like PZT and BTO. For instance, molecular diisopropylamonium bromide (DIPAB⁶) reaches values as high as 230 mC m⁻². However, in many cases organic ferroelectrics require careful growth of single crystals, which limits their application potential.^7,8 Therefore solution-processable materials with good film-forming properties are preferred.

Well-known examples of this kind of organic ferroelectrics are copolymers of PVDF and PTrFE. With remnant polarization in range 60–120 mC m⁻² together with piezoelectric and pyroelectric coefficients of −20 to −40 pm V⁻¹ and −10 to −40 μC m⁻² K⁻¹, P(VDF-TrFE) has been broadly utilized to fabricate piezoelectric^9,10 and pyroelectric devices,¹¹ as well as non-volatile memories of diverse structures.^12–14 However, the material only offers a limited tunability due to structural constraints and cannot provide enough structural freedom to tune properties and introduce new functionality, which is desired by the fast-developing field of organic electronics. A recently discovered class of amide-based dipolar columnar discotic liquid crystals offers the intriguing opportunity to tune key ferroelectric parameters by side chain modification¹⁵ as well as to introduce semiconducting properties by changing the π-conjugated core.^16,17 Yet, despite having a great potential for various applications, ferroelectric liquid crystals lacked interest from a ferro/piezo/pyroelectric device perspective due to typically high operating temperatures, modest remnant polarization and/or negligible polarization retention.^18–20

The archetypical amide-based liquid crystalline ferroelectric is trialkylbenzene-1,3,5-tricarboxamide (BTA), see Fig. 1. It is a C₃ symmetry discotic molecule with a benzene core, to which three amide groups, having a dipole moment of around 3 Debye each, are attached. These amides form intermolecular N⋯H–O hydrogen bonds that induce molecular self-assembly into columns with a triple-helix H-bonded network. Microdipoles within this system add up to a net axial macrodipole in a cooperative manner.²¹ When flexible mesogenic peripheral tails are attached, BTA enters a well-ordered liquid-crystalline columnar hexagonal phase, which facilitates rotation of the macrodipole and thus ferroelectric behavior.²² The π–π stacking of the benzene cores and packing of the tails further stabilize the molecular arrangement, which allows for unhampered dipole-flipping. Fitié et al. have discovered²⁰ and Gorbunov et al. have proven the true ferroelectricity of BTA material with linear alkyl chains in solution-processed capacitor devices.²³

Fig. 1 Primary, secondary and tertiary structure of the benzene-1,3,5-tricarboxamide (BTA) molecule. Self-assembly of the dipolar disk-shaped BTA molecules into columns with the axial macrodipole and consequent columnar-hexagonal packing leads to ferroelectric bistability and remnant polarization.

It is well known that properties of liquid crystals depend strongly on the peripheral tails attached.²⁴ Even though tail-substitution is an uncomplicated structural modification and the assortment of the tails is virtually unlimited, the choice of the tail-substituent for successful ferroelectric activity has certain constraints. First, mesogenic tails determine phase transition temperatures,²⁵ and since room temperature operation is strongly preferred from the application perspective, peripheral tails that assure the ferroelectricity-friendly liquid-crystalline phase being close to room temperature are of interest. Typically, very short tails result in purely crystalline materials,²⁶ while long bulky aliphatic tails are assumed to worsen long-range order and weaken intercolumnar coupling.²⁷ As both these extremities hinder collective dipolar switching, an optimum is sought after. We have recently shown that in fact all the key characteristics of the ferroelectric – remnant polarization, coercive field, polarization retention time and the operating temperature range – increase continuously in BTAs with shortening of the alkyl chain length from C₁₈H₃₇ to C₆H₁₃.¹⁵ The optimal hexyl-tailed BTA-C6 material demonstrated performance close to that of the P(VDF-TrFE): remnant polarization of ∼60 mC m⁻², fast polarization switching, low fatigue and polarization retention of several months at room temperature. This improvement was suggested to originate from tighter columnar packing and thus increased dipole density, accompanied by higher packing order and, presumably, strengthened electrostatic interactions.

All the experimental studies on ferroelectricity of BTAs reported so far have been based on molecules with linear alkyl chains attached.^19,20,23 Branched-tailed BTA homologues have been extensively researched by the groups of Meijer and Palmans with a focus on supramolecular polymerization in solution and its chiroptical activity.^28–30 Based on their findings, branched (chiral) tails bring more cooperativity, and thus promote formation of larger supramolecular structures, which improves the quality of the self-assembly in solution, compared to the linear-tailed analogues.³¹ Studies on the branched BTAs in the solid-state and their ferroelectric behavior have not been carried out. Yet it has been argued that branched side-chains may have impact on ferroelectric macrodipole ordering itself. Comparing compact and bulkier branched-tailed BTA molecules, Zehe et al. have argued that for domains with spontaneous polarization to form (i.e. ferroelectricity), substantial steric interactions among hexagonally packed dipolar columns must be present.²² This suggests that the ferroelectric state could be induced and stabilized with the help of tail-governed collective packing effects.

Motivated by the potential improvements in self-assembly and little-known impact of steric effects on polarization switching processes, we have synthesized and characterized BTAs having medium-length branched alkyl tails for this study. We expected tail branching to introduce extra steric hindrance at the intra- and inter-molecular level, which could improve the ferroelectric properties. To minimize the differences in electrostatics, we have chosen branched homologues with dipole density matching the already examined linear compounds. To refute the impact of chiral purity, racemic mixtures with random branch direction have been studied. We test the materials in spin-coated thin-film metal/ferroelectric/metal capacitor devices. The results on branched-tailed materials are compared to their linear analogues. With the help of density functional theory (DFT) and molecular dynamics (MD) simulations, the observed differences are then analyzed from the perspective of electrostatic and steric interactions, in context of structural and energetic disorder as well as inherent morphological layer properties. In contrast to expectations, morphological effects like enhanced self-assembly instead of steric effects, are found to play the key role in determining the device characteristics. It is further disclosed how simple mixing of selected compounds can lead to enhanced temperature stability, decreased coercive field and de facto no depolarization in BTA ferroelectric devices.

Results and discussion

Materials

Two branched BTA homologues BTA-C6/2 and BTA-C7/6 were used for experiments (Fig. 2). The synthesis of the material BTA-C6/2 with three 2-ethylhexyl tails of random stereochemistry was reported in ref. 25. The material BTA-C7/6 with achiral 1-hexylheptyl tails was originally synthesized for this study (for synthesis details see ESI,† Section I). We compared the results of these materials with their linear analogues that have closely matching molecular packing parameters or have equal number of carbons in the longest chain: BTA-C6 (hexyl tail), BTA-C8 (octyl tail) and BTA-C12 (dodecyl tail).¹⁵

Fig. 2 Molecular structure and saturating ferroelectric hysteresis loops with increasing applied field of (a) BTA-C6/2 with P_r ≈ 35 mC m⁻² and (b) BTA-C7/6 with P_r ≈ 34 mC m⁻² at 75 °C, 25 Hz.

Phase diagram and peculiarities of molecular packing

Liquid-crystalline substances typically have three phases – crystalline (Cr), liquid-crystalline (LC) and isotropic (Iso) – that are determined by the mobility of mesogenic tails and the strength of intermolecular interactions (non-covalent bonds). It was shown previously that BTAs with linear sidechains demonstrate all three typical phases with phase transition temperatures strongly dependent on the tail substituent.^15,25 For linear BTAs C6, C8, C10, C12 and C18 the Cr–LC phase transition was observed at 38 °C, 7 °C, 3 °C, 15 °C and 54 °C, respectively (data obtained by Differential Scanning Calorimetry (DSC) upon cooling, see Fig. S1a and b and ESI† for details). In the liquid-crystalline state BTA molecules are known to form ordered supramolecular structures, consisting of disk-like molecules axially stacked into columns. While these molecular stacks pack in columnar-hexagonal manner in the whole liquid-crystalline range for C8–C18 (wide-angle X-ray scattering (WAXS) data for BTA-C12 given in Fig. S2f (ESI†) as an example, for others in ref. 15), C6 demonstrates higher level ordering in the 38–155 °C temperature range, which can be attributed to the plastic-crystalline phase with a likely quasi-hexagonal p2gg lattice¹⁹ (Fig. S2e, ESI†). Here, we show that a similar plastic-crystalline phase can be attributed to the swallow-tailed BTA-C7/6 below 120 °C (Fig. S2c and d, ESI†). Above this temperature the phase changes to the columnar-hexagonal, until the melting point at 236 °C, where the material turns into the isotropic liquid. No pure crystalline phase was found for BTA-C7/6 down to −50 °C.

The other examined branched homologue BTA-C6/2 does not enter the fully crystalline phase, either. The material self-assembles into the ColHex lattice just below the melting temperature ∼280 °C, yet changes to highly-ordered plastic-crystalline state already at 235 °C and remains such till room temperature, see Fig. S1a, c and S2b (ESI†). The multitude of Bragg peaks arises from comparatively high long- as well as short-range order. The effect of enhanced self-assembly was also observed as a lower gel-point (intense gelation at lower concentrations in solution) of the BTA-C6/2, compared to all other examined homologues. The clearing (isotropic) temperature being significantly higher for branched homologues – BTA-C7/6 with 235 °C and especially BTA-C6/2 with 280 °C – compared to the linear ones (with melting points around 200 °C), might be considered as another indication of stronger self-assembly, i.e. an increased length of supramolecular polymer chains, arising from a higher degree of cooperativity in the branched materials.³²

Despite being in the plastic-crystalline state, both BTA-C6/2 and C7/6 columns pack hexagonally, as indicated by the characteristic Bragg peak distance ratio . The intercolumnar distance a of branched materials was found to be larger than their linear analogues of equal longest chain (see Fig. S2a, ESI,† data for 80 °C): 1.55 nm vs. 1.73 nm for C6 and C6/2; ∼1.63 nm vs. 2.02 nm for C7 and C7/6, respectively. This increase in intercolumnar distance can be explained by reduced tail intercalation between the adjacent columns due to branching.²⁵ Comparing the intercolumnar distances on basis of the total number of carbon atoms in the tail, equivalent molecules have closely matching parameters: C6/2 and C8 with total 8 carbons have 1.73 nm and 1.72 nm, respectively; C6/7 and C13 with 13 carbons – 2.02 nm and ∼2.15 nm, respectively. The interdisc distance c within columns is the same for all materials c = 3.4 Å, as it is mostly determined by the benzene cores and the amide network.

The packing differences discussed above are also reflected in the morphology of the layer, as observed by AFM, see Fig. S13 (ESI†). Branched material layers, being plastic-crystalline, have small (hundreds of nanometers) randomly oriented features with densely packed crystallites that strongly resemble the morphology of the P(VDF-TrFE). In contrast, liquid-crystalline linear BTAs form several-micrometer long supramolecular structures with prominent well-developed self-assembled fibers.

P–E characteristics and saturated polarization

Spin-coated thin film metal/ferroelectric/metal capacitor devices were fabricated for all materials to study the ferroelectric properties. For device preparation details we refer to the ESI,† Section II. We started characterization by measuring ferroelectric P–E characteristics, which were obtained from a measured switching current response to a triangular voltage signal, integrated over time. A non-switching background current was subtracted (ESI,† Section III). The resulting hysteresis curves with inner loops for C6/2 and C7/6 devices were found to be of close-to-ideal form, as seen in Fig. 2. A clear polarization saturation with increasing voltage was observed, which helps refute any secondary ferroelectricity-unrelated effects like ionic contamination,³³ electrochemical reactions,³⁴etc. The remnant polarization value found was around 35 mC m⁻² and 34 mC m⁻² for C6/2 and C7/6, respectively. Knowing the molecular packing parameters and the strength of the molecular dipole moment we can estimate a geometrically expected saturation polarization value for an ideal columnar hexagonal lattice. Using a constant 12 Debye dipole moment per molecule (based on theoretical estimates²¹), the calculated polarization value for C7/6 is 34 mC m⁻², which matches the experimentally obtained value, while the 45 mC m⁻² calculated for C6/2 is slightly higher than the measured remnant polarization, which suggests that macrodipole alignment could potentially be improved. Indeed, in a 1 : 1 mixture with BTA-C8, see below, the remnant polarization of C6/2 becomes around 42 mC m⁻².

Coercive field

A temperature scan of the P–E hysteresis loops revealed that the saturated remnant polarization is virtually temperature independent (Fig. S3, ESI†) for both the branched- and linear-tailed materials. Yet the corresponding coercive field value depends linearly on temperature (with a negative inclination) and is noticeably higher for the former ones, see Fig. 3a. We previously showed on BTA-C6 that the slope of the E_c–T characteristic is material phase dependent and that it becomes steeper after entering the crystalline state.¹⁵ Based on DSC and WAXS measurements, no purely crystalline state could be found in the branched homologues, yet a sharp inclination of the dependence, similar to that of the linear BTA-C6 in the crystalline state (black symbols), is seen for the BTA-C7/6 material (red symbols) below 95 °C. Similarly to the BTA-C6 case, the material remains fully switchable below this temperature. However, above ∼95 °C BTA-C7/6 shows a second peak in the switching current transients and fast polarization relaxation, due to which no reliable coercive field value can be obtained (more details in the ESI,† Section V). Below ∼40–50 °C the coercive field of the BTA-C7/6 devices became higher than the breakdown field. BTA-C6/2 (blue symbols), being in a highly-ordered plastic-crystalline state below 235 °C, has a weaker T dependence than BTA-C7/6, similar to the linear BTAs in the LC phase. Due to that, BTA-C6/2 has a broader operating temperature range – from far above 100 °C down to room temperature and below. No unusual behavior was observed in BTA-C6/2 devices.

Fig. 3 (a) Temperature dependence of the coercive field for linear BTA-C6 (black symbols), BTA-C6/2 (blue symbols) and BTA-C7/6 (red symbols). Due to high-temperature tail-coupled effects explained in the text, the coercive field value of BTA-C7/6 above 95 °C is speculative. Data measured at 10 Hz applied field frequency. (b) Depolarization activation plot with data collected from multiple devices. Data are fitted to the Arrhenius equation (lines) with activation energy values given in the legend.

We have previously shown that polarization switching in BTAs is dispersive and proceeds through extensive nucleation, which restricts further monotonous growth of ferroelectric domains.^23,35 This kind of switching process is typical for polycrystalline, disordered ferroelectrics and can be described by so-called nucleation-limited switching (NLS) models.^36,37 With thermal activation included, the NLS model can successfully describe the temperature dependence of ferroelectric parameters.^38–40 The model states that, at a sufficiently high applied field, the ferroelectric switching process in nucleation-limited systems can be explained relating it to the thermally activated reversal of a critical domain of volume V* and characteristic activation energy density w_b. The coercive field E_c is then:

where ν₀ is the characteristic attempt frequency, t is the reciprocal field sweeping frequency, P_r is the remnant polarization, k_B is the Boltzmann constant and T is temperature. Eqn (1) correctly predicts the linear temperature-coercive field relation, the slope of which is determined by ∼ln(ν₀)/V*, while the intercept comes from the barrier energy density w_b. The w_b/P_r term gives the coercive field at 0 K, E_c0. The fitting parameters for a constant attempt frequency of 1 THz are given in Table S1 (ESI†).

Both the higher w_b (∼0.7 eV nm⁻³vs. ∼0.15 eV nm⁻³) and E_c0 (∼2000 V μm⁻¹vs. ∼400 V μm⁻¹) in the crystalline state of BTA-C6 compared to its LC state clearly indicates coupling between the switching process and the peripheral tail mobility. In view of that, the fact that the extracted parameters (Table S1, ESI†) are very similar for linear and branched homologues suggests that branched tail-induced steric hindrance might not have a very strong influence on the observed differences in the coercive field. We test this hypothesis by density functional theory and molecular dynamics simulations, vide infra.

To inspect whether the higher coercive field values of the branched material devices as compared to their linear analogues can alternatively be explained by stronger dipolar interactions or by higher remnant polarization, we plot the coercive field E_c values versus the intercolumnar packing distance of the materials (measured at T = 70 °C and f = 25 Hz), see Fig. S4a (ESI†). The coercive field of the branched C7/6 exceeds that of the linear BTA-C12 by ∼5 times (210 V μm⁻¹vs. 40 V μm⁻¹), despite having the same packing parameters. A similar though weaker effect is seen when comparing BTA-C6/2 and BTA-C8 (180 V μm⁻¹vs. 55 V μm⁻¹). These high coercive field values are close to the theoretical intrinsic coercive field. If considered as half the depolarization field⁴¹E_c ≈ 1/2E_d = 1/2P_r/ε_rε₀, the intrinsic value for both branched materials would be around 400 V μm⁻¹ for a constant relative permittivity ε_r = 5 (from the displacement-field characteristics after full poling) and P_r ≈ 35 mC m⁻². Alternatively, based on the Landau–Devonshire theory for second-order phase transitions⁴² with the free energy given by G = G₀ + 1/2αP² + 1/4βP⁴ − PE, the intrinsic coercive field becomes . This gives a coercive field of ∼150 V μm⁻¹ for branched and ∼110–240 V μm⁻¹ for linear C18–C6 (see Fig. S4a, ESI,† asterisks). Clearly, differences in the intrinsic coercive field cannot explain the experimentally observed tail-branching related trends, as it is solely polarization dependent. This implies that the increase in the coercive field upon introduction of branched tails results from other than electrostatic effects, like steric hindrance, layer morphology and disorder.

Polarization retention and switching time

We measured the polarization retention by fully poling the device and probing the lost (back-switched, relaxed) polarization part after a certain waiting time during which the devices were left at short-circuit conditions.²⁷ Measurements are performed at elevated temperatures to accelerate the thermally activated depolarization process and move the depolarization constants towards the measurable timescales. The measurement results at different temperature are given in Fig. 4. The depolarization kinetics data fits well to a characteristic stretched exponential function ∼exp[−(t/τ)^β] with β = 0.5, where t is the waiting time and τ the depolarization time constant.²⁷ Practically no deviations from this trend have been found in BTAs,^15,27 which allows for reliable prediction of the depolarization kinetics at unpractical timescales and different temperatures. The well-expressed Arrhenius-type depolarization activation allows for further extrapolation to lower temperatures with high precision.

Fig. 4 (a) Depolarization kinetics of BTA-C6/2 with BTA-C6, C8 and C12 for comparison at 80 °C (grey shades, open circles), and (b) BTA-C7/6, showing suppressed depolarization below 80 °C. Dotted lines in panel (a) correspond to the same measurement temperature. Data fitted to a stretched exponent function with β = 0.5 with an exception of BTA-C7/6 due to fast relaxation >80 °C and plateau-like depolarization trends <80 °C.

It is apparent that polarization decays several orders of magnitude faster in linear BTAs C12, C8 and C6 (grey shades, open circles in Fig. 4a) than in their branched homologues, despite closely matching macrodipole packing. Comparing the data for 80 °C, the depolarization time constant increases from ∼35 s, ∼125 s and ∼770 s for BTA-C12, C8 and C6, respectively, to ∼3.2 × 10⁶ s for BTA-C6/2 and over 10¹² s for BTA-C7/6 (extrapolated values). While for all other homologues the fitting parameter β is around 0.5 and the depolarization is accelerated by the thermal impact gradually, an unusual behavior is observed for the BTA-C7/6 material. As seen in Fig. 4b, below 80 °C the depolarization is significantly slowed down, resulting in stretched-exponential depolarization with β values under 0.1. Decreasing the temperature further to <70 °C reveals unusual plateau-like depolarization kinetics within the measured 10⁵ s range, which implies that depolarization in BTA-C7/6 is (partly) suppressed. A forced stretched-exponent fitting results in time constants far above the age of the Universe. In contrast to all other homologues, polarization in BTA-C7/6 is lost rapidly above 80 °C and almost immediately after exceeding 95 °C, which is related to excessive tail mobility as further discussed in the ESI† (Section V and Fig. S5). Here we focus on temperatures closer to room temperature at which BTA-C7/6 behaves as a regular ferroelectric.

The extracted depolarization time constants for all materials are plotted vs. temperature in Fig. 3b. Data for branched BTAs is marked in color and shows up to 5 orders of magnitude longer polarization retention, compared to their linear analogues (grey shades). Fitting the data to a simple Arrhenius equation gives depolarization activation energy E_a, which grows from ≈0.9–1.55 eV for linear C18–C6 BTAs to 1.75 eV for BTA-C6/2. The attempt frequency decreases by ∼10 times in going from BTA-C6 to BTA-C6/2, having close activation energies. The exceptionally steep dependence for BTA-C7/6 around the transitional 95 °C temperature, that would correspond to an 8.3 eV activation energy, is unlikely to originate from regular temperature activation of depolarization. For comparison, we have performed retention measurements on P(VDF-TrFE) (77–23%) devices at similar temperatures (black asterisks), which gives a slope of 5.3 eV and a time constant of the same order as BTA-C6/2 and BTA-C7/6: τ = 3 × 10⁶ s at 90 °C. Clearly, both BTA-C7/6 and P(VDF-TrFE) are close to their critical temperature points; the Curie temperature for P(VDF-TrFE)_77:23 is ∼140 °C.⁴³ No reliable activation energy could be obtained for BTA-C7/6 at lower temperatures due to the previously mentioned plateau-like depolarization trends. Yet it suggests that the effective barrier for depolarization becomes comparable or higher than the depolarization field and can no longer be overtaken thermally.

Turning to the kinetics under a driving field, we find that branched BTAs have an order of magnitude longer polarization switching time than their linear analogues as shown in Fig. S6a (ESI†). To enable comparison to simulation data presented below, we fit the high-field data to the classical empirical Merz law⁴⁵t_sw = t₀ exp(E₀/E). This gives the activation field E₀ = 170–210 V μm⁻¹ for linear BTAs C6–C12 and ∼300 and ∼420 V μm⁻¹ for C6/2 and C7/6, respectively (Fig. S6b, ESI†). The characteristic switching time t₀ ranges between 12–37 μs for C6–C12 and 150 and 60 μs for C6/2 and C7/6, respectively (Fig. S6c, ESI†). Note that BTA-C7/6 has a comparatively short t₀ due to the relatively high temperature 80 °C that was used. Clearly, both the activation field E₀ and the minimum switching time t₀ are larger for the branched homologues, which is consistent with the differences in depolarization behavior.

As for the differences in the coercive field discussed above, the higher depolarization activation energy, the longer retention and the slower switching of branched BTAs compared to linear BTAs having the same packing parameters, cannot be explained by increased dipolar interactions. This leaves us with intra- and intercolumnar steric interactions, layer morphology and disorder as possible determinant factors.

Molecular dynamics simulations

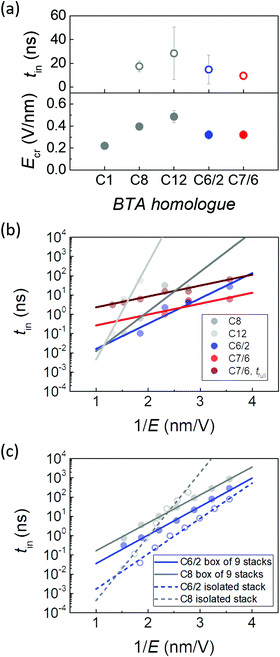
To further test the possible reasons for the remarkable improvement in data retention as well as the growth in the coercive field of branched BTA homologues, we performed a combination of DFT and MD simulations, see Section VI in the ESI† for details. DFT calculations were first performed on a model system of BTA-C1 with single methyl tails (Fig. S7, ESI†) to examine the behaviour of the possible rotamers for monomer and dimer species. MD simulations were performed on single stacks and boxes containing multiple stacks for BTAs having longer mesogenic tails, namely C8, C12, C6/2 and C7/6. Prior to the switching studies, we performed a series of simulations on boxes made of 9 stacks for C8, C12, C6/2, and C7/6 to study the effect of the substitutions on the packing. Initial boxes were relaxed in an NPT ensemble. Columnar hexagonal packing of molecular columns was found for all materials (Fig. S10, ESI†) and the intercolumnar distances obtained were in good agreement with the experimental X-ray scattering data, as summarized in Table S2 (ESI†).

Single stack switching

To study the polarization switching processes within a single isolated molecular stack, we performed simulations with different external electric field values and followed the changes of the H-bonded network. Calculated values for the switching initialization time, i.e. time required for the switching process to start, as a function of the applied electric field strength E are shown in Fig. 5 and Table S3 (ESI†).

Fig. 5 (a) Critical field E_cr and switching initialization time t_in at this field, calculated for single isolated stacks of different BTA homologues. (b) Switching initialization time dependence on the reciprocal applied field. Simulated data (symbols) is fitted to the Merz equation (lines). The full switching time t_full of an isolated stack for BTA-C7/6 is given in dark red and is substantially longer compared to other homologues with switching duration of ≤0.2 ns. (c) Comparison of averaged t_invs. E trends between BTA-C6/2 and BTA-C8 for isolated stacks (open symbols, dashed lines) and averaged characteristics over 9-stack boxes (full symbols, solid lines).

First, we compared BTAs with linear tails. Simulations showed that to initiate switching, we need significantly larger electric fields for longer substitutions. For C1, C8 and C12, we find ∼0.22 V nm⁻¹, ∼0.4 V nm⁻¹ and ∼0.5 V nm⁻¹, respectively (Fig. 5a). This indicates that this critical electric field strongly depends on the total mass of the tail and it is thus likely influenced by intracolumnar steric effects. The trend of increasing critical switching field with longer peripheral chain lengths is opposite to the experimentally observed one, where the experimental coercive field (equivalent to the simulated critical field) continuously reduces with tail-lengthening.¹⁵ Simulation results can be rationalized by higher stabilization energy of molecules with longer tails (−111 kcal mol⁻¹ for C12vs. −91 kcal mol⁻¹ for C8, Table S4, ESI†) due to increased van der Waals interactions, but the observed discrepancy with the experimental results suggests that a consideration of additional effects such as inter-columnar interactions is required.

For branched tails even stronger steric effects would be expected, especially for the tails with branching points closer to the BTA core. Surprisingly, in both branched homologues C6/2 and C7/6, switching started at an applied field of around 0.32 V nm⁻¹, which is slightly lower than the values obtained for linear BTAs. This is again in stark contrast to the experimentally observed trend, where the branched materials have a 3–5 times higher coercive field (Fig. S4a, ESI†). A similar discrepancy was observed in the switching time trends: an order of magnitude longer switching time was found for branched materials experimentally (Fig. S6a, ESI†), while simulation results indicate the contrary. At 0.43 V nm⁻¹ the average switching time for C8, C12, C6/2 and C7/6 were ∼22 ns, ∼28 ns, ∼1.2 ns and ∼5.5 ns, respectively.

Although no significant differences were observed between materials regarding the simulated switching initialization time and the critical field, exceptional behavior was noticed in the switching dynamics after initialization of C7/6. The duration of the switching event (Table S3, ESI†) did not exceed 0.2 ns for the other homologues, while for C7/6 the switching process stretched over 50 ns. This indicates that individual molecules in the C7/6 stack do not switch simultaneously. The field dependence of the switching time is also considerably weaker for C7/6, as seen in Fig. 5b.

The switching time shortening with increasing field fits well to the classical empirical Merz law⁴⁴t_sw = t₀ exp(E₀/E), see Fig. 5b. The extracted fitting parameters for different homologues are E₀ ≈ 7.5, 7, 4.3, 1.7 V nm⁻¹ and t₀ ≈ 0.0002, 0.01, 0.02, 64 ps for BTA-C8, C12, C6/2 and C7/6, respectively (Fig. S6d and e, ESI†). Fitting the full-switching data for C7/6 gives the same activation field and t₀ ≈ 435 ps. Besides its weaker field dependence, C7/6 is characterized by an almost two orders of magnitude longer t₀. In principle, the position of the branching point may play a role, as more steric hindrance for switching is expected for molecules where it sits closer to the amides. This would mainly increase the critical switching field. However, even though branching occurs at the very first carbon atom of the C7/6 tail, no notable increase in the critical or in the activation field is observed compared to C6/2 that has the branching point at the second carbon, or compared to the linear BTAs. Therefore, both the simulated low activation field and the unusually long switching process are suggested to result from the high structural disorder within stacks due to the bulky tails of C7/6.

The calculated critical field values are roughly an order of magnitude higher than those obtained experimentally. This is a consequence of the fact that simulations are necessarily performed at much shorter timescales (nanoseconds vs. milliseconds) and the coercive field is known to grow rapidly with decreasing probing time, cf. e.g. the Du–Chen⁴⁵ and Ishibashi–Orihara⁴⁶ models. In addition, while experimentally observed polarization switching is to be considered extrinsic, the simulated processes are still largely intrinsic. It is a well-known fact, often referred as the Landauer paradox, that intrinsic coercive fields are typically much larger than the experimentally observed ones. Focusing therefore on relative differences, the simulation results on single isolated molecular stacks at 300 K cannot explain the experimentally observed significant differences between branched and linear BTA homologues. In fact, opposite trends in critical field and switching initiation time are obtained. This implies that intermolecular steric hindrance within stacks can be disregarded as the effect governing the macroscopic (real-device experimental) polarization switching characteristics.

Box switching

To study the effect of intercolumnar interactions, we built boxes of 9 BTA stacks in 3 : 0 rotamer with all amides pointing the same direction for C8 and C6/2 (Fig. S9, ESI†). First, a more than 10% increase in total interaction energy per molecule was observed in boxes, compared to isolated molecular stacks, which was mainly caused by strengthened van der Waals interactions (Table S4, ESI†). Hence, steric effects are present between molecular stacks, stabilizing the system.²² This leads to higher critical switching fields in boxes than in single isolated stacks (Table S5, ESI†): ∼0.43 V nm⁻¹vs. ∼0.28–0.36 V nm⁻¹ for C6/2 and ∼0.54 V nm⁻¹vs. ∼0.36–0.43 V nm⁻¹ for C8. Interestingly, the calculated total energy per molecule (∼102 kcal mol⁻¹) is very similar to the activation energies obtained by dielectric relaxation spectroscopy (∼140 kcal mol⁻¹) on linear BTAs corresponding to the helicity change of the amide network (R-relaxation).¹⁹

The disorder within boxes leads to a distribution in critical fields and switching initiation times, see Table S5 and Fig. S11 (ESI†). The distribution of calculated critical fields, i.e. a projection of the Preisach distribution,⁴⁷ is of Gaussian form, which matches experimentally obtained results on linear BTAs from our previous work.³⁵ Being centered around the same ∼0.35 V nm⁻¹ value, this distribution is narrower for BTA-C6/2 compared to C8, which indicates lower disorder in the box of the former compound. This may be the underlying reason for the faster switching and higher activation field in C6/2, as seen from comparison of averaged switching characteristics over 9-stacks in Fig. 5c (full symbols, solid lines): E₀ ≈ 3.5 V nm⁻¹, t₀ ≈ 1.2 ps and E₀ ≈ 3.2 V nm⁻¹, t₀ ≈ 12 ps from fits to the Merz equation for C6/2 and C8, respectively. Compared to single isolated stacks (E₀ ≈ 3 V nm⁻¹, t₀ ≈ 0.78 ps for C6/2 and E₀ ≈ 4.7 V nm⁻¹, t₀ ≈ 0.11 ps for C8, open symbols and dashed lines), polarization switching in boxes proceeds slightly slower for both materials, which can again be attributed to inter-columnar steric effects. These factors influence the total stack switching speed as well: it took on average 0.6 ns for all molecules within an individual stack in a box to switch (Table S5, ESI†), while in isolated stacks full switching occurred almost immediately (<0.2 ns) with the noted exception of BTA-C7/6.

Based on the simulation results on both isolated single stacks and 9-stack boxes, it is evident that intercolumnar interactions stabilize the system, leading to higher critical fields for switching initiation and longer times for switching to start and to complete at that field. Structural disorder leads to slower switching process, which is especially significant for C7/6. This confirms our previously suggested reasoning for faster polarization switching in shorter-substituted, and less disordered, linear BTAs.¹⁵ However, neither the experimentally observed exceptional polarization stabilization (long retention) in branched homologues, nor the high coercive field and longer switching time can be directly explained by intra- and intercolumnar steric and electrostatic interactions in BTAs. Although our DFT/MD simulations were performed at a constant 300 K, it is unlikely that increased temperature effects on, for instance, the tail mobility (e.g. crystallization or melting) would lead to the experimentally observed systematic differences. Therefore, alternative influences must be considered. As we simulate intrinsic microscopic effects, macroscopic extrinsic properties of real ferroelectric layers, such as layer morphology (e.g. stack size and level of disorder) and domain-related characteristics (domain size and evolution) cannot be studied. We suggest it is these two types of effects that are dominant in actual macroscopic devices.

While strong manifestations of structural disorder were observed in the switching behavior of simulated stacks and boxes of branched molecules (especially the swallow-tailed C7/6), the experimentally obtained opposite trends suggested that, macroscopically, branched materials’ layers possess higher order, compared to the linear homologues. As mentioned before, it is known that, due to a higher degree of cooperativity, branched chiral molecules tend to form higher quality self-assemblies,³¹ which also holds for their mixtures with linear homologues.^48,49 Even though our branched homologues are not enantiopure, enhanced self-assembly is still expected. Due to this, larger molecular self-assemblies are formed in the branched material layers, which leads to an increased volume and reduced number of the nucleation centers for polarization switching. As polarization switching in these materials is limited by nucleation, this reduces the possibility for polarization reversal both with and without the applied electric field, which consequently results in higher coercive fields and suppressed depolarization. The much stronger improvement in polarization retention (more than 5 orders of magnitude) compared to the increase in the coercive field (2–5 times) in the branched molecules’ devices can be explained by their different sensitivity to the decreased disorder. Cornelissen et al. have demonstrated by kinetic Monte-Carlo simulations that structural disorder has a much stronger impact on the depolarization rate than on the coercive field value.⁵⁰ Therefore, a lower level of structural and energetic disorder allows for significant improvement in polarization retention with only a slight increase in the concomitant coercive field value. These principles hold for blends of linear and branched BTAs, that are discussed further, as well.

Mixtures of linear and branched BTAs

As demonstrated above, branched BTAs offer exceptionally long polarization retention at the cost of a higher coercive field. With the intention of circumventing this trade-off, we prepared devices from mixtures of linear and branched molecules. We chose a 1 : 1 ratio to examine the effect of mixing branched and linear materials. The BTA-7/6 and BTA-C12 pair was chosen first due to matching packing parameters and the stable, yet moderate performance of BTA-C12.

Ferroelectric capacitor devices from a 1 : 1 ratio mixture of C12 with C7/6 were tested in the same way as discussed above. No double peak or other oddities were seen in the switching kinetics and the switching current transients of the mixed-material devices, so molecular segregation can be refuted, suggesting that branched and linear molecules stack into columns in more or less random order (Fig. S12d, ESI†). The absence of phase segregation was confirmed by the AFM topographies in Fig. S13 (ESI†) and DSC thermograms in Fig. S1a (ESI†). The isotropization temperature of BTA-C12:C7/6 blend shifted to ∼250 °C compared to ∼235 °C of BTA-C7/6 and ∼200 °C of BTA-C12, which indicates that a more stable phase than that of the individual compounds is formed. The measured P–E hysteresis loops demonstrated full saturation (Fig. S12a, ESI†) with a remnant polarization around 32 mC m⁻², which is likely determined by the molecule with the larger intercolumnar spacing of the two, BTA-C12. The polarization switching time and the coercive field of the mixed-material devices were found to sit in between those of the pure BTA-C7/6 and BTA-C12, see Fig. S4, S6a and S12e (ESI†). The mixed-material devices demonstrated weaker E_c temperature dependence and continued to switch normally far above 90 °C with a well-defined coercive field, which indicates that the previously discussed relaxation found in BTA-C7/6 above 90 °C was suppressed. As a result, the operating temperature range extended significantly, from below room temperature to over 140 °C.

Surprisingly, the polarization retention for the C12:C7/6 devices is several orders of magnitude longer compared to both the BTA-C12 and BTA-C7/6 at higher temperatures. At around 90 °C (Fig. 6a) the depolarization time constant τ grows from ∼10 s for the neat compounds to ∼10⁷ s, i.e. several months, for the blend. At temperature as high as 130 °C (dark red half-full symbols in Fig. 6a) the depolarization time constant is still ∼10⁶ s (around 10 days). Depolarization kinetics fit well to the stretched exponential function with β = 0.5 in the whole measured temperature range. The behavior below 80 °C becomes similar to the branched BTA-C7/6 (Fig. S4b, c and S12f, ESI†) – with no detectable depolarization within the measured 10⁵ s range and extrapolated polarization retention exceeding 10 years (>3.15 × 10⁸ s). We speculate that this synergistic effect is caused by delayed/suppressed melting of the branched C7/6 chains due to interaction with the linear C12. With this excessive tail mobility factor turned off, the C12:C7/6 mixture ‘inherits’ remarkable polarization stability from the BTA-C7/6, even at high temperature.

Fig. 6 Depolarization kinetics of linear (open symbols, dotted lines), branched (full symbols, solid lines) and mixed linear-branched (half-full symbols, dash-dotted lines) materials devices: (a) C12, C7/6, C12:C7/6 and (b) C8, C6/2, C8:C6/2, C12:C6/2, as indicated in the legend.

To confirm the hypothesis, we also tested a 1 : 1 mixture of BTA-C6/2, which has not demonstrated any abnormalities, and BTA-C12. Although resulting in well-behaved ferroelectric devices, the active layer formed by the C12:C6/2 mixture gave rise to parameters in between those of the constituent compounds, as seen in Fig. 6b (half-right symbols), Fig. S4, S6, S12b, e and f (ESI†). No synergy in retention was observed. This can be rationalized in terms of the apparent absence of any detrimental side effects that limit the retention of pure BTA-C6/2. A contributing factor to the absence of synergistic effects might be that the intercolumnar distance of BTA-C12 and BTA-C6/2 does not match (2.08 nm and 1.73 nm, respectively). To refute the effect of the packing mismatch, we tested a BTA-C8:C6/2 1 : 1 mixture. This allowed to reach higher remnant polarization values of around 42 mC m⁻², which is closer to the geometrically expected 45 mC m⁻² than that found for pure BTA-C6/2 (∼35 mC m⁻²). Likely, BTA-C8 reduces viscosity, therefore the field-alignment procedure used for pre-conditioning of our out-of-plane devices is more effective and a greater part of the molecular stacks are aligned homeotropically. However, all other characteristics of the BTA-C8:C6/2 mixture landed around halfway between the BTA-C6/2 and C8, yet they were better than for C12:C6/2, see Fig. 6b, Fig. S4, S6, S12c, e and f (ESI†).

Hence, we can conclude that indeed the suppressed side-chain melting due to intermixture of branched C7/6 and linear C12 chains is the key to the significantly improved polarization retention in the mixture of BTA-C7/6:C12 at higher temperatures. Our findings for BTA-C6/2:C12 and BTA-C6/2:C8 do, on the other hand, show that mixing of BTA homologues can be a straightforward way to achieve parameter values that are intermediate to the pure compounds. At a purely phenomenological level, this finding is consistent with the morphologies as visualized by AFM, see Fig. S13 (ESI†), that show highly ordered directional stacks for the mixtures with a characteristic length scale that is in between the pure linear and branched compounds. The 1 : 1 mixtures having middling characteristics prove that the improvement is linear and no amplification effects, previously demonstrated in diluted solutions of branched-chiral and linear-achiral BTAs mixtures,^50,51 are present in our random stereochemistry mixtures in the solid-state.

To recapitulate, the results on the linear-branched mixtures attest that the characteristics of the linear material can be improved by adding a branched homologue, and, at certain conditions, the other way around, due to enhanced self-assembly and induced tail–tail interactions. This leads to anomalous synergistic effects if strongly branched tails are mixed with long linear ones. A dramatic manifestation of that effect has been observed in BTA-C12:C7/6 mixtures as 6–8 orders of magnitude longer polarization retention at high temperatures compared to both components separately and no measurable depolarization at lower temperatures. In all cases, blending of linear and branched materials led to reduced coercive field values compared to the pure branched compounds, while the polarization stability was significantly improved compared to the linear homologues.

Conclusions

By means of flexible tail engineering – introduction of branched segments – and blending we were able to suppress depolarization in organic supramolecular ferroelectric BTA and achieve polarization retention in thin-film spin-coated capacitor devices that exceeds commercial memory requirements. Both examined branched homologues – swallow-tailed BTA-C7/6 (1-hexylheptyl tails) and BTA-C6/2 (2-ethylhexyl tails) – demonstrated stable ferroelectric switching with remnant polarization around 35–45 mC m⁻² and extrapolated polarization retention of more than 10¹² s at room temperature. The accompanying comparatively high coercive field of the branched materials (∼200 V μm⁻¹, 25 °C, 10 Hz) was lowered by mixing with linear analogues having matching packing parameters. The resulting achiral branched-linear BTA mixtures had shorter sub-millisecond polarization switching time and an operating temperature range from far above 140 °C to room temperature and below, which is broader than that of the popular organic ferroelectric P(VDF-TrFE). This is caused by unprecedented synergistic effects observed in BTA-C12:C7/6 blends that lead to strongly suppressed depolarization at and even far above room temperature. On the basis of experimental findings and detailed molecular dynamics simulations we argue that the underlying factors in this performance improvement are not the dipolar electrostatic interactions or intermolecular steric hindrance, but morphological effects like enhanced self-assembly, facilitated axial column growth and improved layer order. The findings may assist in the further rational advancement in the field of small-molecular liquid-crystalline ferroelectrics via molecular engineering.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

I. U. and P. N. acknowledge funding by Vetenskapsrådet. T. D. C. acknowledges financial support from the Swedish Government Strategic Research Area in Materials Science on Functional Materials at Linköping University (Faculty Grant SFO Mat LiU No. 2009 00971). M. L. thanks SeRC (Swedish e-Science Research Center) for funding. The Swedish National Infrastructure for Computing (SNIC) at National Supercomputer Centre (NSC) and Center for High Performance Computing (PDC) are acknowledged for providing computer resources.

References

1. A. L. Solomon, Thiourea, a New Ferroelectric, Phys. Rev., 1956, 104, 1191.
2. A. S. Tayi, A. Kaeser, M. Matsumoto, T. Aida and S. I. Stupp, Supramolecular ferroelectrics, Nat. Chem., 2015, 7, 281–294.
3. S. Horiuchi and Y. Tokura, Organic ferroelectrics, Nat. Mater., 2008, 7, 357–366.
4. M. Poulsen and S. Ducharme, Why ferroelectric polyvinylidene fluoride is special, IEEE Trans. Dielectr. Electr. Insul., 2010, 17, 1028–1035.
5. B. Z. Mei, J. I. Scheinbeim and B. A. Newman, The ferroelectric behavior of odd-numbered nylons, Ferroelectrics, 1993, 144, 51–60.
6. I. Bergenti, et al., Highly Ordered Organic Ferroelectric DIPAB-Patterned Thin Films, Langmuir, 2017, 33, 12859–12864.
7. S. Horiuchi, et al., Above-room-temperature ferroelectricity in a single-component molecular crystal, Nature, 2010, 463, 789–792.
8. A. S. Tayi, et al., Room-temperature ferroelectricity in supramolecular networks of charge-transfer complexes, Nature, 2012, 488, 485–489.
9. K. S. Ramadan, D. Sameoto and S. Evoy, A review of piezoelectric polymers as functional materials for electromechanical transducers, Smart Mater. Struct., 2014, 23, 33001.
10. S. B. Lang and S. Muensit, Review of some lesser-known applications of piezoelectric and pyroelectric polymers, Appl. Phys. A: Mater. Sci. Process., 2006, 85, 125–134.
11. D. Setiadi, P. P. L. Regtien and P. M. Sarro, Application of VDF/TrFE copolymer for pyroelectric image sensors, Sens. Actuators, A, 1994, 42, 585–592.
12. P. Heremans, et al., Polymer and Organic Nonvolatile Memory Devices, Chem. Mater., 2011, 23, 341–358.
13. B. B. Tian, et al., Tunnel electroresistance through organic ferroelectrics, Nat. Commun., 2016, 7, 11502.
14. V. Khikhlovskyi, et al., Nanoscale organic ferroelectric resistive switches, J. Phys. Chem. C, 2014, 118, 3305–3312.
15. I. Urbanaviciute, et al., Tuning the Ferroelectric Properties of Trialkylbenzene-1,3,5-tricarboxamide (BTA), Adv. Electron. Mater., 2017, 3, 1600530.
16. A. V. Gorbunov, et al., Ferroelectric self-assembled molecular materials showing both rectifying and switchable conductivity, Sci. Adv., 2017, 3, e1701017.
17. A. V. Gorbunov, et al., Switchable Charge Injection Barrier in an Organic Supramolecular Semiconductor, ACS Appl. Mater. Interfaces, 2016, 8, 15535–15542.
18. H. Takezoe and F. Araoka, Polar columnar liquid crystals, Liq. Cryst., 2014, 41, 393–401.
19. C. F. C. Fitié, et al., Polar switching in trialkylbenzene-1,3,5-tricarboxamides, J. Phys. Chem. B, 2012, 116, 3928–3937.
20. C. F. C. Fitié, W. S. C. Roelofs, M. Kemerink and R. P. Sijbesma, Remnant polarization in thin films from a columnar liquid crystal, J. Am. Chem. Soc., 2010, 132, 6892–6893.
21. C. Kulkarni, S. K. Reddy, S. J. George and S. Balasubramanian, Cooperativity in the stacking of benzene-1,3,5-tricarboxamide: the role of dispersion, Chem. Phys. Lett., 2011, 515, 226–230.
22. C. S. Zehe, et al., Mesoscale Polarization by Geometric Frustration in Columnar Supramolecular Crystals, Angew. Chem., Int. Ed., 2017, 56, 4432–4437.
23. A. V. Gorbunov, et al., True ferroelectric switching in thin films of trialkylbenzene-1,3,5-tricarboxamide (BTA), Phys. Chem. Chem. Phys., 2016, 18, 23663–23672.
24. T. Wöhrle, et al., Discotic Liquid Crystals, Chem. Rev., 2016, 116, 1139–1241.
25. A. Timme, R. Kress, R. Q. Albuquerque and H. W. Schmidt, Phase behavior and mesophase structures of 1,3,5-benzene- and 1,3,5-cyclohexanetricarboxamides: towards an understanding of the losing order at the transition into the isotropic phase, Chem. – Eur. J., 2012, 18, 8329–8339.
26. D. Kluge, et al., Influence of the Molecular Structure and Morphology of Self-Assembled 1,3,5-Benzenetrisamide Nanofibers on their Mechanical Properties, Small, 2012, 8, 2563–2570.
27. A. V. Gorbunov, et al., Polarization loss in the organic ferroelectric trialkylbenzene-1,3,5-tricarboxamide (BTA), Phys. Chem. Chem. Phys., 2017, 19, 3192–3200.
28. P. J. M. Stals, et al., Dynamic supramolecular polymers based on benzene-1,3,5-tricarboxamides: the influence of amide connectivity on aggregate stability and amplification of chirality, Chem. – Eur. J., 2010, 16, 810–821.
29. A. R. A. Palmans and E. W. Meijer, Amplification of chirality in dynamic supramolecular aggregates, Angew. Chem., Int. Ed., 2007, 46, 8948–8968.
30. M. M. J. Smulders, et al., Probing the Limits of the Majority-Rules Principle in a Dynamic Supramolecular Polymer, J. Am. Chem. Soc., 2010, 132, 620–626.
31. C. Kulkarni, E. W. Meijer and A. R. A. Palmans, Cooperativity Scale: A Structure-Mechanism Correlation in the Self-Assembly of Benzene-1,3,5-tricarboxamides, Acc. Chem. Res., 2017, 50, 1928–1936.
32. P. J. M. Stals, M. M. J. Smulders, R. Martín-Rapún, A. R. A. Palmans and E. W. Meijer, Asymmetrically substituted benzene-1,3,5-tricarboxamides: self-assembly and odd-even effects in the solid state and in dilute solution, Chem. – Eur. J., 2009, 15, 2071–2080.
33. T. Kato, et al., Transport of ions and electrons in nanostructured liquid crystals, Nat. Rev. Mater., 2017, 2, 17001.
34. X. Meng, et al., Ferroelectric switching and electrochemistry of pyrrole substituted trialkylbenzene-1,3,5-tricarboxamides, J. Polym. Sci., Part B: Polym. Phys., 2017, 55, 673–683.
35. I. Urbanaviciute, T. D. Cornelissen, X. Meng, R. P. Sijbesma and M. Kemerink, Physical reality of the Preisach model for organic ferroelectrics, Nat. Commun., 2018, 9, 4409.
36. A. K. Tagantsev, I. Stolichnov, N. Setter, J. S. Cross and M. Tsukada, Non-Kolmogorov-Avrami switching kinetics in ferroelectric thin films, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 1–6.
37. J. Y. Jo, et al., Domain Switching Kinetics in Disordered Ferroelectric Thin Films, Phys. Rev. Lett., 2007, 99, 267602.
38. M. Vopsaroiu, J. Blackburn, M. G. Cain and P. M. Weaver, Thermally activated switching kinetics in second-order phase transition ferroelectrics, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 24109.
39. M. Vopsaroiu, P. M. Weaver, M. G. Cain, M. J. Reece and K. B. Chong, Polarization Dynamics and Non-Equilibrium Switching Processes in Ferroelectrics, IEEE Trans. Ultrason., Ferroelectr., Freq. Control, 2011, 58, 1867–1873.
40. K. B. Chong, F. Guiu and M. J. Reece, Thermal activation of ferroelectric switching, J. Appl. Phys., 2008, 103, 14101.
41. V. M. Fridkin and S. Ducharme, General features of the intrinsic ferroelectric coercive field, Phys. Solid State, 2001, 43, 1320–1324.
42. S. Kim, V. Gopalan and A. Gruverman, Coercive fields in ferroelectrics: a case study in lithium niobate and lithium tantalate, Appl. Phys. Lett., 2002, 80, 2740–2742.
43. G. Teyssedre, A. Bernes and C. Lacabanne, Cooperative movements associated with the Curie transition in P(VDF-TrFE) copolymers, J. Polym. Sci., Part B: Polym. Phys., 1995, 33, 879–890.
44. W. J. Merz, Domain formation and domain wall motions in ferroelectric BaTiO₃ single crystals, Phys. Rev., 1954, 95, 690–698.
45. X. Du and I.-W. Chen, Frequency Spectra of Fatigue of PZT and other Ferroelectric Thin Films, MRS Proc., 1997, 493, 311.
46. H. Orihara, S. Hashimoto and Y. Ishibashi, A Theory of D-E Hysteresis Loop Based on the Avrami Model, J. Phys. Soc. Jpn., 1994, 63, 1031–1035.
47. F. Preisach, Über die magnetische Nachwirkung, Z. Phys., 1935, 94, 277–302.
48. M. M. J. Smulders, A. P. H. J. Schenning and E. W. Meijer, Insight into the mechanisms of cooperative self-assembly: the ‘sergeants-and-soldiers’ principle of chiral and achiral C₃-symmetrical discotic triamides, J. Am. Chem. Soc., 2008, 130, 606–611.
49. M. M. J. Smulders, et al., Tuning the extent of chiral amplification by temperature in a dynamic supramolecular polymer, J. Am. Chem. Soc., 2010, 132, 611–619.
50. T. D. Cornelissen, M. Biler, I. Urbanaviciute, M. Linares and M. Kemerink, Kinetic Monte Carlo simulations of organic ferroelectrics, Phys. Chem. Chem. Phys., 2018 10.1039/C8CP06716C.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp06315j

---