Non covalent interactions stabilizing the chiral dimer of CH2ClF: a rotational study†
Abstract
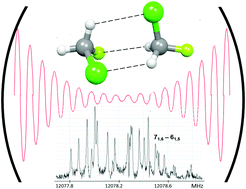
We report the rotational spectra of three isotopologues of the dimer of chlorofluoromethane, namely CH235ClF–CH235ClF, CH235ClF–CH237ClF and CH237ClF–CH235ClF. The assigned (most stable) conformer is chiral (C1 symmetry) and displays a network of two C–H⋯Cl–C and one C–H⋯F–C weak hydrogen bonds, combined with a Cl⋯F halogen bond. The hyperfine structures due to the quadrupolar effects of the two non-equivalent 35Cl (or 37Cl) atoms have been fully resolved, leading to an accurate determination of two sets of diagonal and of some mixed quadrupole coupling constants. Information on the rs positions of the two Cl atoms and on the structural parameters of the hydrogen bonds has been obtained. The dissociation energy of the complex has been estimated as 5.9 kJ mol−1.
- This article is part of the themed collection: Challenges in spectroscopy: accuracy vs interpretation from isolated molecules to condensed phases


 Please wait while we load your content...
Please wait while we load your content...