Quantitative analysis of ¹⁴N quadrupolar coupling using ¹H detected ¹⁴N solid-state NMR

Abstract

Magic-angle spinning solid-state NMR is increasingly utilized to study the naturally abundant, spin-1 nucleus ¹⁴N, providing insights into the structure and dynamics of biological and organic molecules. In particular, the characterisation of ¹⁴N sites using indirect detection has proven useful for complex molecules, where the ‘spy’ nucleus provides enhanced sensitivity and resolution. Here we exploit the sensitivity of proton detection, to indirectly characterise ¹⁴N sites using a moderate rf field to generate coherence between the ¹H and ¹⁴N at moderate and fast-magic-angle spinning frequencies. Efficient numerical simulations have been developed that have allowed us to quantitatively analyse the resulting ¹⁴N lineshapes to determine both the size and asymmetry of the quadrupolar interaction. Exploiting only naturally occurring abundant isotopes will aid the analysis of materials with the need to resort to isotope labelling, whilst providing additional insights into the structure and dynamics that the characterisation of the quadrupolar interaction affords.

---

Introduction

Nitrogen-14 has a natural abundance of >99.6% and a moderate gyromagnetic ratio (γ_¹⁴N/γ_¹H ∼ 0.07), making it a potentially attractive nucleus for high-resolution solid-state NMR studies of nitrogen containing compounds. However, ¹⁴N is a spin-1 nucleus with a nuclear quadrupole interaction (NQI) typically on the order of 1–5 MHz, making detection challenging. The NQI is however sensitive to variations in molecular symmetry, geometry and electrostatic environment, which in combination with its high natural abundance and prevalence in organic and biological materials, makes the development of methods to characterize ¹⁴N sites desirable. To this end, a number of methods have been presented in the literature, particularly within the last ten years, that facilitate the determination of NQI parameters of nitrogen sites in a range of organic, biological and pharmaceutical materials.

Despite the size of the NQI and the width of resulting signal, ultra-wideline excitation methods developed by Schurko and co-workers have provided accurate NQI parameters at ¹⁴N sites in a number of organic and pharmaceutical compounds.^1–3 The resolution of this method is inherently limited by the width of static ¹⁴N signals, which overlap and hinder interpretation, limiting this technique to compounds with few (currently fewer than 3) unique ¹⁴N sites.

Methods for detection of overtone (Δm = ±2) transitions on static samples,^4–6 and more recently under MAS^7–12 and DOR¹³ have provided alternative methods for characterizing ¹⁴N sites. Unlike Δm = ±1 ¹⁴N signals, overtone signals are not affected by the large (MHz) quadrupole broadening. However, there are sensitivity concerns when exciting this “forbidden” transition, which are further exacerbated by the slow nutation and correspondingly low excitation bandwidth of overtone signals, making simultaneous detection of multiple ¹⁴N overtone signals difficult.⁸

A third strategy for detection of ¹⁴N is the indirect detection method, pioneered independently by Gan and Bodenhausen's laboratories,^14–25 where ¹⁴N sites are detected via their interaction with coupled spin-1/2 ‘spy’ nuclei; typically ¹H or ¹³C, using pulse sequences qualitatively similar to HMQC experiments. Transfer of polarisation between the ¹⁴N and the ‘spy’ nucleus occurs due to high-order cross-terms between the quadrupolar and ¹⁴N‘spy’ dipolar Hamiltonians, known as the ‘residual dipolar splitting’ (RDS), as well as a contribution from the J-coupling, in experiments known as J-HMQCs. Alternatively, polarisation transfer can be driven by the recoupling of the ¹H/¹⁴N dipolar coupling using rotary resonance (R³), REDOR or symmetry based recoupling sequences, in sequences that have been generally termed D-HMQC experiments.^19,26,27 Similarly, double cross-polarization schemes have also been proposed for indirect detection which function well at higher spinning speeds.²⁸ These indirect techniques benefit from the sensitivity and resolution that are afforded by the ‘spy’ nuclei and do not require excitation or detection of the entire first-order broadened ¹⁴N spectrum. Accordingly, they have found application to the study of structure and dynamics of a number of systems.^18,29,30 One of the major obstacles to the more widespread application of these techniques is their relatively poor spy nucleus/¹⁴N transfer efficiencies, which usually result in a ∼90% drop in sensitivity compared to the ¹H spin-echo, and the strong dependency on high ¹⁴N RF amplitudes,³¹ this is particularly acute at moderate spinning speeds (<60 kHz). This, in turn, renders the accurate de novo determination of ¹⁴N NQI parameters from these experiments difficult, since precise determination of the quadrupolar coupling constant (C_Q) and asymmetry parameter (η) requires fitting of the ¹⁴N lineshape, which cannot be achieved without high quality spectra with a high S/N ratio.

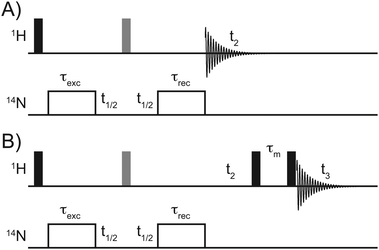
In this study we present a method for indirect detection of ¹⁴N signals via¹H's with enhanced efficiency at moderate to fast MAS frequencies (35–70 kHz), with transfer efficiencies of up to 27.5%, enabling acquisition of ¹H/¹⁴N correlation spectra with improved signal/noise ratios and well-defined lineshapes in the ¹⁴N dimension. This method, which is derived from our earlier work on the detection of ¹⁴N via¹³C,³² differs from previously published methods of indirect ¹⁴N detection based on the HMQC pulse sequence, in that polarisation transfer occurs not under free evolution or established methods of heteronuclear dipolar recoupling, but rather under relatively long (100s μs) periods of moderate (30–70 kHz) RF irradiation on the ¹⁴N channel (see Fig. 1). As described in our earlier studies, during these periods of irradiation both single and double quantum coherences are generated with efficiencies in excess of 20% of the initial equilibrium magnetization.³² As per previous indirect detection sequences the indirect ¹⁴N signals in 2D spectra are not affected by the typically large (MHz) first order quadrupolar interaction providing that the t₁ increments are rotor synchronised and the magic-angle accurately set. This results in ¹⁴N signals at a frequency which is the sum of the chemical shift and second order isotropic quadrupolar shift (δ^iso_Q), given for the general case in ppm by:²⁹

where I and m are the spin quantum numbers and υ₀ is the Larmor frequency in Hz. Eqn (1) simplifies to:In the case of ¹⁴N, when I = 1 and m = +1 or 0. The quadrupolar product, χ_q, is given by:If the isotropic chemical shift, δ^iso_CS, is known, for example from studies of ¹⁵N spectra, then the ¹⁴N δ^iso_Q contribution to the ¹⁴N shift of a given peak can be determined by subtraction of the ¹⁵N δ^iso_CS from the observed ¹⁴N shift, allowing the determination of χ_q. Previous studies have shown the experimentally measured χ_q to be consistent with previously determined or calculated values of C_Q and η for glycine and peptides of AGG and β-DA,^14,16,30 and has been used to investigate H-bonding in pharmaceuticals.²⁹ However, in order to quantitatively determine C_Q and η precisely from such data, η must be determined by fitting the ¹⁴N lineshape to simulations.

Fig. 1 Pulse sequences employed for the acquisition of the 2D-¹⁴N/¹H (A) and 3D-¹⁴N/¹H/¹H correlation (B) spectra reported in this study. The length of the excitation (τ_exc) and reconversion pulses (τ_rec) and the t₁ increments are chosen to ensure that the sequence is rotor synchronised, π/2 and π pulses are highlighted in black and grey respectively. For the 3D experiment, proton mixing during τ_m was conducted using a RFDR pulse train, pulses have been omitted for clarity.

The simulation of indirectly detected ¹⁴N lineshapes is difficult since the lineshape depends on numerous parameters, including quadrupolar broadening, and the orientation of the quadrupolar tensor with respect to the dipolar and CSA tensors. Therefore, determination of ¹⁴N NQI parameters has not been previously attempted due to (a) poor efficiency of indirect detection methods leading to noisy and ill-defined ¹⁴N lineshapes unsuitable for fitting, and (b) computationally expensive nature of simulating these experiments. In this work, we address both of these issues and present a highly efficient ¹H/¹⁴N correlation experiment, and fast and accurate simulations which in combination allow the de novo determination of ¹⁴N NQI parameters from organic solids with a variety of ¹⁴N sites with various NQI parameters. These fast and accurate numerical simulations of each ¹⁴N site allows the fitting of simulations to experimental lineshapes and the simultaneous determination of ¹⁴N NQI parameters at multiple sites from a 2D data set.

Materials and methods

Materials

Samples of histidine hydrochloride monohydrate (His·HCl·H₂O), L-histidine (L-His), N-acetyl-valine (NAV) and valine were purchased from Sigma-Aldrich (UK) and used without further purification.

Solid-state NMR experiments

Solid-state NMR experiments on His·HCl·H₂O and L-His were performed on an Agilent DDR2 spectrometer operating at 14.1 T (Larmor frequencies of 600 MHz and 43.4 MHz for ¹H and ¹⁴N) equipped with a 1.6 mm triple resonance MAS probe tuned in double resonance mode. MAS frequencies were 40 kHz for the L-His sample and 35.5 kHz for the His·HCl·H₂O sample.

The pulse sequence for indirect detection of ¹⁴N via¹H used in this work is shown in Fig. 1. Pulse lengths for ¹H pulses were π/2 = 1.55 μs, π = 3.10 μs on both samples, ¹⁴N pulses for excitation and reconversion were applied at 62.5 kHz for 575 μs, and 30 kHz for 390 μs for L-His and His·HCl·H₂O, respectively. The L-His spectrum was recorded with 112 scans per t₁ increment, with 160 complex increments and a recycle delay of 2 s and the His·HCl·H₂O spectrum was recorded with 64 scans and 254 t₁ increments with a recycle delay of 2 s. Both were recorded using States-TPPI.³³ Both datasets were zero-filled to 2048 × 2048 points and 2D Fourier transformed without a window function.

Experiments on NAV were performed on a Bruker Avance II spectrometer at 20 T (Larmor frequencies of 850 MHz and 61.4 MHz for ¹H and ¹⁴N) using a JEOL 1 mm double resonance MAS probe. The sample was spun with a MAS frequency of 78 kHz. Spectra were acquired using the pulse sequence in Fig. 1. ¹H pulses were π/2 = 1.1 μs, π = 2.2 μs and ¹⁴N excitation and reconversion pulses were applied at 72 kHz for 370 μs. 128 complex t₁ increments were recorded with 136 scans per increment, in a phase sensitive manner, using States-TPPI.³³ The recycle delay was 3 s. Data was zero-filled to 2048 points in each dimension before 2D Fourier transform. 3D ¹⁴N resolved ¹H/¹H correlation spectra were acquired the pulse scheme shown in Fig. 1B. Following ¹⁴N evolution, protons were allowed to evolve under the proton chemical shift prior a period of RFDR proton/proton mixing³⁴ prior to detection. Data was acquired with States-TPPI³³ in both indirect dimensions with 16 and 32 increments in the indirect ¹⁴N and ¹H dimensions respectively. Data was processed in nmrPipe³⁵ and visualised in Analysis 2.4.0, modified to include ¹⁴N parameters.³⁶ In all spectra, the ¹⁴N dimension is referenced to the ¹⁴N resonance of NH₄Cl at 39.3 ppm, ensuring that the ¹⁴N shifts can be compared directly with values on the scale typically used for referencing ¹⁵N in biological solids.³⁷

Numerical simulations

All NMR simulations were performed with the Spinach library versions 1.6 and 2.2.³⁸ Each nitrogen site simulated was approximated as a pair of nuclei comprising the ¹⁴N nucleus and the closest bound proton. Simulations included dipolar coupling, CSA and NQI parameters for both spins that were initially obtained from CASTEP calculations³⁹ or literature values. These initial calculated and literature values are shown in Table 1. Relative orientations of ¹⁴N NQI and ¹⁴N and ¹H CSA tensors were also obtained from the literature, and are also given in Table 1, defined with respect to the PAS of the ¹H–¹⁴N dipolar tensor. Relaxation was neglected in the simulations, and an apodization function applied to simulated FIDs before Fourier transform that reflected the effective T₂ of the experimental ¹⁴N signal. An input script for the experiment described in this paper is available in the latest release of the Spinach library. For simulations on sites in L-His and His·HCl·H₂O, powder averaging was performed over 770 pairs of α and β angle orientations calculated using the Lebedev method. A Floquet rank of 45 was sufficient for convergence for all sites in L-His and His·HCl·H₂O except the N_δ site of His·HCl·H₂O, where a rank of 55 was required due to the increased C_Q magnitude. Simulations of NAV used 1454 α and β angle orientations and a Floquet rank of 55. To fit the experimentally determined lineshapes the simulated ¹⁴N signals, C_Q and η were systematically varied in steps of 50 kHz and 0.1 respectively and the RMSD between experiment and simulation calculated.

Table 1 Parameters describing the spin interactions and their relative geometries found in the compounds used in this study

Sample	Site	δ (ppm)	C Q (MHz)	η	Orientation (α, β, γ)
					^14N CQ	^14N CSA	^1H CSA
a Measured on ^15N using CPMAS. b Ref. 7. c Calculated values using CSD reference code: HISTCM12. d Ref. 43 and 44. As referenced to NH4Cl at 39.3 ppm. e Ref. 45–47. As referenced to NH4Cl at 39.3 ppm. f Ref. 48. g Ref. 49. h Ref. 50.
His·HCl·H2O	NH3^+	47.3^a^,^d	1.32^c	0.06	0, 0, 0	—	109, 72, 172
	Nδ	189.8^a^,^d	1.53^c	0.23	0, 90, 0	−71.18, 1.5, −7.2	102.1, 66, −84
	Nε	177.2^a^,^d	1.33^c	0.94		−75, 181.5, −7.2	90, 196, −86
L-His	NH3^+	41.6^a	1.22^b	0.15	0, 0, 0	—	109, 72, 172
	Nε	168.9^a	1.44	0.92	0, 90, 0	75, 181.5, −7.2	90, 196, −86
NAV	N1	127.7	3.21^f	0.32	13.2, 90, 103^g	51, 20, 0^e	103.2, 0, 193^h

---

CASTEP calculations

To calculate the NQI we used the CASTEP density function theory (DFT) package^39–42 which uses the gauge including projector augmented wave (GIPAW) algorithm. We used the Perdew–Burke–Ernzerhof (PBE) generalised gradient approximation (GGA) with ultrasoft pseudopotentials and 0.1k points ų. We tested the value of the NQI by converging against the plane-wave energy cut-off tolerance.

Results and discussion

Histidine hydrochloride monohydrate and L-histidine

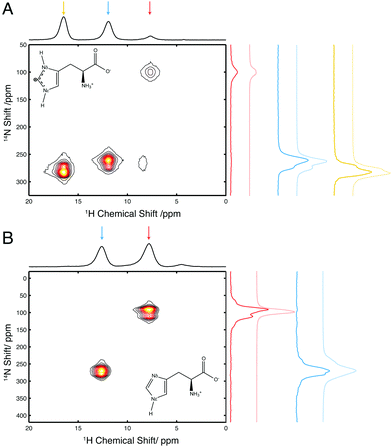
In order to assess the effects of alternate hydrogen bonding patterns and changes in local geometry on ¹⁴N NQI parameters at a number of different nitrogen sites, and how these changes affect ¹⁴N lineshapes and peak positions, we initially investigated samples of L-His and His·HCl·H₂O. These two salts of histidine exhibit different protonation states (see Fig. 2) and H-bonding networks, resulting in a variation in local electronic structure with the associated variation in ¹⁴N NQI parameters (Table 1).

Fig. 2 ¹H/¹⁴N correlation spectra of two forms of histidine at 14.1 T. Spectrum of His·HCl·H₂O recorded at 35.5 kHz (A) MAS frequency L-His spectrum (B). Recorded at 40 kHz MAS frequency. Experimental (solid) and simulated (dashed) projections through the ¹⁴N dimension are plotted for each spectrum at the NH₃⁺ site (red), the N_ε site (blue) and the N_δ site (yellow). The projections are normalised to the maximum peak intensity in each respective spectrum.

Fig. 2A shows the ¹H/¹⁴N correlation spectrum of His·HCl·H₂O, recorded at 14.1 T, under 35.5 kHz MAS. Three peaks are observed, corresponding to the three protonated nitrogen sites in this molecule. The NH₃⁺, N_δ and N_ε and sites appear at ¹⁴N shifts of 100 ppm, 263 ppm and 280 ppm, respectively. The transfer efficiency of this experiment was 27.5% at N_ε, 24.4% at N_δ and 7.5% at NH₃⁺ sites, expressed relative to a ¹H spin echo on the same sample using delays equal to the length of applied ¹⁴N pulses. These efficiencies are comparable with or in excess of those reported in the literature for the same or similar compounds acquired with both J- and D-HMQC sequences. Using the J-HMQC sequence under ultrafast MAS (90 kHz), which is optimal for the ¹H detected J-HMQC sequence since ¹H coherence lifetimes that these experiments are particularly sensitive to increase significantly with MAS, ¹⁴N transfer efficiencies of 7.55% and 9.75% with respect to ¹H spin echo were recently reported for the N_ε and N_δ sites in His·HCl·H₂O.⁵¹ Using a D-HMQC sequence, with R³ recoupling, transfer efficiencies of 5–6% have been reported for the NH₃⁺ site in glycine at 20 kHz MAS.¹⁶ The experiment performed here was optimised (in terms of ¹⁴N offset and pulse length) such that efficiency was maximally distributed over the two heterocyclic ¹⁴N sites, and as such, ¹⁴N pulse widths and amplitudes are possible that increase the efficiency at any of the three sites, at the expense of signal intensity at the other sites. This results in a spectrum with a quality and signal/noise ratio such that subtle spectral features such as the shoulders on the peaks of N_ε and N_δ are observed which can aid in the characterisation of the quadrupolar interaction.

Fig. 2B shows a ¹H/¹⁴N correlation spectrum of L-His, recorded at 14.1 T under 40 kHz MAS. In this spectrum only two peaks are observed which are the NH₃⁺ and N_ε sites at 100 ppm and 278 ppm ¹⁴N shifts, respectively; the unprotonated N_δ site is not detected. Similar transfer efficiencies were achieved as those for His·HCl·H₂O, with 20.0% and 16.6% of ¹H spin echo signal recorded at N_ε and NH₃⁺ sites, respectively. This experiment was optimised for an even distribution of intensity between the two ¹⁴N sites and could be optimised to achieve a higher signal intensity at one site, potentially at the expense of that at the other.

Comparing the peaks from the N_ε and NH₃⁺ sites in L-His to the peaks from the same sites in His·HCl·H₂O, there are differences in both ¹⁴N frequency and peak shape. The ¹⁴N frequency may be used to determine ¹⁴N δ^iso_Q at each site. Contributions from the ¹⁴N chemical shift and ¹⁴N δ^iso_Q to the observed ¹⁴N shift at each peak in the spectra of L-His and His·HCl·H₂O are separated by subtracting the contribution from the isotropic chemical shifts, which are shown in Table 1. These were determined from a separate natural abundance ¹⁵N CPMAS experiment performed on each sample. For both materials, the measured values of ¹⁴N δ^iso_Q are tabulated in Table 2.

Table 2 Calculated and experimental ¹⁴N δ^iso_Q values for the samples used in this study

Sample	Site	δ ^isoQ expt.^a (ppm)	δ ^isoQ calc.^b (ppm)
a The centre of gravity of the ^14N peak in the indirect dimension – ^15N δ^isoCS from Table 1. A ±5 ppm error is associated with measuring the ^14N frequency from the spectra. b Calculated from CQ and η from Table 1 using eqn (2), with Larmor frequencies calculated from B0 = 14.1 T for histidine sites, and B0 = 20.0 T for NAV.
His·HCl·H2O	NH3^+	55.4	69.5
	Nδ	90.2	94.9
	Nε	85.8	91.1
L-His	NH3^+	58.4	59.7
	Nε	105.4	105.9
NAV	N1	207.1	211.5

---

The δ^iso_Q can be used to estimate the magnitude of the C_Q and η at each site, using eqn (1)–(3). A contour plot of values of δ^iso_Q at 14.1 T, calculated from eqn (1), as a function of the magnitude of the C_Q and η are shown in Fig. S1 (ESI†). As expected from eqn (2), C_Q and η are correlated, however at this field the δ^iso_Q shows only a limited dependence on the asymmetry parameter η and thus C_Q can be readily constrained to a range of ∼200 kHz irrespective of the asymmetry parameter. In L-His the NH₃⁺ and N_ε sites are determined to have C_Q tensor magnitudes of 1.00–1.15 MHz and 1.37–1.58 MHz respectively, and the NH₃⁺, N_ε and N_δ sites in His·HCl·H₂O have magnitudes of 1.00–1.15 MHz, 1.28–1.48 MHz and 1.32–1.52 MHz, for all possible values of η. The C_Q of the NH₃⁺ site in both compounds can be constrained to a smaller range of C_Q magnitudes, since χ_q and, therefore, ¹⁴N δ^iso_Q is less dependent on η when the C_Q is smaller. The agreement of the ¹⁴N δ^iso_Q determined from indirect detection methods in this paper, as compared to those calculated from literature values for ¹⁴N chemical shift and NQI tensors in the histidine compounds studied here is demonstrated in Table 2. In general, the ¹⁴N δ^iso_Q observed in this work is smaller than that expected from literature values obtained by other techniques, or CASTEP calculated values. This discrepancy is most severe at the amine sites of both histidine molecules, with the His·HCl·H₂O experimental NH₃^{+ 14}N δ^iso_Q being 14.1 ppm lower than the calculated value, and that site in L-His was found to be 9 ppm lower than the literature/calculated value. At the remaining heterocyclic sites, the N_ε site in His·HCl·H₂O was found to deviate most from the ¹⁴N δ^iso_Q value calculated from literature NQI parameter values, at 5.3 ppm. These deviations, being most severe for the highly mobile primary amine sites in histidine compounds, may be due to comparisons being made with NQI parameters determined by different techniques at cryogenic temperatures rather than room temperature, freezing out motions that could scale the ¹⁴N NQI in our experiments, or comparisons with CASTEP calculations that do not take into account molecular motions.

Quantitative analysis of histidine spectra

Having recorded indirect ¹⁴N detected spectra with very high efficiencies, the quality of data was high enough to observe subtle spectral features in the ¹⁴N lineshapes, for example, the shoulders on the sides of N_ε and N_δ peaks in the His·HCl·H₂O spectrum. As it is not possible to accurately determine C_Q and η from the quadrupolar product alone, a more accurate analysis was undertaken fitting the ¹⁴N lineshapes in the indirect dimension. Numerical simulations were fitted to the experimentally determined lineshapes at each ¹⁴N site in the two histidine compounds, by systematically searching a C_Q and η parameter space spanning C_Q = ±0.25 MHz and η = ±0.25 of the published or calculated values. Plots of the root mean squared deviation (RMSD) between simulated and experimental spectra for each of the ¹⁴N sites in the histidine samples studied is shown in Fig. 3. The fits of these lineshapes were conducted with the quadrupolar and chemical shielding tensors oriented with respect to the ¹H/¹⁴N dipolar coupling according the values given in Table 1. Simulations indicate that these parameters do indeed contribute to the overall ¹H/¹⁴N lineshape, however for compounds with a small C_Q these effects are negligible with the linewidths that are experimentally obtainable.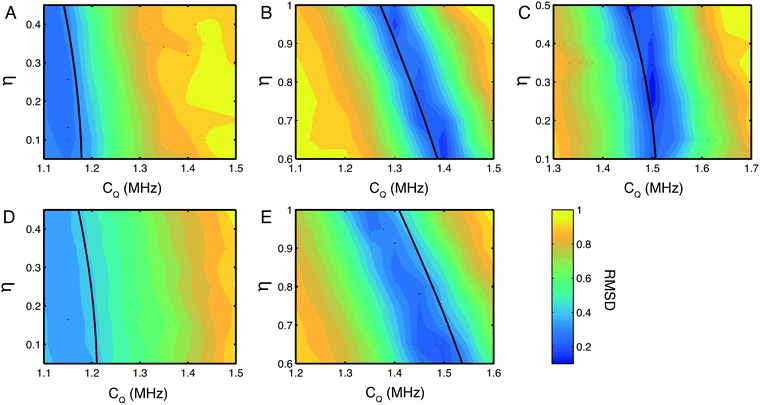

Fig. 3 RMSD plots of simulated and experimental ¹⁴N lineshapes. Plots for the NH₃⁺ (A) N_ε (B) and N_δ (C) sites in His·HCl·H₂O and the NH₃⁺ (D) and N_ε (E) sites in L-His. The magnitude of the C_Q was arrayed in steps of 0.05 MHz from −0.25 to +0.25 MHz from the initial value, and η was arrayed in steps of 0.05 from −0.25 to +0.25 about a region spanning the predicted η for each nitrogen site based on the figures in Table 1. In all cases, contour lines are spaced by 5% of the maximum RMSD value. Errors estimated at the 10% RMSD level are C_Q = 1.1 ± 0.3 MHz, η = 0.3 ± 0.3 for (A), C_Q = 1.4 ± 0.08 MHz, η = 0.64 ± 0.04 for (B), C_Q = 1.5 ± 0.1 MHz, η = 0.26 ± 0.06 for (C), C_Q 1.1 ± 0.3 and η poorly defined (see text for discussion) for (D), C_Q = 1.4 ± 0.15 MHz, η = 0.90 ± 0.06 for (E). The single black contour line in each plot indicates the δ^iso_Q for each site calculated from the measured ¹⁴N shift δ^iso_Q.

There is a strip of relatively good agreement (RMSD < ∼0.3) through the RMSD plot for each ¹⁴N site where the simulated ¹⁴N δ^iso_Q is consistent with that observed experimentally. A single black contour line through each plot marks the experimentally observed ¹⁴N δ^iso_Q, which are also plotted on the contour plot in Fig. S1 (ESI†), and tabulated in Table 2. This line generally coincides with the area of lowest RMSD in each plot. This shows that the largest contribution to the quality of the simulations fit is determined from the ¹⁴N δ^iso_Q, which is to be expected since it determines the position of the peak. In the RMSD plot for the N_δ of His·HCl·H₂O, Fig. 3C, a single RMSD minimum where the RMSD is <0.15 (darkest blue contours) is observed. This covers a range of C_Q = 1.49–1.51 MHz, and η = 0.22–0.34, which is in close agreement with the CASTEP calculated values at this site, C_Q = 1.53 MHz, and η = 0.23, as well as literature values of C_Q = 1.47 MHz, and η = 0.27.⁵² Additionally, visual comparison of the simulated lineshape with the experimental lineshape (Fig. 2A, yellow traces) shows a good agreement. This plot demonstrates that using a simulation fitting approach, one can define η to a range of ∼±0.1, which allows the C_Q to be determined with a precision of tens of kHz, which is at least an order of magnitude more precise than one can achieve considering only the ¹⁴N δ^iso_Q.

In the RMSD plots for the N_ε sites of both His·HCl·H₂O (Fig. 3B) and L-His (Fig. 3E), the fit of the lineshape with respect to η is somewhat less robust. In the case of the N_ε site in His·HCl·H₂O, two RMSD minima <0.2 are observed, at C_Q = 1.29–1.3 MHz, η = 0.93–0.97, and C_Q = 1.39–1.41 MHz, η = 0.60–0.68. The former of these minima, however, is consistent with the calculated values for this site, of C_Q = 1.33 MHz, η = 0.94, as well as reported literature values of C_Q = 1.29 MHz, η = 0.95.⁵² For the N_ε site in L-His, the same general pattern is observed, with two RMSD minima in similar positions with respect to η as those observed at the same site in His·HCl·H₂O (C_Q = 1.35 MHz, η = 0.95–1.00, and C_Q = 1.5 MHz, η = 0.60–0.65). However, the fit is not as good as that of the N_ε site in the hydrochloride salt; in L-His the RMSD minima are broader, and the RMSD is not as low (minimum RMSD = 0.24). This is probably due to there being less well-defined features in the experimental lineshape at this site (as shown in Fig. 2B) compared to the N_ε in His·HCl·H₂O (Fig. 2A). However, the N_ε sites are expected to have similar chemical environments and hydrogen bond geometries, and therefore similar ¹⁴N spectral parameters in terms of their ¹⁴N EFG and CSA tensors which give rise to the features observed in the ¹⁴N lineshapes, and one of the RMSD minima (at C_Q = 1.35 MHz, η = 0.95–1.00) is consistent with expected values.

The NH₃⁺ sites in both His·HCl·H₂O and L-His show a poor fit of the simulated lineshape with respect to η, with the minimum RMSD encompassing almost the whole range of η values simulated, and not falling below RMSD = 0.3. This means it is not possible to use these plots to constrain the C_Q at either site more precisely than was achieved by considering simply the ¹⁴N δ^iso_Q.

In the case of the His·HCl·H₂O the rather poorly defined minima reflects the featureless nature of the peak without any discontinuities, shoulders or splittings, making a distinctive fit difficult. This may be due to the fast ¹H T₂* decoherence at this site leading to a broadening of the signal and the loss of any distinctive features, indeed simulated spectra exhibited well defined splittings and shoulders before the application of the apodization to match the experimentally observed decay. We attribute this rapid relaxation to the molecular motions present at the site,^53–55 which, in the case of NH₃⁺ groups have previously been shown to influence the SQ ¹⁴N lineshape.¹⁸

At the NH₃⁺ site in L-His, a well-defined splitting was observed in the ¹⁴N lineshape. However, the fit of the simulated spectra to this lineshape was the least satisfactory of all those investigated here, with a minimum RMSD = 0.35. As the experimental and simulated slices (Fig. 2B, red traces) show, the experimental spectrum observed was significantly broader, with more features, than the best fit simulated spectrum. The reason for this may be that at the NH₃⁺, the ¹⁴N is coupled to three separate protons, which cannot be resolved in the ¹H spectrum, and so their contributions to the ¹⁴N lineshape are superimposed in the ¹⁴N dimension. The simulated lineshape only takes into account an approximation of the spin system with ¹⁴N coupled to a single amine proton. This would mean that the simulation only accounted for part of the experimental lineshape, and that the remaining features were due to coupling to the other protons at the NH₃⁺. Similar effects could also arise through the presence of conformational disorder in the sample or the presence of multiple polymorphs.

The differences observed between the fitted NH₃⁺ lineshape and those experimentally obtained may also reflect the limitations of our current simulations which ignore the effects of relaxation and motional processes. Although such effects could be incorporated into the calculations, these simulations are already computationally demanding and, practically, close to the limit of what we can achieve in a reasonable timeframe (several weeks of supercomputer time) when fitting a grid of parameters to experimental data. In contrast; fits of the heterocyclic ¹⁴N sites exhibit a better fit with the experimental data, with the C_Q and η in good agreement with published or calculated values. This is particularly clear for the N_δ site where the larger C_Q is larger.

N-Acetyl-valine spectrum

Further proton detected experiments were performed on NAV (see Fig. 4), which exhibits a larger NQI than the sites studied in the histidine samples, with a C_Q of 3.21 MHz and a η = 0.32,⁴⁸ and as such mirrors the properties of ¹⁴N sites within the peptide bonds of proteins and peptides.⁵⁶Fig. 4A shows a 2D ¹H/¹⁴N correlation spectrum recorded on a sample of NAV at 20.0 T (850 MHz ¹H Larmor frequency) and a MAS frequency of 78 kHz. Experiments were performed at a higher field with ultra-fast MAS in order to optimise conditions for proton detection on this challenging, high-C_Q sample. The increased field and MAS frequency, significantly enhances the sensitivity of the experiment, lengthening coherence lifetimes and reducing the ¹H homogeneous linewidth. The ¹⁴N shift of the amide ¹⁴N in NAV at this field is 335 ppm. From this shift, a ¹⁴N δ^iso_Q = 207.3 ppm is calculated, by subtracting the δ^iso_cs of 127.7 ppm (measured by ¹⁵N CPMAS). This agrees well with the expected ¹⁴N δ^iso_Q value of 211.5 ppm calculated for this field from literature values.⁴⁸ The efficiency of the two-way ¹⁴N transfer is 9% with respect to the ¹H spin echo signal under the same conditions. This is lower than the efficiencies of the proton detected experiment generally observed on the lower magnitude C_Q sites in the histidine compounds. This is a trend observed in all indirect ¹⁴N detection experiments and can be attributed to the increased magnitude of the ¹⁴N C_Q in NAV, which is likely to mean that the pulses applied on the ¹⁴N channel excite the far broader ¹⁴N spectrum to a lesser extent.

Fig. 4 ¹H/¹⁴N correlation spectrum of NAV at 20 T. Spectrum of NAV recorded at 78 kHz MAS. Experimental (red) and simulated (blue) projections through the ¹⁴N dimension are shown. (A) Plot of RMSD between experimental and simulated spectra of NAV at 20 T (B).

Quantitative analysis of N-acetyl-valine spectra

A quantitative analysis of the NAV was conducted in a similar manner to that utilized for the histidine compounds. A plot of the ¹⁴N δ^iso_Q, calculated from eqn (2), as a function of C_Q and η at 20.0 T, with the experimentally measured NAV ¹⁴N δ^iso_Q marked, is shown in Fig. S2 (ESI†). From this plot, one can read off the upper and lower limits placed on the C_Q at the ¹⁴N site in NAV by the ¹⁴N δ^iso_Q and determine the range of C_Q magnitudes consistent with the ¹⁴N δ^iso_Q as 2.83–3.26 MHz, for all values of η. This range of 430 kHz is far larger than the range of ∼200 kHz that could be obtained for the moderate C_Q (1.0–1.5 MHz) sites found in histidines at 14.1 T. This is since when the C_Q is large, the effects of η on the ¹⁴N δ^iso_Q will be larger, as evident from eqn (2), since η and C_Q are correlated, and the contribution of η is scaled by the C_Q magnitude.

Fig. 4B shows a contour plot of the RSMD of simulated spectra with respect to the experimental ¹⁴N lineshape in NAV as a function of the C_Q and η used in the simulations. A comparison of the best-fit ¹⁴N simulated lineshape with the experimental lineshape is seen in the projections in Fig. 4. The quality of the fit is high, with a minimum RMSD = 1.5, however the RMSD minimum is relatively broad; covering a region of C_Q magnitude of 75 kHz (C_Q = 3.1 MHz–C_Q = 3.175 MHz), and range of η values of 0.32 (0–0.32). The range of values covered by this RMSD minimum slightly underestimates the literature values of C_Q = 3.21 MHz, η = 0.32.⁴⁸ However, the black contour line which indicates the ¹⁴N δ^iso_Q calculated from the measured ¹⁴N shift at the centre of gravity of the ¹⁴N lineshape is also underestimated by the best RMSD fit, and in fact agrees very well with the literature values. The lack of accuracy with which the simulations fit the data suggest that there are features of the experimental ¹⁴N lineshape that are not accounted for in the simulations. The reason for this is unclear. Simulations to ascertain if the relative orientations of the quadrupolar, dipolar and chemical shift anisotropy influenced the lineshape were conducted (see Fig. S3 and S4, ESI†). Simulations in the absence of the chemical shielding anisotropy (CSA) (Fig. S3, ESI†) show that the proton lineshape is strongly correlated to the β Euler angle describing the orientation of the quadrupolar tensor with respect to the ¹H/¹⁴N dipolar coupling tensor, whilst the influence of the corresponding α Euler angle is limited to the lineshape. Similarly, introduction of the CSA into the simulations (Fig. S4, ESI†) resulted in minor changes to the lineshape. Although the effects of tensor orientation are pronounced when the linewidths are small, many of these factors are masked with the currently attainable experimental resolution, which together with the computationally demanding nature of the simulations and large parameter space precludes a more rigorous statistical fitting of the lineshape. Alternatively, it is plausible that the signal is broadened or shifted by higher-order terms (>2) in the quadrupolar Hamiltonian that are not accounted for in the simulations and not removed by MAS. For sites with lower (<1.5 MHz) quadrupolar couplings, it was verified that these terms did not affect the simulated lineshapes. However, this was not verified for the case where the quadrupolar coupling was large (∼3 MHz) and high order terms are expected to be more significant, as running the simulations with the full Hamiltonian was found to be prohibitively time consuming. Finally, it may be that the ¹⁴N spectrum of this site is broadened by high mobility of the amide nitrogen, although we acknowledge that this is not reflected in the size of the quadrupolar interaction.

Multidimensional ¹⁴N correlation spectroscopy

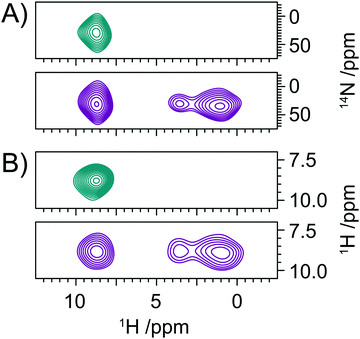
The quadrupolar interaction provides a sensitive reporter of secondary structure within proteins, with variations of up to 200 kHz reported between alpha-helical and beta-sheet structures, corresponding to variation in δ^iso_Q of ∼130 ppm in the proton detected spectra reported here. Despite the large variation in δ^iso_Q reported for proteins, for larger biomolecules its application will remain challenging due to the limited chemical shift dispersion in the amide protons. Although further enhancements in resolution and sensitivity can be realised through the application of faster MAS and higher ¹⁴N rf fields,^26,32 for larger biomolecules it is clear that higher-dimensionality spectra will be required to aid resolution and assignment. In Fig. 1B we describe a 3D experiments which allows the acquisition of a ¹⁴N resolved ¹H/¹H correlation experiment. Analogous in many ways to the ¹⁵N filtered ¹H/¹H NOESY experiment frequently employed in the liquid state, the ¹H/¹H correlations are now resolved according to the δ^iso_Q of the adjacent ¹⁴N site. The efficiency of the experiment ensures that such data sets can be acquired in as little as 2 days, with the overall duration limited by the phase cycling employed (Fig. 5).

Fig. 5 Slices extracted from a 3D, ¹⁴N resolved ¹H/¹H correlation spectrum of valine with no proton/proton mixing (teal), and 24 rotor cycles of RFDR mixing (purple). ¹H/¹⁴N planes (A) and their respective ¹H/¹H planes (B).

Conclusions

We have demonstrated the application of a novel method of indirect detection of ¹⁴N via¹H under moderate and fast MAS frequencies, applied to two forms of histidine and NAV. Spectra with up to 27.5% efficiency can be recorded using this method, resulting in a large increase in S/N and spectral quality, over previous methods. The data presented have been fitted to simulated lineshapes to extract NQI parameters for nitrogen sites in different chemical environments with increased precision. The ¹H detected ¹⁴N experiments described here are not as limited in the number of sites that can studied as previous methods such as piecewise detection, indeed the variation observed in C_Q served to enhance the resolution. Furthermore, exploitation of ¹H detection facilitates its application to unlabelled biomolecules, providing a viable route to study the structure and dynamics complex natural organic and biomolecular systems.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by The Wellcome Trust (PTFW and MC), EPSRC (EP/H003789/1, IK; EP/M023664/1, MC/PTFW/IK), The University of Southampton (JJ), and The Royal Society University Research Fellowship (MC). IK thanks EPSRC for an Impact Acceleration grant, and Jos Martin of MathWorks for technical support. IH thanks The Higher Committee for Education Development in Iraq for financial support. The UK 850 MHz solid-state NMR Facility instruments used in this research were funded by EPSRC and BBSRC, as well as the University of Warwick, including via part funding through Birmingham Science City Advanced Materials Projects 1 and 2 supported by Advantage West Midlands (AWM) and the European Regional Development Fund (ERDF). The authors acknowledge the use of the IRIDIS High Performance Computing Facility, and associated support services at the University of Southampton, in the completion of this work.

References

1. K. J. Harris, S. L. Veinberg, C. R. Mireault, A. Lupulescu, L. Frydman and R. W. Schurko, Chemistry, 2013, 19, 16469–16475.
2. L. A. O'dell, R. W. Schurko, K. J. Harris, J. Autschbach and C. I. Ratcliffe, J. Am. Chem. Soc., 2011, 133, 527–546.
3. S. L. Veinberg, Z. W. Friedl, K. J. Harris, L. A. O'Dell and R. W. Schurko, CrystEngComm, 2015, 17, 5225–5236.
4. R. Tycko and S. J. Opella, J. Am. Chem. Soc., 1986, 108, 3531–3532.
5. R. Tycko and S. J. Opella, J. Chem. Phys., 1987, 86, 1761.
6. R. Tycko, P. L. Stewart and S. J. Opella, J. Am. Chem. Soc., 1986, 108, 5419–5425.
7. L. A. O'Dell and A. Brinkmann, J. Chem. Phys., 2013, 138, 064201.
8. L. A. O'Dell, R. He and J. Pandohee, CrystEngComm, 2013, 15, 8657.
9. L. A. O'dell and C. I. Ratcliffe, Chem. Phys. Lett., 2011, 514, 168–173.
10. A. J. Rossini, L. Emsley and L. A. O'Dell, Phys. Chem. Chem. Phys., 2014, 16, 12890–12899.
11. I. M. Haies, J. A. Jarvis, H. Bentley, I. Heinmaa, I. Kuprov, P. T. F. Williamson and M. Carravetta, Phys. Chem. Chem. Phys., 2015, 17, 6577–6587.
12. Y. Nishiyama, M. Malon, Z. Gan, Y. Endo and T. Nemoto, J. Magn. Reson., 2013, 230, 160–164.
13. I. Haies, J. Jarvis, L. J. Brown, I. Kuprov, P. T. F. Williamson and M. Carravetta, Phys. Chem. Chem. Phys., 2015, 17, 23748–23753.
14. Z. H. Gan, J. Am. Chem. Soc., 2006, 128, 6040–6041.
15. Z. H. Gan, J. Magn. Reson., 2007, 184, 39–43.
16. Z. H. Gan, J. P. Amoureux and J. Trebosc, Chem. Phys. Lett., 2007, 435, 163–169.
17. S. Cavadini, A. Abraham and G. Bodenhausen, J. Magn. Reson., 2008, 190, 160–164.
18. S. Cavadini, A. Abraham, S. Ulzega and G. Bodenhausen, J. Am. Chem. Soc., 2008, 130, 10850–10851.
19. S. Cavadini, S. Antonijevic, A. Lupulescu and G. Bodenhausen, ChemPhysChem, 2007, 8, 1363–1374.
20. S. Cavadini, S. Antonijevic, A. Lupulescu and G. Bodenhausen, J. Magn. Reson., 2006, 182, 168–172.
21. S. Cavadini, A. Lupulescu, S. Antonijevic and G. Bodenhausen, J. Am. Chem. Soc., 2006, 128, 7706–7707.
22. S. Cavadini, V. Vitzthum, S. Ulzega, A. Abraham and G. Bodenhausen, J. Magn. Reson., 2010, 202, 57–63.
23. V. Vitzthum, M. A. Caporini and G. Bodenhausen, J. Magn. Reson., 2010, 205, 177–179.
24. V. Vitzthum, M. A. Caporini, S. Ulzega and G. Bodenhausen, J. Magn. Reson., 2011, 212, 234–239.
25. V. Vitzthum, M. A. Caporini, S. Ulzega, J. Trebosc, O. Lafon, J. P. Amoureux and G. Bodenhausen, J. Magn. Reson., 2012, 223, 228–236.
26. Y. L. Hong, T. Asakura and Y. Nishiyama, ChemPhysChem, 2018, 19, 1841–1845.
27. G. N. M. Reddy, M. Malon, A. Marsh, Y. Nishiyama and S. P. Brown, Anal. Chem., 2016, 88, 11412–11419.
28. D. Carnevale, X. Ji and G. Bodenhausen, J. Chem. Phys., 2017, 147, 184201.
29. A. S. Tatton, T. N. Pham, F. G. Vogt, D. Iuga, A. J. Edwards and S. P. Brown, Mol. Pharmaceutics, 2013, 10, 999–1007.
30. A. S. Tatton, T. N. Pham, F. G. Vogt, D. Iuga, A. J. Edwards and S. P. Brown, CrystEngComm, 2012, 14, 2654.
31. Y. Nishiyama, Y. Endo, T. Nemoto, H. Utsumi, K. Yamauchi, K. Hioka and T. Asakura, J. Magn. Reson., 2011, 208, 44–48.
32. J. A. Jarvis, I. M. Haies, P. T. F. Williamson and M. Carravetta, Phys. Chem. Chem. Phys., 2013, 15, 7613–7620.
33. D. Marion, M. Ikura, R. Tschudin and A. Bax, J. Magn. Reson., 1989, 85, 393–399.
34. A. E. Bennett, J. H. Ok, R. G. Griffin and S. Vega, J. Chem. Phys., 1992, 96, 8624–8627.
35. F. Delaglio, S. Grzesiek, G. W. Vuister, G. Zhu, J. Pfeifer and A. Bax, J. Biomol. NMR, 1995, 6, 277–293.
36. W. F. Vranken, W. Boucher, T. J. Stevens, R. H. Fogh, A. Pajon, P. Llinas, E. L. Ulrich, J. L. Markley, J. Ionides and E. D. Laue, Proteins, 2005, 59, 687–696.
37. P. Bertani, J. Raya and B. Bechinger, Solid State Nucl. Magn. Reson., 2014, 61–62, 15–18.
38. H. J. Hogben, M. Krzystyniak, G. T. P. Charnock, P. J. Hore and I. Kuprov, J. Magn. Reson., 2011, 208, 179–194.
39. M. Profeta, F. Mauri and C. J. Pickard, J. Am. Chem. Soc., 2003, 125, 541–548.
40. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570.
41. C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101.
42. J. R. Yates, C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401.
43. S. Li, L. Zhou, Y. Su, B. Han and F. Deng, Solid State Nucl. Magn. Reson., 2013, 54, 13–17.
44. S. Li and M. Hong, J. Am. Chem. Soc., 2011, 133, 1534–1544.
45. D. K. Lee, Y. F. Wei and A. Ramamoorthy, J. Phys. Chem. B, 2001, 105, 4752–4762.
46. Y. F. Wei, D. K. Lee, A. E. McDermott and A. Ramamoorthy, J. Magn. Reson., 2002, 158, 23–35.
47. J.-S. Lee and A. K. Khitrin, Concepts Magn. Reson., Part A, 2008, 32, 56–67.
48. R. E. Stark, R. A. Haberkorn and R. G. Griffin, J. Chem. Phys., 1978, 68, 1996.
49. M. D. Esrafili, H. Behzadi and N. L. Hadipour, Biophys. Chem., 2008, 133, 11–18.
50. M. Bak, R. Schultz, T. Vosegaard and N. C. Nielsen, J. Magn. Reson., 2002, 154, 28–45.
51. M. K. Pandey and Y. Nishiyama, J. Magn. Reson., 2015, 258, 96–101.
52. C. A. Mcdowell, A. Naito, D. L. Sastry and K. Takegoshi, J. Magn. Reson., 1986, 69, 283–292.
53. S. E. Ashbrook, S. Antonijevic, A. J. Berry and S. Wimperis, Chem. Phys. Lett., 2002, 364, 634–642.
54. M. J. Thrippleton, M. Cutajar and S. Wimperis, Chem. Phys. Lett., 2008, 452, 233–238.
55. M. Chan-Huot, S. Wimperis, C. Gervais, G. Bodenhausen and L. Duma, ChemPhysChem, 2015, 16, 204–215.
56. J. A. Jarvis, I. Haies, M. Lelli, A. J. Rossini, I. Kuprov, M. Carravetta and P. T. F. Williamson, Chem. Commun., 2017, 53, 12116–12119.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp06276e

‡ Current address: Department of Life Sciences, Imperial College, SW7 2AZ, London, UK.

---