A new ab initio modeling scheme for the ion self-diffusion coefficient applied to the ε-Cu3Sn phase of the Cu–Sn alloy†
Received
8th October 2018
, Accepted 25th January 2019
First published on 18th February 2019
Abstract
We present a new scheme for modeling of the ion self-diffusion coefficient. Our scheme broadens the applicable scope of the ‘ab initio + modeling’ approach, which combines modeling of the self-diffusion coefficient with ab initio predictions. Essential concepts in our scheme are ‘domain division’ and ‘coarse-graining’ of the diffusion network, according to calculated barrier energies. With the former concept, the diffusion network is divided into a few types of simple disjunct domains. Their networks are further simplified with the latter idea that groups some ion sites and regards them as just a single site. We applied this scheme to Cu diffusion in the ε-Cu3Sn phase of the Cu–Sn alloy and succeeded in reproducing experimental diffusion coefficients in a wide range of temperature.
1 Introduction
Ion diffusion attracts broad interest from material researchers because it dominates various important phenomena in solids such as corrosion, monotectoid reactions, fracture, and degradation. In order to elucidate a microscopic mechanism of ion diffusion, ab initio calculation is one of the most powerful tools. For example, it can evaluate barrier energies of diffusion routes, with such techniques as the nudged elastic band (NEB) method.1 Even also ion self-diffusion coefficients‡ have been reported theoretically2–7 combining ab initio predictions with modeling schemes such as the five-frequency model.8–10 However, these applications have been limited to just the simplest crystals, mainly due to the following reasons. First, systems appearing in practical situations often require a large size of the unit cell because of their long-range periodicity, which makes the calculation expensive, and often infeasible. This problem is especially severe, for example, when optimizing an ion path through a diffusion route using the NEB method, because it requires many force-field calculations for each of several transition structures. Second, it is always tough to take into account all of the ion diffusion processes, which is necessary to model the self-diffusion coefficient.
To overcome the difficulties, we introduce a couple of novel concepts in order to simplify the diffusion network. First, we classify the diffusion routes into three groups I–III, according to their barrier energies, ΔEI ≪ ΔEII ≪ ΔEIII. Since the barrier energy exponentially contributes to the diffusion coefficient (i.e. the Boltzmann factor), diffusion routes (III) can be excluded from the diffusion network. Then, the network may be divided into a few disjunct domains, and the expensive calculation for the large unit cell is replaced by cheaper calculations for these domains. This is the solution for the first difficulty. Second, the diffusion network in each domain is further simplified by coarse-graining: a vacancy moves almost freely through diffusion routes (I) compared with routes (II), so ion sites connected by routes (I) can be merged into just a single site. (We call it a representative site or rep-site.) Accordingly, the diffusion network falls into a coarse-grained one with the rep-sites, where it is much easier to model the self-diffusion coefficient by counting up possible diffusion processes.
Finally, we established a modeling scheme based on these concepts and applied it to obtain the Cu ion self-diffusion coefficient in the ε-Cu3Sn phase of the Cu–Sn alloy. This system is an excellent example because it has long-range periodic structure and abundant experimental data of the self-diffusion coefficient is available.11–16 The constructed model successfully reproduced the experiments in a wide range of temperature, better than a classical MD study by a digit.17 Also we verified how well our modeling takes into account diffusion processes. It affects the accuracy of the evaluation of the correlation factor, which is a key quantity of modeling. We confirmed that the obtained correlation factor is quite reasonable, compared to a reference value of a two-dimensional hexagonal lattice.
In this section we briefly explained two essential concepts, ‘domain division’ and ‘coarse-graining’, for ab initio modeling of diffusion coefficients. They are described further with an example of Cu ion diffusion in ε-Cu3Sn alloys and a brief explaination of how they are used to obtain the diffusion coefficients in Section 2. Detailed derivations of the formula are put in the ESI,† since they are too complicated and would make the main stream of the discussion unclear. The constructed model is carefully validated in Section 4 by comparing the self-diffusion coefficients with experimental values and, moreover, the correlation factor with the reference value. Finally, we summarize this work and review our scheme compared to the ab initio molecular dynamics method in Section 5.
2 Modeling
Domain division
The structure of the ε-Cu3Sn phase is shown in Fig. 1a, which has long-range periodicity. In the previous interpretation, it consists of unit cells of Cu3Ti-type structure with 1/2 shifts along the a-axis, every M/2 unit cell lining up along the b-axis. (M = 2, 4, 6, 8, and 12 have been reported experimentally.18,20) Our ab initio predictions revealed that ion jumps through diffusion routes passing between Sn sites hardly contribute to the self-diffusion because their barrier energies are much higher than the others by >30 kJ mol−1. After excluding these routes, the network is divided into two types of simple domains, Cu3Ti-type and D019-type, as shown in Fig. 1b. They exist in a ratio of (M − 2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, so the self-diffusion coefficient is given as a weighted average of those with their existence ratio:
2, so the self-diffusion coefficient is given as a weighted average of those with their existence ratio:| | 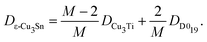 | (1) |
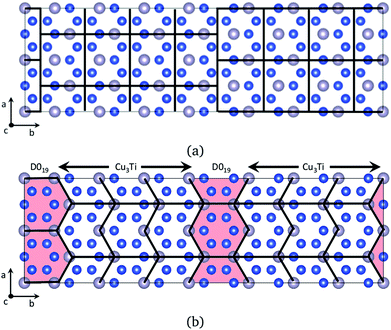 |
| | Fig. 1 A schematic picture of domain division for the ε-Cu3Sn structure.18 The blue balls represent Cu ions, and the gray balls Sn ions. Figure (a) shows the conventional interpretation for the long-range periodic structure. A Cu3Ti-type unit cell (surrounded by a thick line) is shifted by 1/2 a period along the a direction in fractional coordinates, every M/2 (M: periodicity) unit cell lining up along the b direction. Figure (b) shows our new interpretation. (M − 2)/2 unit cells of Cu3Ti-type structure and one D019-type unit cell appear periodically along the b direction. These pictures are made using VESTA.19 | |
Coarse-graining
Cu sites in the D019-type domain (Fig. 2) are positioned like hexagonal tubes composed of Cu sites surrounded by lines connecting Sn sites. Each tube consists of laminations of Cu ions arranged in a triangle shape, located in different ab-planes by 1/2 a period. (The hatched and the unhatched sites are on the different planes.) The barrier energy of route 3 is much higher than those of route 1 and 2 by >50 kJ mol−1, so ions almost independently diffuse in each hexagonal tube. Also, route 1 has a much lower barrier energy than route 2 by >40 kJ mol−1, so the vacancy much more easily moves in a triangle through route 1 than moving across two triangles through route 2. Therefore, the three sites forming the triangle are merged into just a single site (rep-site), which is named rep-site in the introduction. The diffusion network is coarse-grained into 1-dimensional ones along the c-axis composed of rep-sites as shown in Fig. 3. Since it is known that diffusion factors are zero in 1-dimensional lattices,21
 |
| | Fig. 2 Diffusion routes and barrier energies of Cu ions in the D019-type domain. The diffusion routes are shown as two-way arrows with their barrier energies. The blue balls represent Cu ions, and the gray balls Sn ions. The hatched balls are located on a c = 1/2 plane, and the unhatched ones are on a c = 0, 1 plane in fractional coordinates. Ion diffusion occurs in 1-dimensional tubes partitioned by the thick black lines because the energy barrier of route 3 across the thick lines is much higher than the others by >30 kJ mol−1. This picture is made using VESTA.19 | |
 |
| | Fig. 3 A schematic picture of coarse-graining for the D019-type domain. The open and closed stars represent a rep-site including a vacancy and a fully occupied one. Since ions seldom jump perpendicular to the c-axis, the coarse-grained network is almost 1-dimensional. | |
The diffusion network of the Cu3Ti-type domain is also coarse-grained using the same analogy, yet into 2-dimensional ones: the barrier energies of route 6,6′ are much higher than the others by >30 kJ mol−1 so ion diffusion occurs in each layer partitioned by the thick zig-zag lines drawn in Fig. 4. Also, the barrier energies of route 3,3′ are much lower than the others by ∼30 kJ mol−1, so the three sites connected by route 3,3′ can be merged into a rep-site. After coarse-graining, the diffusion network falls into 2-dimensional ones including two types of diffusion routes a and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) , as shown in Fig. 5. (Route a is parallel to the a-axis but route
, as shown in Fig. 5. (Route a is parallel to the a-axis but route ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) deviates from the c-axis.) In this case, the diffusion coefficient DCu3Ti has a finite value.
deviates from the c-axis.) In this case, the diffusion coefficient DCu3Ti has a finite value.
 |
| | Fig. 4 Diffusion routes of Cu ions in the Cu3Ti-type domain. The blue balls represent Cu ions, and the gray balls Sn ions. The hatched balls are located on a c = 1/2 plane, and the unhatched ones are on a c = 0, 1 plane in fractional coordinates. Three sites named top and bottom are merged into just a single site (rep-site). Diffusion routes connecting the adjacent rep-sites are shown as the red arrows (1,1′,2) and the blue ones (5), which are named route ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) and a respectively. Barrier energies of every route are listed below the figure. The diffusion network is partitioned by the thick zig-zag lines, because route 6, 6′ has much higher energy barriers than the others by >30 kJ mol−1. This picture is made using VESTA.19 and a respectively. Barrier energies of every route are listed below the figure. The diffusion network is partitioned by the thick zig-zag lines, because route 6, 6′ has much higher energy barriers than the others by >30 kJ mol−1. This picture is made using VESTA.19 | |
 |
| | Fig. 5 A schematic picture of coarse-graining for the Cu3Ti-type domain. The open and closed stars represent a rep-site including a vacancy and a fully occupied one. Since ions seldom jump in the perpendicular direction to the ac-plane, the coarse-grained network is almost 2-dimensional. The network contains two types of routes, a and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) . Route a is parallel to the a-axis, and meanwhile, route . Route a is parallel to the a-axis, and meanwhile, route ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) is not parallel to the c-axis. is not parallel to the c-axis. | |
Since the framework of ‘coarse-graining’ is based on the apparent differences in the barrier energies, one might worry about its general applicability when the barriers do not have such outstanding differences as in the present case. It is partly true that the applicability becomes limited, but it still works in the low temperature region: even with a smaller difference of the barrier energies like 1 kJ mol−1 compared to the case in Fig. 2 and 4, their Boltzmann factors differ by around ten times at 50 K. Meanwhile they surely become almost the same at 1000 K, and hence the coarse-graining is not working at the high temperature range. Not only due to this matter, but also due to other factors as explained in the last paragraph of section ‘Results and Discussion’, we note that the framework is generally reliable only in the lower temperature range.
Equations for the self-diffusion coefficient
From the consequences of the previous subsections, Dε-Cu3Sn fully depends on DCu3Ti as follows:| | 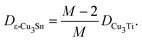 | (3) |
The ε-Cu3Sn phase is polycrystalline, where the grain boundaries face in different directions, so the ion diffusion in the phase should be isotropic. Thus, we evaluate DCu3Ti as an average of diffusion coefficients over the entire angle:| | | DCu3Ti = 1/3·(D(a) + D(c)). | (4) |
Here, D(a) [D(c)] is the diffusion coefficient of Cu ions along the a (c)-axis in the Cu3Ti-type structure.
The diffusion coefficient in a specific direction w (e.g. the a or c-axis) is given as
| |  | (5) |
Here,
Dj* is the contribution from ion jumps through route
j.
θj(
w) is the angle between the ion jump and direction
w. The projection of
Dj* is taken as squared cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θj
θj(
w), because
Dj* has dimensions of squared length. The contribution
Dj* is given as the following equation:
21(index
j omitted).
d is the distance of the diffusion route.
Cv is the vacancy formation rate given as a Boltzmann factor of the vacancy formation energy.
η is the jump rate, given as a product of a Boltzmann factor of the barrier energy and the vibration frequency. It is straightforward to calculate these quantities from
ab initio calculations. Computational details and results are given in Section 3. Meanwhile, it is difficult to perform an analytical evaluation of the correlation factor
f, which reflects the position exchanges sequentially occurring between the vacancy and the tracer ion: after an ion jump
via the vacancy, the vacancy is at the back of the tracer. Thus, the vacancy tends to pull back the tracer at the first position exchange in the reverse direction of the ion jump. Moreover, following the first one, position exchanges can occur again and again, which always move the tracer in the reverse direction of the preceding tracer move. The correlation factor
f represents how much the sequential exchanges affect the self-diffusion coefficient in total. Since the first exchange has the most significant contribution to the correlation factor, it must reduce
Dj* (
i.e. 0 ≤
f ≤ 1). It is tough to calculate this factor because we have to cover all of the vacancy tracks, which finally causes a position exchange between the vacancy and the tracer.
Now we return to the specific discussion on the Cu3Ti-type structure, consisting of routes a and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) . The contributions of ion jumps through both routes are denoted by Da,
. The contributions of ion jumps through both routes are denoted by Da,![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) *, respectively. According to eqn (5), the diffusion coefficients D(a) and D(c) are given as follows:
*, respectively. According to eqn (5), the diffusion coefficients D(a) and D(c) are given as follows:
| | D(a) = Da* + 2D![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) *cos2 *cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θa θa![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) , , | (7) |
In order to obtain Da,![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) * from eqn (6), we will deduce the correlation factors fa,
* from eqn (6), we will deduce the correlation factors fa,![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) . They are formally given as21
. They are formally given as21
| | 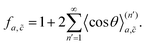 | (9) |
Here,
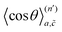
is an
n′th-order average cosine, which represents how much
n′ position exchanges between the vacancy and the tracer reduce the diffusion coefficient. The absolute value of

gradually decreases with
n′ increasing, so we should sum up just finite numbers of terms until the average cosine converges to zero. However, even for the coarse-grained diffusion network, it is not straightforward to evaluate
f because there are two kinds of diffusion routes
a and
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif)
: it is different how the next position exchange occurs depending on whether the tracer moved through route
a or
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif)
. Hence, we have to consider two patterns for every position exchange, so the number of patterns for
n′ exchanges increases in proportion to

. This complexity prevents one from evaluating the correlation factor for the multiple types of diffusion routes that there are. We thought of a way to extend the theory established for the case in which there are multiple types of diffusion routes, by taking a simultaneous recurrence formula: (i) in the case of
n′ = 1, the average cosine is given as
| | 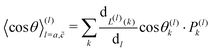 | (10) |
Here,

is the contribution of one position exchange between the tracer and the vacancy at site
k.
Pk is the probability that the position exchange occurs.
L(l)(
k) returns the type of route,
a or
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif)
, used for the position exchange. (ii) In the case of
n′ =
n + 1,
n + 1 position exchanges means that
n position exchanges occur after the first exchange through route
a or
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif)
. On the other hand, the contribution of the first exchange is weakened by the
nth order average cosine

. The above explanation is expressed as the following recurrence formula:
| |  | (11) |
In the ESI,† we provide detailed derivations to get P(l)k by counting up the probabilities of the hopping accompanied by a bit of complicated mathematical manipulation. From the derived P(l)k, we have evaluated  viaeqn (10) and (11), and hence the correlation factor fa,
viaeqn (10) and (11), and hence the correlation factor fa,![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) viaeqn (9). Then we can get the diffusion coefficient viaeqn (3)–(8).
viaeqn (9). Then we can get the diffusion coefficient viaeqn (3)–(8).
3 Computational details
We employed 2 × 2 × 2 supercells for both Cu3Ti-type and D019-type domains to reduce spurious interactions between two vacancies across the periodic boundaries. The lattice parameters are fixed at experimental values.18 We used VASP22 for the density functional calculation to evaluate the physical quantities. The barrier energies are evaluated with the climbing-nudged elastic band (c-NEB) method1 implemented in VASP.22 c-NEB needs the interpolated structures between both edges of the diffusion path as an input and optimizes them by connecting them by virtual ‘springs’. c-NEB guarantees that one of the structures is exactly positioned at the saddle point of the potential surface finally, in which c-NEB is superior to the original NEB method.23 We prepared 15 structures and set the spring coefficient as 5 eV Å−2. We used the PBE functional24 and PAW pseudopotentials provided in VASP25 for all of the calculations. The DFT energies are converged to better than 0.5 kJ per unit cell with respect to k-point sampling and plane wave cutoff energy. The vacancy formation energy is given as ΔEvac = Evac − Eperfect + μCu. Here, Eperfect is the total energy of a perfect crystal and Evac is that of a crystal including a vacancy defect. For the chemical potential of Cu ions, μCu, we evaluated it as the total energy per atom of a face-centered Cu mono-crystal. All Cu sites are equivalent, and their vacancy formation energy is given as 16.60 kJ mol−1. Meanwhile, the Cu3Ti-type domain has two distinguishable Cu sites, ‘top’ and ‘base’, and their vacancy formation energies are calculated as C(top)v = 25.94 kJ mol−1 and C(base)v = 21.71 kJ mol−1, respectively. We calculated the vibrational frequencies of tracer jumps with the harmonic approximation of the potential surface for ion jumps through every diffusion route: 1: 3.675 × 1012 s−1, 1′: 3.575 × 1012 s−1, 2: 4.152 × 1012 s−1, 3: 3.155 × 1012 s−1, 3′: 2.542 × 1012 s−1, 4: 4.138 × 1012 s−1, 5: 3.618 × 1012 s−1. (Vibrational frequencies of route 6 and 6′ are not calculated because they are already excluded from the diffusion network due to their high energy barriers.)
4 Results and discussion
Self-diffusion coefficient Dε-Cu3Sn calculated by our model is compared with experimental and classical MD values in Fig. 6. Our results reproduce experimental values reasonably: the predicted values pass through just the middle of the experimental values. The different periodicities, M = 4 (a in Fig. 6) and M = ∞ (b in Fig. 6), give twice different values. Meanwhile, the scatter of the experimental values (c–h in Fig. 6) is much larger, and the experimental discrepancy cannot be explained by the differences of periodicity M. The previous classical MD17 work (i in Fig. 6) overestimates our results and the average of experimental values by a digit, presumably due to using an empirical force-field. Another possible reason is that the time step used in the MD work is not small enough to evaluate the potential top of the diffusion route. (The time step is not shown in the MD paper.17) Nonetheless, this is unlikely to be true because the commonly used time step size is on the order of a few femtoseconds and it is much smaller than even the ion vibration frequencies shown in Section 3.
 |
| | Fig. 6 This work [a: M = 4, b: M = ∞]; experimental values [c: B. Chao et al.,11 d: B. Chao et al.,12 e: Y. Yang et al.,13 f: Y. Wang et al.,14 g: S. Kumar et al.,15 h: A. Paul et al.];16 classical MD [i: F. Gao and J. Qu].17 Comparison of the self-diffusion coefficient of Cu ions with an Arrhenius plot. The blue points represent our predictions with different periodicity M. The black and the red points represent the values reported from experiments and classical MD, respectively. | |
Fig. 7 shows the convergence of the correlation factors fa,![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) for the number of terms nmax to be summed in eqn (9). These graphs oscillate for small nmax because every position exchange somewhat counteracts the preceding tracer move: the first exchange counteracts the ion jump, and the second exchange similarly counteracts the ion move at the first exchange. Eventually, fa,
for the number of terms nmax to be summed in eqn (9). These graphs oscillate for small nmax because every position exchange somewhat counteracts the preceding tracer move: the first exchange counteracts the ion jump, and the second exchange similarly counteracts the ion move at the first exchange. Eventually, fa,![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) converge into constant values, and only they are needed to evaluate the model.
converge into constant values, and only they are needed to evaluate the model.
 |
| | Fig. 7 Convergence of correlation factor fa,![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) at 300, 500, and 800 K. This figure shows how the correlation factor fa, at 300, 500, and 800 K. This figure shows how the correlation factor fa,![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) converges with the number of pull-backs to be counted up increasing. The black dotted line is the reference value of the correlation factor, which is calculated for a 2-dimensional hexagonal lattice, nearly equaling 0.56.21 converges with the number of pull-backs to be counted up increasing. The black dotted line is the reference value of the correlation factor, which is calculated for a 2-dimensional hexagonal lattice, nearly equaling 0.56.21 | |
We verified the constructed model by confirming if the (converged) values of fa,![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) are reasonable by comparing them with a reference value: if route a and
are reasonable by comparing them with a reference value: if route a and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) were equivalent, the simplified diffusion network of the Cu3Ti-type structure would be regarded as an almost ideal 2-dimensional hexagonal lattice (see Fig. 5). Thus, it is interesting to compare fa,
were equivalent, the simplified diffusion network of the Cu3Ti-type structure would be regarded as an almost ideal 2-dimensional hexagonal lattice (see Fig. 5). Thus, it is interesting to compare fa,![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) with the correlation factor of the lattice, ∼0.56. First, in the case of low temperature (T = 300 K), fa is lower and f
with the correlation factor of the lattice, ∼0.56. First, in the case of low temperature (T = 300 K), fa is lower and f![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) is higher than 0.56, respectively. This comes from the fact that vacancies move through route l = a much more easily than through route l =
is higher than 0.56, respectively. This comes from the fact that vacancies move through route l = a much more easily than through route l = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) : the vacancy easily goes away from the tracer through route a after the tracer move (l =
: the vacancy easily goes away from the tracer through route a after the tracer move (l = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) ), so position exchanges seldom happen, and f
), so position exchanges seldom happen, and f![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) becomes higher. On the other hand, for the tracer move l = a, the vacancy moves through route a along the same line many times, so position exchanges frequently happen and fa becomes lower. In another way of thinking, the latter situation is similar to 1D diffusion so fa becomes much lower. Second, in the case of high temperature (T = 1000 K), it is expected that both fa and f
becomes higher. On the other hand, for the tracer move l = a, the vacancy moves through route a along the same line many times, so position exchanges frequently happen and fa becomes lower. In another way of thinking, the latter situation is similar to 1D diffusion so fa becomes much lower. Second, in the case of high temperature (T = 1000 K), it is expected that both fa and f![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) converge around 0.56 when the temperature increases. This is because routes a and
converge around 0.56 when the temperature increases. This is because routes a and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) are almost equivalent at high temperature, and the diffusion network is similar to an ideal 2D hexagonal lattice. The converged values are just 0.08 higher than 0.56. The small overestimation may be caused by the ignorance of vacancy tracks that include 3 routes or more. Nevertheless, the bias is quite small even at high temperature, compared to the dependence on periodicity M. Moreover, the bias is expected to get less at low temperature, because an infinite number of routes a is taken into consideration to count up vacancy tracks.
are almost equivalent at high temperature, and the diffusion network is similar to an ideal 2D hexagonal lattice. The converged values are just 0.08 higher than 0.56. The small overestimation may be caused by the ignorance of vacancy tracks that include 3 routes or more. Nevertheless, the bias is quite small even at high temperature, compared to the dependence on periodicity M. Moreover, the bias is expected to get less at low temperature, because an infinite number of routes a is taken into consideration to count up vacancy tracks.
In addition to the reason we described at the end of the subsection, ‘Coarse-graining’, there are several other factors which would limit the applicability of the present framework within the low temperature range: in our scheme, we have taken into account only the ‘barrier energies evaluated at zero temperature’ as the dominating factor in the ionic diffusion. At finite temperature, other possible factors would arise such as the change in the barrier energies due to anisotropic thermal expansion,26 interactions between point defects, and anharmonic effects.27 It is not practical to treat all these effects by extending the present ab initio based scheme. The present scheme would therefore be an appropriate approach within the low temperature range. Here we notice the complementary roles of the present strategy (for low temperature) and the MD-based one (high temperature). While the above ‘thermal effects’ could be captured well by the MD-based strategies, the slowing-down dynamics of the ionic jumps in the lower temperature range would be tough to capture by MD even with improved descriptions for longer time-scales such as the color-diffusion algorithm.28,29
5 Conclusions
We established a new modeling scheme to determine the ion self-diffusion coefficient, introducing some novel concepts. The scheme is applied to obtain the Cu self-diffusion coefficient in the ε-Cu3Sn phase of the Cu–Sn alloy in this work. The highlights of our scheme are ‘domain division’ and ‘coarse-graining’ of the diffusion network, based on barrier energies predicted by ab initio calculations. In the former concept, the diffusion network is divided into several types of disjunct domains. Then, the calculation for the original large unit cell is replaced by those for the different types of simple domains, which significantly reduces the calculation cost. The diffusion network of our target system, ε-Cu3Sn, is divided into two types of domains, which have 1- and 2-dimensional networks, respectively. In the latter concept, the diffusion networks of each domain are coarse-grained by merging some ion sites connected by routes having comparatively small energy barriers into just a single site (rep-site). This approximation is made on the grounds of the fact that the vacancy can move through these routes much more easily than through the others. As a result, it is established that the 1-dimensional domain never contributes to the self-diffusion21 and counting up of vacancy tracks in the 2D domain is much simplified. Finally, the established model successfully reproduces experimental values, better than previous classical MD work by a digit.17
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The computation in this work has been performed using the facilities of the Research Center for Advanced Computing Infrastructure (RCACI) at JAIST. T. I. is grateful for financial suport from a Grant-in-Aid for JSPS Research Fellow (18J12653). K. H. is grateful for financial support from a KAKENHI grant (JP17K17762), a Grant-in-Aid for Scientific Research on Innovative Areas “Mixed Anion” project (JP16H06439) from MEXT, PRESTO (JPMJPR16NA) and the Materials research by the Information Integration Initiative (MI2I) project of the Support Program for Starting Up Innovation Hub from Japan Science and Technology Agency (JST). R. M. is grateful for financial support from MEXT-KAKENHI (17H05478 and 16KK0097), from Toyota Motor Corporation, from I-O DATA Foundation, and from the Air Force Office of Scientific Research (AFOSR-AOARD/FA2386-17-1-4049). R. M. and K. H. are also grateful for financial support from MEXT-FLAGSHIP2020 (hp170269, hp170220).
Notes and references
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- W. Qiong, L. Shu-Suo, M. Yue and G. Sheng-Kai, Chin. Phys. B, 2012, 21, 109102 CrossRef.
- M. Mantina, Y. Wang, L. Chen, Z. Liu and C. Wolverton, Acta Mater., 2009, 57, 4102–4108 CrossRef CAS.
- M. Mantina, S. L. Shang, Y. Wang, L. Q. Chen and Z. K. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 184111 CrossRef.
- S. Huang, D. L. Worthington, M. Asta, V. Ozolins, G. Ghosh and P. K. Liaw, Acta Mater., 2010, 58, 1982–1993 CrossRef CAS.
- S. Choudhury, L. Barnard, J. Tucker, T. Allen, B. Wirth, M. Asta and D. Morgan, J. Nucl. Mater., 2011, 411, 1–14 CrossRef CAS.
- X. Zhang, H. Deng, S. Xiao, Z. Zhang, J. Tang, L. Deng and W. Hu, J. Alloys Compd., 2014, 588, 163–169 CrossRef CAS.
- A. D. Leclaire and A. B. Lidiard, Philos. Mag., 1956, 1, 518–527 CrossRef CAS.
- M. Koiwa and S. Ishioka, Philos. Mag. A, 1983, 48, 1–9 CrossRef CAS.
- M. Koiwa and S. Ishioka, J. Stat. Phys., 1983, 30, 477–485 CrossRef.
- B. Chao, S.-H. Chae, X. Zhang, K.-H. Lu, M. Ding, J. Im and P. S. Ho, J. Appl. Phys., 2006, 100, 084909 CrossRef.
- B. H.-L. Chao, X. Zhang, S.-H. Chae and P. S. Ho, Microelectron. Reliab., 2009, 49, 253–263 CrossRef.
- Y. Yang, Y. Li, H. Lu, C. Yu and J. Chen, Microelectron. Reliab., 2013, 53, 327–333 CrossRef CAS.
-
Y. Wang, S. H. Chae, J. Im and P. S. Ho, 2013 IEEE 63rd Electronic Components and Technology Conference, 2013, pp. 1953–1958.
- S. Kumar, C. A. Handwerker and M. A. Dayananda, J. Phase Equilib. Diffus., 2011, 32, 309–319 CrossRef CAS.
- A. Paul, C. Ghosh and W. J. Boettinger, Metall. Mater. Trans. A, 2011, 42, 952–963 CrossRef CAS.
- F. Gao and J. Qu, Mater. Lett., 2012, 73, 92–94 CrossRef CAS.
- M. Van Sande, R. De Ridder, G. Van Tendeloo, J. Van Landuyt and S. Amelinckx, Phys. Status Solidi A, 1978, 48, 383–394 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- X. Sang, K. Du and H. Ye, J. Alloys Compd., 2009, 469, 129–136 CrossRef CAS.
-
H. Mehrer, Diffusion in Solids: Fundamentals, Methods, Materials, Diffusion-Controlled Processes, Springer, Berlin, Heidelberg, 2007 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
-
H. Jónsson, G. Mills and K. W. Jacobsen, Nudged elastic band method for finding minimum energy paths of transitions, 1998, pp. 385–404 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- M. Mantina, Y. Wang, R. Arroyave, L. Q. Chen, Z. K. Liu and C. Wolverton, Phys. Rev. Lett., 2008, 100, 215901 CrossRef CAS PubMed.
- T. Indoh and M. Aniya, Phys. Res. Int., 2011, 2011, 1–3 CrossRef.
- P. C. Aeberhard, S. R. Williams, D. J. Evans, K. Refson and W. I. F. David, Phys. Rev. Lett., 2012, 108, 1–5 CrossRef PubMed.
- J. O. Nilsson, O. Y. Vekilova, O. Hellman, J. Klarbring, S. I. Simak and N. V. Skorodumova, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 1–7 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp06271d |
| ‡ When target ions are distributed nonuniformly in a crystal, their distribution changes macroscopically by thermal diffusion. This phenomena is called self-diffusion, and a measure of the speed is the self-diffusion coefficient. |
|
| This journal is © the Owner Societies 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Genki
Prayogo
b,
Kenta
Hongo
*a,
Genki
Prayogo
b,
Kenta
Hongo
 cdef and
Ryo
Maezono
af
cdef and
Ryo
Maezono
af
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, so the self-diffusion coefficient is given as a weighted average of those with their existence ratio:
2, so the self-diffusion coefficient is given as a weighted average of those with their existence ratio: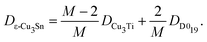


![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) , as shown in Fig. 5. (Route a is parallel to the a-axis but route
, as shown in Fig. 5. (Route a is parallel to the a-axis but route ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) deviates from the c-axis.) In this case, the diffusion coefficient DCu3Ti has a finite value.
deviates from the c-axis.) In this case, the diffusion coefficient DCu3Ti has a finite value.
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) and a respectively. Barrier energies of every route are listed below the figure. The diffusion network is partitioned by the thick zig-zag lines, because route 6, 6′ has much higher energy barriers than the others by >30 kJ mol−1. This picture is made using VESTA.19
and a respectively. Barrier energies of every route are listed below the figure. The diffusion network is partitioned by the thick zig-zag lines, because route 6, 6′ has much higher energy barriers than the others by >30 kJ mol−1. This picture is made using VESTA.19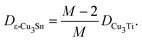

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θj(w), because Dj* has dimensions of squared length. The contribution Dj* is given as the following equation:21
θj(w), because Dj* has dimensions of squared length. The contribution Dj* is given as the following equation:21![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) . The contributions of ion jumps through both routes are denoted by Da,
. The contributions of ion jumps through both routes are denoted by Da,![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) *, respectively. According to eqn (5), the diffusion coefficients D(a) and D(c) are given as follows:
*, respectively. According to eqn (5), the diffusion coefficients D(a) and D(c) are given as follows:![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) *cos2
*cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θa
θa![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) ,
,![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) *cos2
*cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θc
θc![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif)
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) * from eqn (6), we will deduce the correlation factors fa,
* from eqn (6), we will deduce the correlation factors fa,![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) . They are formally given as21
. They are formally given as21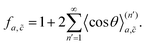
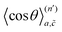 is an n′th-order average cosine, which represents how much n′ position exchanges between the vacancy and the tracer reduce the diffusion coefficient. The absolute value of
is an n′th-order average cosine, which represents how much n′ position exchanges between the vacancy and the tracer reduce the diffusion coefficient. The absolute value of  gradually decreases with n′ increasing, so we should sum up just finite numbers of terms until the average cosine converges to zero. However, even for the coarse-grained diffusion network, it is not straightforward to evaluate f because there are two kinds of diffusion routes a and
gradually decreases with n′ increasing, so we should sum up just finite numbers of terms until the average cosine converges to zero. However, even for the coarse-grained diffusion network, it is not straightforward to evaluate f because there are two kinds of diffusion routes a and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) : it is different how the next position exchange occurs depending on whether the tracer moved through route a or
: it is different how the next position exchange occurs depending on whether the tracer moved through route a or ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) . Hence, we have to consider two patterns for every position exchange, so the number of patterns for n′ exchanges increases in proportion to
. Hence, we have to consider two patterns for every position exchange, so the number of patterns for n′ exchanges increases in proportion to  . This complexity prevents one from evaluating the correlation factor for the multiple types of diffusion routes that there are. We thought of a way to extend the theory established for the case in which there are multiple types of diffusion routes, by taking a simultaneous recurrence formula: (i) in the case of n′ = 1, the average cosine is given as
. This complexity prevents one from evaluating the correlation factor for the multiple types of diffusion routes that there are. We thought of a way to extend the theory established for the case in which there are multiple types of diffusion routes, by taking a simultaneous recurrence formula: (i) in the case of n′ = 1, the average cosine is given as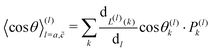
 is the contribution of one position exchange between the tracer and the vacancy at site k. Pk is the probability that the position exchange occurs. L(l)(k) returns the type of route, a or
is the contribution of one position exchange between the tracer and the vacancy at site k. Pk is the probability that the position exchange occurs. L(l)(k) returns the type of route, a or ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) , used for the position exchange. (ii) In the case of n′ = n + 1, n + 1 position exchanges means that n position exchanges occur after the first exchange through route a or
, used for the position exchange. (ii) In the case of n′ = n + 1, n + 1 position exchanges means that n position exchanges occur after the first exchange through route a or ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) . On the other hand, the contribution of the first exchange is weakened by the nth order average cosine
. On the other hand, the contribution of the first exchange is weakened by the nth order average cosine  . The above explanation is expressed as the following recurrence formula:
. The above explanation is expressed as the following recurrence formula:
 viaeqn (10) and (11), and hence the correlation factor fa,
viaeqn (10) and (11), and hence the correlation factor fa,![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) viaeqn (9). Then we can get the diffusion coefficient viaeqn (3)–(8).
viaeqn (9). Then we can get the diffusion coefficient viaeqn (3)–(8).
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) for the number of terms nmax to be summed in eqn (9). These graphs oscillate for small nmax because every position exchange somewhat counteracts the preceding tracer move: the first exchange counteracts the ion jump, and the second exchange similarly counteracts the ion move at the first exchange. Eventually, fa,
for the number of terms nmax to be summed in eqn (9). These graphs oscillate for small nmax because every position exchange somewhat counteracts the preceding tracer move: the first exchange counteracts the ion jump, and the second exchange similarly counteracts the ion move at the first exchange. Eventually, fa,![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) converge into constant values, and only they are needed to evaluate the model.
converge into constant values, and only they are needed to evaluate the model.
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) at 300, 500, and 800 K. This figure shows how the correlation factor fa,
at 300, 500, and 800 K. This figure shows how the correlation factor fa,![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) converges with the number of pull-backs to be counted up increasing. The black dotted line is the reference value of the correlation factor, which is calculated for a 2-dimensional hexagonal lattice, nearly equaling 0.56.21
converges with the number of pull-backs to be counted up increasing. The black dotted line is the reference value of the correlation factor, which is calculated for a 2-dimensional hexagonal lattice, nearly equaling 0.56.21![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) are reasonable by comparing them with a reference value: if route a and
are reasonable by comparing them with a reference value: if route a and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) were equivalent, the simplified diffusion network of the Cu3Ti-type structure would be regarded as an almost ideal 2-dimensional hexagonal lattice (see Fig. 5). Thus, it is interesting to compare fa,
were equivalent, the simplified diffusion network of the Cu3Ti-type structure would be regarded as an almost ideal 2-dimensional hexagonal lattice (see Fig. 5). Thus, it is interesting to compare fa,![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) with the correlation factor of the lattice, ∼0.56. First, in the case of low temperature (T = 300 K), fa is lower and f
with the correlation factor of the lattice, ∼0.56. First, in the case of low temperature (T = 300 K), fa is lower and f![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) is higher than 0.56, respectively. This comes from the fact that vacancies move through route l = a much more easily than through route l =
is higher than 0.56, respectively. This comes from the fact that vacancies move through route l = a much more easily than through route l = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) : the vacancy easily goes away from the tracer through route a after the tracer move (l =
: the vacancy easily goes away from the tracer through route a after the tracer move (l = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) ), so position exchanges seldom happen, and f
), so position exchanges seldom happen, and f![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) becomes higher. On the other hand, for the tracer move l = a, the vacancy moves through route a along the same line many times, so position exchanges frequently happen and fa becomes lower. In another way of thinking, the latter situation is similar to 1D diffusion so fa becomes much lower. Second, in the case of high temperature (T = 1000 K), it is expected that both fa and f
becomes higher. On the other hand, for the tracer move l = a, the vacancy moves through route a along the same line many times, so position exchanges frequently happen and fa becomes lower. In another way of thinking, the latter situation is similar to 1D diffusion so fa becomes much lower. Second, in the case of high temperature (T = 1000 K), it is expected that both fa and f![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) converge around 0.56 when the temperature increases. This is because routes a and
converge around 0.56 when the temperature increases. This is because routes a and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) are almost equivalent at high temperature, and the diffusion network is similar to an ideal 2D hexagonal lattice. The converged values are just 0.08 higher than 0.56. The small overestimation may be caused by the ignorance of vacancy tracks that include 3 routes or more. Nevertheless, the bias is quite small even at high temperature, compared to the dependence on periodicity M. Moreover, the bias is expected to get less at low temperature, because an infinite number of routes a is taken into consideration to count up vacancy tracks.
are almost equivalent at high temperature, and the diffusion network is similar to an ideal 2D hexagonal lattice. The converged values are just 0.08 higher than 0.56. The small overestimation may be caused by the ignorance of vacancy tracks that include 3 routes or more. Nevertheless, the bias is quite small even at high temperature, compared to the dependence on periodicity M. Moreover, the bias is expected to get less at low temperature, because an infinite number of routes a is taken into consideration to count up vacancy tracks.

