Electron transfer mediates vibrational relaxation of CO in collisions with Ag(111)

Abstract

We report experimental results on the state-to-state vibrational relaxation of CO(v = 17) in collisions with Ag(111) at incidence translational energies between 0.27 eV and 0.57 eV. These together with previous results provide a comprehensive set of data on two molecules (CO and NO)—one open and one closed shell—and two metals (Ag and Au). In all four cases, the incidence vibrational energy has been varied over several eV. We find a unifying relation between the probability of vibrational relaxation and the energetics of electron transfer from the metal to the molecule. This argues strongly that electronic friction based theories are not capable of explaining these data.

---

Introduction

Energy transfer from a solid metal's electron–hole pairs (EHPs) to a molecule's vibration was already evident when Rettner et al. showed that NO could become vibrationally excited in specular collisions with a hot Ag(111) surface even at low incidence translational energy¹—yet, the mechanism for this type of Born–Oppenheimer approximation² (BOA) failure in molecule–surface interactions remains a matter of debate.³ Since Rettner et al., vibrationally excited NO interacting with Au(111) has become a benchmark system for testing theoretical models beyond the Born–Oppenheimer approximation^3–12—these topics have been reviewed.^13–15 There is evidence that electron transfer (ET) forming a transient negative ion is a crucial part of the mechanism of BOA failure.^16,17 In this picture, electronic non-adiabaticity involves hops between a neutral and an anionic potential energy surface.¹⁸ An alternative explanation involves electronic friction on a single potential energy surface.^19,20

While these two theoretical models have similarities, they are derived using fundamentally different assumptions and describe physically different mechanisms. However, both theories fail to predict the correct amount of vibrational energy transferred to the surface and the incidence translational energy dependence of the vibrational relaxation probability. Since neither has succeeded in accounting for experimental observation, it is difficult to assess the validity of electronic friction versus surface hopping (ET).^6,7 In this work, we show measurements that qualitatively distinguish between these two mechanisms without making quantitative comparisons to theory.

If electron transfer initiates BOA failure, the surface work function, Φ, and the molecule's ability to bind an electron determine the energetics of the BOA failure. The work function and the molecule's electron binding energy define the energy by which the molecule's affinity level needs to be stabilized such that the anionic and the neutral diabats cross and the ET becomes energetically feasible. Scattering experiments in which the surface work function and the molecule's electron binding energy are systematically varied allow the comparison of conditions that sample the ET curve crossing to those that do not. This requires a set of data for more than one molecule (variation of electron binding energy) and more than one surface (variation of work function).

Of course, the crossing is actually a seam in a high dimensional space and it depends strongly on the molecule's distance from the surface and its vibrational coordinate. Hence, we choose molecules whose incidence vibrational and translational energy can be varied over as wide a range as possible.

NO is an ideal choice. Forming molecular beams of NO is a convenient way to control incidence translational energy. For controlling vibrational excitation, infrared overtone pumping^4,5 and stimulated emission pumping²¹ (SEP) are both possible.^22–26 Furthermore, background produced by competing spontaneous emission can be reduced.²⁷

CO is our second molecule. Forming CO molecular beams is straightforward as is overtone pumping.^28,29 Unfortunately, for CO, SEP requires complex light sources in the vacuum UV making its implementation more difficult than for NO. Nevertheless, it is now possible to produce CO(v = 17) by the newly developed PUMP-PUMP-PERTURB-DUMP (P³D)³⁰ approach, which we will describe below.

To vary the work function of the solid we chose two similar metals, Ag(111) (Φ = 4.7 eV) and Au(111) (Φ = 5.3 eV). NO and CO interact weakly with both metals, the metals’ electronic structures are similar, and even their lattice constants are similar. For NO(v), vibrational inelasticity has been studied on Au(111) and Ag(111)—the vibrational relaxation probability of highly vibrationally excited NO is significantly higher at Ag(111) (Φ = 4.7 eV) than at Au(111) (Φ = 5.3 eV).³¹ Furthermore, varying the thickness of atomically defined Ag thin films on Au(111) showed a clear correlation between vibrational relaxation probability and surface work function.³²

We have also employed P³D to study scattering of CO(v = 17) from Au(111).³³ The final vibrational state distribution indicates significantly less vibrational relaxation than is observed for NO scattered from Au(111). This observation is expected for an ET mediated process considering the reduced electron affinity of CO (E_A = −1.5 eV) compared to NO (E_A = 0.03 eV).

Table 1 displays previously investigated systems of highly vibrationally excited molecules scattered from metal surfaces. The molecule's electron affinity and the metal's work function exert a strong influence on the relaxation probability.

Table 1 Investigated combinations of highly vibrationally excited diatomic molecules and metal surfaces. The vibrational relaxation probability depends on the molecule's electron affinity and the metal's work function

	Work function: high (Φ = 5.3 eV)	Work function: low (Φ = 4.7 eV)
Electron affinity: high (EA = 0.03 eV)	NO(v = 11)/Au(111)^12	NO(v = 11)/Ag(111)^31
	Medium vibrational relaxation	Strong vibrational relaxation
Electron affinity: low (EA = −1.5 eV)	CO(v = 17)/Au(111)^33	CO(v = 17)/Ag(111)
	Weak vibrational relaxation	This work
		Medium vibrational relaxation

---

In this work, we complete a minimal data set needed to investigate the influence of electron affinity and work function by reporting experiments on the scattering of highly vibrationally excited CO(v = 17) from Ag(111). As expected for an ET mediated interaction, we observe more efficient vibrational relaxation compared to scattering of CO(v = 17) from Au(111). Combining all available data, we also find a unifying relation between the probability of vibrational relaxation and the energetics of electron transfer from the metal to the molecule.

Experimental

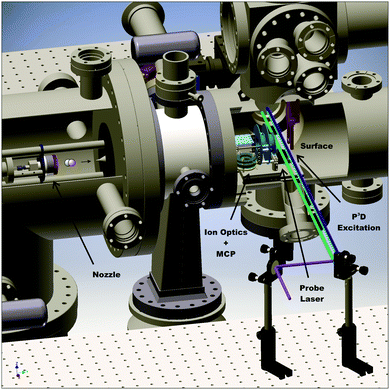
Fig. 1 depicts the experimental apparatus used in this work. A pulsed supersonic expansion of CO is produced using a home-built nozzle. After passing through a differentially pumped chamber, the beam enters the scattering chamber maintained near 10⁻¹⁰ Torr. We tune the incidence translational energy of the molecular beam between 0.27 eV and 0.57 eV by seeding different amounts of CO in H₂ carrier gas. We clean Ag(111) (MaTecK, 99.999% purity) by Ar-ion sputtering (LK Technologies, NGI 3000, 3 kV, 20 mA emission current, 12 μA surface current, 20 min) and subsequent annealing (870 K, 20 min). The cleanliness of the surface is probed by Auger electron spectroscopy (ESA-150, Staib Instruments). No chemical impurities can be found on the surface after 9 h exposure to the molecular beam. Scattering experiments using Ag(111) are performed at a surface temperature of 400 K; for experiments using a chlorinated silver surface, the temperature was 300 K. The chlorinated Ag(111) surface was prepared by leaking molecular chlorine into the chamber. The clean surface was exposed to a pressure of 5 × 10⁻⁸ Torr Cl₂ for 5 min. Following the procedure by Wu et al., the chlorine Auger signal was monitored in order to ensure that the dosed amount of chlorine leads to the desired increase of the work function by 1.5 eV.³⁴

Fig. 1 Experimental setup for CO(v = 17) scattering from Ag(111). The molecular beam is produced using a supersonic expansion in a home-built nozzle (left). After passing a skimmer and a differential pumping chamber, it collides with the surface mounted in the ultra-high vacuum (UHV) chamber. Prior to the surface collision, CO molecules are vibrationally excited to v = 17 employing the P³D excitation scheme (blue, light blue, and purple laser pulses in the sketch). Scattered molecules are then ionized by the probe laser (green). Ions are guided by ion optics (turquoise) to the multi-channel plate (MCP, dark green), also mounted in the UHV chamber.

Highly vibrationally excited CO is produced by the PUMP-PUMP-PERTURB-DUMP (P³D) method.³⁰ First, a laser pulse (PUMP 1) transfers CO molecules from the ground state X¹Σ⁺(v = 0) to the first electronically excited triplet state a³Π(v = 0) using 1 mJ of 206.29 nm laser radiation generated by mixing the fourth harmonic of a Nd:YAG laser (Lab 170-10, Spectra Physics) with the output of a home-built narrow-band injection seeded optical parametric oscillator (OPO), pumped by the second harmonic of the same Nd:YAG laser.³⁵ In a second step (PUMP 2), we excite the e³Σ⁻(v = 12) ← a³Π(v = 0) transition using a 2.0 mJ pulse at 368.86 nm produced by the frequency doubled output of a dye laser (Spectra Physics PDL-2, Styryl 8 (LDS 751) by Exciton), pumped by the second harmonic of a Nd:YAG laser (Continuum Powerlite 9010). A perturbation between e³Σ⁻(v = 12, J = 1) and A¹Π(v = 8, J = 1) (PERTURB) lends oscillator strength to the normally forbidden stimulated emission (DUMP) transitions to the X¹Σ⁺(v = 17) level. For the DUMP step, we use the frequency doubled output of a dye laser (Sirah Stretch, Coumarin C480), pumped by the third harmonic of a Nd:YAG laser (Continuum Powerlite 9010) to generate 2.4 mJ per pulse at 234.16 nm.

We detect scattered CO molecules in X¹Σ⁺(14 ≤ v_f ≤ 18) using (1 + 1) A¹Π(v′, J′) ← X¹Σ⁺(v′′, J′′) REMPI detection covering the wavelength range 228–245 nm with the frequency doubled output of a dye laser (Sirah Precision Scan, Coumarin C480), pumped by the third harmonic of a Nd:YAG laser (Spectra Physics Lab 230-10). Ions are detected on multi-channel plates (MCP, tectra, chevron configuration, 25 mm diameter). The signal is recorded at an oscilloscope (LeCroy, Waverunner LT344), which is connected to a personal computer (PC).

We record REMPI spectra both with the DUMP laser turned on and turned off. When the DUMP laser is turned off, CO molecules in X¹Σ⁺(14 ≤ v_f ≤ 18) are produced by spontaneous fluorescence and inelastic scattering. When the DUMP laser is turned on, differences in signals result directly from the enhanced population of X¹Σ⁺(v = 17, J = 0). Thus the DUMP-off spectrum is a background that is subtracted in the data analysis.

Results

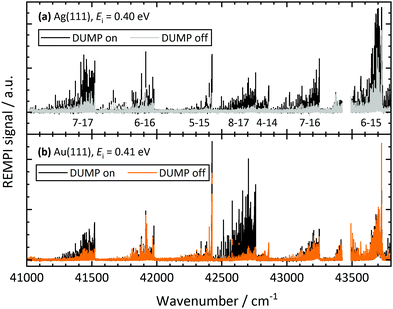
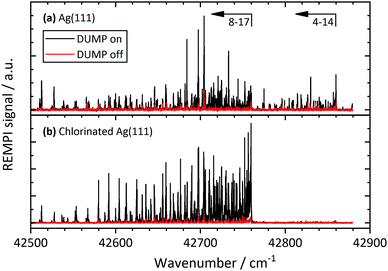
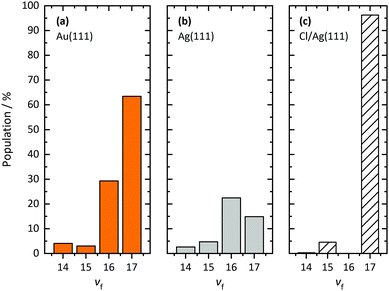
Fig. 2 shows REMPI spectra of scattered CO after CO(v = 17) collides with Ag(111) and Au(111), in both cases at an incidence translational energy of 0.4 eV. Vibrational bands are well resolved and can easily be assigned. The difference in the band intensity when the DUMP laser is on versus off indicates population in final vibrational states due to incident CO(v = 17). It is obvious that the relaxation probability of CO(v = 17) is higher for collisions with Ag(111) than for collisions with Au(111). For Au, only bands probing the prepared state (8-17 and 7-17) increase in intensity with the DUMP laser turned on, whereas for Ag, every band in the spectrum increases.

Fig. 2 REMPI spectra of CO(v = 17) scattered from Ag(111) and Au(111) at incidence translational energies of 0.4 eV. For each surface, the spectrum has been recorded with the DUMP laser on and off. This way, the background induced by fluorescence can be determined. Vibrational relaxation caused by CO(v = 17) scattering can be estimated based on the different band intensities for DUMP laser on versus DUMP laser off. Vibrational bands are denoted by v′–v′′, where v′ is the vibrational state in the A¹Π state and v′′ is the vibrational state in the electronic ground state. It is obvious that most population stays in v = 17 when scattering CO(v = 17) from a Au(111) surface. See panel (b). In contrast, vibrational bands corresponding to lower vibrational states gain intensity when scattering from a Ag(111) surface. See panel (a).

Fig. 3 shows the effect of surface chlorination on the scattering of incident CO(v = 17). Here, the work function is 6.2 eV and the vibrational relaxation probability is greatly reduced. We have used scattering from this surface as a convenient control—i.e. relaxation probability is close to zero—to derive absolute relaxation probabilities under other conditions by comparison of relative signal intensities. See ESI.†

Fig. 3 Panel (a): REMPI spectra of CO(v = 17) scattered from a clean Ag(111) surface in the frequency range of the 8–17 and 4–14 vibrational bands for E_i = 0.57 eV. Spectra are shown for DUMP laser on (black) and DUMP laser off (red). Panel (b): Spectra in the same frequency range for a chlorinated Ag(111) surface which exhibits a significantly larger work function. Hence, vibrational relaxation is drastically reduced and only enhancement of the 8–17 band is observed when the DUMP laser is turned on.

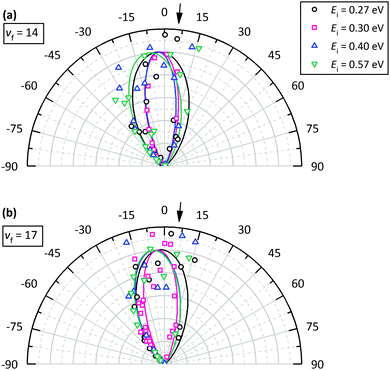
Fig. 4 shows angular distributions of state selected scattered molecules. The angular distributions are all narrow, indicating a direct scattering process. Furthermore, the final rotational energy of rotationally-inelastically scattered molecules and the final translational energy of rotationally- and vibrationally-elastically scattered molecules increase with incidence translational energy. These observations strongly suggest a direct scattering mechanism; a trapping-and-desorption mechanism is excluded for all presented results.

Fig. 4 Panel (a): Angular distributions of CO(v_i = 17 → v_f = 14) scattering at Ag(111). Panel (b): Angular distributions of CO(v_i = 17 → v_f = 17) scattering at Ag(111). All angular distributions are narrow indicating a direct scattering process. The arrows in the figure display the angle of the incident beam, which is 5° due to experimental limitations.

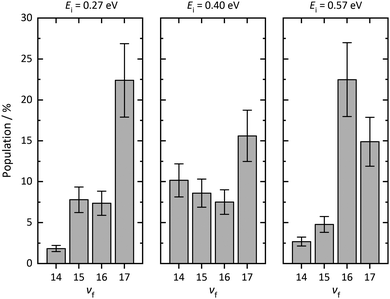
Using REMPI spectra and angular distributions like those mentioned above, we derive the vibrational state scattering distributions. See ESI† for detailed information about the analysis method. Fig. 5 displays the calculated distributions for incident CO(v = 17) scattered from three surfaces: Au(111), Ag(111), and chlorinated Ag(111) at E_i = 0.57 eV. Whereas vibrational relaxation is close to absent on the chlorinated surface, it is stronger on Au(111) and strongest on Ag(111). For Au(111)³³ and chlorinated Ag(111), all molecules scatter into v ≥ 14. For Ag(111), about 60% of scattered CO molecules populate vibrational states below v = 14. Vibrational excitation is not observed in any case.

Fig. 5 Final vibrational state distributions of CO(v = 17) scattered from Au(111), Ag(111), and chlorinated Ag(111) at E_i = 0.57 eV. The distributions have been calculated based on the REMPI spectra shown in Fig. 2 and 3. The distributions show populations in % for each final vibrational state, v_f. In contrast to Au(111), we observe little population of vibrational states between v_f = 14 and v_f = 17 for scattering from Ag(111). Note that the employed REMPI scheme only detects molecules between v = 14 and v = 17. For Ag(111), a large fraction of CO molecules undergo vibrational relaxation to states below v_f = 14. For scattering from chlorinated Ag(111), more than 95% of the molecules stay in the initial vibrational state.

Fig. 6 displays the incidence translational energy dependence of the vibrational state scattering distributions for CO(v = 17) scattered from Ag(111). The survival probability of the incident vibrational state decreases with increasing incidence translational energy.

Fig. 6 Final vibrational state distributions for CO(v = 17) scattered from Ag(111) at different incidence translational energies E_i. The incidence vibrational state survival probability of CO(v = 17) decreases at elevated translational energies.

Discussion

The strategy taken in this work is to aggregate data from multiple scattering systems for which the molecules’ electron binding energies and the solids’ work functions are varied. Fig. 7 provides an overview of different molecule–surface systems and different initial vibrational excitations. Here, relaxation probability is plotted versus incidence translational energy both at low and high incidence vibrational excitation. While the vibrational relaxation probability obviously depends on incidence translational energy, the ordering of the six data sets (from low to high probability) does not.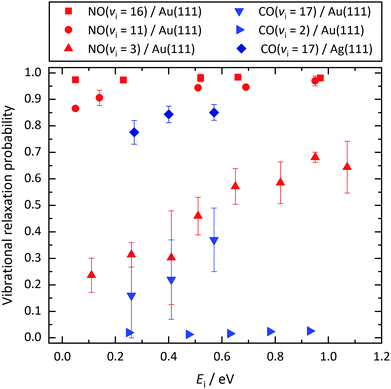

Fig. 7 Vibrational relaxation probabilities of diatomic molecules initially prepared in different vibrationally excited states v_i as a function of incidence translational energy E_i. Results obtained for CO(v_i = 17)/Ag(111) are compared to results previously published for NO(v_i = 3, 11, 16)/Au(111),¹² CO(v_i = 2)/Au(111),¹¹ and CO(v_i = 17)/Au(111).³³ For both CO and NO, the relaxation probability increases with v_i. For similar v_i, the NO relaxation probability is larger than that of CO. Molecule–surface systems with a relaxation probability between 0 and 1 exhibit a pronounced dependence on E_i.

The relaxation probability is very sensitive to the initial vibrational excitation because the effective electron affinity depends on the vibrational state. This is due to the fact that the seam of crossing to the anionic potential energy surface is located at diatomic bond lengths greater than the corresponding neutral molecule's equilibrium bond length. Therefore, we introduce the vertical electron binding energy, E_v(r_out), the energy difference between the neutral and anionic molecules at the outer classical turning point, r_out, of a specific vibrational state, v. The difference between this and the work function, E_v(r_out) − Φ, describes the energy needed to transfer an electron from the metal to the molecule when the molecule is still far from the surface.

Fig. 8(a) shows this is a useful indicator of the likelihood of vibrational relaxation. Here, we plot vibrational relaxation probability versus E_v(r_out) − Φ for several scattering experiments. The graph includes different surfaces, different molecules, and different initial vibrational states. All these systems follow a common trend, showing an increase of the relaxation probability from 0 to 1 between E_v(r_out) − Φ = −5.25 and −3.5 eV.

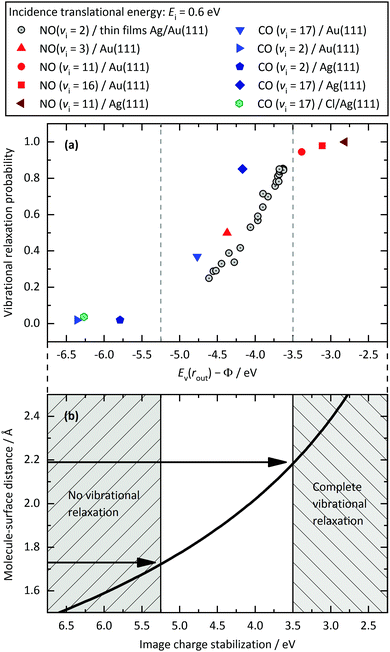Fig. 8 Panel (a): Relaxation probability of various molecule–surface systems as a function of E_v(r_out) − Φ at an incidence translational energy of 0.6 eV. In addition to CO(v_i = 17)/Ag(111), results are shown for CO(v_i = 17)/Au(111),³³ CO(v_i = 2)/Ag(111),³² CO(v_i = 2)/Au(111),¹¹ NO(v_i = 11)/Ag(111),³¹ NO(v_i = 3, 11, 16)/Au(111),¹² and NO(v_i = 2) on thin films of Ag on Au(111).³² All systems follow a common trend showing an increase of the relaxation probability from 0 to 1 between −5.25 eV and −3.5 eV. Panel (b): Image charge stabilization (ICS) of a negatively charged molecule in the vicinity of the surface. The ICS must compensate for the difference E_v(r_out) − Φ to make the ET energetically feasible. Values below −5.25 eV cannot be achieved by ICS as the molecule cannot get closer to the surface and approaches the repulsive wall at which it is scattered back. Therefore, the molecule does not reach the region of non-adiabatic interactions and no vibrational relaxation occurs. For values above −3.5 eV, the molecule remains long enough in regions of electronic non-adiabaticity so that complete vibrational relaxation occurs. The arrows indicate corresponding molecule–surface distances.

This trend reflects the distance of the molecule from the surface when ET occurs, as image charge interaction stabilizes the anion closer to the surface.³³Fig. 8(b) shows the image charge stabilization (ICS) as a function of distance from the surface. The ICS is computed by using eqn (1) of ref. 36. The onset of vibrational relaxation occurs for an E_v(r_out) − Φ ∼ −5.25 eV—ICS of this magnitude requires a close approach of 1.75 Å. When E_v(r_out) − Φ ∼ −3.5 eV, the required ICS is smaller, and the molecule need only approach to within 2.2 Å to reach the curve crossing for ET. Hence, the distance of the molecule's closest approach appears to be in the region of 1.75 and 2.2 Å—these values agree well with DFT calculations for the repulsive wall which give 1.9 Å for CO/Au(111),³³ 2.0 Å for NO/Au(111),³³ 2.2 Å for CO/Ag(111),³⁷ and 1.9 Å for NO/Ag(111).³⁷ Here, we estimate the position of the repulsive wall by calculating the molecule–surface distance at which the interaction energy reaches a value of 0.5 eV.

Thus it is easy to understand why the curve of Fig. 8(a) appears as it does—ICS can easily compensate E_v(r_out) − Φ = −3.5 eV at reasonably large distances from the surface. However, if E_v(r_out) − Φ ≲ −5.25 eV, the molecule cannot approach the surface closely enough to compensate this energy gap before encountering the repulsive part of the potential.

In the intermediate regime where E_v(r_out) − Φ is between −3.5 eV and −5.25 eV, the relaxation probability varies between 0 and 1. Notice that in the intermediate case, we observe a strong dependence on E_i. See Fig. 7. For these systems, the relaxation probability critically depends on the closest approach of the molecule to the surface and the resultant ICS. Increased E_i allows closer approach to the curve crossing, resulting in increased relaxation probability.

Conclusions

The aggregated results presented here show that the vibrational relaxation probability for CO and NO scattering from Au or Ag can be predicted knowing only the solid's work function and the molecule's vibrational state specific vertical electron binding energy. This strongly argues that electron transfer involving surface hopping governs the electronically non-adiabatic vibrational energy transfer in these systems.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge support by the Alexander von Humboldt Foundation. T. S. acknowledges financial support by the Deutsche Forschungsgemeinschaft under grant SCHA 1946/2-1. R. J. V. W. gratefully acknowledges a PhD fellowship granted by the Fonds der Chemischen Industrie.

Notes and references

1. C. T. Rettner, F. Fabre, J. Kimman and D. J. Auerbach, Phys. Rev. Lett., 1985, 55, 1904–1907.
2. M. Born and R. Oppenheimer, Ann. Phys., 1927, 84, 0457–0484.
3. R. Cooper, C. Bartels, A. Kandratsenka, I. Rahinov, N. Shenvi, K. Golibrzuch, Z. Li, D. J. Auerbach, J. C. Tully and A. M. Wodtke, Angew. Chem., Int. Ed., 2012, 51, 4954–4958.
4. N. Bartels, K. Golibrzuch, C. Bartels, L. Chen, D. J. Auerbach, A. M. Wodtke and T. Schäfer, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 17738–17743.
5. K. Golibrzuch, P. R. Shirhatti, J. Altschäffel, I. Rahinov, D. J. Auerbach, A. M. Wodtke and C. Bartels, J. Phys. Chem. A, 2013, 117, 8750–8760.
6. K. Golibrzuch, P. R. Shirhatti, I. Rahinov, A. Kandratsenka, D. J. Auerbach, A. M. Wodtke and C. Bartels, J. Chem. Phys., 2014, 140, 044701.
7. B. C. Krüger, N. Bartels, C. Bartels, A. Kandratsenka, J. C. Tully, A. M. Wodtke and T. Schäfer, J. Phys. Chem. C, 2015, 119, 3268–3272.
8. N. Bartels, K. Golibrzuch, C. Bartels, L. Chen, D. J. Auerbach, A. M. Wodtke and T. Schäfer, J. Chem. Phys., 2014, 140, 054710.
9. K. Golibrzuch, A. Kandratsenka, I. Rahinov, R. Cooper, D. J. Auerbach, A. M. Wodtke and C. Bartels, J. Phys. Chem. A, 2013, 117, 7091–7101.
10. B. C. Krüger, N. Bartels, A. M. Wodtke and T. Schäfer, Phys. Chem. Chem. Phys., 2016, 18, 14976–14979.
11. K. Golibrzuch, PhD thesis, Georg-August-Universität Göttingen, 2014.
12. N. Bartels, B. C. Krüger, D. J. Auerbach, A. M. Wodtke and T. Schäfer, Angew. Chem., Int. Ed., 2014, 53, 13690–13694.
13. A. M. Wodtke, D. Matsiev and D. J. Auerbach, Prog. Surf. Sci., 2008, 83, 167–214.
14. A. M. Wodtke, Chem. Soc. Rev., 2016, 45, 3641–3657.
15. K. Golibrzuch, N. Bartels, D. J. Auerbach and A. M. Wodtke, Annu. Rev. Phys. Chem., 2015, 66, 399–425.
16. Y. H. Huang, C. T. Rettner, D. J. Auerbach and A. M. Wodtke, Science, 2000, 290, 111–114.
17. J. W. Gadzuk, J. Chem. Phys., 1983, 79, 6341–6348.
18. N. Shenvi, S. Roy and J. C. Tully, J. Chem. Phys., 2009, 130, 174107.
19. M. Head-Gordon and J. C. Tully, J. Chem. Phys., 1995, 103, 10137–10145.
20. S. Monturet and P. Saalfrank, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 075404.
21. C. Kittrell, E. Abramson, J. L. Kinsey, S. A. McDonald, D. E. Reisner, R. W. Field and D. H. Katayama, J. Chem. Phys., 1981, 75, 2056–2059.
22. X. M. Yang, E. H. Kim and A. M. Wodtke, J. Chem. Phys., 1990, 93, 4483–4484.
23. X. M. Yang, E. H. Kim and A. M. Wodtke, J. Chem. Phys., 1992, 96, 5111–5122.
24. X. M. Yang and A. M. Wodtke, J. Chem. Phys., 1992, 96, 5123–5128.
25. X. M. Yang and A. M. Wodtke, Int. Rev. Phys. Chem., 1993, 12, 123–147.
26. M. Silva, R. Jongma, R. W. Field and A. M. Wodtke, Annu. Rev. Phys. Chem., 2001, 52, 811–852.
27. N. Bartels, B. C. Krüger, S. Meyer, A. M. Wodtke and T. Schäfer, J. Phys. Chem. Lett., 2013, 4, 2367–2370.
28. K. Golibrzuch, P. R. Shirhatti, J. Geweke, J. Werdecker, A. Kandratsenka, D. J. Auerbach, A. M. Wodtke and C. Bartels, J. Am. Chem. Soc., 2015, 137, 1465–1475.
29. P. R. Shirhatti, I. Rahinov, K. Golibrzuch, J. Werdecker, J. Geweke, J. Altschäffel, S. Kumar, D. J. Auerbach, C. Bartels and A. M. Wodtke, Nat. Chem., 2018, 10, 592–598.
30. N. Bartels, T. Schäfer, J. Hühnert, R. W. Field and A. M. Wodtke, J. Chem. Phys., 2012, 136, 214201.
31. B. C. Krüger, S. Meyer, A. Kandratsenka, A. M. Wodtke and T. Schäfer, J. Phys. Chem. Lett., 2016, 7, 441–446.
32. C. Steinsiek, P. R. Shirhatti, J. Geweke, C. Bartels and A. M. Wodtke, J. Phys. Chem. C, 2018, 122, 10027–10033.
33. R. J. V. Wagner, N. Henning, B. C. Krüger, G. B. Park, J. Altschäffel, A. Kandratsenka, A. M. Wodtke and T. Schäfer, J. Phys. Chem. Lett., 2017, 8, 4887–4892.
34. K. Wu, D. Wang, J. Deng, X. Wei, Y. Cao, M. Zei, R. Zhai and X. Guo, Surf. Sci., 1992, 264, 249–259.
35. L. Velarde, D. P. Engelhart, D. Matsiev, J. LaRue, D. J. Auerbach and A. M. Wodtke, Rev. Sci. Instrum., 2010, 81, 063106.
36. N. V. Smith, C. T. Chen and M. Weinert, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 7565–7573.
37. A. Kandratsenka and J. Altschäffel, Personal communication, Department of Dynamics at Surfaces, Max-Planck-Institute for Biophysical Chemistry, Am Faßberg 11, 37077 Goettingen, Germany, 2018.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp06041j

---