Structural isomers and low-lying electronic states of gas-phase M⁺(N₂O)_n (M = Co, Rh, Ir) ion–molecule complexes

Abstract

The structures of gas-phase group nine cation–nitrous oxide metal–ligand complexes, M⁺(N₂O)_n (M = Co, Rh, Ir; n = 2–7) have been determined by a combination of infrared photodissociation spectroscopy and density functional theory. The infrared spectra were recorded in the region of the N₂O asymmetric (N=N) stretch using the inert messenger technique and show spectroscopically distinct features for N- and O-bound isomers. The evolution of the spectra with increasing ligand number is qualitatively different for each of the metal ions studied here with only Co⁺(N₂O)_n complexes behaving similarly to the coinage metal complexes studied previously. The rich variety of electronic and isomeric structures identified make these species attractive targets for infrared-driven, isomer selective intra-complex chemistry.

---

1. Introduction

Accounting for 5% of anthropogenic greenhouse emissions, nitrous oxide (N₂O) is a potent greenhouse gas^1,2 with a warming potential 300 times greater than carbon dioxide. In addition to its climate change potential, as the primary source of stratospheric NO_x, surface N₂O emissions represent the dominant ozone-depleting emissions of the 21st century.^1,2 Human actions such as manufacturing, fossil fuel use, and agriculture have given rise to increased emissions and N₂O concentrations are rising by 0.5–0.9 ppb per volume per year.³

Although unregulated by the Montreal Protocol,⁴ as a result of its negative environmental impact there is considerable interest in reducing N₂O emissions. One effective route to reducing emissions is via metal-catalysed N₂O reduction^5,6 and this has been an active area of research in conventional heterogeneous catalysis and cluster science.⁷

At the very simplest level, the reactions of atomic transition metal cations and N₂O have been studied in detail by Böhme and coworkers,⁸ and the role of atomic and cluster ions as the ultimate single-site catalysts has been reviewed by Böhme and Schwarz.³ In terms of reactions of N₂O with metal ions, M^+/0/−(N₂O)_n complexes represent model entrance-channel species in which the fundamental interactions can be studied in isolation.⁹ Metal atom–N₂O binding has been studied both theoretically^10–12 and experimentally,^13,14 and the reactions of nitrous oxide with charged metal clusters have received much attention both under thermal and single-collision conditions.^15–23

We recently reported a spectroscopic study of M⁺(N₂O)_n (M = Cu, Ag, Au) complexes in which infrared photodissociation (IRPD) spectroscopy was combined with quantum chemical calculations to identify common structural binding motifs.²⁴ Spectroscopically distinct nitrogen- and oxygen-bound ligands were identified giving rise to a rich diversity of structural isomers. However, in practical NO_x-reduction catalysis, it is not the coinage metals which are typically used but the platinum group metals. Rhodium in particular plays a prominent role in the N₂O reduction in the automobile three-way catalytic converter. This in turn led to many fundamental studies of rhodium cluster reactions with nitrogen oxides,^19,25–30 including infrared-driven cluster surface reactions.^31–33

Here, we report a combined experimental and quantum chemical study of group 9 ion –N₂O complexes, M⁺(N₂O)_n (M = Co, Rh, Ir) with the aim of investigating the fundamental interactions involved in the early stages of nitrous oxide reduction at heterogeneous catalysts. IRPD spectroscopy, using the Ar-tagging technique has been applied to determine the structures of the title complexes by comparison with the simulated spectra of energetically low-lying electronic and/or isomeric forms determined from density functional theory (DFT). This powerful approach has been employed by several groups, including our own, to provide reliable information on the structures of many gas-phase metal–ligand complexes^34–36 including, recently, those of metal–nitrosyl complexes M⁺(NO)_n.^37,38

2. Experimental

The instrument and technique employed in these studies have been described previously^24,39 and only brief details are given here. Gas-phase M⁺(N₂O)_n (M = Co, Rh, Ir) complexes and their argon-tagged counterparts are formed by entraining the products of focussed 532 nm pulsed laser ablation of a rotating metal disc in a 6 bar pulse of Argon carrier gas seeded with 0.6% N₂O. As the gas expands into high vacuum weakly-bound complexes are formed in many-body collisions and subsequently cooled in the ensuing expansion. The resulting molecular beam is skimmed and the positively-charged species are detected by reflectron time-of-flight mass spectrometry.⁴⁰ The cluster source and detection operates at 10 Hz.

Infrared spectra of the complexes of interest are recorded using the inert messenger technique^41–46 – in this case using weakly-bound Ar atoms. Pulsed infrared radiation, tuneable in the region of the fundamental of the ν₃ asymmetric (N=N) stretch of nitrous oxide 2150–2400 cm⁻¹, is provided by an optical parametric oscillator/amplifier system (LaserVision). The infrared beam counter-propagates with the molecular beam and operates on a three pulse on/three pulse off duty cycle, allowing continuous IR on–off subtraction (total of 300 laser shots at each point). Absorption of an infrared photon results in heating of the complex and detachment of the weakly-bound Ar atom which thus provides a mass spectrometric signature. Monitoring the fractional depletion of the M⁺(N₂O)_n–Ar complex as a function of wavenumber yields the infrared spectrum of the M⁺(N₂O)_n complex of interest.

To aid in assigning and interpreting the experimental data, the structures and simulated infrared spectra of energetically low-lying isomers were calculated using density functional theory (DFT) employing the B3P86 hybrid density functional⁴⁷ coupled with the Def2TZVP basis set.^48,49 All calculations were carried out using the Gaussian09 suite of programs.⁵⁰ To aid comparison with experimental spectra, the wavenumbers of infrared bands in the calculated spectra have been scaled by a factor 0.932, derived from the calculated ν₃ stretch of free N₂O.⁵¹ Further details of the calculations, including structures of all isomers together with composite simulated spectra can be found in the ESI.†

3. Results and discussion

3.1 M⁺(N₂O)_n–Ar spectra

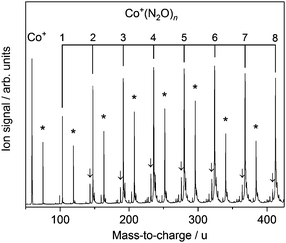
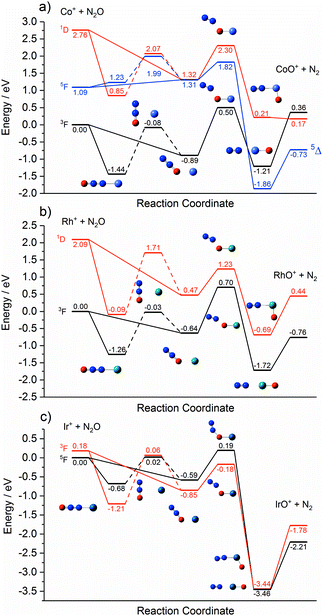
Fig. 1 shows the time-of-flight mass spectrum illustrating the production of Co⁺(N₂O)_n complexes generated following the ablation of a cobalt disc in the presence of an argon carrier gas seeded with 0.6% N₂O. Co⁺(N₂O)_n, CoO⁺(N₂O)_n and Co⁺(N₂O)_n–Ar complexes can be identified clearly. The size distribution of complexes generated can be controlled crudely by varying the partial pressure of N₂O and/or the backing pressure behind the pulsed valve. The equivalent mass spectra obtained for Rh⁺(N₂O)_n and Ir⁺(N₂O)_n and are shown in the ESI.† MO⁺(N₂O)_n oxide complexes are most prevalent in the cobalt mass spectrum and the Ir⁺ naked parent ion peak is almost undetectable suggesting highly efficient reaction and/or clustering in this case. Uniquely in the case of iridium ablation, M⁺(N₂O)_n(N₂) were also observed (see ESI†). These observations are entirely consistent with the M⁺ + N₂O reactivity reported by Böhme and coworkers⁸ and can be understood on the basis of the calculated reactive potential energy surfaces for the first reactive collision, M⁺ + N₂O, shown in Fig. 2.

Fig. 1 Time-of-flight mass spectrum of Co⁺(N₂O)_n complexes produced by ablation of a cobalt target in an argon carrier gas seeded with 0.6% N₂O. Asterisks (*) mark Co⁺O(N₂O)_n complexes and arrows indicate Ar-tagged complexes.

Fig. 2 Potential energy profiles for M⁺–N₂O insertion (M = (a) Co, (b) Rh, and (c) Ir). Black and red (blue in (a)) solid lines refer to ground and excited states of the metal cations, respectively. In each case, M⁺ + N₂O can form an N- or an O-bound complex, represented here as two pathways for each multiplicity (two lines from ground state cation and two lines from excited cation). Dashed lines represent the barrier to internal rotation, as the insertion reaction could begin from the N-bound complex, but also from the O-bound complex.

Given the singlet ground states of both N₂O and N₂, the O-atom transfer reaction

M⁺ + N₂O → MO⁺ + N₂, (1)

is only formally spin-allowed for M⁺ and MO⁺ states of the same multiplicity.⁸ Co⁺ has a (d⁸) ³F ground state⁵² whilst the ground state of CoO⁺ is ⁵Δ (though Armentrout and Beauchamp invoked a low-lying ³Σ⁻ state in their reactivity study).⁵³ Despite being exothermic, the Co⁺ + N₂O reaction is both spin-forbidden and experiences a significant barrier on the ground state surface. Unsurprisingly, then, this reaction is very slow.⁸ We find no evidence in any of our cobalt studies of the involvement of any excited electronic states. The ¹D surface shown in Fig. 2 is the lowest energy excited state with the same Co⁺ d⁸ configuration as the ground state (there are lower ⁵F and ³F excited states at 0.4 eV and 1.2 eV, respectively, but these have d⁷(⁴F)4s configurations). As will become clear, in all the M⁺(N₂O)_n systems studied here, low-spin states are stabilised by successive ligation.

The Rh⁺ + N₂O atom transfer reaction is the only one of the three systems here to be fully spin allowed, RhO⁺ having a ³Σ ground state. Despite being exothermic the reaction is very slow (k < 4 × 10⁻¹³ cm³ molecule⁻¹ s⁻¹)⁸ as a result of the large 0.7 eV barrier on the ground state surface. The d^{8 1}D state is the lowest excited state of different multiplicity and the only excited state predicted at 5500 K by Böhme and coworkers⁸ in their modelling of their inductively coupled plasma source. By contrast with the other two metal ions, the reaction of Ir⁺ with N₂O, despite being spin-forbidden on the quintet ground state, is fast. We determine a small (0.19 eV) barrier to reaction on the ground electronic state. Lavrov et al.⁸ account for the anomalous reaction rate as arising from spin mixing in the formation of the metal oxide cation – i.e., in the exit channel.

Each potential energy surface shown in Fig. 2 shows two entrance-channel complexes corresponding to nitrous oxide bonding to the metal centre via the terminal N-atom or the O-atom, respectively. In each case the N-bound isomer is the lower in energy. These structures form the basis for the understanding of the IRPD spectra to follow.

3.2 M⁺(N₂O)_n–Ar IRPD spectra

The infrared spectra of M⁺(N₂O)_n–Ar complexes (M = Co, Rh, Ir; n = 2–7) are presented in Fig. 3. Already from this overview it is clear that the evolution of the observed spectra with increased ligation, are markedly different for each of the three metal ions studied here. For this reason, the spectra for complexes of each metal ion are discussed separately.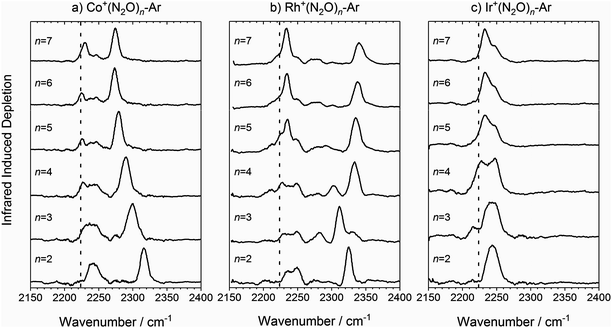

Fig. 3 Experimental IRPD spectra of M⁺(N₂O)_n–Ar (n = 2–7) complexes (M = (a) Co, (b) Rh and (c) Ir) in the region of the N₂O asymmetric (N=N) stretch. In each case, depletion of the ion signal occurs due to the loss of the Ar messenger atom. For comparison, the depletion intensity for each complex size was normalized with the maximum value in this region. The vertical dashed line indicates the wavenumber of the ν₃(N=N) mode in isolated N₂O at 2223.5 cm⁻¹.⁵¹

3.2.1 Co⁺(N₂O)_n–Ar IRPD spectra. Fig. 3a shows the IRPD spectra for the Co⁺(N₂O)_n–Ar (n = 2–7) complexes. In each spectrum two distinct spectral features can be identified; one close to the N=N stretching frequency in free N₂O at 2223.5 cm⁻¹,⁵¹ and a second significantly blue-shifted from the first by between 93 and 50 cm⁻¹. The spectral feature near 2240 cm⁻¹ is broad suggesting it is a blended feature of multiple vibrational bands and its integrated intensity drops with increasing complex size. A distinct feature at the free N₂O stretching frequency is apparent in the spectra for all complexes n > 2 size, suggesting the presence of weakly-interacting ligands.

The second spectral feature undergoes a smooth red-shift (or decreasing blue-shift relative to the first band) with increasing ligand number from 2316 cm⁻¹ for n = 2 to 2274 cm⁻¹ for n = 7. In these regards, the trends in the spectra of the Co⁺(N₂O)_n–Ar complexes show close similarity with those reported previously for the coinage metal N₂O complexes²⁴ and a similar rationale can be applied to their understanding.

Fig. 4 shows a representation of the calculated Co⁺N₂O potential energy surface in the entrance channel. The line shows the calculated minimum energy as a function of Co⁺–N–N bond angle with 0° marking the linear Co⁺–NNO structure (i.e., η¹via the N atom) which represents the lowest energy entrance-channel structure. A second, higher-lying, double-well minimum corresponding to the bent Co⁺ONN structure (η¹via the O atom) is observed at 155°/205°. The N- and O-bound minima are separated by a large barrier to N₂O internal rotation of >1 eV. Rapid cooling within our free-jet expansion permits the formation of excited isomeric forms trapped behind such barriers, leading to the possibility of isomers with both N-bound and O-bound ligands. This ability of N₂O to bind in two distinct orientations with differing binding energies leads to complicated growth kinetics. For example, the binding of a ligand in an N-bound orientation can potentially displace an existing O-bound ligand but the reverse is less likely (indeed impossible without significant internal energy). For this reason, larger complexes will probably be richer in N-bound ligands.

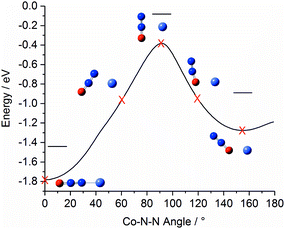Fig. 4 Minimum-energy pathway of triplet Co⁺N₂O as a function of Co–N–N bond angle, illustrating the relative energies of the N- and O-bound minima. For this pathway the N₂O geometry was allowed to relax. Horizontal lines indicate the energy of the respective geometry-optimised structures including zero point correction. The equivalent pathways of the Rh⁺N₂O and Ir⁺N₂O complexes are qualitatively similar (see ESI†).

It will be convenient in what follows to adopt a succinct notation ^2S+1M⁺N^xO^y for a particular structure in which x and y are integer values indicating the number of N- and O-bound ligands, respectively. Clearly x + y = n. So, for example, ¹M⁺N²O¹ represents a singlet state of a M⁺(N₂O)₃ isomer with two N-bound ligands and one O-bound ligand.

The Co⁺(N₂O)_n–Ar spectra can be understood qualitatively from DFT simulations of the Co⁺(N₂O)₂–Ar complex which shows the N- and O-bound ligands to be spectroscopically distinct isomers. Fig. 5 shows the experimental IRPD spectrum of Co⁺(N₂O)₂–Ar together with spectral simulations of the ³Co⁺N², ³Co⁺N¹O¹ and ³Co⁺O² isomers. Table S1 in the ESI† gives the relative energies of all calculated structures together with those of other electronic states. As discussed above, given the relative energies of excited spin states only the triplet states are likely to contribute significantly to the spectra obtained.

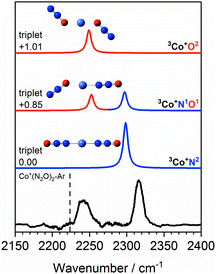Fig. 5 Experimental IRPD spectrum of the Co⁺(N₂O)₂–Ar complex along with simulated IR spectra of low-lying isomers of the ground triplet state in the region of the N₂O asymmetric (N=N) stretch. Simulated IR bands corresponding to N-bound and O-bound ligands are indicated in blue and red, respectively. The relative energies of different isomers are given in eV. The vertical dashed line indicates the wavenumber of the ν₃(N=N) mode in isolated N₂O at 2223.5 cm⁻¹.⁵¹

The ³Co⁺N² isomer is the lowest energy molecularly-bound structure. It is clear from Fig. 5, however, that the ³Co⁺N² structure alone cannot account for the two spectral bands observed experimentally and that O-bound ligands (in the form of ³Co⁺N¹O¹ and ³Co⁺O² isomers) must be present. The two bands observed experimentally can be assigned as follows: the lower wavenumber band at 2240 cm⁻¹ is attributed to the N=N stretch in O-bound ligands. Such binding represents minimal perturbation to the N=N bond, leading to a fundamental band close to that in free N₂O. The higher wavenumber feature (2316 cm⁻¹) arises from N-bound ligands. The binding mechanism for N-bound ligands is dominated by electron donation from the N₂O HOMO−1, 7σ orbital to the metal centre. As the 7σ orbital is antibonding with respect to the N=N bond, this results in a slightly stronger N=N bond reflected in a spectral blue-shift.^13,14,24

The two bands in the observed spectrum clearly indicate the presence of both O- and N-bound ligands. Given the relative energies of the different isomers, it is inconceivable that we generate a pure population of the ³Co⁺N¹O¹ structure and we conclude that a mixture of isomers is present in our molecular beam.

The first two N₂O ligands bind to the Co⁺ centre tightly with M⁺–L bond dissociation energies of 1.62 eV. Subsequent ligands are bound less strongly but can still influence the IRPD spectra. The lower wavenumber feature in the spectrum becomes broader with increasing ligation as not only O-bound ligands contribute in this region, but also less strongly interacting N-bound ligands. As a result, the interpretation of the spectra in this region becomes less clear cut.

As n increases further, the efficiency of σ-donation by N-bound core ligands drops leading to a smooth red-shift in the higher frequency vibrational band (see Fig. 3a). This red-shift appears to cease at n = 6, suggesting the completion of a coordination shell which is confirmed by DFT calculations and is consistent with the expected octahedral symmetry of a high-spin d⁸ complex.

3.2.2 Rh⁺(N₂O)_n–Ar spectra. The IRPD spectra for the Rh⁺(N₂O)_n–Ar (n = 2–7) complexes are shown in Fig. 3b. Again, two distinct spectral features are observed which we can assign to N- and O-bound core and outer-ligands. It is clear, however, both from the presence of new spectral features and a contrasting trend in the band positions with n that the Rh⁺(N₂O)_n complexes are more complicated than their Co⁺(N₂O)_n counterparts.

Fig. 6 shows the IRPD spectrum of Rh⁺(N₂O)₂–Ar along with the simulated spectra for energetically low-lying isomers of singlet and triplet states. As for Co⁺(N₂O)₂, the observed 2325 cm⁻¹ and 2240 cm⁻¹ bands can clearly be attributed to N- and O-bound ligands, respectively, i.e., a separation of ca. 85 cm⁻¹. Although the observed spectral splitting of the two bands is slightly better reproduced in the singlet state structures (Δ[small upsilon, Greek, tilde] (¹Rh⁺N¹O¹) = 96 cm⁻¹c.f. Δ[small upsilon, Greek, tilde] (³Rh⁺N¹O¹) = 66 cm⁻¹), for n = 2 the singlet structures are calculated to lie markedly higher in energy than the triplet states and we have no reason to believe that they contribute significantly.

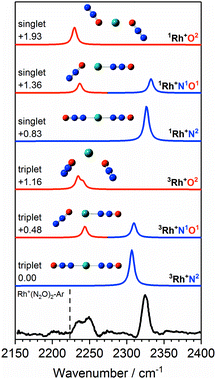Fig. 6 Experimental IRPD spectrum of the Rh⁺(N₂O)₂–Ar complex along with simulated IR spectra of low-lying singlet and triplet isomers in the region of the N₂O asymmetric (N=N) stretch. Simulated IR bands corresponding to N-bound and O-bound ligands are indicated in blue and red, respectively. Relative energies are given in eV. The vertical dashed line indicates the wavenumber of the ν₃(N=N) mode in isolated N₂O at 2223.5 cm⁻¹.⁵¹

The IRPD spectra begin to get more complex with the Rh⁺(N₂O)₃–Ar species – see Fig. 7 which shows simulated spectra for a range of ^1/3Rh⁺N^xO^y isomers – as new bands appear. The signature of the core N- and O-bound ligands is clear in the intense feature at 2312 cm⁻¹ and the broad feature 2225–2250 cm⁻¹. A new band around 2280 cm⁻¹ reflects the third ligand N-binding less strongly than the two core ligands. It has an increased M⁺–NNO bond length of 2.23 Å compared with 2.07 Å for the core ligands and is clearly reproduced in the simulated spectra of the ³Rh⁺N³, ³Rh⁺N²O¹ and ³Rh⁺N¹O² isomers.

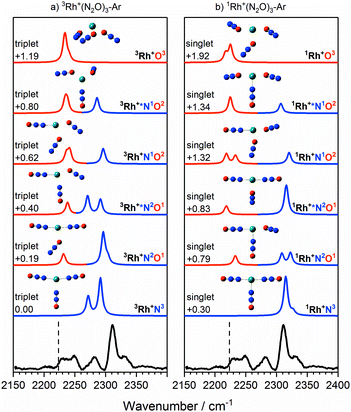Fig. 7 Experimental IRPD spectrum of the Rh⁺(N₂O)₃–Ar complex along with simulated IR spectra of low-lying (a) triplet-state isomers and (b) singlet-state isomers in the region of the N₂O asymmetric (N=N) stretch. Simulated IR bands corresponding to N-bound and O-bound ligands are indicated in blue and red, respectively. The relative energies of different isomers are given in eV. The vertical dashed line indicates the wavenumber of the ν₃(N=N) mode in isolated N₂O at 2223.5 cm⁻¹.⁵¹

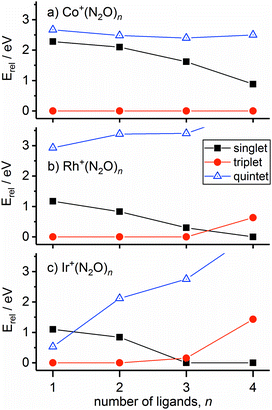
In the case of the rhodium complexes an additional complication rises due to low-lying electronically excited states. For the bare ion the d^{8 1}D state lies ca. 1.4 eV higher than the ³F ground state.^54,55 However, upon complexation the singlet state is strongly stabilised such that by n = 3 the ¹Rh⁺N³ isomer is calculated to lie only 0.3 eV higher than the ³Rh⁺N³ ground state. Fig. 8 shows the relative energies of the lowest isomeric forms of singlet, triplet and quintet states of M⁺(N₂O)_n as a function of ligand number. Tables S1–S3 in the ESI† present the calculated relative energies of all M⁺(N₂O)_n structural isomers identified in this study.

Fig. 8 Calculated lowest energy isomers of singlet (black squares), triplet (red circles) and quintet (blue open triangles) states of (a) Co⁺(N₂O)_n, (b) Rh⁺(N₂O)_n, and (c) Ir⁺(N₂O)_n, as a function of ligand number. Energies are relative to the global minimum structure for each n.

We believe the shoulder at 2330 cm⁻¹ in Fig. 7 indicates the emergence of the singlet state in our spectrum. As shown in Fig. 8, the singlet state becomes comparable in energy with the triplet around n = 3 and becomes the ground state at larger n. It seems likely that the observed spectrum of Rh⁺(N₂O)₃–Ar results from a complex combination of multiple isomers of two different electronic states.

The singlet and triplet states still have comparable energy in the n = 4 complexes although now the singlet state is the lower in energy, and this is reflected in an intensity alternation in the spectrum (see Fig. 3b). Fig. 9 shows the IRPD spectrum of the Rh⁺(N₂O)₄–Ar complex, alongside simulated IR spectra from various calculated singlet and triplet isomers. Reflecting the low-spin d⁸ configuration, a square-planar ¹Rh⁺N⁴ isomer is the calculated global minimum, with the ³Rh⁺N⁴ counterpart 0.63 eV higher in energy.

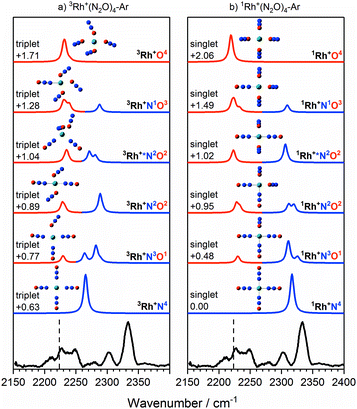Fig. 9 Experimental IRPD spectrum of the Rh⁺(N₂O)₄–Ar complex along with simulated IR spectra of low-lying (a) triplet-state isomers and (b) singlet-state isomers in the region of the N₂O asymmetric (N=N) stretch. Simulated IR bands corresponding to N-bound and O-bound ligands are indicated in blue and red, respectively. Relative energies are in eV. The vertical dashed line indicates the wavenumber of the ν₃(N=N) mode in isolated N₂O at 2223.5 cm⁻¹.⁵¹

It is not uncommon for the spin state of the global minimum to change upon increasing ligation.^56,57 For example, in the case of V⁺(CO)_n complexes,^56,57 a lower (triplet) multiplicity state appears for n ≥ 4. For Rh⁺(N₂O)_n, the switch to the lower multiplicity, singlet state at n = 4 is consistent with the adoption of square-planar geometries which are known to be favoured by low-spin d⁸ complexes. In such cases n = 4 represents a complete shell.⁵⁸

As in the n = 3 case, a combination of multiple isomers of both spin states provides a satisfactory understanding of the spectrum (see Fig. 9). The band at 2333 cm⁻¹ can be assigned to the now familiar N-bound ligand in a singlet isomer. This band lies markedly to the blue of the strongest feature in the n = 3 spectra (Fig. 7), reflecting the change in structure/spin state. The weaker 2302 cm⁻¹ band is most likely a strongly N-bound ligand in a triplet isomer (e.g., ³Rh⁺N²O² or ³Rh⁺N³O¹) but could be a weakly-interacting N-bound ligand in a singlet state isomer.

Once the singlet state is unambiguously the lowest energy state for n > 4, the spectra of the Rh⁺(N₂O)_n–Ar complexes become simpler again. By contrast with Co⁺(N₂O)_n and the coinage metal complexes²⁴ the blue-shift in the N-bound band increases further with n reflecting ever stronger σ-donation as captured in the calculated structures. n = 4 represents a complete coordination shell for the square-planar Rh⁺(N₂O)_n complexes. As further N₂O ligands add, the four metal–ligand (M⁺–N) bond distances in the “core” shorten, increasing the σ-electron density donation leading to an increased spectral blue-shift in the band as observed in the experimental spectra (Fig. 10).

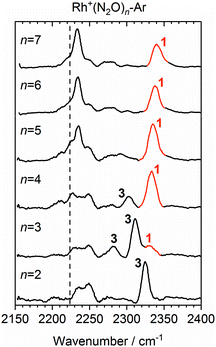Fig. 10 Experimental IRPD spectra of Rh⁺(N₂O)_n–Ar (n = 2–7) complexes in the region of the N₂O asymmetric (N=N) stretch. For comparison, the depletion intensity for each complex size was normalized with the maximum value in this region. N-Bound bands are assigned to a singlet isomer (1) or a triplet isomer (3). The vertical dashed line indicates the wavenumber of the ν₃(N=N) mode in isolated N₂O at 2223.5 cm⁻¹.⁵¹

In the light of the above interpretations, it is possible to assign bands in the various spectra as arising from singlet and triplet isomers, accordingly as shown in Fig. 10. Once the spin configuration changes from triplet to singlet at n = 4, the singlet remains the lowest energy multiplicity predicted for the higher order complexes, n = 5–7 and dominate the spectra.

Finally, we cannot rule out the existence of inserted ORh⁺N₂(N₂O)_n−1 structures in these spectra. In most cases these structures represents the true global minimum structure, albeit behind a significant barrier to reaction (see Fig. 2). The N₂ stretch, which is weakly IR-allowed in complexation to an ion, is predicted to lie in the same region. However, in most cases the overall O-atom transfer reaction (1) is strongly exothermic and it seems unlikely that an N₂ moiety could remain bound once significant energy is released upon formation of the MO⁺ bond.

3.2.3 Ir⁺(N₂O)_n–Ar spectra. The IRPD spectra for the Ir⁺(N₂O)_n–Ar (n = 2–7) complexes are shown in Fig. 3c and are quite unlike those of any other M⁺(N₂O)_n system we have studied. Only a single, partially resolved feature is observed, slightly blue-shifted from the free N₂O vibration previously interpreted as arising from O-bound ligands (ca. 2260–2220 cm⁻¹).

The ground state of Ir⁺ is a 5d⁷(⁴F)6s ⁵F state with a 5d^{8 3}F state ca. 0.25 eV higher.⁵⁹ Complexation with even a single N₂O stabilises the ³F state of the ion relative to the ⁵F ground state and the ³Ir⁺N² isomer is clearly the lowest energy entrance-channel structure (see Fig. 8).

Fig. 11 shows a comparison of the Ir⁺(N₂O)₂ spectrum with calculated spectra of low-lying isomers. The simulated spectra for the ³Ir⁺N² and ³Ir⁺N¹O¹ isomers agree very poorly with the observed spectrum in which there is no evidence of an “N-bound feature” around 2300 cm⁻¹. Given that the ³Ir⁺O² isomer lies >1 eV above the ground state it is inconceivable that a pure distribution of this species is formed.

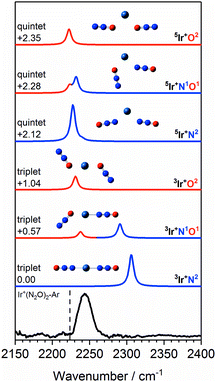Fig. 11 Experimental IRPD spectrum of the Ir⁺(N₂O)₂–Ar complex along with simulated IR spectra of low-lying triplet and quintet isomers in the region of the N₂O asymmetric (N=N) stretch. Simulated IR bands corresponding to N-bound and O-bound ligands are indicated in blue and red, respectively. Relative energies are given in eV. The vertical dashed line indicates the wavenumber of the ν₃(N=N) mode in isolated N₂O at 2223.5 cm⁻¹.⁵¹

Despite lying considerably higher in energy, the simulated spectra of the quintet states agree well with the experimental spectrum as no significant blue-shift is predicted even in the N-bound ligands. In the quintet, higher population of strongly antibonding orbitals (including a 6s–7σ interaction) weakens the N-bound interaction and is reflected in non-linear structures (see Fig. 11). As a result, the predicted bands in all ligands appear in the region 2220–2240 cm⁻¹. The observed spectral band is notably broader than in the Co⁺(N₂O)₂–Ar and Rh⁺(N₂O)₂–Ar spectra and we thus assign this feature to a convolution of the three quintet isomers, ⁵Ir⁺N², ⁵Ir⁺N¹O¹ and ⁵Ir⁺O².

One possible explanation for the absence of triplet states comes from the calculated M⁺ + N₂O reaction pathways shown in Fig. 2. On the triplet state surface the barrier to the O-atom transfer reaction is submerged and hence any reaction on the triplet surface can be assumed to proceed to completion resulting in the sequential production of IrO_m⁺. This is consistent with the single collision reaction results of Böhme and coworkers⁸ as well as the apparent complete loss of the parent Ir⁺ signal in our time of flight spectra (Fig. S51, ESI†).

In contrast, on the quintet surface, a small (0.19 eV) but real barrier to reaction exists (see Fig. 2c) and, under the rapid quenching conditions of our expansion, reactants might easily become trapped in the weakly-bound entrance channel structures. If such complexes then form seeds for subsequent clustering without inducing a change in spin state, then the only complexes observed would be quintet states with spectra as shown in Fig. 11 which agree well with the observed IRPD spectra. Such an interpretation would imply highly inefficient surface-crossings between quintet and triplet surfaces for all complexes studied here.

4. Discussion

One of the most striking findings of this study is the difference observed in the spectra of the three transition metal ions studied. In contrast, only subtle differences were observed in the structures and spectra of N₂O complexes with Cu⁺, Ag⁺ and Au⁺.²⁴ The differences here appear to correlate with the importance of low-lying excited electronic states and, in particular, the differing effects successive ligation has on the ground and excited states of the metal ions (see Fig. 8).

In the simplest case of Co⁺, rather like in the coinage metal ions, a satisfactory understanding of the observed Co⁺(N₂O)_n spectra in terms of N- and O-bound ligands, is achieved by considering only the ground electronic state. The excited states all lie markedly higher in energy, at least up to n = 4. A smooth red-shift in the spectral band denoting N-bound ligands is observed with successive ligation as new ligands impair the efficiency of σ-donation by the two core ligands.

The spectra of Rh⁺(N₂O)_n and Ir⁺(N₂O)_n complexes, and their variation with n, are qualitatively different to the other systems. Particularly in the case of Rh⁺(N₂O)_n, the IR spectra contain evidence for the role of excited electronic states with new bands appearing in the spectra around n = 3, 4 just as the singlet state is calculated to become the ground state. Such effects should not be surprising – it is exactly this abundance of low-lying electronic states which makes the platinum group metals so useful in catalysis.

It is worth emphasising that for all the metal–ligand cases studied here, a satisfactory understanding of the spectra observed is achieved by considering the calculated low-lying spin states and structures predicted by density functional theory. This contrasts with the naked metal clusters (M_n^+/0/−) of the same elements, the electronic and geometrical structures of which remain, in some cases, a matter of heated discussion.^60–64

5. Conclusions

The structures of gas-phase M⁺(N₂O)_n complexes (M = Co, Rh, Ir; n = 2–7) have been studied using a combination of IRPD spectroscopy and density functional theory. The spectra of the complexes for the three transition metal ions are markedly different from one another and evolve in contrasting ways with increasing ligand number, n.

Spectral simulations based on calculated energetically low-lying structures provide clear explanations for the spectra observed in terms of isomers with spectroscopically distinguishable N- and O-bound ligands. In all cases, the N-bound structures represent the lower in energy but significant barriers to free internal rotation allow for the trapping of O-bound ligands. The IRPD spectra of the Rh⁺(N₂O)_n and Ir⁺(N₂O)_n complexes show additional evidence underlying the importance of low-lying excited electronic states including, in the case of the former, a switch in the spin multiplicity of the ground state at or around n = 4.

The combination of multiple binding motifs and low-lying electronic states gives rise to an unusually rich and diverse range of structures for these complexes. The fact that N- and O-bound core ligands are spectroscopically distinguishable gives rise to the tantalising possibility of addressing individual ligands with known binding motifs. In turn this offers the possibility of controllable infrared excitation for the study of intra-complex chemistry.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This paper is submitted to the themed issue on Photodissociation and Reaction Dynamics timed to coincide with Prof Mike Ashfold's 65th birthday. Mike has been a hugely supportive and inspirational figure in the UK gas-phase chemical physics community and the current health of the discipline owes much to his leadership. This work is funded by EPSRC under Programme Grant EP/L005913. EMC is also grateful to the EPSRC for his graduate studentship. The authors are grateful to Prof John McGrady for helpful discussions. The authors acknowledge the use of the University of Oxford Advanced Research Computing (ARC) facility in carrying out this work. http://dx.doi.org/10.5281/zenodo.22558.

References

1. M. J. Prather, Science, 1998, 279, 1339–1341.
2. A. R. Ravishankara, J. S. Daniel and R. W. Portmann, Science, 2009, 326, 123–125.
3. D. K. Böhme and H. Schwarz, Angew. Chem., Int. Ed., 2005, 44, 2336–2354.
4. WMO, Scientific Assessment of Ozone Depletion: 2014, World Meteorological Organization, Global Ozone Research and Monitoring Project-Report, No. 55, Geneva, Switzerland, 2014, p. 416.
5. W. B. Tolman, Angew. Chem., Int. Ed., 2010, 49, 1018–1024.
6. P. Chen, S. I. Gorelsky, S. Ghosh and E. I. Solomon, Angew. Chem., Int. Ed., 2004, 43, 4132–4140.
7. V. Rosca, M. Duca, M. T. de Groot and M. T. M. Koper, Chem. Rev., 2009, 109, 2209–2244.
8. V. V. Lavrov, V. Blagojevic, G. K. Koyanagi, G. Orlova and D. K. Böhme, J. Phys. Chem. A, 2004, 108, 5610–5624.
9. F. Kapteijn, J. Rodriguez-Mirasol and J. A. Moulijn, Appl. Catal., B, 1996, 9, 25–64.
10. A. Delabie, C. Vinckier, M. Flock and K. Pierloot, J. Phys. Chem. A, 2001, 105, 5479–5485.
11. A. Stirling, J. Am. Chem. Soc., 2002, 124, 4058–4067.
12. E. S. Kryachko, O. Tishchenko and M. T. Nguyen, Int. J. Quantum Chem., 2002, 89, 329–340.
13. X. Jin, G. Wang and M. Zhou, J. Phys. Chem. A, 2006, 110, 8017–8022.
14. G. Wang, X. Jin, M. Chen and M. Zhou, Chem. Phys. Lett., 2006, 420, 130–134.
15. G. Dietrich, K. Lutzenkirchen, S. Becker, H. U. Hasse, H. J. Kluge, M. Lindinger, L. Schweikhard, J. Ziegler and S. Kuznetsov, Ber. Bunsen-Ges. Phys. Chem. Chem. Phys., 1994, 98, 1608–1612.
16. P. A. Hintz and K. M. Ervin, J. Chem. Phys., 1995, 103, 7897–7906.
17. O. P. Balaj, I. Balteanu, T. T. J. Rossteuscher, M. K. Beyer and V. E. Bondybey, Angew. Chem., Int. Ed., 2004, 43, 6519–6522.
18. I. Balteanu, O. P. Balaj, M. K. Beyer and V. E. Bondybey, Phys. Chem. Chem. Phys., 2004, 6, 2910–2913.
19. D. Harding, M. S. Ford, T. R. Walsh and S. R. Mackenzie, Phys. Chem. Chem. Phys., 2007, 9, 2130–2136.
20. M. L. Anderson, A. Lacz, T. Drewello, P. J. Derrick, D. P. Woodruff and S. R. Mackenzie, J. Chem. Phys., 2009, 130, 064305.
21. I. S. Parry, A. Kartouzian, S. M. Hamilton, O. P. Balaj, M. K. Beyer and S. R. Mackenzie, J. Phys. Chem. A, 2013, 117, 8855–8863.
22. M. K. Beyer, C. B. Berg and V. E. Bondybey, Phys. Chem. Chem. Phys., 2001, 3, 1840–1847.
23. M. T. Rodgers, B. Walker and P. B. Armentrout, Int. J. Mass Spectrom., 1999, 182, 99–120.
24. E. M. Cunningham, A. S. Gentleman, P. W. Beardsmore, A. Iskra and S. R. Mackenzie, J. Phys. Chem. A, 2017, 121, 7565–7571.
25. M. S. Ford, M. L. Anderson, M. P. Barrow, D. P. Woodruff, T. Drewello, P. J. Derrick and S. R. Mackenzie, Phys. Chem. Chem. Phys., 2005, 7, 975–980.
26. M. L. Anderson, M. S. Ford, P. J. Derrick, T. Drewello, D. P. Woodruff and S. R. Mackenzie, J. Phys. Chem. A, 2006, 110, 10992–11000.
27. D. Harding, S. R. Mackenzie and T. R. Walsh, J. Phys. Chem. B, 2006, 110, 18272–18277.
28. A. Yamada, K. Miyajima and F. Mafuné, Phys. Chem. Chem. Phys., 2012, 14, 4188–4195.
29. H. Xie, M. Ren, Q. Lei and W. Fang, J. Phys. Chem. A, 2011, 115, 14203–14208.
30. D. J. Harding, R. D. L. Davies, S. R. Mackenzie and T. R. Walsh, J. Chem. Phys., 2008, 129, 124304.
31. S. M. Hamilton, W. S. Hopkins, D. J. Harding, T. R. Walsh, P. Gruene, M. Haertelt, A. Fielicke, G. Meijer and S. R. Mackenzie, J. Am. Chem. Soc., 2010, 132, 1448–1449.
32. S. M. Hamilton, W. S. Hopkins, D. J. Harding, T. R. Walsh, M. Haertelt, C. Kerpal, P. Gruene, G. Meijer, A. Fielicke and S. R. Mackenzie, J. Phys. Chem. A, 2011, 115, 2489–2497.
33. A. C. Hermes, S. M. Hamilton, W. S. Hopkins, D. J. Harding, C. Kerpal, G. Meijer, A. Fielicke and S. R. Mackenzie, J. Phys. Chem. Lett., 2011, 2, 3053–3057.
34. M. A. Duncan, Annu. Rev. Phys. Chem., 1997, 48, 69–93.
35. L. G. Dodson, M. C. Thompson and J. M. Weber, Annu. Rev. Phys. Chem., 2018, 69, 231–252.
36. J. M. Lisy, Int. Rev. Phys. Chem., 1997, 16, 267–289.
37. L. Wang, G. Wang, H. Qu, Z. H. Li and M. Zhou, Phys. Chem. Chem. Phys., 2014, 16, 10788–10798.
38. Y. Li, L. Wang, H. Qu, G. Wang and M. Zhou, J. Phys. Chem. A, 2015, 119, 3577–3586.
39. A. Iskra, A. S. Gentleman, A. Kartouzian, M. J. Kent, A. P. Sharp and S. R. Mackenzie, J. Phys. Chem. A, 2017, 121, 133–140.
40. B. A. Mamyrin, V. I. Karataev, D. V. Shmikk and V. A. Zagulin, J. Exp. Theor. Phys., 1973, 37, 45.
41. O. Rodriguez and J. M. Lisy, J. Phys. Chem. A, 2011, 115, 1228–1233.
42. O. Rodriguez Jr and J. M. Lisy, Chem. Phys. Lett., 2011, 502, 145–149.
43. P. Ayotte, G. H. Weddle, J. Kim and M. A. Johnson, J. Am. Chem. Soc., 1998, 120, 12361–12362.
44. M. Okumura, L. I. Yeh, J. D. Myers and Y. T. Lee, J. Phys. Chem., 1990, 94, 3416–3427.
45. M. Okumura, L. I. Yeh, J. D. Myers and Y. T. Lee, J. Chem. Phys., 1986, 85, 2328–2329.
46. M. B. Knickelbein and W. J. C. Menezes, J. Phys. Chem., 1992, 96, 6611–6616.
47. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
48. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
49. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
50. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
51. G. Herzberg, Molecular Spectra and Molecular Structure: II Infrared and Raman Spectra of Polyatomic Molecules, Krieger, Malabar, Florida, 1991.
52. J. C. Pickering, A. J. J. Raassen, P. H. M. Uylings and S. Johansson, ApJS, 1998, 117, 261.
53. P. B. Armentrout, L. F. Halle and J. L. Beauchamp, J. Chem. Phys., 1982, 76, 2449–2457.
54. F. J. Sancho, An. R. Soc. Esp. Fis. Quim., Ser. A, 1958, 54, 41–64.
55. Y. Shadmi, Bull. Res. Counc. Isr., Sect. F, 1961, 9(4), 141–170.
56. M. R. Sievers and P. B. Armentrout, J. Phys. Chem., 1995, 99, 8135–8141.
57. A. M. Ricks, A. D. Brathwaite and M. A. Duncan, J. Phys. Chem. A, 2013, 117, 1001–1010.
58. L. E. Orgel, An Introduction to Transition-Metal Chemistry: Ligand-Field Theory, Methuen, Wiley, 1963.
59. T. A. M. van Kleef and B. C. Metsch, Physica B+C, 1978, 95, 251–265.
60. D. J. Harding, T. R. Walsh, S. M. Hamilton, W. S. Hopkins, S. R. Mackenzie, P. Gruene, M. Haertelt, G. Meijer and A. Fielicke, J. Chem. Phys., 2010, 132, 011101.
61. D. J. Harding, P. Gruene, M. Haertelt, G. Meijer, A. Fielicke, S. M. Hamilton, W. S. Hopkins, S. R. Mackenzie, S. P. Neville and T. R. Walsh, J. Chem. Phys., 2010, 133, 214304.
62. A. S. Chaves, M. J. Piotrowski and J. L. F. Da Silva, Phys. Chem. Chem. Phys., 2017, 19, 15484–15502.
63. J. L. F. Da Silva, M. J. Piotrowski and F. Aguilera-Granja, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 125430.
64. D. C. Navarro-Ibarra, J. F. Aguilera-Granja and R. A. Guirado-Lopez, Eur. Phys. J. D, 2018, 72, 129.

---

Footnote

† Electronic supplementary information (ESI) available: Calculated low energy structures and energies, additional time of flight spectra, additional IRPD spectra and potential energy surfaces. See DOI: 10.1039/c8cp05995k

---