Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hydrogen adsorption on transition metal carbides: a DFT study†
Fabrizio
Silveri
 *,
Matthew G.
Quesne
*,
Matthew G.
Quesne
 ,
Alberto
Roldan
,
Alberto
Roldan
 ,
Nora H.
de Leeuw
,
Nora H.
de Leeuw
 and
C. Richard A.
Catlow
and
C. Richard A.
Catlow
School of Chemistry, Cardiff University, Main Building, Park Place, Cardiff CF10 3AT, UK. E-mail: SilveriF@Cardiff.ac.uk; CatlowR@Cardiff.ac.uk
First published on 17th January 2019
Abstract
Transition metal carbides are a class of materials widely known for both their interesting physical properties and catalytic activity. In this work, we have used plane-wave DFT methods to study the interaction with increasing amounts of molecular hydrogen on the low-index surfaces of four major carbides – TiC, VC, ZrC and NbC. Adsorption is found to be generally exothermic and occurs predominantly on the surface carbon atoms. We identify trends over the carbides and their surfaces for the energetics of the adsorption as a function of their electronic and geometrical characteristics. An ab initio thermodynamics formalism is used to study the properties of the slabs as the hydrogen coverage is increased.
Introduction
One of the key scientific and technical challenges of the 21st century is the need to meet the global demand for energy in a clean, secure and sustainable way,1,2 by overcoming remaining issues of electricity storing and pollution.3 The hydrogen evolution reaction (HER) has been intensively studied as a route to produce H2 from H2O, with the primary goal of using molecular hydrogen in carbon-free fuel cells and as a reductant to recycle CO2. The HER is most effectively catalysed by Pt electrodes, which allow the reaction to be driven using a low overpotential.4,5 However, the high cost and low supply of Pt make it an impractical catalyst for global scale production of H2.Low cost materials have been investigated in recent years with the aim of obtaining similar performances to Pt.6,7 One such avenue of research is the class of materials known as transition metal carbides (TMCs), which couple low cost and high durability with interesting catalytic properties for many reactions,8–11 as originally highlighted by the seminal work by Levy and Boudart in 1973.12
Transition metals can form carbides in a variety of structures and stoichiometries, depending on their position in the periodic table and the extent of defects in the structure.13,14 Monocarbides and non-stoichiometric carbides of early transition metals are found to have stable rock-salt bulk structures,15–20 while metals at the centre of the transition series have more complex stoichiometries and structures.11,21,22 These compounds combine some of the physical properties of transition metals, ionic and covalent solids,23,24 which can be further modified by tuning the amount of carbon in the lattice and the bonding character of the metal–carbon bond.25,26
The catalytic behaviour of TMCs has been investigated for a wide range of reactions, such as hydrogenation, CO2 reduction, water-gas shift, hydro-treatment and a number of processes involving hydrocarbons, including isomerization and methane reforming.27–33 For the hydrogen evolution reaction, these materials have been used with promising results as both supports for platinum electrocatalysts33 and as catalysts themselves, either as bulk materials or nanoparticles.11,21,34 However, TMC catalysts have still not seen widespread adoption in industrial processes.35
In this work, the interaction between molecular hydrogen and four TMCs from groups IV and V is studied using plane-wave Density Functional Theory (DFT) methods. TiC, ZrC, VC and NbC, all with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry and the rock-salt structure, are modelled and cut into four different low index surfaces, i.e. the (001) and (011) surfaces and the carbon- and metal-terminations of the (111) plane. We have identified trends in the energetic and electronic effects of the H2 adsorption from which we can make predictions concerning the H2 evolution under specific conditions on the different surfaces. The metal carbides were chosen after a comprehensive review of bulk and surface properties showed that they had promising properties as potential catalysts for CO2 hydrogenation reactions. Previous experimental and computational results27,36 suggest that TiC and its immediate neighbours are good candidates for H2 evolution and CO2 reduction and could be superior to other transition metal carbides with 1
1 stoichiometry and the rock-salt structure, are modelled and cut into four different low index surfaces, i.e. the (001) and (011) surfaces and the carbon- and metal-terminations of the (111) plane. We have identified trends in the energetic and electronic effects of the H2 adsorption from which we can make predictions concerning the H2 evolution under specific conditions on the different surfaces. The metal carbides were chosen after a comprehensive review of bulk and surface properties showed that they had promising properties as potential catalysts for CO2 hydrogenation reactions. Previous experimental and computational results27,36 suggest that TiC and its immediate neighbours are good candidates for H2 evolution and CO2 reduction and could be superior to other transition metal carbides with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometries. Whilst these prior studies have clearly provided important insight, our work offers the first comprehensive theoretical study into hydrogen adsorption on all low-index surfaces of TiC, ZrC, VC and NbC.
1 stoichiometries. Whilst these prior studies have clearly provided important insight, our work offers the first comprehensive theoretical study into hydrogen adsorption on all low-index surfaces of TiC, ZrC, VC and NbC.
Computational details
All calculations have been performed within the framework of the density functional theory (DFT) as implemented in the VASP (Vienna Ab initio Software Package) code.37–39 The electronic energy was obtained using PAW (projected augmented wave) potentials40 and plane-wave basis sets, respectively, for core and valence electrons, using the Perdew–Burke–Ernzerhof (PBE) functional.41 Corrections were added to account for long-range interactions by the semi-empirical Grimme D3 dispersion method42 and for non-spherical contributions to the PAW potentials as incorporated in the code. All energies were converged within a cutoff of 520 eV and an electronic self-consistent field (SCF) threshold of 10−5 eV. Convergence was determined using the tetrahedron method, implementing Blochl corrected smearing43 and in all cases spin polarization was enabled, with the only exception of the isolated H2 closed shell molecule.The surfaces of the TMCs in the study were simulated by 2 × 2 × 3 supercell slab models generated via the METADISE code, cutting the bulk along the (001), (011) and (111) planes. Each slab has 6 atomic layers and 16 atoms per layer. The (001) and (011) surfaces are created such that they preserve the bulk stoichiometry, resulting in an equal number of carbon and metal atoms being exposed to the vacuum. Conversely, the (111) plane is parallel to carbon and metal layers, resulting in two possible surface terminations that respectively expose carbon and metal atoms in the surface. Such a protocol has been applied previously to TMCs and has been shown to describe accurately the electronic and structural properties of the (111) surfaces, as will be further discussed below.30,36 To avoid interaction along the axis perpendicular to the surface, 12 Å of vacuum were added in that direction. The 5 × 5 × 1 K-points reciprocal lattice matrix was generated using the Monkhorst–Pack method. The energy of the system was minimized by keeping the cell parameters fixed at their bulk-optimised value and allowing relaxation of all atoms, apart from those belonging to the 2 bottom layers of the TMC, which were kept fixed. The minimum energy structures were found using a built-in DIIS algorithm with a convergence force threshold of 10−2 eV Å−1.
The interactions between the different surfaces and hydrogen were compared using the adsorption energy (ΔEads) as calculated by:
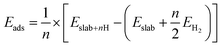 | (1) |
Atomic charges were calculated on specific configurations through a Bader charge analysis,44 as implemented by Henkelman and co-workers.45,46 The reported work functions (Φ) were calculated by subtracting the Fermi energy from the vacuum energy, extracted from the local potential by averaging the energy levels above the surface. The resulting Φ were further used to calculate the theoretical half-cell electrode potential for the slabs, for each coverage state, as outlined in the seminal paper by Trasatti:47
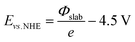 | (2) |
The effect of hydrogen coverage has been further investigated by means of the ab initio thermodynamics formalism50,51 with the objective of elucidating the level of hydrogenation as a function of the chemical potential of H2 in the gas phase. The surface free energies (σ) are therefore defined as follows:
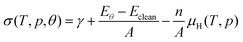 | (3) |
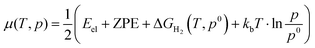 | (4) |
Results and discussion
Our study of the H2 adsorption on these TMCs – TiC, VC, ZrC and NbC – first explored the stability of molecular hydrogen above a test surface, namely the (001) surface of TiC. Initially, H2 was placed 6.5 Å over the (001) surface of TiC and fully optimized, resulting in a weak long-range interaction energy of 0.05 eV. Secondly, the distance between the surface and the molecule was systematically decreased to find potential curves. Spontaneous dissociative chemisorption was observed to occur when the molecule was placed less than 2.0 Å above the topmost surface atomic plane. The dissociation happens on top of one of the surface Ti atoms, producing an intermediate in which one of hydrogens is coordinated by two Ti atoms and the other absorbs on top of a C atom. However, the most favourable adsorption is found when both H atoms absorb on top of a surface C, a feature that, as shown below, is shared by all tested systems. The same protocol was subsequently repeated on other low index surfaces as well as on other carbides leading to similar results. For full details of the hydrogen adsorption potential energy surface, please see ESI.†This result agrees with previous experimental and computational results, which show that hydrogen adsorption is dissociative on these carbides.9,52,53
Hydrogen adsorption
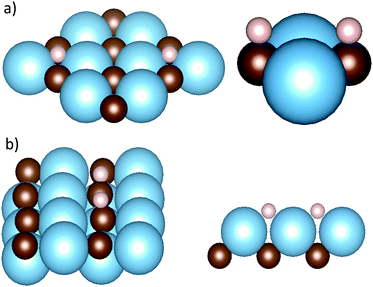
Having established the fundamental exothermicity of adsorption, adsorption sites and their respective energies were explored on all carbides. The results show clear geometric and energetical similarities between each surface plane amongst the four studied carbides. Two different adsorption geometries for the (001) surface are shown in Fig. 1; in the first the adsorbed hydrogens are located on top of a C atom (Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top site) and in the second between two metal atoms (M2-hollow site). On TiC, in the Con
top site) and in the second between two metal atoms (M2-hollow site). On TiC, in the Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top site, each H atom absorbs 1.28 Å above the surface, while on the M2-hollow site, the H absorbs directly above the surface Ti. In the first case, the formation of a C–H bond is combined with a change in M–C bond distance, which increases slightly, as the dangling bonds of C are linked with the electron on hydrogen. However, this elongation is very small. Energetically, the Con
top site, each H atom absorbs 1.28 Å above the surface, while on the M2-hollow site, the H absorbs directly above the surface Ti. In the first case, the formation of a C–H bond is combined with a change in M–C bond distance, which increases slightly, as the dangling bonds of C are linked with the electron on hydrogen. However, this elongation is very small. Energetically, the Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top site is favoured, with ΔEads = −0.62 eV, while the M2-hollow site shows an endothermic adsorption, with ΔEads = +0.38 eV. A Bader charge analysis and a density of states (DOS) calculation have been performed on both the pristine and the hydrogenated surfaces. The two analyses show how the adsorption has little effect on the electronic structure of the surface, and the former also highlights that for both adsorption sites the two adsorbed hydrogens retain one electron each. For further details on the two analyses, see ESI.† Similar results in terms of geometry, surface reconstruction and charge localization were found on all other carbides, as reported in Table 1. Energetically, TiC, VC and ZrC exhibit favourable hydrogen adsorption on their (001) surfaces, while NbC showing endothermic adsorption energies on both the Con
top site is favoured, with ΔEads = −0.62 eV, while the M2-hollow site shows an endothermic adsorption, with ΔEads = +0.38 eV. A Bader charge analysis and a density of states (DOS) calculation have been performed on both the pristine and the hydrogenated surfaces. The two analyses show how the adsorption has little effect on the electronic structure of the surface, and the former also highlights that for both adsorption sites the two adsorbed hydrogens retain one electron each. For further details on the two analyses, see ESI.† Similar results in terms of geometry, surface reconstruction and charge localization were found on all other carbides, as reported in Table 1. Energetically, TiC, VC and ZrC exhibit favourable hydrogen adsorption on their (001) surfaces, while NbC showing endothermic adsorption energies on both the Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top and M2-hollow adsorption sites.
top and M2-hollow adsorption sites.
| Site | ΔEads | Z ads | e − | |
|---|---|---|---|---|
| ΔEads: adsorption energy per atom in eV. Zads: adsorption distance in Å. e−: Bader charge on the adsorbed hydrogen in atomic units. | ||||
| TiC | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top top |
−0.62 | 1.13 | 0.94 |
| VC | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top top |
−0.17 | 1.14 | 0.97 |
| ZrC | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top top |
−0.74 | 1.34 | 1.01 |
| NbC | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top top |
0.06 | 1.12 | 0.97 |
On the (011) surfaces, similar M2-hollow and Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top adsorption sites are found. On such surfaces both sites show higher ΔEads by 0.5–1 eV compared to (001), and the adsorption on the Con
top adsorption sites are found. On such surfaces both sites show higher ΔEads by 0.5–1 eV compared to (001), and the adsorption on the Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top site is again the most exergonic and thus most favourable on these surfaces. Due to the conformation of the surface, the C–H distance for the Con
top site is again the most exergonic and thus most favourable on these surfaces. Due to the conformation of the surface, the C–H distance for the Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top site surface is shorter than that of the same site on (001) and an even smaller M–C bond elongation is found, while on the M2-hollow site adsorbed hydrogen is at a greater distance from the surface. The distortion of the surface also causes the hydrogen atoms on the Con
top site surface is shorter than that of the same site on (001) and an even smaller M–C bond elongation is found, while on the M2-hollow site adsorbed hydrogen is at a greater distance from the surface. The distortion of the surface also causes the hydrogen atoms on the Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top site not to be vertically aligned with their respective carbon. The Bader charge analysis shows an equal localization of the charge between the two atoms, which as in the previous case retain their respective electrons. Table 2 shows the adsorption energies, Bader charges on hydrogens and C–H bond distances on the (011) surfaces of all four carbides.
top site not to be vertically aligned with their respective carbon. The Bader charge analysis shows an equal localization of the charge between the two atoms, which as in the previous case retain their respective electrons. Table 2 shows the adsorption energies, Bader charges on hydrogens and C–H bond distances on the (011) surfaces of all four carbides.
| Site | ΔEads | Z ads | e − | |
|---|---|---|---|---|
| ΔEads: adsorption energy per atom in eV. Zads: adsorption distance in Å. e−: Bader charge on the adsorbed hydrogen in atomic units. | ||||
| TiC | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top top |
−1.40 | 1.12 | 1.03 |
| VC | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top top |
−1.07 | 1.11 | 0.93 |
| ZrC | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top top |
−1.36 | 1.06 | 1.12 |
| NbC | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top top |
−0.88 | 1.11 | 0.89 |
The two surface terminations along the (111) plane are treated separately because of the variation in the stoichiometries of their topmost atomic layer and their resulting different surface energies. Both the metal- and carbon-terminated slab models show a dipole perpendicular to the surface, arising from the presence of alternate layers of carbon and metal atoms.54 However, previous studies have shown similar trends in the electronic properties of the surface on both reconstructed and unreconstructed surfaces.36 Moreover, experimental reports only show unreconstructed metal-terminated surfaces for the (111) plane, when this surface can be shown to be clean and free of impurities under ultravacuum conditions.55–58 For these reasons, only the unreconstructed metal and carbon terminations of the (111) plane will be considered in this study.
On the metal-terminated (111) plane – (111)-M from now on – the surface atoms are arranged in a hexagonal fashion, as shown in Fig. 2. A threefold site is available for the hydrogen, which adsorbs at the barycentre of a triangle formed by 3 metal atoms, and on top of a carbon atom of the second layer of the slab, labelled as M3-hollow site. This configuration involves large adsorption energies on all carbides, up to ΔEads = −1.99 eV on TiC. The electron-donating nature of the terminating metal layer is made clear by a Bader charge analysis of the slab, which shows 1.6 e− on the hydrogens upon homolytic cleavage. The ΔEads values for all carbides and other parameters of interest related to the adsorption are reported in Table 3.
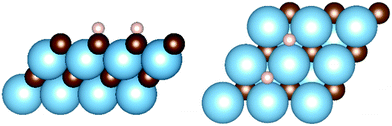 | ||
Fig. 2 Adsorption geometries for (111) surfaces: M3-hollow site on the metal terminated surface (right) and Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top site on the carbon terminated surface (left). top site on the carbon terminated surface (left). | ||
| Site | ΔEads | Z ads | e − | |
|---|---|---|---|---|
| ΔEads: adsorption energy per atom in eV. Zads: adsorption distance in Å. e−: Bader charge on the adsorbed hydrogen in atomic units. | ||||
| TiC | M3-hollow | −1.99 | 2.02 | 1.64 |
| VC | M3-hollow | −1.17 | 1.94 | 1.56 |
| ZrC | M3-hollow | −1.34 | 2.17 | 1.68 |
| NbC | M3-hollow | −1.24 | 2.07 | 1.59 |
A different picture emerges from the calculations on the (111)-C surface. This surface termination shows instability in the presence of hydrogen, leading to a dramatic reconstruction on TiC and VC, whereby a combination of carbon atom sintering and hydro-carbon formation distorts the pristine surface geometries. However, for the two 5th period TMCs in this study, it was possible to find a minimum in the potential energy surface associated with the adsorption. In the latter cases the adsorbed hydrogen absorbs on a Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top site, similarly to that found on the (001) and (011) surfaces. However, a more exothermic reaction and a more extensive surface reconstruction of the model slab are involved. Table 4 summarizes these results, which are consistent with the previously reported energetic preference for metal termination on the (111) surface of these two carbides, as deduced from surface energies.36
top site, similarly to that found on the (001) and (011) surfaces. However, a more exothermic reaction and a more extensive surface reconstruction of the model slab are involved. Table 4 summarizes these results, which are consistent with the previously reported energetic preference for metal termination on the (111) surface of these two carbides, as deduced from surface energies.36
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top binding of molecular hydrogen on the (111)-C surfaces
top binding of molecular hydrogen on the (111)-C surfaces
| Site | ΔEads | Z ads | e − | |
|---|---|---|---|---|
| ΔEads: adsorption energy per atom in eV. Zads: adsorption distance in Å. e−: Bader charge on the adsorbed hydrogen in atomic units. | ||||
| TiC | N/D | — | — | — |
| VC | N/D | — | — | — |
| ZrC | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top top |
−2.01 | 1.10 | 0.88 |
| NbC | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top top |
−1.69 | 1.10 | 0.83 |
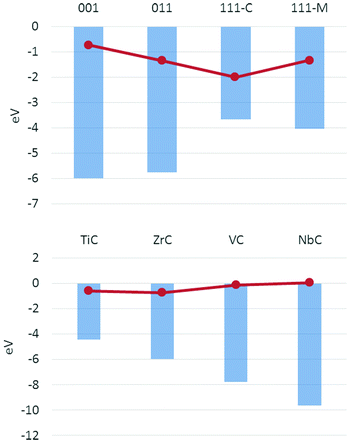
The binding energies obtained for hydrogen adsorption can be compared with previous studies on the same surfaces,36 highlighting correlations between the surface properties and their reactivity. The reported surface energies and d-band positions for these materials show trends along the rows and down the groups that correlate well to their reactivity. The trends over the surfaces for a single carbide and over the same face of each carbide show an inverse correlation with the ΔEads which, despite some discrepancies, can be considered a good descriptor of the activity of the carbide surface considered. Fig. 3 shows how, for the (001) surfaces of all carbides as well as all four surfaces of ZrC, a less negative d-band centre corresponds to a more exothermic hydrogen adsorption.
Higher hydrogen loadings
In this section, our approach is to load hydrogen atoms up to monolayer (ML) coverage. In the previous section, 16 adsorption sites had been identified on each model slab: on the slab representing (001) and (011) surfaces these are equally divided between Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top and M2-hollow, while on those representing the two terminations of the (111) surfaces either 16 Con
top and M2-hollow, while on those representing the two terminations of the (111) surfaces either 16 Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top or 16 M3-hollow sites are present. Therefore, loadings of 4, 8 and 16 hydrogen atoms over the 16 surface adsorption sites are investigated, and the corresponding coverage and surface properties are then evaluated for each system.
top or 16 M3-hollow sites are present. Therefore, loadings of 4, 8 and 16 hydrogen atoms over the 16 surface adsorption sites are investigated, and the corresponding coverage and surface properties are then evaluated for each system.
On the (001) surface termination, adsorption of 4 and 8 H produces a decrease in adsorption energy per atom on each of the four carbides in study. The adsorbed hydrogens all absorb on the 8 Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top sites. Subsequent adsorption of H2 on the surface is expected to occur on the M2-hollow site, which has been shown previously to be endothermic. However, steric effects prevent these sites from being available. Thus we find that on the carbides of the 5th period, ZrC and NbC, hydrogen adsorbs on the more endothermic Mon
top sites. Subsequent adsorption of H2 on the surface is expected to occur on the M2-hollow site, which has been shown previously to be endothermic. However, steric effects prevent these sites from being available. Thus we find that on the carbides of the 5th period, ZrC and NbC, hydrogen adsorbs on the more endothermic Mon![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top sites, resulting in a positive total adsorption energy (see Table 5 and Fig. 4). On the carbides of the 4th period, TiC and VC, it was not possible to find a stable minimum for the adsorption on such sites for the (001) surface.
top sites, resulting in a positive total adsorption energy (see Table 5 and Fig. 4). On the carbides of the 4th period, TiC and VC, it was not possible to find a stable minimum for the adsorption on such sites for the (001) surface.
| nH | θ | Site | TiC | VC | ZrC | NbC |
|---|---|---|---|---|---|---|
| nH: number of H atoms on the surface of the slab. θ: coverage, as a fraction of a monolayer. TiC, VC, ZrC, NbC: ΔEads on each carbide in eV. | ||||||
| 2 | ¼ | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top top |
−0.62 | −0.17 | −0.73 | +0.06 |
| 4 | ½ | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top top |
−0.52 | −0.14 | −0.62 | +0.04 |
| 8 | 1 | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top top |
−0.35 | −0.06 | −0.38 | +0.09 |
| 16 | 2 | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top + Mon top + Mon![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top top |
— | — | +0.09 | +0.31 |
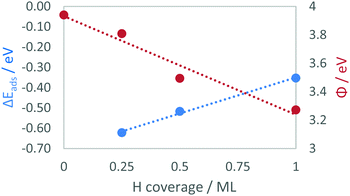 | ||
| Fig. 4 The graph shows the correlation between hydrogen loading and ΔEads (blue) and between hydrogen loading and Φ (red) on the TiC(001) surface. | ||
For these reasons we consider that the chemisorption of H on Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top defines the monolayer on all (001) surfaces in our study, even if these are only half of the stable minima found on the potential energy surface for chemisorbed hydrogen. Within our model slabs, this translates in having θ = 1 when 8 H atoms are adsorbed.
top defines the monolayer on all (001) surfaces in our study, even if these are only half of the stable minima found on the potential energy surface for chemisorbed hydrogen. Within our model slabs, this translates in having θ = 1 when 8 H atoms are adsorbed.
For all four carbides, the increase in coverage leads to a decrease in the adsorption energy per atom, which is consistent with the results found for other carbides by previous work.59 This effect is not unexpected, and insight comes from the analysis of the work function (Φ), which steadily decreases with coverage as electrons are inserted in the conduction band (Fig. 4). As highlighted in previous literature,49,60Φ can be correlated with the open circuit half-cell potential. We therefore used eqn (2) to convert the Φ values into potential values against the NHE. Such a conversion highlights how the potential decreases slightly with coverage. In particular, the voltage difference between pristine surface and the first adsorbed molecule is only 0.13 V, suggesting by reversing the relationship, how a small change in potential might influence the adsorption and desorption of H2 on these surfaces.
The trends in adsorption energy, work function and theoretical Vhalf![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cell with θ are found to be similar on all the investigated carbides and surfaces. As shown in Table 5, adsorption up to the monolayer is exothermic on all investigated carbides which showed exothermic adsorption for a single molecule.
cell with θ are found to be similar on all the investigated carbides and surfaces. As shown in Table 5, adsorption up to the monolayer is exothermic on all investigated carbides which showed exothermic adsorption for a single molecule.
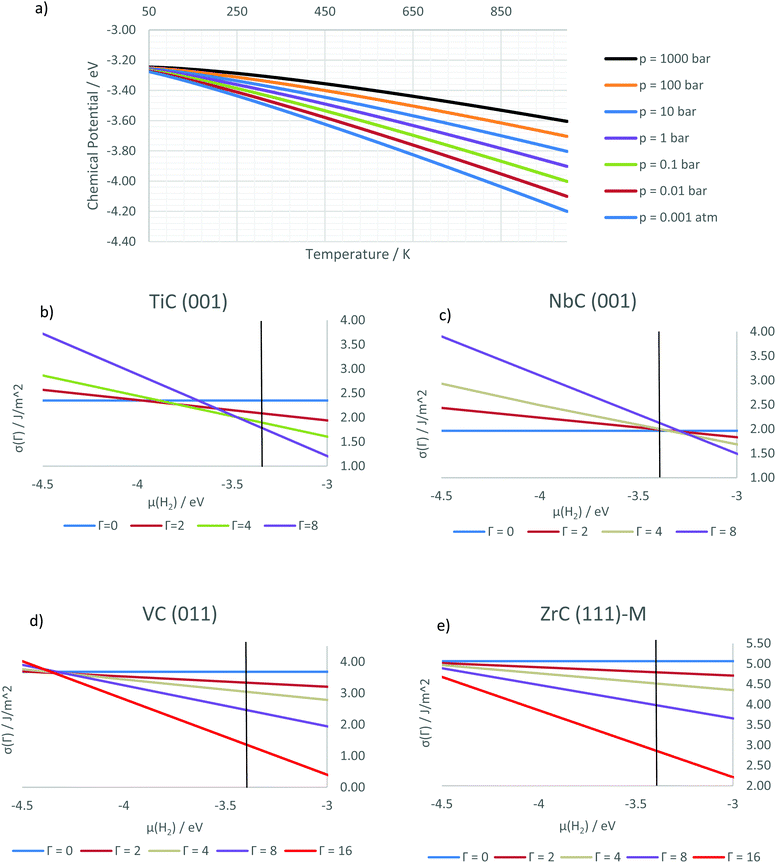
To elucidate the relationship between the different coverage conditions we computed the surface free energies of the hydrogenated surfaces. Fig. 5b shows the surface free energies for the four stable coverages of the TiC(001) surface versus the chemical potential of the hydrogen, whose dependency on temperature and pressure is shown in Fig. 5a. The graph highlights how lower coverages are expected to be more favourable for low chemical potentials. The vertical black line on the graph refers to the conditions of standard temperature and pressure, highlighting how these correspond to a fully hydrogenated surface, a property shared with every other investigated surface apart from the (001) surface of NbC, shown in Fig. 5c: on this surface, the increase in electronic energy as a result of the hydrogen adsorption results in a clean surface in standard conditions. However, both partial and full coverage are observed at higher chemical potentials, occurring at high pressures or low temperatures.
It is possible to correlate the catalytic activity of a material towards the hydrogen evolution reaction (HER) with the free energy of adsorption of hydrogen on its surface, which has to be close to zero to achieve the best catalytic activity.61 This is because the reaction is composed of two separate steps, of which the adsorbed hydrogen is the necessary intermediate: at equilibrium the initial and final step will have the same free energy. Therefore, we can predict the conditions at which the reaction will be most efficiently catalysed by identifying the intersections between the lines representing two subsequent coverage states. On TiC(001) this would imply having the best catalytic activity at temperatures higher than 300 K, while on NbC(001) low temperatures or high pressures are needed to catalyse the reaction efficiently. As highlighted above, the graphs for VC(001) and ZrC(001) are similar to that of TiC(001), but due to the less exothermic ΔEads values, the equilibrium states between different coverage states for VC(001) are closer to 298 K and 1 atm.
Similar trends are found on the (011) surfaces as a function of θ, showing a decrease in ΔEads, Φ and Vhalf![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cell, as shown in Table 6. However, owing to the larger interatomic spacing on the (011) surfaces, the 8 M2-hollow sites are still available after all 8 Con
cell, as shown in Table 6. However, owing to the larger interatomic spacing on the (011) surfaces, the 8 M2-hollow sites are still available after all 8 Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top sites are filled. As seen for the loading of a single molecule, the adsorption is exothermic on these sites, although less than the Con
top sites are filled. As seen for the loading of a single molecule, the adsorption is exothermic on these sites, although less than the Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top sites.
top sites.
| nH | θ | Site | TiC | VC | ZrC | NbC |
|---|---|---|---|---|---|---|
| nH: number of H atoms on the surface of the slab. θ: coverage, as a fraction of a monolayer. TiC, VC, ZrC, NbC: ΔEads on each carbide in eV. | ||||||
| 2 | ⅛ | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top top |
−1.40 | −1.07 | −1.36 | −0.88 |
| 4 | ¼ | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top top |
−1.29 | −0.98 | −1.35 | −0.88 |
| 8 | ½ | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top top |
−1.25 | −0.94 | −1.26 | −0.79 |
| 16 | 1 | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top + M2-hollow top + M2-hollow |
−0.84 | −0.64 | −0.93 | −0.71 |
The condition of full coverage on the studied (011) surfaces can therefore entail the filling of all metal and carbon sites, corresponding to 16 chemisorbed H atoms on 16 available adsorption sites in our model slabs. The calculated surface free energies show that such coverage is the most favourable for all but the most negative chemical potentials, corresponding to very high temperatures and low pressures (as shown in Fig. 5d for VC). We can therefore predict that these will be the conditions at which the (011) surfaces of the four carbides in our study will show HER activity, since less extreme conditions show strong bias towards the highest possible coverage. This effect is due to the larger ΔEads found on the (011) surfaces, which make the adsorption favourable in all but the most extreme cases.
The (111) surfaces have 16 equal adsorption sites on each slab, either Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top or M3-hollow depending on surface termination. On the metal termination, the adsorption is repeated without changes in geometry as hydrogen loading increases, which is followed by the expected decrease in ΔEads, as shown in Table 7. On the carbon termination, higher loadings of hydrogen markedly stabilize the surface, revealing stable configurations for TiC and VC for 16/16 and 4/16 occupied adsorption sites, respectively, while keeping the reaction very exothermic for all coverages and carbides, as highlighted in Table 7.
top or M3-hollow depending on surface termination. On the metal termination, the adsorption is repeated without changes in geometry as hydrogen loading increases, which is followed by the expected decrease in ΔEads, as shown in Table 7. On the carbon termination, higher loadings of hydrogen markedly stabilize the surface, revealing stable configurations for TiC and VC for 16/16 and 4/16 occupied adsorption sites, respectively, while keeping the reaction very exothermic for all coverages and carbides, as highlighted in Table 7.
| nH | θ | Site | TiC | VC | ZrC | NbC |
|---|---|---|---|---|---|---|
| nH: number of H atoms on the surface of the slab. θ: coverage, as a fraction of a monolayer. TiC, VC, ZrC, NbC: ΔEads on each carbide in eV. | ||||||
| 2 | ⅛ | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top top |
−1.96 | −1.17 | −1.33 | −1.24 |
| 4 | ¼ | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top top |
−1.67 | −1.14 | −1.34 | −1.22 |
| 8 | ½ | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top top |
−1.44 | −1.08 | −1.33 | −1.16 |
| 16 | 1 | Con![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) top top |
−1.36 | −1.01 | −1.35 | −1.11 |
| 2 | ⅛ | M3-hollow | — | — | −2.01 | −1.69 |
| 4 | ¼ | M3-hollow | — | −1.68 | −2.01 | −1.69 |
| 8 | ½ | M3-hollow | — | −1.64 | −1.96 | −1.62 |
| 16 | 1 | M3-hollow | −1.93 | −1.55 | −1.83 | −1.45 |
Calculating the free energies for these surfaces produces similar results for all the investigated metal carbides. Owing to the high ΔEads, hydrogens fill the adsorption sites (coverage = 1 ML) on both terminations. This result means that, in the phase space we have explored, these carbides are not likely to favour hydrogen desorption and will therefore exhibit poor catalytic activity toward the HER reaction on their (111) surfaces. This is exemplified by Fig. 5e, which shows the corresponding plot for ZrC(111)-M.
The calculations on the hydrogenated surfaces in this study have shown a strong dependence of the energetics of the reaction on both the surface and the material. Overall, it was possible to identify several trends from the data analysed. The Con-top is the preferred adsorption site, where the process is always exothermic except for NbC(001). Metal sites are less favourable on all surfaces, but show a stronger interaction as the number of coordinated metals increases, so that the M3-hollow sites allow a strong adsorption of the hydrogen on (111) surfaces. On both carbon and metal sites the energetic trends and adsorption properties on the four surfaces studied are consistent across the four carbides, showing very similar trends. For all surfaces and coverages, reaction on VC and NbC corresponds to less exothermic adsorption energies with respect to the same reactions over TiC and ZrC, showing a clear effect of the group in the periodic table.
The effect of the row is less marked, but in some cases the reduced lattice parameter for the carbides of the 4th row induces steric effects that hinder the adsorption. These trends could be in some cases related to the electronic characteristics of the surfaces. The low Φ of TiC and ZrC is in relation to their higher activities, as are the d-band centres for all surfaces, which have been proven to show a useful correlation with the activity of the material over the hydrogen adsorption and could therefore be used as descriptors. Similarly, the effect of coverage is clearly correlated with a drop in both ΔEads and Φ: as more hydrogens are added on a surface, more electrons are added to the conduction band of the solid, thereby obstructing further hydrogenation of the slab. However, the highest coverage is consistently the most exothermic across all surfaces, apart from the already mentioned NbC(001), as the decrease in exothermicity with coverage is small compared to the total value of adsorption energy, especially for (011) and (111) surfaces. For this reason, such surfaces are predicted to show less catalytic activity towards the hydrogen evolution reaction than (001) surfaces which show less exothermic ΔEads values.
Summary
We have presented a comprehensive DFT study into hydrogen adsorption on the four low index surfaces of TiC, VC, ZrC and NbC. The adsorption is shown to occur primarily on carbon sites and on the most highly coordinated metal sites on the surface. We have demonstrated that all carbides show the same trends across their four surfaces. For each carbide the most exothermic adsorption is found on the (111) surfaces; however, the carbon termination of this surface proved to be very unstable on TiC and VC. The only non-exothermic adsorption is found on the NbC(001) surface. On increasing the amount of hydrogen loading on each of the selected surfaces we found a corresponding decrease in adsorption energy per atom, linked with a similar decrease in the work function of the surface. Although the full coverage is always connected to a lower total energy, the actual coverage of the surface has been found to be generally depended on temperature and pressure of the environment. Using ab initio thermodynamics we were able to predict that the (001) surfaces of the four carbides in the study show the most promise as catalysts for the HER, as the change in coverage states with hydrogen chemical potential is linked to thermodynamic equilibrium between hydrogen adsorption and desorption, a necessary condition for catalysis over HER.Although these findings help our understanding of the interaction between transition metal carbides and hydrogen, future work is needed both experimentally, to prove those findings, and theoretically, to investigate the consequences of the observed trends, including the feasibility of CO2 reduction over the surfaces of these carbides.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
FS thanks the Cardiff University School of Chemistry for a fully funded PhD scholarship. This work was funded as part of an EPSRC low carbon fuels grant (EP/N009533/1). Computing facilities for this work were provided by ARCCA at Cardiff University, HPC Wales, and through our membership of the UK's Materials Chemistry Consortium (MCC). The MCC is funded by EPSRC (EP/F067496). Information on the data underpinning the results presented here, including how to access them, can be found in the Cardiff University data catalogue at http://doi.org/10.17035/d.2018.0064126200.Notes and references
- R. Nakicenovic and N. Swart, Intergovenmental Panel on Climate Change, Washington, DC, 2014 Search PubMed.
- Fourth National Climate Assessment, Vol. I: the Climate Science Special Report, US Department of Energy, 2017.
- N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735 CrossRef CAS PubMed.
- C. Ling, L. Shi, Y. Ouyang and J. Wang, Chem. Mater., 2016, 28, 9026–9032 CrossRef CAS.
- B. E. Conway and B. V. Tilak, Electrochim. Acta, 2002, 47, 3571–3594 CrossRef CAS.
- W. Cui, Q. Liu, N. Cheng, A. M. Asiri and X. Sun, Chem. Commun., 2014, 50, 9340–9342 RSC.
- X. Guo, G. Cao, F. Ding, X. Li, S. Zhen, Y. Xue, Y. Yan, T. Liu and K. Sun, J. Mater. Chem. A, 2015, 3, 5041–5046 RSC.
- K. Z. Qi, G. C. Wang and W. J. Zheng, Surf. Sci., 2013, 614, 53–63 CrossRef CAS.
- W.-F. Chen, J. T. Muckerman and E. Fujita, Chem. Commun., 2013, 49, 8896 RSC.
- K. Oshikawa, M. Nagai and S. Omi, J. Phys. Chem. B, 2001, 105, 9124–9131 CrossRef CAS.
- A. L. Stottlemyer, T. G. Kelly, Q. Meng and J. G. Chen, Surf. Sci. Rep., 2012, 67, 201–232 CrossRef CAS.
- R. B. Levy and M. Boudart, Science, 1973, 181, 547–549 CrossRef CAS PubMed.
- J. Häglund, A. Fernndez Guillermet, G. Grimvall and M. Körling, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 11685–11691 CrossRef.
- L. Toth, Transition Metal Carbides and Nitrides, Academic Press, New York and London, 1971 Search PubMed.
- A. Neckel, P. Rastl, R. Eibler, P. Weinberger and K. Schwarz, J. Phys. C: Solid State Phys., 2001, 9, 579–592 CrossRef.
- A. Kelly and D. Rowcliffe, Phys. Status Solidi, 1966, 14, K29–K33 CrossRef CAS.
- X. Fan, B. Chen, M. Zhang, D. Li, Z. Liu and C. Xiao, Mater. Des., 2016, 112, 282–289 CrossRef CAS.
- D. W. Lee, S. V. Alexandrovskii and B. K. Kim, Mater. Lett., 2004, 58, 1471–1474 CrossRef CAS.
- S. Tjong, Mater. Sci. Eng., R, 2000, 29, 49–113 CrossRef.
- P. S. Henderson, Surf. Coat. Technol., 2003, 174–175, 720–724 Search PubMed.
- W. Yang, S. Rehman, X. Chu, Y. Hou and S. Gao, ChemNanoMat, 2015, 13, 76–398 Search PubMed.
- S. R. Shatynski, Oxid. Met., 1979, 13, 105–118 CrossRef CAS.
- H. H. Hwu and J. G. Chen, Chem. Rev., 2005, 105, 185–212 CrossRef CAS PubMed.
- F. Vines, C. Sousa, P. Liu, J. A. Rodriguez and F. Illas, J. Chem. Phys., 2005, 122, 174709 CrossRef CAS PubMed.
- L. Ramqvist, K. Hamrin, G. Johansson, A. Fahlman and C. Nordling, J. Phys. Chem. Solids, 1969, 30, 1835–1847 CrossRef CAS.
- K. Schwarz, Crit. Rev. Solid State Mater. Sci., 1987, 13, 211–257 CrossRef CAS.
- L. Delannoy, J. M. Giraudon, P. Granger, L. Leclercq and G. Leclercq, Catal. Today, 2000, 59, 231–240 CrossRef CAS.
- L. K. Ono, D. Sudfeld and B. Roldan Cuenya, Surf. Sci., 2006, 600, 5041–5050 CrossRef CAS.
- C. Kunkel, F. Viñes and F. Illas, Energy Environ. Sci., 2016, 9, 141–144 RSC.
- S. Posada-Pérez, F. Viñes, P. J. Ramirez, A. B. Vidal, J. A. Rodriguez and F. Illas, Phys. Chem. Chem. Phys., 2014, 16, 14912–14921 RSC.
- M. D. Porosoff, S. Kattel, W. Li, P. Liu and J. G. Chen, Chem. Commun., 2015, 51, 6988–6991 RSC.
- M. D. Porosoff, X. Yang, J. A. Boscoboinik and J. G. Chen, Angew. Chem., Int. Ed., 2014, 53, 6705–6709 CrossRef CAS PubMed.
- D. V. Esposito, S. T. Hunt, A. L. Stottlemyer, K. D. Dobson, B. E. Mccandless, R. W. Birkmire and J. G. Chen, Angew. Chem., 2010, 9859–9862 CrossRef CAS PubMed.
- A. L. Tomás-García, J. O. Jensen, N. J. Bjerrum and Q. Li, Electrochim. Acta, 2014, 137, 639–646 CrossRef.
- T. Xiao, A. P. E. York, K. S. Coleman, J. B. Claridge, J. Sloan, J. Charnock and M. L. H. Green, J. Mater. Chem., 2001, 11, 3094–3098 RSC.
- M. G. Quesne, A. Roldan, N. H. de Leeuw and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2018, 20, 6905–6916 RSC.
- G. Kresse and J. Furthmiiller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233 CrossRef.
- R. F. Bader, Atoms in molecules: a quantum theory, International series of monographs on chemistry, 1990, vol. 22 Search PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- S. Trasatti, Electrochim. Acta, 1991, 36, 1659–1667 CrossRef CAS.
- E. Skúlason, G. S. Karlberg, J. Rossmeisl, T. Bligaard, J. Greeley, H. Jónsson and J. K. Nørskov, Phys. Chem. Chem. Phys., 2007, 9, 3241–3250 RSC.
- J. Rossmeisl, E. Skúlason, M. E. Björketun, V. Tripkovic and J. K. Nørskov, Chem. Phys. Lett., 2008, 466, 68–71 CrossRef CAS.
- X.-G. Wang, W. Weiss, S. K. Shaikhutdinov, M. Ritter, M. Petersen, F. Wagner, R. Schogl and M. Scheffl, Phys. Rev. Lett., 1998, 81, 1038 CrossRef CAS.
- D. Santos-Carballal, A. Roldan, R. Grau-Crespo and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2014, 16, 21082–21097 RSC.
- Y. Zhao, A. C. Dillon, Y. H. Kim, M. J. Heben and S. B. Zhang, Chem. Phys. Lett., 2006, 425, 273–277 CrossRef CAS.
- S. Trasatti, J. Electroanal. Chem., 1972, 39, 163–184 CrossRef CAS.
- P. W. Tasker, J. Phys. C: Solid State Phys., 1979, 12, 4977–4984 CrossRef CAS.
- T. Aizawa, W. Hayami, R. Souda, S. Otani and Y. Ishizawa, Surf. Sci., 1997, 381, 157–164 CrossRef CAS.
- W. Hayami, R. Souda, T. Aizawa, S. Otani and Y. Ishizawa, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 13752–13758 CrossRef CAS.
- R. Souda, T. Aizawa, S. Otani and Y. Ishizawa, Surf. Sci., 1990, 232, 219–227 CrossRef CAS.
- W. Hayami, et al. , Surf. Sci., 1992, 276, 299–307 CrossRef CAS.
- S. Posada-Pérez, F. Viñes, R. Valero, J. A. Rodriguez and F. Illas, Surf. Sci., 2017, 656, 24–32 CrossRef.
- V. Tripkovic, M. E. Björketun, E. Skúlason and J. Rossmeisl, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 115452 CrossRef.
- J. K. Norskov, J. Electrochem. Soc., 2005, 152, J23–J26 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp05975f |
| This journal is © the Owner Societies 2019 |