Solving the Schrödinger equation of hydrogen molecules with the free-complement variational theory: essentially exact potential curves and vibrational levels of the ground and excited states of the Σ symmetry†
Abstract
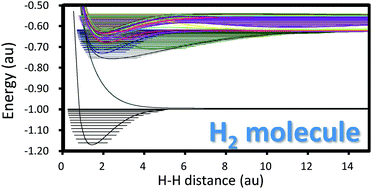
The Schrödinger equation of hydrogen molecules was solved essentially exactly and systematically for calculating the potential energy curves of the electronic ground and excited states of the 1Σg, 1Σu, 3Σg, and 3Σu symmetries. The basic theory is the variational free complement theory, which is an exact general theory for solving the Schrödinger equation of atoms and molecules. The results are essentially exact with the absolute energies being correct beyond μ-hartree digits. Furthermore, all of the present wave functions satisfy correct orthogonalities and Hamiltonian-orthogonalities to each other at every nuclear distance along the potential curve, which makes systematic analyses and discussions possible among all the calculated electronic states. It is noteworthy that these conditions were not satisfied in many of the accurate calculations of H2 reported so far. Based on the present essentially exact potential curves, we calculated and analyzed the vibrational energy levels associated with all the electronic states. Among them, the excited states having double-well potentials showed some interesting features of the vibrational states. These results are worthy of future investigations in astronomical studies.
- This article is part of the themed collection: 2018 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...