Mineralization of phosphorylated cellulose: crucial role of surface structure and monovalent ions for optimizing calcium content†
Abstract
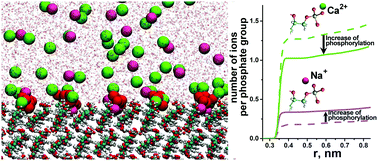
Cellulose can be phosphorylated to produce organic matrices with highly adsorptive properties for, e.g., biocompatible materials for biomedical applications. We focus on the effects of phosphorylation of surfaces of crystalline nanocellulose and, in particular, on the competitive adsorption of mono- and divalent cations (Na+ and Ca2+) typically contained in mineralizing salt mixtures using all-atom molecular dynamics (MD) simulations. Phosphorylation was applied at 12% and 25% both in water and CaCl2 solutions. Our main result shows that Na+ and Ca2+ cations are concentrated in different interfacial layers with Na+ ions penetrating much closer to the surface. This behavior cannot be described by the Poisson–Boltzmann theory or implicit solvent simulations. Our analysis shows that the physical origin of this observation is due to a balance between the electrostatic interactions and hydration free energy associated with the ions. Adsorption levels of the different ions also respond differently to changes in the degree of phosphorylation. We show that the number of adsorbed Na+ ions per phosphate group increases whereas the number of adsorbed Ca2+ ions decreases with an increasing degree of phosphorylation (or when the number of binding sites increases). The decrease in the number of adsorbed Ca2+ ions can be explained by an increasing “charge–charge” repulsion between the Ca2+ ions attracted by the charged surface. Importantly, our results demonstrate the existence of an optimum degree of phosphorylation in terms of adsorbed Ca2+ ions and can be used as a guideline in materials design, for example, when choosing the cellulose matrix or with other similarly structured biomolecular and polymer surfaces.
- This article is part of the themed collection: 2018 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...