Molecular dynamics investigation of the local structure in iron melts and its role in crystal nucleation during rapid solidification
Abstract
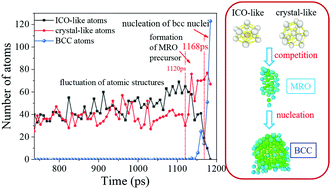
A comprehensive investigation on local structures in iron melts and their role in nucleation under various cooling rates was performed by means of large-scale molecular dynamics simulations. The embedded atoms method (EAM) was adopted to describe the interactions between iron atoms. Connections between short-range order (SRO), medium-range order (MRO), and crystalline nucleation from iron melts were constructed using several structural analysis techniques, including the radial distribution function, common neighbor analysis method, the Voronoi tessellation, and bond order analysis. The simulation results showed that abundant types of atomic clusters with SRO, mainly including the icosahedral-like (ICO-like) and fcc-like clusters, were predominant in undercooled iron melts. The obtained microstructures were determined by the competition between the ICO-like and crystal-like configurations. There existed a critical cooling rate, below which the fcc-like configurations gain the advantage upon cooling and where crystallization could take place; otherwise, the ICO-like configurations are favored and the glass phases could be obtained. Furthermore, it was proved that the crystal nucleation could be divided into three stages: first, a fluctuation and competition between crystal-like and ICO-like clusters in undercooled melts; second, the formation and growth of MRO clusters via the transformation of atomic configurations from ICO-like to crystal-like; finally, the nucleation of bcc nuclei from the core of steady MRO clusters. This process agrees with the Ostwald's step rule and the findings from other investigations. Based on the analysis of the compositional origin of MRO clusters, we further found that the MRO clusters were mainly composed of fcc-like instead of ICO-like configurations, indicating a negative role of ICO-like configurations in crystal nucleation.
- This article is part of the themed collection: 2018 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...