Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Prediction of self-assembly of adenosine analogues in solution: a computational approach validated by isothermal titration calorimetry†
Luca
Redivo‡
a,
Rozalia-Maria
Anastasiadi‡
a,
Marco
Pividori
b,
Federico
Berti
c,
Maria
Peressi
 d,
Devis
Di Tommaso
d,
Devis
Di Tommaso
 *a and
Marina
Resmini
*a and
Marina
Resmini
 *a
*a
aSchool of Biological and Chemical Sciences, Queen Mary University of London, Mile End Road, London, E1 4NS, UK. E-mail: d.ditommaso@qmul.ac.uk; m.resmini@qmul.ac.uk
bDipartimento di Fisica, Università degli Studi di Trieste, via A. Valerio 2, 34149, Trieste, Italy
cDipartimento di Scienze Chimiche e Farmaceutiche, Università degli Studi di Trieste, via L. Giorgieri 1, Trieste, 34149, Italy
dIstituto Officina dei Materiali, Consiglio Nazionale delle Ricerche, S. S. 14 km 163.5, Trieste, Italy
First published on 15th January 2019
Abstract
The recent discovery of the role of adenosine-analogues as neuroprotectants and cognitive enhancers has sparked interest in these molecules as new therapeutic drugs. Understanding the behavior of these molecules in solution and predicting their ability to self-assemble will accelerate new discoveries. We propose a computational approach based on density functional theory, a polarizable continuum solvation description of the aqueous environment, and an efficient search procedure to probe the potential energy surface, to determine the structure and thermodynamic stability of molecular clusters of adenosine analogues in solution, using caffeine as a model. The method was validated as a tool for the prediction of the impact of small structural variations on self-assembly using paraxanthine. The computational results were supported by isothermal titration calorimetry experiments. The thermodynamic parameters enabled the quantification of the actual percentage of dimer present in solution as a function of concentration. The data suggest that both caffeine and paraxanthine are present at concentrations comparable to the ones found in biological samples.
Introduction
Adenosine is a naturally occurring purine nucleoside present in human cells and known to play a key role in a number of pathologies, including neurological disorders, and cardiovascular and autoimmune diseases.1–3 The role of adenosine and its interactions with different receptors have been studied extensively4–6 with consequent interest in adenosine analogues with agonist and antagonist activity7 and methods that allow fast screening.8 Among the different adenosine analogues, caffeine (Fig. 1A) has been the most extensively studied compound. Research carried out on the health implications of caffeine intake has established important beneficial links to a number of illnesses, including depression,9,10 type 2 diabetes, liver disease, Parkinson's disease11 and stroke risk.12 Caffeine is rapidly absorbed in the stomach and it is metabolised to three primary compounds: paraxanthine (82%), theophylline (11%) and theobromine (4%).13–16 Studies have demonstrated that the key physiological effects of caffeine17 are the result of interaction effects on the A1 and A2 subtypes of the adenosine receptor.18 The role of caffeine as a cognitive enhancer19 and also as a neuroprotectant20 have also been reported recently. Caffeine used in combination with melatonin was shown to have antiamyloidogenic action, for the treatment of neurodegenerative diseases.21 Borota et al. have demonstrated recently that caffeine enhances consolidation of long-term memory in humans.22 There is considerable interest in understanding the mechanism by which caffeine and more generally adenosine analogues can interact with different receptors, as this may subsequently lead to the identification of new compounds with drug-like activity. In this context, information on a new molecule's behaviour in solution and its potential for self-assembly, particularly its degree of complexation (i.e. dimers, trimers and tetramers) and the relative distribution, is a key requirement. The self-association of caffeine has been studied experimentally using a variety of techniques including NMR23–25 and FTIR spectroscopies,26 dynamic light scattering (DLS),27,28 osmometry,29 fluorescence,30 thermal analysis and differential scanning calorimetry (DSC).31,32 These methods provide some characterisation although the analysis is often model-dependent. Computational approaches have also been explored to provide a useful tool to understand the behaviour of caffeine. Recent molecular dynamics (MD) simulations of aqueous caffeine solutions by Tavagnacco et al. showed extensive aggregation, with caffeine molecules ‘stacking their flat faces against one another like coins’.33–35 | ||
| Fig. 1 (A) The skeletal chemical structure of caffeine. (B) The most stable dimer structure (D9) in water as calculated using the proposed computational approach. (C) The dimer structure of caffeine as found in the solid state.67,68 For clarity, the reciprocal orientations of the top and bottom molecules in the dimer in (B) and (C) are reported separately. | ||
These simulations were, however, conducted at the limit of solubility of caffeine in water (about 16 mg mL−1) which is approximately five orders of magnitude higher than the concentration range at which caffeine is present in biological systems (0.002 mg mL−1 in plasma).36–38 Such low concentrations would require simulation at the limit of MD techniques, containing hundreds of millions of solvent molecules.
The continuum solvation method is an alternative technique for the determination of the structure and thermodynamic stability of molecular aggregates in solution,39 where the solute (monomer, dimer, trimer, etc.) is treated at the density functional theory (DFT) level and the solvent is described using a polarizable continuum solvation model. Using this approach, Senthilnithy et al.40 and Bradley and Hendson41 report highly positive (+12 kcal mol−1) dimerization free energies. However, the B3LYP density functional employed in these studies does not allow dispersion interactions to be described fully,42 which can affect accuracy. The availability of a computational approach that can accurately predict changes in free energies, because of small structural alterations, would accelerate the identification of new candidate drugs. In this work, we present a quantum mechanical continuum solvation approach as a computational tool that allows prediction of the behaviour in solution of adenosine-analogues (AA) by determining the structure and thermodynamic stability of their molecular clusters (AA)n (n = 2–4), in solution, at concentrations comparable to the ones found in biological samples. Caffeine was initially used as a model molecule; the same tool was then employed to predict the effect of small structural variations in the thermodynamics of molecular aggregation by studying paraxanthine (1,7-dymethylxanthine). The computational approach was then validated experimentally by using isothermal titration calorimetry (ITC), to determine the association enthalpies for both molecules. The thermodynamic data were then used to assess the presence and distribution of potential clusters.
Computational methods
Density functional theory methods
Electronic structure calculations were carried out with the NWChem (version 6.3)43 and Gaussian0944 codes. The B97 density functional together augmented with the D2 Grimme's dispersion correction (B97-D2)45 and the 6-31+G(d,p) basis set46 was chosen to conduct geometry optimization and compute thermal contributions to the gas-phase free energy. The B97-D2 functional was chosen because it is a suitable method to describe molecular complexes with predominant hydrogen-bonding and dispersion contribution.47–50 The 6-31+G(d,p) basis set was chosen because when evaluating binding energies, the addition of diffuse functions on non-hydrogenic atoms to a doubly polarized valence double-ζ basis set provides a good compromise between accuracy and computational cost.51–53 The B97-D2/6-31+G(d,p) method, together with the combination of other functionals and basis sets, was also tested in terms in its ability to locate the “face-to-face” and “face-to-back” dimeric motifs found in the crystallographic structure of caffeine (Section S1, ESI†).The effect of the basis set superposition error (BSSE) was not considered in our simulations. However, the effect of increasing the size of basis set from split-valence double-zeta (6-31+G(d,p)) to split-valence triple-zeta (6-311+G(2df,2p)) on the gas-phase binding energy is only 0.2 kcal mol−1 (Section S2, ESI†). In addition, Di Tommaso and Watson previously demonstrated, using a similar methodology, that the contribution of the BSSE, when evaluated using the counterpoise correction (CPC) method of Boys and Bernardi,55 to the dimerization constant of carboxylic acids in solutionis less than 0.2 unit. Given that the cost of calculating the CPC is higher than that of the original gas-phase interaction energy,56 we have not included this term in the evaluation of the gas-phase energy of caffeine and paraxanthine clusters.
The universal solvation model based on solute electron density (SMD)57 together with the M06-2X density functional52 and the 6-31+G(d,p) basis set was employed to compute the hydration free energies.57 Originally tested over a set of 2892 solvation free energies and transfer free energies for both neutral and ionic species in water and non-aqueous solutions, the mean unsigned error obtained with the SMD model over 26 combinations of various basis sets and density functionals was 0.8 kcal mol−1 for neutral solutes.58
Overall, we expect that the computed Gibbs free energies of a reaction have an uncertainty of ±1.1 kcal mol−1 (Section S2, ESI†). Further calculations to assess the methodology and conduct electron density analysis were also performed using the plane-waves Quantum ESPRESSO59 software suite with the PBE functional with and without dispersion correction and plane-wave basis set cut offs for the smooth part of the wave functions and the augmented density of 28 and 300 Ry, respectively.
Free energies of association in solution
The free energy of formation of caffeine self-associates, (CAF)n (n = 2–4) was computed according to this equation:| ΔGass* = GAB* − GA* − GB* | (1) |
| ΔGD* = ΔGdimer* − 2Gmonomer* | (2) |
The term G* was determined as the sum of the following terms
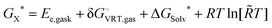 | (3) |
 is the vibrational–rotational–translational contribution to the gas-phase Gibbs free energy at T = 298 K under a standard-state partial pressure of 1 atm, ΔGsolv* is the solvation free energy of the solute corresponding to transfer from an ideal gas at a concentration of 1 mol L−1 to an ideal solution at a liquid-phase concentration of 1 mol L−1, and RT
is the vibrational–rotational–translational contribution to the gas-phase Gibbs free energy at T = 298 K under a standard-state partial pressure of 1 atm, ΔGsolv* is the solvation free energy of the solute corresponding to transfer from an ideal gas at a concentration of 1 mol L−1 to an ideal solution at a liquid-phase concentration of 1 mol L−1, and RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln[
ln[![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) T] is the free energy change of 1 mol of an ideal gas from 1 atm to 1 mol L−1 (RT
T] is the free energy change of 1 mol of an ideal gas from 1 atm to 1 mol L−1 (RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln[
ln[![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) T] = 1.89 kcal mol−1 at T = 298.15 K and
T] = 1.89 kcal mol−1 at T = 298.15 K and ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) = 0.082052 K−1).
= 0.082052 K−1).
The terms Ee,gas and  were computed at the B97-D2/6-31+G(d,p) level of theory, whereas the hydration free energy component, ΔGsolv*, was determined using the SMD/M06-2X/6-31+G(d,p) solvation model using the gas-phase B97-D2/6-31+G(d,p) optimised geometries. Although an approach that includes nuclear relaxation in solution of the solute is supposed to improve a method that uses gas-phase geometries, the hydration free energy (ΔGsolv*) of caffeine calculated as the difference between the solute molecule's energy in solution (SMD/M06-2X/6-31+G(d,p)) at the geometry optimized in gas-phase (B97-D2/6-31+G(d,p)) and the gas phase energy (M06-2X/6-31+G(d,p)) at the geometry optimized in the gas phase (ΔGsolv* = −12.8 kcal mol−1) is in excellent agreement with the experimental value of −12.1 kcal mol−1 (Table S3, ESI†). The value of ΔGsolv* of caffeine changes only slightly if the hydration free energy is calculated as a difference between the caffeine's energy in solution at the geometry optimized in solution and the gas phase free energy at the geometry optimized in the gas phase (ΔGsolv* = −13.2 kcal mol−1) (Table S3, ESI†). This approach also follows the recommendation by Ho et al. that free energies in solution should be obtained from separate gas- and solution-phase calculations,60 because well-established equations based on the statistical thermodynamics of an ideal gas, under the harmonic oscillator rigid rotor approximation, have been developed to calculate gas-phase partition functions and associated thermodynamic functions (entropy, enthalpy and free energy) from the geometries, frequencies, and energies derived from standard ab initio calculations. If a structure is optimised in solution, then the thermal contribution is obtained by applying the same ideal gas partition functions to the frequencies calculated in a dielectric continuum. This approach is questionable because the translational and rotational contributions are unlikely to be valid in solution, and it should only be applied when stationary points in the solution do not correspond to stationary points in the gas-phase.61
were computed at the B97-D2/6-31+G(d,p) level of theory, whereas the hydration free energy component, ΔGsolv*, was determined using the SMD/M06-2X/6-31+G(d,p) solvation model using the gas-phase B97-D2/6-31+G(d,p) optimised geometries. Although an approach that includes nuclear relaxation in solution of the solute is supposed to improve a method that uses gas-phase geometries, the hydration free energy (ΔGsolv*) of caffeine calculated as the difference between the solute molecule's energy in solution (SMD/M06-2X/6-31+G(d,p)) at the geometry optimized in gas-phase (B97-D2/6-31+G(d,p)) and the gas phase energy (M06-2X/6-31+G(d,p)) at the geometry optimized in the gas phase (ΔGsolv* = −12.8 kcal mol−1) is in excellent agreement with the experimental value of −12.1 kcal mol−1 (Table S3, ESI†). The value of ΔGsolv* of caffeine changes only slightly if the hydration free energy is calculated as a difference between the caffeine's energy in solution at the geometry optimized in solution and the gas phase free energy at the geometry optimized in the gas phase (ΔGsolv* = −13.2 kcal mol−1) (Table S3, ESI†). This approach also follows the recommendation by Ho et al. that free energies in solution should be obtained from separate gas- and solution-phase calculations,60 because well-established equations based on the statistical thermodynamics of an ideal gas, under the harmonic oscillator rigid rotor approximation, have been developed to calculate gas-phase partition functions and associated thermodynamic functions (entropy, enthalpy and free energy) from the geometries, frequencies, and energies derived from standard ab initio calculations. If a structure is optimised in solution, then the thermal contribution is obtained by applying the same ideal gas partition functions to the frequencies calculated in a dielectric continuum. This approach is questionable because the translational and rotational contributions are unlikely to be valid in solution, and it should only be applied when stationary points in the solution do not correspond to stationary points in the gas-phase.61
Localisation of energy minima on the PES of dimers
The potential energy surfaces (PESs) of weakly interacting molecular complexes are characterised by a large number of minima. The most stable isomers of the caffeine dimer, (CAF)2, were located using modified version of the computational protocol developed by Di Tommaso and Watson:54 (i) hundreds of thousands of caffeine dimeric configurations were initially generated using the Granada software.62 (ii) A first selection of the caffeine dimers was based on geometrical considerations: only those configurations with caffeine molecules at a distance of less than 4.0 Å were considered for subsequent calculations. (iii) The energies of the configurations generated at step (ii) were computed at the B97-D2/6-31+G(d,p) level of theory and used to calculate the Boltzmann factor (fi):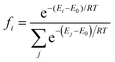 | (4) |
 | (5) |
The procedure to localise minima on the PES of (CAF)2 involved 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 single point energy calculations (∼154k CPU hours using NWChem and 288 cores), followed by 95 structure optimizations (∼13k CPU hours using Gaussian09 and 12 cores), frequency calculation (∼8k CPU hours using Gaussian and 12 cores) and solvation energy evaluation (∼300 CPU hours using Gaussian09 and 12 cores). The total number of CPU hours for the caffeine dimer at the B97-D2/6-31+G(d,p) level of theory was more than 175k CPU hours.
000 single point energy calculations (∼154k CPU hours using NWChem and 288 cores), followed by 95 structure optimizations (∼13k CPU hours using Gaussian09 and 12 cores), frequency calculation (∼8k CPU hours using Gaussian and 12 cores) and solvation energy evaluation (∼300 CPU hours using Gaussian09 and 12 cores). The total number of CPU hours for the caffeine dimer at the B97-D2/6-31+G(d,p) level of theory was more than 175k CPU hours.
Experimental methods
Caffeine (1,3,7-trimethylxanthine) and paraxanthine (1,7-dimethylxanthine) were purchased from Sigma-Aldrich as anhydrous powder. GC grade methanol (Sigma-Aldrich) was employed for recrystallisation. Aqueous solutions were prepared in distilled water. For ITC experiments, the solutions were sonicated, using an ultrasound bath (Sonorex Super BANDELIN electronic GmbH & Co. KG) for 5 min followed by degassing with ThermoVac (MicroCal, Malvern Instruments).X-ray diffraction analysis
Paraxanthine was recrystallized from methanol by slow evaporation at room temperature. A translucent colourless block-like crystal with approximate dimensions of 0.080 × 0.150 × 0.300 mm was used for X-ray crystallographic analysis. A total of 1088 frames were collected. The total exposure time was 3.02 hours. The frames were integrated with the Bruker SAINT software package using a narrow-frame algorithm. Crystal data were collected at 100(2) K: C7H8N4O2, Mr = 180.17, a monoclinic crystal system. The final cell constants of a = 7.376(7) Å, b = 13.329(13) Å, c = 8.193(8) Å, β = 113.50(2)°, volume = 738.7(13) Å3, space group P21/n, Z = 4, calculated = 1.620 g cm−3 and μ = 0.124 mm−1 (Rint = 0.0273) reflections were collected within the 3–28° θ range. The final anisotropic full-matrix least-squares refinement on F2 based on 7147 with I > 2σ(I) and 120 variables converged at R1 = 0.0330 for the observed data, wR2 = 0.0914 for all data and Goodness-of-fit = 1.032.Dissociation experiments by isothermal titration calorimetry
Isothermal titration calorimetry (ITC) measurements were carried out on a VP-ITC Microcalorimeter (MicroCal, Malvern Instruments) at 25 °C. A solution of caffeine (82.4 mM) or paraxanthine (5.55 mM) was loaded in the syringe and step-wise injected in the cell, in degassed H2O. The dilution effect when gradually injecting the concentrated solution of caffeine or paraxanthine in H2O made the aggregates to dissociate and the heat generated was measured. The reference cell was also filled with distilled H2O. The reference power was set to 4 μcal s−1; initial delay 60 s; stirring speed 400 rpm; and equilibration options were set to fast equilibration; feedback mode high. For both experiments, the initial injection was 5 μL and the rest aliquots were of 15 μL with 300 s time spacing between each injection to ensures the signal returns to the baseline. The filter period was 2 s. The duration of the first injection was 10 s and 30 s for the following ones. The total number of injections was 30. The enthalpy (ΔHdiss) and equilibrium constant (Kdiss) of the dissociation in solutions containing either caffeine or paraxanthine were obtained by integrating each heat peak in the raw calorimetric data (Fig. S7 and S9, ESI†) using a dissociation curve fitting model. The integrated heat plots were acquired (Fig. S8 and S10, ESI†) and the values of ΔHdiss and Kdiss were obtained together with their associated errors. The association constant (Kass), the Gibbs free energy (ΔGdiss) and the entropy (ΔHdiss) changes were calculated according to the equation Kass = 1/Kdiss, ΔGdiss = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kdiss, and ΔGdiss = ΔHdiss − TΔSdiss, where R = 1.987 cal mol−1 K−1 (gas constant) and T = 298 K.
Kdiss, and ΔGdiss = ΔHdiss − TΔSdiss, where R = 1.987 cal mol−1 K−1 (gas constant) and T = 298 K.
Results and discussion
Caffeine dimers
Dimers are the first aggregates that can form during the process of self-association and their structure often corresponds to the building unit of the crystal that grows from solution.63–66 The chemical nature of the intermolecular interactions in the caffeine dimer (CAF)2 can therefore be expected to control its aggregation. The rearrangement of the electronic charge of the face-to-face and face-to-back dimeric configurations found in the X-ray crystalline structure of caffeine67,68 (Fig. S4b and S4b′, ESI†) confirms the presence of six C–H⋯O and C–H⋯N intermolecular hydrogen bonds between the two caffeine molecules.69–72 Although the difference in electronegativity between C and H is small, the weak hydrogen bonds between caffeine molecules play an important role, together with the π–π stacking of the aromatic rings, in controlling the self-association process.73 To evaluate all possible interactions, a computational approach based on probing the potential energy surface of caffeine dimers was applied. Nine low energy configurations for the caffeine dimer (D1–D9) were identified using this approach (Fig. S5, ESI†), five of which had never been reported before.40,69 All these structures present the CH3⋯X (X = N, O) interactions between the two caffeine molecules, therefore confirming their key role. Overall, the gas-phases energy (ΔEe,gas) and Gibbs free energy (ΔGD°) of dimerization were found to be negative. However, in aqueous solution, the formation of dimers D1–D8 is thermodynamically unfavourable (Table 1). The exception is represented by dimer D9 (Fig. 1B), whose liquid-phase reaction is slightly exergonic (ΔGD* = −0.4 kcal mol−1). This therefore suggests that dimer D9 can exist in aqueous solutions. There is much debate on the structural relationship between the most populated dimers in solution and the structural motifs found in solid state forms.53,64,72Fig. 1B and 1C highlight how the structure of the most stable caffeine dimer in water (D9), obtained computationally, correlates very well with the structural synthon found in the X-ray crystal structure (Fig. 1C). On this basis, it can be confirmed that the aggregation of caffeine obeys the so-called “link hypothesis”,72 according to which the transfer of structural information from the liquid- to the solid state-phase is linked to the presence in the solution of stable “face-to-back” dimers.For dimer D9 to have the lowest free energy in solution, Table 1 suggests that it has a contribution of approximately −2 kcal mol−1 from the hydration free energy. This contrasts with dimers D1–D8, whose solvation corrections are all positive, with a range of 1.6 to 4.5 kcal mol−1. Assuming a continuum representation of the solvent, the solvation free energy (ΔGsolv*) is given by two components:57 the electronic polarization term (ΔGEP*), associated with the electrostatic interaction between the solute and the solvent; the free energy change contribution (GCDS*) from solvent cavitation (C), changes in dispersion (D) energy, and possible changes in the local solvent structure (S). For all dimers, the GCDS* contribution to the solvation energy is between 8.7 and 9.2 kcal mol−1. Consequently, the extra-stabilization in the solution of D9 is due to the electronic polarization term. In this configuration, the monomers are almost superimposed (Fig. 1A) and this configuration does not maximize the attractive interaction between electropositive and electronegative parts of the two caffeine molecules. The gas-phase interaction between the two caffeine molecules (ΔEe,gas = −12.87 kcal mol−1) is lower than in dimers D1–D8 (−17 kcal mol−1 < ΔEe,gas < −19 kcal mol−1) and the extra-stabilization is due to the higher electrostatic interaction between D9 and the polarizable solvation model.
The effect of changes to the solvation environment on caffeine dimerization was also investigated by computing the formation of (CAF)2 in three different systems: (i) methanol, a polar protic solvent with a static dielectric constant (ε) lower than water; (ii) acetone, a polar aprotic solvent, and (iii) chloroform, a non polar aprotic solvent. The Boltzmann averaged Gibbs free energy of dimerization obtained for all three systems (Table S5, ESI†) shows an inverse correlation with the dielectric constants.
Caffeine clusters
Given the existing literature data on higher order clusters for caffeine, the next step focused on the stability of these systems.28,35 The configuration of the tetramer was obtained by stacking two dimers of type D9 (the most stable in water) on top of each other. The configuration of the trimer was then obtained by removing one caffeine molecule from the (CAF)4. The optimised structures of the higher order clusters (CAF)3, and (CAF)4 are reported in Fig. 2.Two reaction schemes were used to compute the thermodynamic stability of the trimer in solution: (i) the condensation of D9 with an additional caffeine molecule, (CAF)D9 + CAF → (CAF)3; (ii) the aggregation of three isolated CAF molecules, 3CAF → (CAF)3. For the tetrameter (CAF4), we considered the condensation of two D9 dimers, 2 CAFD9 → (CAF)4, as well as the association of one caffeine molecule to the trimer structure (CAF)3 + CAF → (CAF)4. The energetics of formation of the caffeine trimer and tetramer are listed in Table 2 and show that the free energies of formation of these two species are approximately +2 kcal mol−1. Trimers and tetramers are unstable in water, compared to both the monomer and dimer D9, and unlikely to be present in caffeine aqueous solutions at the concentrations found in biological samples.
Paraxanthine dimers
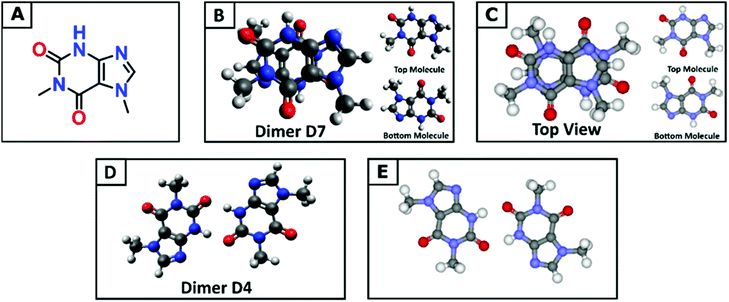
Understanding the molecular structure of the analogues and their self-association behaviour is an important requirement for the evaluation of interactions with biological receptors.74 Paraxanthine (1,7-dimethylxanthine) is the major primary metabolite of caffeine, and although the two molecules are very similar in structure, the removal of one methyl group results in a tenfold decrease in the limit of solubility in water.75 Compared with the nine low energy dimeric configurations of caffeine, the DFT tool identified 20 stable paraxanthine dimers (Fig. S6, ESI†), showing the significant effect of small structural changes in caffeine analogues on the process of self-association. Two types of structures can be identified: (i) dimers D1, D2, D4 and D13, where the two paraxanthine units are linked by two lateral H-bonds; (ii) all remaining (PX)2 structures, where the interaction is controlled by π–π stacking. Dimers D4 and D7 correspond to the synthons in the crystallographic structure of paraxanthine (Fig. 3). The agreement between the simulated building units of paraxanthine in solution and its solid-state structure confirms the efficiency of the computational tool here adopted to identify the possible dimeric structures of caffeine analogues. In the gas phase, most dimers are thermodynamically stable but in aqueous solution, only the configurations forming π–π stacking interactions have a negative free energy of formation (−1.0 ≪ ΔGD* < −0.1 kcal mol−1) (Table S8, ESI†). In water, the Boltzmann averaged value for the dimerization of paraxanthine is −0.11 kcal mol−1. The comparison of the computed thermodynamic stability of the dimers of caffeine and paraxanthine shows that, despite their very small structural difference, the free energy of formation of (PX)2 is 1.1 kcal mol−1 lower than (CAF)2.Experimental ITC verification and solution speciation
ITC experiments were conducted to obtain the enthalpy and equilibrium constant of dissociation of caffeine and paraxanthine in aqueous solution (Table 3). The raw calorimetric data are characterised by positive heat peaks (Fig. S8 and S10, ESI†) indicating that the dissociation for both caffeine and paraxanthine is an endothermic process (ΔHdiss > 0). Fitting of these data to a dimer dissociation model provides constants for both caffeine (Kdiss = 0.112 ± 3.3 × 10−3 M) and paraxanthine (Kdiss = 0.03 ± 1.8 m × 10−3 M). In both cases, the Gibbs free energy of association (ΔGass < 0) is negative. The ΔGass value obtained using ITC measurements (−1.3 kcal mol−1) is in excellent agreement with a previously reported DSC study (ΔGass = −1.5 kcal mol−1 at 25 °C).76 The free energies of dimerization obtained computationally for caffeine (ΔGdim = +0.92 kcal mol−1) and for paraxanthine (ΔGdim = −0.11 kcal mol−1) are approximately 2 kcal mol−1 higher than the experimental values obtained from the ITC experiments (Table 3). However, if the errors associated with the use of the B97-D2/6-31+G(d,p) method together with the SMD/M06-2X/6-31+G(d,p) solvation model [ε(ΔGdim*) =ε(ΔGgas°) +ε(ΔΔGsolv*) = 1.1 kcal mol−1] are taken into account (Section S2, ESI†) there is a good agreement between computational and experimental results. The small values obtained for the free energy of dimerization of both caffeine and paraxanthine (<2 kcal mol−1) also confirm that the monomer and dimer can coexist in solution. The results from the computational approach are considerably closer to the experimental values, and represent a significant improvement compared to previously published data, which reported free energies of dimerization (+12 kcal mol−1) considerably higher.40,41 Furthermore, the difference in the Gibbs free energy of association between caffeine and paraxanthine (ΔΔGass = ΔGCAFass − ΔGPXass) obtained by ITC (0.6 kcal mol−1) and DFT (1.1 kcal mol−1) is also in excellent accordance, providing strong evidence for the use of our computational approach to predict the self-association behaviour in solution of adenosine-analogues.| Molecule | ΔHass (ITC) | ΔGass (ITC) | ΔGD* (DFT) |
|---|---|---|---|
| Caffeine | −5.25 ± 0.04 | −1.30 ± 0.71 | +0.92 ± 1.10 |
| Paraxanthine | −2.83 ± 0.07 | −1.89 ± 0.35 | −0.11 ± 1.10 |
Having demonstrated that at low concentrations both caffeine and paraxanthine are potentially present in solution only as a combination of monomers and dimers, the experimental and computational values of ΔGass were used in the monomer–dimer model to estimate the percentage of dimer in solution as a function of total concentration:77
 | (6) |
Fig. 4 shows the computational and experimental profiles of the dimer percentage in solution for caffeine and paraxanthine in the 5–50 μM concentration range, which is close to the one found in biological samples. The computational data consistently suggest a lower percentage of the dimer in solution compared to ITC for both paraxanthine and caffeine. This is due to the value of ΔGD* obtained from DFT calculations, for both molecules, being about 2 kcal mol−1 more positive than ΔGass obtained from ITC measurements. For both approaches, computational and ITC, paraxanthine is found to be present as a dimer in higher concentrations compared to caffeine, which may be related to the differences in solubility of the two molecules (PX = 5 mM, CAF 82 mM). This behaviour is observed not only at very low concentrations, but also towards the limit of solubility (Fig. S11, ESI†). The results therefore indicate that both paraxanthine and caffeine, when evaluated at the concentrations found in biological samples (10 μM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 36), are predominantly present as monomers, with less than 0.05% dimer in solution.
36), are predominantly present as monomers, with less than 0.05% dimer in solution.
Conclusions
We presented a DFT-based computational tool that allowed the study of the self-assembly behaviour in solution of two adenosine-analogues like caffeine and paraxanthine, and we demonstrated that for both molecules, the formation of higher order clusters is thermodynamically disfavoured. The results were validated experimentally by ITC measurements, which provided values for the Gibbs free energy of association consistent with the DFT results. Significantly, we showed how the computational approach allows prediction of the effect of small structural changes on the chemical structure and thermodynamic stability of clusters resulting from self-assembly. In low concentration solutions, both caffeine and paraxanthine are mainly present as monomers, with less than 0.05% dimer present in 10 μM solutions. The computational method used here is a valid tool to quantify the speciation of adenosine-analogues and predict accurately their behaviour in solution, which can provide a standardised and faster approach to the evaluation of potential new drug leads.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 642014 (IPCOS). The authors would like to acknowledge Dr L. Navarini for helpful discussions. This research utilized Queen Mary's Apocrita HPC facility, supported by QMUL Research-IT. Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by the EPSRC (EP/L000202, EP/R029431), this work used the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk).References
- G. Haskó, J. Linden, B. Cronstein and P. Pacher, Adenosine receptors: therapeutic aspects for inflammatory and immune diseases, Nat. Rev. Drug Discovery, 2008, 7, 759 CrossRef PubMed.
- E. S. Hayes, Adenosine receptors and cardiovascular disease, Cardiovasc. Toxicol., 2003, 3, 71–88 CrossRef CAS PubMed.
- T. W. Stone, S. Ceruti and M. P. Abbracchio, in Adenosine Receptors in Health and Disease, ed. C. N. Wilson and S. J. Mustafa, Springer, Berlin, Heidelberg, 2009, pp. 535–587 Search PubMed.
- C. Cekic, D. Sag, Y. Li, D. Theodorescu, R. M. Strieter and J. Linden, Adenosine A2B Receptor Blockade Slows Growth of Bladder and Breast Tumors, J. Immunol., 2012, 188, 198–205 CrossRef CAS PubMed.
- P. Fishman, S. Baryehuda, L. Madi, I. Cohn, P. Tikva, I. C. Biopharma and P. Tikva, A3 adenosine receptor as a target for cancer therapy, Anticancer Drugs, 2002, 13, 437–443 CrossRef CAS PubMed.
- A. K. Dhalla, J. C. Shryock, R. Shreeniwas and L. Belardinelli, Curr. Top. Med. Chem., 2003, 3, 369–385 CrossRef CAS PubMed.
- S. Crunkhorn, Antiviral drugs: Adenosine analogue blocks dengue infection, Nat. Rev. Drug Discovery, 2010, 9, 21 CrossRef CAS.
- K. R. Jones, U. Choi, J. L. Gao, R. D. Thompson, L. E. Rodman, H. L. Malech and E. M. Kang, A novel method for screening adenosine receptor specific agonists for use in adenosine drug development, Sci. Rep., 2017, 7, 1–10 CrossRef PubMed.
- S. Hall, B. Desbrow, S. Anoopkumar-Dukie, A. K. Davey, D. Arora, C. McDermott, M. M. Schubert, A. V. Perkins, M. J. Kiefel and G. D. Grant, A review of the bioactivity of coffee, caffeine and key coffee constituents on inflammatory responses linked to depression, Food Res. Int., 2015, 76, 626–636 CrossRef CAS PubMed.
- I. A. Ludwig, M. N. Clifford, M. E. J. Lean, H. Ashihara and A. Crozier, Coffee: biochemistry and potential impact on health, Food Funct., 2014, 5, 1695–1717 RSC.
- J. V. Higdon and B. Frei, Coffee and health: A review of recent human research, Crit. Rev. Food Sci. Nutr., 2006, 46, 101–123 CrossRef CAS PubMed.
- S. Ruiz-Crespo, J. M. Trejo-Gabriel-Galan, M. Cavia-Saiz and P. Muñiz, Coffee component 3-caffeoylquinic acid increases antioxidant capacity but not polyphenol content in experimental cerebral infarction, Neurochem. Res., 2012, 37, 1085–1090 CrossRef CAS PubMed.
- M. S. Caubet, W. Elbast, M. C. Dubuc and J. L. Brazier, Analysis of urinary caffeine metabolites by HPLC-DAD: The use of metabolic ratios to assess CYP1A2 enzyme activity, J. Pharm. Biomed. Anal., 2002, 27, 261–270 CrossRef CAS PubMed.
- M. S. Caubet, B. Comte and J. L. Brazier, Determination of urinary13C-caffeine metabolites by liquid chromatography-mass spectrometry: The use of metabolic ratios to assess CYP1A2 activity, J. Pharm. Biomed. Anal., 2004, 34, 379–389 CrossRef CAS PubMed.
- V. Perera, A. S. Gross, H. Xu and A. J. McLachlan, Pharmacokinetics of caffeine in plasma and saliva, and the influence of caffeine abstinence on CYP1A2 metrics, J. Pharm. Pharmacol., 2011, 63, 1161–1168 CrossRef CAS PubMed.
- N. Y. Jordan, J. Y. Mimpen, W. J. M. van den Bogaard, F. M. Flesch, M. H. M. van de Meent and J. S. Torano, Analysis of caffeine and paraxanthine in human saliva with ultra-high-performance liquid chromatography for CYP1A2 phenotyping, J. Chromatogr. B: Anal. Technol. Biomed. Life Sci., 2015, 995–996, 70–73 CrossRef CAS PubMed.
- M. A. Heckman, J. Weil and E. G. De Mejia, Caffeine (1,3,7-trimethylxanthine) in Food: A Comprehensive Review on Consumption, Functionality, Safety, and Regulatory Matters, J. Food Sci., 2010, 75, R77–R87 CrossRef CAS PubMed.
- B. B. Fredholm, K. Bättig, J. Holmén, A. Nehlig and E. E. Zvartau, Actions of caffeine in the brain with special reference to factors that contribute to its widespread use, Pharmacol. Rev., 1999, 51, 83–133 CAS.
- A. Nehlig, Is caffeine a cognitive enhancer?, J. Alzheimer's Dis., 2010, 20, S85–S94 CAS.
- V. L. Batalha, D. G. Ferreira, J. E. Coelho, J. S. Valadas, R. Gomes, M. Temido-Ferreira, T. Shmidt, Y. Baqi, L. Buée, C. E. Müller, M. Hamdane, T. F. Outeiro, M. Bader, S. H. Meijsing, G. Sadri-Vakili, D. Blum and L. V. Lopes, The caffeine-binding adenosine A 2A receptor induces age-like HPA-axis dysfunction by targeting glucocorticoid receptor function, Sci. Rep., 2016, 6, 31493 CrossRef CAS PubMed.
- L. F. Zhang, Z. W. Zhou, Z. H. Wang, Y. H. Du, Z. X. He, C. Cao and S. F. Zhou, Coffee and caffeine potentiate the antiamyloidogenic activity of melatonin via inhibition of aβ oligomerization and modulation of the Tau-mediated pathway in N2a/APPcells, Drug Des., Dev. Ther., 2015, 9, 241–272 CAS.
- D. Borota, E. Murray, G. Keceli, A. Chang, J. M. Watabe, M. Ly, J. P. Toscano and M. A. Yassa, Post-study caffeine administration enhances memory consolidation in humans, Nat. Neurosci., 2014, 17, 201–203 CrossRef CAS PubMed.
- I. Horman and B. Dreux, Dimerisation of caffeine, Helv. Chim. Acta, 1985, 68, 72–75 CrossRef CAS.
- D. B. Davies, D. A. Veselkov, L. N. Djimant and A. N. Veselkov, Hetero-association of caffeine and aromatic drugs and their competitive binding with a DNA oligomer, Eur. Biophys. J., 2001, 30, 354–366 CrossRef CAS PubMed.
- N. D’Amelio, L. Fontanive, F. Uggeri, F. Suggi-Liverani and L. Navarini, NMR reinvestigation of the caffeine-chlorogenate complex in aqueous solution and in coffee brews, Food Biophys., 2009, 4, 321–330 CrossRef.
- M. Falk, M. Gil and N. Iza, Self-association of caffeine in aqueous solution: an FT-IR study, Can. J. Chem., 1990, 68, 1293–1299 CrossRef CAS.
- S. Banerjee, D. Bhowmik, P. K. Verma, R. K. Mitra, A. Sidhhanta, G. Basu and S. K. Pal, Ultrafast spectroscopic study on caffeine mediated dissociation of mutagenic ethidium from synthetic DNA and various cell nuclei, J. Phys. Chem. B, 2011, 115, 14776–14783 CrossRef CAS PubMed.
- L. Tavagnacco, Y. Gerelli, A. Cesàro and J. W. Brady, Stacking and Branching in Self-Aggregation of Caffeine in Aqueous Solution: From the Supramolecular to Atomic Scale Clustering, J. Phys. Chem. B, 2016, 120, 9987–9996 CrossRef CAS PubMed.
- E. L. Farquhar, M. Downing and S. J. Gill, The Enthalpy of Self-Association of Pyrimidine Derivatives in Water, Biochemistry, 1968, 7, 1224–1225 CrossRef CAS PubMed.
- S. Banerjee, P. K. Verma, R. K. Mitra, G. Basu and S. K. Pal, Probing the interior of self-assembled caffeine dimer at various temperatures, J. Fluoresc., 2012, 22, 753–769 CrossRef CAS PubMed.
- H. Bothe and H. K. Cammenga, Calorimetric Investigation of Aqueous Caffeine Solution and Molecular Association of Caffeine, Thermochim. Acta, 1983, 69, 235–252 CrossRef CAS.
- A. Cesàro and G. Starec, Thermodynamic properties of caffeine crystal forms, J. Phys. Chem., 1980, 84, 1345–1346 CrossRef.
- L. Tavagnacco, S. Di Fonzo, F. D’Amico, C. Masciovecchio, J. Brady and A. Cesàro, Stacking of purines in water: the role of dipolar interaction in caffeine, Phys. Chem. Chem. Phys., 2016, 13478–13486 RSC.
- L. Tavagnacco, O. Engström, U. Schnupf, M. L. Saboungi, M. Himmel, G. Widmalm, A. Cesàro and J. W. Brady, Caffeine and sugars interact in aqueous solutions: A simulation and NMR study, J. Phys. Chem. B, 2012, 116, 11701–11711 CrossRef CAS PubMed.
- L. Tavagnacco, P. E. Mason, G. W. Neilson, M. L. Saboungi, A. Cesàro and J. W. Brady, Molecular Dynamics and Neutron Scattering Studies of Mixed Solutions of Caffeine and Pyridine in Water, J. Phys. Chem. B, 2018, 122, 5308–5315 CrossRef CAS PubMed.
- E. Schievano, C. Finotello, L. Navarini and S. Mammi, Quantification of caffeine in human saliva by nuclear magnetic resonance as an alternative method for cytochrome CYP1A2 phenotyping, Talanta, 2015, 140, 36–41 CrossRef CAS PubMed.
- V. Perera, A. S. Gross and A. J. McLachlan, Caffeine and paraxanthine HPLC assay for CYP1A2 phenotype assessment using saliva and plasma, Biomed. Chromatogr., 2010, 24, 1136–1144 CrossRef CAS PubMed.
- F. Chen, Z.-Y. Hu, R. B. Parker and S. C. Laizure, Measurement of caffeine and its three primary metabolites in human plasma by HPLC-ESI-MS/MS and clinical application, Biomed. Chromatogr., 2017, 1, 115–141 Search PubMed.
- R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, The solvation, partitioning, hydrogen bonding, and dimerization of nucleotide bases: a multifaceted challenge for quantum chemistry, Phys. Chem. Chem. Phys., 2011, 13, 10908–10922 RSC.
- R. Senthilnithy, M. S. S. Weerasingha and D. P. Dissanayake, Interaction of caffeine dimers with water molecules, Comput. Theor. Chem., 2014, 1028, 60–64 CrossRef CAS.
- E. S. Bradley and C. H. Hendon, The impact of solvent relative permittivity on the dimerisation of organic molecules well below their solubility limits: examples from brewed coffee and beyond, Food Funct., 2017, 8, 1037–1042 RSC.
- E. G. Hohenstein, S. T. Chill and C. D. Sherrill, Assessment of the Performance of the M05-2X and M06-2X Exchange-Correlation Functionals for Noncovalent Interactions in Biomolecules, J. Chem. Theory Comput., 2008, 4, 1996–2000 CrossRef CAS PubMed.
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, NWChem: A comprehensive and scalable open-source solution for large scale molecular simulations, Comput. Phys. Commun., 2010, 181, 1477–1489 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford, 2009 Search PubMed.
- S. Grimme, Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- R. Ditchfield, W. J. Hehre and J. A. Pople, Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- K. E. Riley, M. Pitoňák, J. Černý and P. Hobza, On the Structure and Geometry of Biomolecular Binding Motifs (Hydrogen-Bonding, Stacking, X−H⋯π): WFT and DFT Calculations, J. Chem. Theory Comput., 2010, 6, 66–80 CrossRef CAS PubMed.
- R. Podeszwa, K. Patkowski and K. Szalewicz, Improved interaction energy benchmarks for dimers of biological relevance, Phys. Chem. Chem. Phys., 2010, 12, 5974–5979 RSC.
- K. E. Riley, M. Pitončák, P. Jurecčka and P. Hobza, Stabilization and structure calculations for noncovalent interactions in extended molecular systems based on wave function and density functional theories, Chem. Rev., 2010, 110, 5023–5063 CrossRef CAS PubMed.
- J. Klimeš and A. Michaelides, Perspective: Advances and challenges in treating van der Waals dispersion forces in density functional theory, J. Chem. Phys., 2012, 137, 1–15 CrossRef PubMed.
- B. J. Lynch, Y. Zhao and D. G. Truhlar, Effectiveness of Diffuse Basis Functions for Calculating Relative Energies by Density Functional Theory, J. Phys. Chem. A, 2003, 107, 1384–1388 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other function, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- D. Di Tommaso, The molecular self-association of carboxylic acids in solution: testing the validity of the link hypothesis using a quantum mechanical continuum solvation approach, CrystEngComm, 2013, 15, 6564–6577 RSC.
- D. Di Tommaso and K. L. Watson, Density functional theory study of the oligomerization of carboxylic acids, J. Phys. Chem. A, 2014, 118, 11098–11113 CrossRef CAS PubMed.
- S. F. Boys and F. Bernardi, The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- J. Deng, A. T. B. Gilbert and P. M. W. Gill, Communication: Efficient counterpoise corrections by a perturbative approach, J. Chem. Phys., 2011, 135, 81105 CrossRef PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on the Generalized Born Approximation with Asymmetric Descreening, J. Chem. Theory Comput., 2009, 5, 2447–2464 CrossRef CAS PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. Ho, A. Klamt and M. L. Coote, Comment on the Correct Use of Continuum Solvent Models, J. Phys. Chem. A, 2010, 114, 13442–13444 CrossRef CAS PubMed.
- E. Gaines and D. Di Tommaso, Solvation and Aggregation of Meta-Aminobenzoic Acid in Water: Density Functional Theory and Molecular Dynamics Study, Pharmaceutics, 2018, 10, 12 CrossRef PubMed.
- L. A. Montero, A. M. Esteva, J. Molina, A. Zapardiel, L. Herna, H. Màrquez and A. Acosta, A Theoretical Approach to Analytical Properties of 2,4-Diamino-5-phenylthiazole in Water Solution. Tautomerism and Dependence on pH, J. Am. Chem. Soc., 1998, 120, 12023–12033 CrossRef CAS.
- S. Parveen, R. J. Davey, G. Dent and R. G. Pritchard, Linking solution chemistry to crystal nucleation: the case of tetrolic acid, Chem. Commun., 2005, 1531–1533 RSC.
- R. J. Davey, S. L. M. Schroeder and J. H. Ter Horst, Nucleation of organic crystals - A molecular perspective, Angew. Chem., Int. Ed., 2013, 52, 2167–2179 CrossRef PubMed.
- E. Gaines, K. Maisuria and D. Di Tommaso, The role of solvent in the self-assembly of m-aminobenzoic acid: a density functional theory and molecular dynamics study, CrystEngComm, 2016, 18, 2937–2948 RSC.
- A. J. Cruz-Cabeza, R. J. Davey, S. S. Sachithananthan, R. Smith, S. K. Tang, T. Vetter and Y. Xiao, Aromatic stacking – a key step in nucleation, Chem. Commun., 2017, 53, 7905–7908 RSC.
- C. W. Lehmann and F. Stowasser, The crystal structure of anhydrous beta-caffeine as determined from X-ray powder-diffraction data, Chem. – Eur. J., 2007, 13, 2908–2911 CrossRef CAS PubMed.
- J. D. Sutor, The Structure of the Pyrimidines and Purines. VII. The Crystal Structure of Caffeine, Acta Crystallogr., 1965, 19, 453–458 Search PubMed.
- V. I. Poltev, T. I. Grokhlina, E. González, A. Deriabina, A. Cruz, L. Gorb, J. Leszczynski, L. N. Djimant and A. N. Veselkov, The study of three-dimensional structure of caffeine associates using computational and experimental methods, J. Mol. Struct. THEOCHEM, 2004, 709, 123–128 CrossRef CAS.
- M. Karthika, L. Senthilkumar and R. Kanakaraju, Theoretical studies on hydrogen bonding in caffeine-theophylline complexes, Comput. Theor. Chem., 2012, 979, 54–63 CrossRef CAS.
- J. D. Sutor, Evidence of the existence of C–H⋯O Hydrogen Bonds in Crystals, J. Chem. Soc., 1963, 1105–1110 RSC.
- R. J. Davey, G. Dent, R. K. Mughal and S. Parveen, Concerning the Relationship between Structural and Growth Synthons in Crystal Nucleation: Solution and Crystal Chemistry of Carboxylic Acids As Revealed through IR Spectroscopy, Cryst. Growth Des., 2006, 6, 1788–1796 CrossRef CAS.
- E. A. Meyer, R. K. Castellano and F. Diederich, Interactions with Aromatic Rings in Chemical and Biological Recognition, Angew. Chem., Int. Ed., 2003, 42, 1210–1250 CrossRef CAS PubMed.
- M. B. Patrascu, E. Malek-Adamian, M. J. Damha and N. Moitessier, Accurately modeling the conformational preferences of nucleosides, J. Am. Chem. Soc., 2017, 139, 13620–13623 CrossRef PubMed.
- S. C. B. Inc, Paraxanthine technical Information.
- S. J. Gill, M. Downing and G. F. Sheats, The Enthalpy of Self-Association of Purine Derivates in Water, Biochemistry, 1967, 6, 272–276 CrossRef CAS PubMed.
- T. Krishnan, W. C. Duer, S. Goldman and J.-L. Fortier, On the use of dilution calorimetry in the study of hydrogen-bonding self-association reactions: benzoic acid in benzene, Can. J. Chem., 1979, 57, 530–537 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp05647a |
| ‡ These authors contributed equally to this work. |
| This journal is © the Owner Societies 2019 |