Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Doping engineering of thermoelectric transport in BNC heteronanotubes†
Leonardo
Medrano Sandonas
 *abc,
Gustavo
Cuba-Supanta
d,
Rafael
Gutierrez
a,
Carlos V.
Landauro
de,
Justo
Rojas-Tapia
*abc,
Gustavo
Cuba-Supanta
d,
Rafael
Gutierrez
a,
Carlos V.
Landauro
de,
Justo
Rojas-Tapia
 d and
Gianaurelio
Cuniberti
acf
d and
Gianaurelio
Cuniberti
acf
aInstitute for Materials Science and Max Bergmann Center of Biomaterials, TU Dresden, 01062 Dresden, Germany. E-mail: leonardo.medrano@nano.tu-dresden.de; Fax: +49 351 4633 1422; Tel: +49 351 4633 1419
bMax Planck Institute for the Physics of Complex Systems, 01187 Dresden, Germany
cCenter for Advancing Electronics Dresden, TU Dresden, 01062 Dresden, Germany
dFaculty of Physical Sciences, National University of San Marcos, P.O. Box 14-0149, Lima 14, Peru
eCentro de Investigaciones Tecnológicas, Biomédicas y Medioambientales (CIBTM), Bella Vista, Callao, Peru
fDresden Center for Computational Materials Science (DCMS), TU Dresden, 01062 Dresden, Germany
First published on 17th December 2018
Abstract
BNC heteronanotubes are promising materials for the design of nanoscale thermoelectric devices. In particular, the structural BN doping pattern can be exploited to control the electrical and thermal transport properties of BNC nanostructures. We here address the thermoelectric transport properties of (6,6)-BNC heteronanotubes with helical and horizontal BN doping patterns. For this, we use a density functional tight-binding method combined with the Green's function technique. Our results show that the electron transmission is reduced and the electronic bandgap increased as a function of the BN concentration for different doping distribution patterns, so that (6,6)-BNC heteronanotubes become semiconducting with a tunable bandgap. The thermal conductance of helical (6,6)-BNC heteronanotubes, which is dominated by phonons, is weakly dependent on BN concentration in the range of 30–80%. Also, the Seebeck coefficient is enhanced by increasing the concentration of helical BN strips. In particular, helical (6,6)-BNC heteronanotubes with a high BN concentration (>20%) display a larger figure of merit compared to other doping distributions and, for a concentration of 50%, reach values up to 2.3 times and 3.4 times the corresponding values of a CNT at 300 K and 800 K, respectively. Our study yields new insights into the parameters tuning the thermoelectric efficiency and thus provides a starting point for designing thermoelectric devices based on BNC nanostructures.
1 Introduction
Since their discovery in 1991 by Iijima, carbon nanotubes (CNTs) have become one of the most intensively studied low dimensional systems.1–4 Their fascinating physical and chemical properties have made them ideal candidates for a broad spectrum of applications in nanoelectronics, energy harvesting, and optoelectronics.5,6 In particular, single-walled carbon nanotubes including substitutional impurities have been used as diodes and field-effect transistors due to the possibility of tuning their electrical response via controlled doping with other atomic species.7,8 Ternary boron carbonitride nanotubes belong to this class and have recently been the focus of theoretical and experimental activities because of their excellent mechanical, electrical and non-linear optical properties.9–11 One of the major effects revealed in these studies is the possibility of significantly modifying the electronic bandgap over a wide range by varying the chemical composition rather than by geometrical modifications.12–16 Despite many difficulties involved in their preparation, boron carbonitride heteronanotubes have been successfully synthesized using methods such as arc-discharge,17 laser vaporization,18 chemical vapor deposition,19,20 electron beam irradiation,21 and pyrolysis techniques.22,23 Hence, the prospect of designing hybrid nanotubes combining BN and C is of particular interest, since it provides a reliable and economical way to achieve rectifying diodes, molecular sensors, transistors, and high-efficiency solar cells.20,24,25In particular, BNC heteronanotubes are expected to play an important role as a new generation of thermoelectric materials, and they are also of great interest in environmentally relevant issues such as waste heat recovery and solid-state cooling.26,27 The efficiency of a thermoelectric material is measured by its figure of merit, ZT = S2GT/(κel + κph), where G is the electrical conductance, S is the Seebeck coefficient, T is the absolute temperature, and κel(ph) is the electronic (phononic) thermal conductance. The larger the ZT, the better the thermoelectric performance of a material. Thus, promising thermoelectric materials should simultaneously have a high power factor (defined as the product GS2) and low thermal conductance, ideally implementing an electron crystal and a phonon glass. Hence, in order to make thermoelectric materials more competitive than conventional refrigerators and generators, routes for tuning both transport quantities, electrical and thermal, need to be developed.
So far, the experimental studies of the doping influence on the thermoelectric properties of CNTs have been focused on molecular dopants.28 Early studies have been carried out on the influence of only nitrogen and only boron doping but without clear conclusions about how they may affect the figure of merit of CNTs.29 On the other hand, the thermoelectric properties of hybrid graphene/boron-nitride nanoribbons have been studied over the last few years using various theoretical tools. Thus, using a non-equilibrium Green's function (NEGF) approach, Yang et al.30 have shown that, in comparison to pristine graphene ribbons, the figure of merit for armchair BNC nanoribbons is enhanced by 10–20 times, while for zigzag nanoribbons, ZT could be increased by a factor of 2–3. Molecular dynamics simulations were used to study thermal transport in planar BNC heterostructures, finding that the BC2N monolayer displays a strong anisotropy of in-plane thermal transport31 and the thermal conduction in free-standing asymetric BNC nanoribbons is improved after substrate deposition.32 It has also been experimentally observed that the thermal conductivity of BNC heteronanotubes increases with increasing temperature up to room temperature, with no sign of saturation.33 Moreover, the electron transport properties of BNC heteronanotubes have been widely investigated using a method combining density functional theory with NEGF.34–37 Heteronanotubes were found to have a tunable electronic bandgap and to exhibit negative differential resistance and rectifying behavior. All these novel effects in BNC heteronanotubes strongly depend on their structure and configuration, which can be controlled with the concentration of BN and C domains.15,38,39
The main goal of the present work is to investigate (i) the influence of BN and C domain distributions on the thermoelectric transport properties of (6,6)-BNC heteronanotubes, and (ii) the influence of varying concentration. We use a Density Functional Tight-Binding (DFTB) method combined with NEGF, which offers a powerful technique to deal with quantum electron and phonon transport properties of large nanoscale systems and, hence, to compute their thermoelectric properties.40–42 Here, we will study only one type of carbon nanotube and focus on the effect of doping engineering on the transport properties. However, we may expect that nanotubes with similar physical properties will display the same trends. In particular, we will focus on a helical spatial distribution of substitutional impurities, which has recently been proved to be a crucial factor in designing a novel nano-inductor,36 and which also induces a non-monotonous dependence of the electronic bandgap on the helical pattern.37 Our work demonstrates that helical BN strips considerably enhance the thermoelectric transport properties of (6,6)-CNT, improving the Seebeck coefficient and obtaining ZT up to 3.4 times its initial value. Moreover, these values are larger than those corresponding to structures with either a random distribution of BN atoms or with horizontal (i.e. parallel to the nanotube axis) BN stripes.
2 Computational method
2.1 Nanotube models
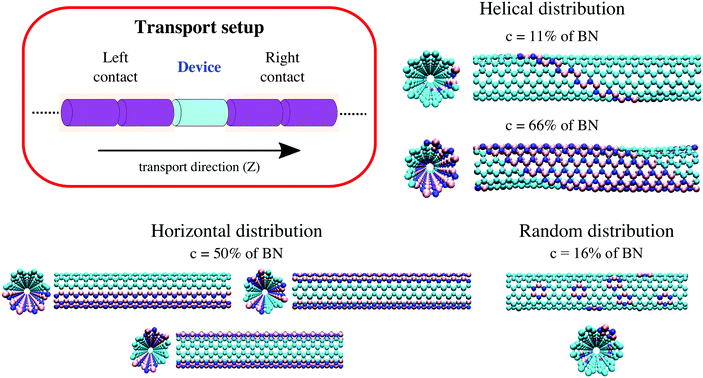
We will consider in this study three different BN doping distribution patterns of a carbon nanotube: helical, horizontal, and random. For this, we consider a (6,6)-CNT of length 43.3 Å and radius 4.07 Å as a reference structure in a supercell composed by 432 C atoms. Helical BN strips, BN chains (parallel to the transport direction, which corresponds to the Z-axis), and BN rings (one ring containing 3B and 3N atoms) have then been introduced in an otherwise perfect (6,6)-CNT to represent helical, horizontal, and random impurity distributions, as shown in Fig. 1. For the helical distribution, the BN concentration is varied from c = 11% to c = 89% following a helix angle of 60°. For the other cases, we have considered concentrations ranging from c = 16% to c = 84%. The limits of 0% and 100% correspond to carbon and boron nitride nanotubes, respectively.Before performing the transport calculations, all (6,6)-BNC heteronanotube geometries (supercells) have first been optimized by using a DFTB method as implemented in the DFTB+ software package.43,44 This method combines accuracy with numerical efficiency, and it allows dealing with systems up to 2000 atoms in a quantum simulation.40,42,45,46 Optimizations were performed until the absolute value of the inter-atomic forces was below 10−6 atomic units with a k-point mesh of 1 × 1 × 8 (optimal mesh). Periodic boundary conditions were imposed along the Z-axis. The values of C–C and B–N bond lengths are 1.43 Å and 1.48 Å, respectively. After optimization, the helical BNC heteronanotubes display a smooth wave-like profile along the axial direction (mainly around the C stripes). This is related to the difference between bond lengths at the interfaces: C–B ∼ 1.49 Å and C–N ∼ 1.36 Å, see e.g.ref. 37 and 38. The horizontally doped nanotubes have weakly elongated cross sections with a BN concentration dependent eccentricity (see Fig. 1), confirming the results reported by Guedes et al.39
2.2 Transport calculation method
Neglecting electron–phonon and phonon–phonon interactions, which would need a separate study, both electronic and phonon transport channels can be considered as independent from each other. Then, the (ballistic) electron and phonon transport properties can be computed within the Landauer approach in terms of the corresponding electronic τel(E) and phononic τph(ω) transmission coefficients. Using non-equilibrium thermodynamics and series expansions of the electrical current in the low bias, linear response regime, closed expressions for the different electronic transport coefficients appearing in the definition of the figure of merit can be written as:40,41,47| G = e2L0, | (1) |
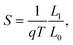 | (2) |
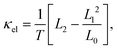 | (3) |
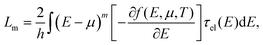 | (4) |
For phonon transport, the corresponding linear thermal conductance is given by:
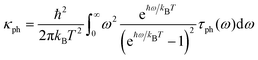 | (5) |
| τel(E) = Trace(GrΓLGaΓR), | (6) |
We use a common partitioning scheme for both electrons and phonons by dividing the system into three regions, namely left contact, right contact, and a central (or device) region (see Fig. 1). For all doping distributions, the contacts are considered semi-infinite and composed by twice the previously optimized supercell (see Section 2.1), while the central region includes only one supercell. Consequently, there are no effects related to interface scattering between the contacts and the central region, neither for electrons nor phonons, and the whole system can be treated as an infinite system without the need of imposing periodic boundary conditions. For the helical distribution, we have however studied an extra case by considering metal electrodes purely made of (6,6)-CNTs and the central region including a finite helical (6,6)-BNC heteronanotube, producing scattering at the contact–device interface (see Fig. S9 in the ESI†).
3 Results and discussion
3.1 Electron and phonon transport
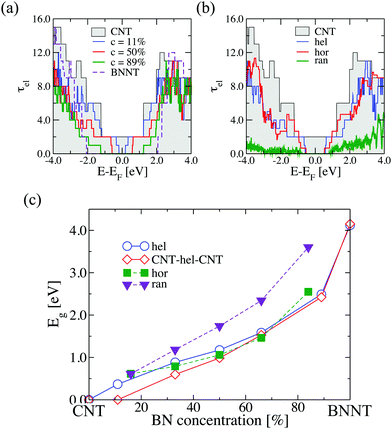
We first analyze the electronic transport properties of helical (6,6)-BNC heteronanotubes. In Fig. 2(a), we show the influence of helical BN stripes on the electron transmission function of a (6,6)-CNT, which displays metallic behavior as a pristine material.12 The width of the B–N stripes is given by WBN; the corresponding widths for a concentration of c = 11% and c = 89% are WBN = 2.46 Å and WBN = 27.06 Å, respectively. The addition of B and N substitutional impurities mostly suppresses the electron transport channels around the Fermi energy, EF, and the nanotube becomes semiconducting with a tunable electronic bandgap, Eg. This is mainly due to the removal of the p-like electronic states from C atoms, which are dominant in that energy range (see Fig. S1 in the ESI†). For a full coverage of C sites, a pristine (6,6)-BN nanotube is obtained as a limiting case with a bandgap of ∼4.1 eV, which could make this nanotube inappropriate for technological applications. The suppression of transport channels also occurs when other spatial doping distributions are considered, however, the influence on the magnitude of the transmission is different for each case, as illustrated in Fig. 2(b) for a fixed BN concentration of 50%. As expected, a fully random distribution of atoms strongly reduces the transmission over all electron energies. This is clearly a result of Anderson-type localization of the electronic states. The (6,6)-BNC heteronanotubes with helical and horizontal stripes show qualitatively similar transmission functions, with the horizontal stripe arrangement showing a tendency of a larger transmission within an energy window of ±2 eV around the Fermi energy. The weaker suppression of the transmission function of the helical and horizontal stripes compared to the purely disordered nanotube is related to the long-range spatial correlations resulting from the symmetry of the BN atomic arrangements along the pristine nanotube.In Fig. 2(c), we show as a summary the influence of varying BN concentration on the bandgap for the three spatial disorder distributions: random, helical stripes, and horizontal stripes. The latter two display very similar quantitative trends in Eg. A similar behavior of the electronic bandgap in horizontal BNC heteronanotubes has been reported by Guedes et al.39 For nanotubes with randomly distributed BN domains, the low-energy transport channels are largely suppressed leading to a larger bandgap, which increases with increasing BN concentration. In Fig. 2(c) we also show, for comparison, the behavior of the band gap in the case of a finite size helical (6,6)-BNC heteronanotube connected to pure CNT electrodes. Interestingly, the system retains the metallic character of the pristine (6,6)-CNT at concentrations below c = 10%, while with increasing concentration, a gap opens and the quantitative trend becomes very similar to the case of the full helical distribution.
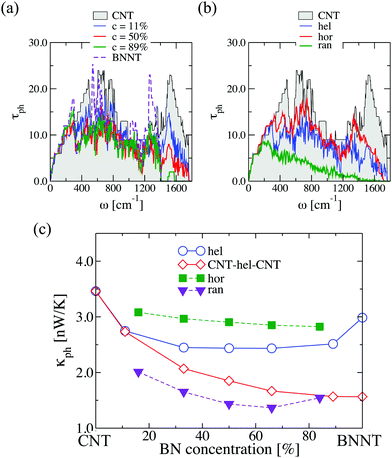
The importance of controlling the doping distribution pattern is also seen in the phonon transport properties, as shown in Fig. 3. The effect of increasing concentration for a given BN helical distribution is mostly seen in a dramatic suppression of high frequency vibrational modes (ω > 1400 cm−1), which correspond to relatively local vibrations involving carbon atoms (see Fig. S5 in the ESI†). The transmission of low-frequency (long wavelength) vibrations below 200 cm−1 is, on the contrary, barely changed when varying the disorder concentration (the width of the helical stripes). Similar to the electronic case, we plot in Fig. 3(b) the phonon transmission functions of (6,6)-BNC heteronanotubes with fixed concentration c = 50% and different BN spatial arrangements. Overall, the phonon transmission is strongly suppressed for all BN spatial distributions when compared with the pristine CNT reference system, with the exception of the long wavelength modes. As expected, a purely random distribution of B and N atoms largely blocks the transmission over almost the whole frequency spectrum; only the low-frequency modes experience less scattering at the localized impurities (BN rings) and therefore their transmission is much less affected. Regarding the more structurally ordered helical and horizontal arrangements, we see that the former leads to a stronger reduction of the transmission in the high-frequency domain (ω > 1400 cm−1) of the spectrum due to the absence of B–N–C local vibrations. Most high-frequency vibrations in helical (6,6)-BNC heteronanotubes correspond to carbon atoms only (see Fig. S6 in the ESI†).
The corresponding phonon thermal conductance, κph, at T = 300 K is displayed in Fig. 3(c). We have plotted the variation of κph as a function of the BN concentration for each doping distribution pattern. (6,6)-CNT displays a thermal conductance of 3.46 nW K−1, which is close to the experimental value estimated by E. Pop et al. (2.4 nW K−1) for CNTs of a length of ∼2.6 μm and a diameter of 1.7 nm.50 We also found that the thermal conductance of semi-infinite helical (6,6)-BNC heteronanotubes remains nearly constant (∼2.5 nW K−1) for concentrations between 30% and 80%, and then increases until it reaches the value corresponding to a pristine BNNT, κph ∼ 3.0 nW K−1. Moreover, as is expected from the behavior of the phonon transmission function, horizontal BNC heteronanotubes show the highest thermal conductance while the lowest κph values were obtained for (6,6)-CNT with BN domains randomly distributed. Connecting the helical (6,6)-BNC heteronanotube to (6,6)-CNT electrodes leads to a continuous suppression of the thermal conductance with increasing concentration. We remark that for the temperature used in this calculation (T = 300 K), the dominant contribution to the thermal conductance mostly originates from long wavelength modes with frequencies ≤200 cm−1. Hence, we expect that the influence of the BN concentration on the electron and phonon transport properties (namely, opening of the electronic band gap and reduction of the thermal conductance) of conducting nanotubes will be qualitatively similar for other types of metallic nanotubes, although quantitative differences may obviously exist concerning, e.g., the minimal amount of doping required to open a gap, etc.
3.2 Thermoelectric transport properties
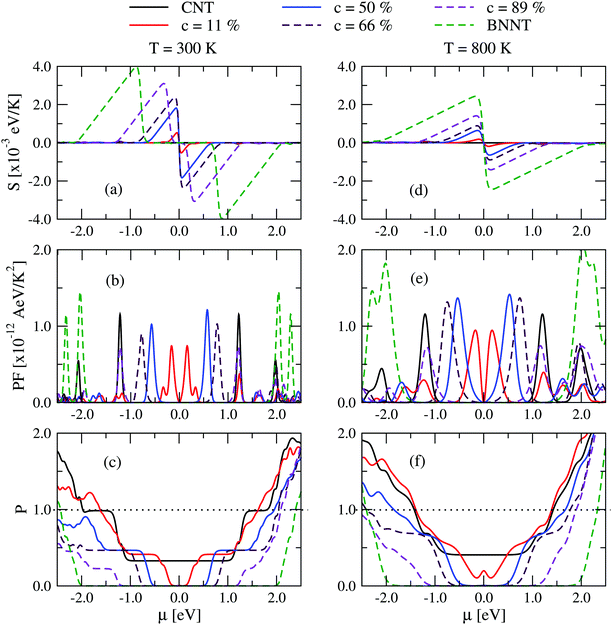
How do the previously discussed results for electron and phonon transport influence the thermoelectric response of the (6,6)-BNC heteronanotubes? For the sake of simplicity, we will only focus from now on on the helical nanotubes, since we do not expect strong qualitative changes for the case of BN stripes. In Fig. 4, the Seebeck coefficient (S) and the power factor (PF) of the helical tubes are shown as a function of the chemical potential μ for various BN concentrations at 300 K and 800 K. Here, μ is positive for n-type doping and negative for p-type doping. The Seebeck coefficient displays a symmetric behavior with respect to the charge neutrality point (CNP, μ = 0.0 eV) and its maximum value (Smax) varies from 0.06 × 10−3 eV K−1 (pristine (6,6)-CNT) up to 4.0 × 10−3 eV K−1 (pristine (6,6)-BNNT) upon increasing the BN concentration (see Fig. 4(a)). The corresponding μ values (later referenced as μmax) of Smax move far from the CNP due to the continuous increase of the electronic bandgap (see Fig. 2(c)). In addition, the Seebeck coefficient first increases and then decreases after increasing the temperature, with μmax getting closer to the CNP (see Fig. S8 in the ESI†). This trend was also reported in single-wall CNTs45,47 and two-dimensional materials with puckered structures.41When combining the electronic conductance and Seebeck coefficients into the power factor (PF = S2G), we realize that unlike Smax(T), PFmax only increases as a function of the temperature (see Fig. 4(b and e)). A non-monotonous behavior of PF with respect to the doping concentration is also found. PFmax decreases for a concentration of 11%, and then it subsequently increases until a maximum value is reached at c = 50%. This effect is related to the fact that the reduction of the electronic conductance is larger compared to the increment in the Seebeck coefficient upon increasing the BN concentration in the helical tubes. Moreover, the mirror symmetry found in S(μ) is slightly broken in the power factor, having larger PF values for n-type doping. This asymmetry only happens for certain BN concentrations and it is a result of the hybridization of p orbitals from the helical BN and C domains, which affects the electron transmission probability associated with the conduction and valence bands (see Fig. S1 and S3 in the ESI†). It is worth noting that pristine (6,6)-BNNT displays a larger PF than (6,6)-CNT and the helical tubes, however, the n-type or p-type doping concentration needed to get this value is quite large (corresponding to μ ∼ 2.0 eV).
We next investigate the influence of varying chemical potential on the electronic (κel) and phononic (κph) components of the thermal conductance of the helical heteronanotubes. In Fig. 4(c) and (f), the ratio P = κel/κph is displayed at 300 K and 800 K, respectively. Corresponding to the increase of Eg (see Fig. 2 for comparison), the electronic thermal conductance also has an energy gap around the CNP. Moreover, P < 0.5 for small and large |μ| values, i.e., heat transport in helical (6,6)-BNC heteronanotubes is mainly dominated by phonons. This predominance is more evident at higher BN concentrations. However, it is worth noting that κel increases faster than κph after increasing the temperature and, hence, P → 1.0 (e.g., see Fig. 4(f) for the case of 800 K).
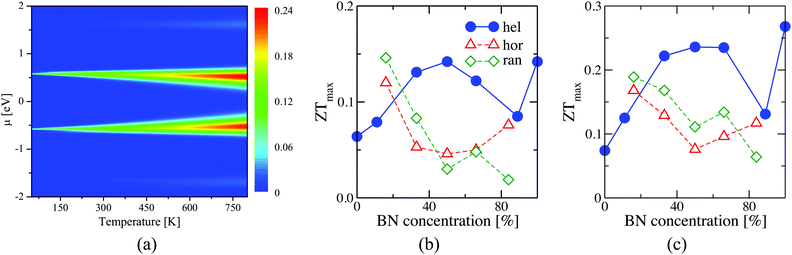
A heatmap showing the variation of the figure of merit ZT with chemical potential and temperature for c = 50% is shown in Fig. 5(a). Similar heatmaps for BN stripes and randomly doped (6,6)-BNC heteronanotubes are shown in the ESI† (see Fig. S7). ZT is enhanced by increasing the temperature (also for other BN arrangements). Fig. 5(b) and (c) show, as a summary, the figure of merit for two cuts (T = 300 and T = 800 K) along the concentration axis for all studied cases. For small BN concentrations, c < 20%, independent of the temperature, horizontally and randomly doped (6,6)-BNC heteronanotubes have larger ZTmax values than that of the helical ones. This is due to their higher power factor and lower phonon thermal conductance. Whilst for larger concentrations, their electron transport properties changed dramatically and helical (6,6)-BNC heteronanotubes show the highest ZTmax values with a maximal performance at c ∼ 50%. This maximal response was also observed in their power factor (see Fig. 4(b and e)). Thus, ZT reaches values of ∼0.14 at 300 K and ∼0.24 at 800 K, which are larger than those corresponding to pristine carbon nanotubes47 and functionalized graphene grain boundaries,40 but comparable to those of more complex carbon-based nanostructures.45,51 The obtained ZT values are also close to those values reported for hybrid graphene/boron-nitride nanoribbons.30 Hence, the ZT of (6,6)-CNTs can be enhanced by up to 2.3 times and 3.4 times its initial value at 300 K and 800 K, respectively, by modifying the pristine nanotube with BN helical stripes.
4 Conclusions
We have performed a DFTB–NEGF study of the thermoelectric transport properties of BNC heteronanotubes, focusing on the influence of BN concentration and the doping distribution pattern. Independent of the spatial atomic BN distribution, the electron and phonon transmission functions are reduced near the band edges and at high frequencies after increasing the BN concentration, respectively. These effects are stronger for randomly doped (6,6)-BNC heteronanotubes. For all doping patterns, (6,6)-CNT loses its metallic behavior and becomes semiconducting with a tunable electronic bandgap. Moreover, it was found that phonons are mainly responsible for heat transport in helical BNC heteronanotubes and the phonon thermal conductance at 300 K first decreases for small BN concentrations, remains constant for 30% < c < 80%, and then increases. The Seebeck coefficient of (6,6)-CNT is enhanced by increasing the doping concentration in helical (6,6)-BNC heteronanotubes, which, combined with the electron conductance, produces a non-monotonous behavior of PFmax with a maximal response at c = 50%. As a result, ZT of helical (6,6)-BNC heteronanotubes is larger than the corresponding values of horizontally and randomly doped nanotubes for BN concentrations larger than ∼20%. ZT values of CNTs are increased by up to 2.3 times and 3.4 times their initial value at 300 K and 800 K, correspondingly. Despite the obtained ZT values, we expect our results to shed light on the relevance of doping engineering to control the electron and phonon transport of BNC heteronanotubes and, hence, design potential nanoscale thermoelectric devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
L. M. S. gratefully acknowledges the International Max Planck Research School Dynamical processes in atoms, molecules and solids and the Deutscher Akademischer Austauschdienst (DAAD) for the financial support. G. C. S. and C. V. L. are grateful to the National Council of Science and Technology (CONCYTEC) from Peru for the financial support through the Doctoral Program for Peruvian Universities (No. 218-2014-FONDECYT) and the Peruvian Excellence Center Program, respectively. This work has also been partly supported by the German Research Foundation (DFG) within the Cluster of Excellence “Center for Advancing Electronics Dresden”. We acknowledge the Center for Information Services and High Performance Computing (ZIH) at TU Dresden for computational resources. Open Access funding provided by the Max Planck Society.References
- S. Iijima, Nature, 1991, 354, 56 CrossRef CAS.
- R. S. Ruoff and D. C. Lorents, Carbon, 1995, 33, 925–930 CrossRef CAS.
- R. Saito, G. Dresselhaus and M. Dresselhaus, Physical properties of carbon nanotubes, Imperial College Press, 1998 Search PubMed.
- P. Ajayan, Chem. Rev., 1999, 99, 1787–1800 CrossRef CAS PubMed.
- E. Zurek and J. Autschbach, J. Am. Chem. Soc., 2004, 126, 13079–13088 CrossRef CAS PubMed.
- A. Nojeh, G. W. Lakatos, S. Peng, K. Cho and R. F. W. Pease, Nano Lett., 2003, 3, 1187–1190 CrossRef CAS.
- C. Zhou, J. Kong, E. Yenilmez and H. Dai, Science, 2000, 290, 1552–1555 CrossRef CAS PubMed.
- A. Bachtold, P. Hadley, T. Nakanishi and C. Dekker, Science, 2001, 294, 1317–1320 CrossRef CAS PubMed.
- O. Stephan, P. M. Ajayan, C. Colliex, P. Redlich, J. M. Lambert, P. Bernier and P. Lefin, Science, 1994, 266, 1683–1685 CrossRef CAS PubMed.
- J. Zhang and C. Wang, J. Phys. D: Appl. Phys., 2016, 49, 155305 CrossRef.
- R.-L. Zhong, H.-L. Xu and Z.-M. Su, Phys. Chem. Chem. Phys., 2016, 18, 13954–13959 RSC.
- W. An and C. H. Turner, J. Phys. Chem. Lett., 2010, 1, 2269–2273 CrossRef CAS.
- A. Du, Y. Chen, Z. Zhu, G. Lu and S. C. Smith, J. Am. Chem. Soc., 2009, 131, 1682–1683 CrossRef CAS PubMed.
- Z. Guan, W. Wang, J. Huang, X. Wu, Q. Li and J. Yang, J. Phys. Chem. C, 2014, 118, 28616–28624 CrossRef CAS.
- J. da Rocha Martins and H. Chacham, ACS Nano, 2011, 5, 385–393 CrossRef PubMed.
- Y. Wang, G. Huang, J. Zhang and Q. Shao, J. Mol. Model., 2014, 20, 2371 CrossRef PubMed.
- K. Suenaga, C. Colliex, N. Demoncy, A. Loiseau, H. Pascard and F. Willaime, Science, 1997, 278, 653–655 CrossRef CAS.
- S. Enouz, O. Stéphan, J.-L. Cochon, C. Colliex and A. Loiseau, Nano Lett., 2007, 7, 1856–1862 CrossRef CAS PubMed.
- E. Iyyamperumal, S. Wang and L. Dai, ACS Nano, 2012, 6, 5259–5265 CrossRef CAS PubMed.
- L. Liao, K. Liu, W. Wang, X. Bai, E. Wang, Y. Liu, J. Li and C. Liu, J. Am. Chem. Soc., 2007, 129, 9562–9563 CrossRef CAS PubMed.
- X. Wei, M.-S. Wang, Y. Bando and D. Golberg, ACS Nano, 2011, 5, 2916–2922 CrossRef CAS PubMed.
- M. Terrones, D. Golberg, N. Grobert, T. Seeger, M. Reyes-Reyes, M. Mayne, R. Kamalakaran, P. Dorozhkin, Z.-C. Dong, H. Terrones, M. Roehle and Y. Bando, Adv. Mater., 2003, 15, 1899–1903 CrossRef CAS.
- R. Sen, B. Satishkumar, A. Govindaraj, K. Harikumar, G. Raina, J.-P. Zhang, A. Cheetham and C. Rao, Chem. Phys. Lett., 1998, 287, 671–676 CrossRef CAS.
- L. Algharagholy, T. Pope, Q. Al-Galiby, H. Sadeghi, S. W. D. Bailey and C. J. Lambert, J. Mater. Chem. C, 2015, 3, 10273–10276 RSC.
- X. Blase, J.-C. Charlier, A. D. Vita and R. Car, Appl. Phys. Lett., 1997, 70, 197–199 CrossRef CAS.
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114 CrossRef CAS PubMed.
- H. Alam and S. Ramakrishna, Nano Energy, 2013, 2, 190–212 CrossRef CAS.
- J. L. Blackburn, A. J. Ferguson, C. Cho and J. C. Grunlan, Adv. Mater., 2018, 30, 1704386 CrossRef PubMed.
- M. Terrones, A. Jorio, M. Endo, A. M. Rao, Y. A. Kim, T. Hayashi, H. Terrones, J.-C. Charlier, G. Dresselhaus and M. S. Dresselhaus, Mater. Today, 2004, 7, 30–45 CrossRef CAS.
- K. Yang, Y. Chen, R. D'Agosta, Y. Xie, J. Zhong and A. Rubio, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 045425 CrossRef.
- C. Lin, X. Zhang and Z. Rao, Nano Energy, 2017, 38, 249–256 CrossRef CAS.
- L. Medrano Sandonas, G. Cuba-Supanta, R. Gutierrez, A. Dianat, C. V. Landauro and G. Cuniberti, Carbon, 2017, 124, 642–650 CrossRef CAS.
- C. W. Chang, W.-Q. Han and A. Zettl, Appl. Phys. Lett., 2005, 86, 173102 CrossRef.
- S. Jiuxu, Y. Yintang, L. Hongxia and G. Lixin, J. Semicond., 2011, 32, 042003 CrossRef.
- J. Yuan, Y. Hu, J. Liao, J. Zhong and Y. Mao, Mater. Des., 2016, 95, 641–647 CrossRef CAS.
- Z.-Y. Zhang, C. Miao and W. Guo, Nanoscale, 2013, 5, 11902–11909 RSC.
- A. C. M. Carvalho, C. G. Bezerra, J. A. Lawlor and M. S. Ferreira, J. Phys.: Condens. Matter, 2014, 26, 015303 CrossRef CAS PubMed.
- M. Machado, T. Kar and P. Piquini, Nanotechnology, 2011, 22, 205706 CrossRef CAS PubMed.
- J. P. Guedes, F. de Brito Mota, S. Azevedo and C. M. C. de Castilho, Eur. Phys. J. B, 2015, 88, 236 CrossRef.
- L. Medrano Sandonas, R. Gutierrez, A. Pecchia, A. Dianat and G. Cuniberti, J. Self-Assem. Mol. Electron., 2015, 3, 1–20 CrossRef.
- L. Medrano Sandonas, D. Teich, R. Gutierrez, T. Lorenz, A. Pecchia, G. Seifert and G. Cuniberti, J. Phys. Chem. C, 2016, 120, 18841–18849 CrossRef CAS.
- L. Medrano Sandonas, R. Gutierrez, A. Pecchia, G. Seifert and G. Cuniberti, Phys. Chem. Chem. Phys., 2017, 19, 1487–1495 RSC.
- T. Frauenheim, G. Seifert, M. Elsterner, Z. Hajnal, G. Jungnickel, D. Porezag, S. Suhai and R. Scholz, Phys. Status Solidi B, 2000, 217, 41–62 CrossRef CAS.
- G. Seifert, J. Phys. Chem. A, 2007, 111, 5609–5613 CrossRef CAS PubMed.
- T. Lehmann, D. A. Ryndyk and G. Cuniberti, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 035418 CrossRef.
- L. Medrano Sandonas, H. Sevinçli, R. Gutierrez and G. Cuniberti, Adv. Sci., 2018, 5, 1700365 CrossRef PubMed.
- J.-W. Jiang, J.-S. Wang and B. Li, J. Appl. Phys., 2011, 109, 014326 CrossRef.
- A. Pecchia, G. Penazzi, L. Salvucci and A. D. Carlo, New J. Phys., 2008, 10, 065022 CrossRef.
- W. Zhang, T. S. Fisher and N. Mingo, Numer. Heat Transfer, Part B, 2007, 51, 333–349 CrossRef CAS.
- E. Pop, D. Mann, Q. Wang, K. Goodson and H. Dai, Nano Lett., 2006, 6, 96–100 CrossRef CAS PubMed.
- L. Liang, E. Cruz-Silva, E. C. Girão and V. Meunier, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 115438 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp05592k |
| This journal is © the Owner Societies 2019 |