Open Access Article
Open Access ArticleElucidating DNA binding of dithienylethenes from molecular dynamics and dichroism spectra†
Mathieu
Linares
 ab,
Haofan
Sun
ac,
Michal
Biler
ab,
Haofan
Sun
ac,
Michal
Biler
 a,
Joakim
Andréasson
a,
Joakim
Andréasson
 d and
Patrick
Norman
d and
Patrick
Norman
 *a
*a
aDepartment of Theoretical Chemistry and Biology, School of Engineering Sciences in Chemistry, Biotechnology and Health, KTH Royal Institute of Technology, SE-106 91 Stockholm, Sweden. E-mail: panor@kth.se
bSwedish e-Science Research Centre (SeRC), KTH Royal Institute of Technology, SE-104 50 Stockholm, Sweden
cShanghai Key Laboratory of Functional Materials Chemistry, Department of Chemistry and Molecular Engineering, East China University of Science and Technology, Shanghai 200237, China
dDepartment of Chemistry and Chemical Engineering, Chalmers University of Technology, 41296 Göteborg, Sweden
First published on 16th October 2018
Abstract
DNA binding modes of the stereoisomeric rotamers of two dithenylethene derivatives (DTE1 and DTE2) representing candidate molecular photoswitches of great promise for photopharmacology and nanotechnology have been identified and characterized in terms of their binding energies and electronic circular dichroism (CD) responses. In the open form, two binding modes are identified namely minor-groove binding of the lowest-energy conformer with an anti-parallel arrangement of methyl groups and major-groove double-intercalation of the P-enantiomers of an intermediate-state rotamer. Only the latter binding mode is found to be enantiomerically selective and expected to have an overall negative linear dichroism (LD) as observed in the experiment for DTE1 (Angew. Chem., Int. Ed., 2013, 52, 4393). In the closed form, the most favorable binding mode is found to be minor groove binding. Also this binding mode is found to be enantiomerically selective and for DTE1, it is the M-enantiomer that binds the strongest, showing a positive theoretical signature CD band in the long wavelength region with origin in pyridinium ligands. The theoretical CD spectrum is found to be in good agreement with the experimental one, which provides an indirect evidence for a correct identification of the binding mode in the closed form.
1 Introduction
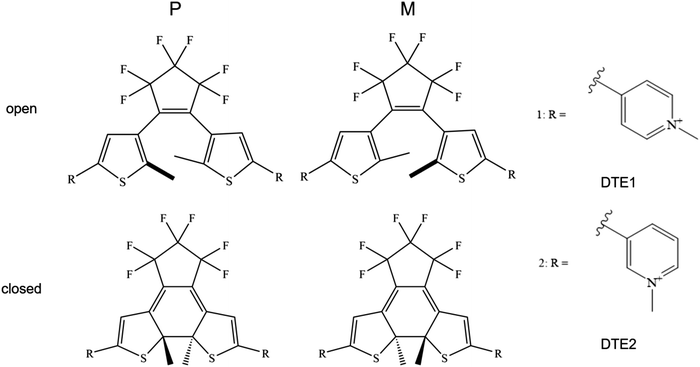
Being suitable for photonic device technology, dithienylethene (DTE) derivatives have been under investigation for many years and the photochromic cyclization has been studied in liquid and solid phases.1,2 These compounds exist as two constitutional isomers namely open and closed. The typically colorless open form absorbs light in the UV region only, and is isomerized to the closed colored form under UV light exposure. The reaction is reversed photonically by exposure to visible light, and in principle also by heat, as the open isomer is thermodynamically stable. However, the thermal isomerization is often very slow, implying very good thermal stability of both isomeric forms. Other appealing properties of this class of photoswitches are high conversion efficiencies of the photoisomerizations, good resistance towards photofatigue, and high reactivity in the solid state. The open isomer exists in two conformations: one conformer with the two aryl rings in mirror symmetry (in parallel orientation) and another that displays C2 symmetry (in antiparallel orientation). Due to orbital symmetry arguments, only the antiparallel conformer can undergo the photoinduced electrocyclization reaction to the closed isomer. However, the interconversion between the two conformers occurs much faster than the timescale of a typical isomerization experiment, implying that the two conformers can be considered as always being equilibrated (typically 50/50).DTE derivatives are being identified as potential candidates for photopharmacology—a research field in which light is being used to control the interactions between small molecules and biorelevant systems such as DNA, proteins, and cell membranes.3–5 As for DNA as the target,6 Feringa and co-workers designed a DTE switch with two terminal amino groups which, however, was found to bind to DNA in both the open and closed forms.7 This was shown to be the case also in the studies by the groups of Andréasson8 and Gamez,9 respectively, in which the binding mode was demonstrated to depend both on the DTE structure and the isomeric form. Moreover, the circular dichroism (CD) signal of the complex displayed an attenuation in the region of the DNA bands and thus demonstrating that both components of the complex mutually influence each other's structure—the DNA helix induces chirality in the switch and the switch modifies the structure of the DNA—and when the pH was increased, the switch lost its ability to bind, indicating that electrostatic interactions between protonated amines and the negatively charged phosphate backbone represent the dominant driving force for the binding to DNA.7 The work by Andréasson reported the first observation of enantioselectivity in the closing reaction of DTE bound to DNA,8 whereas the work by Gamez focused on DTE diplatinum(II) complexes that showed altered cytotoxicity upon photoisomerization.9 Moreover, photocontrolled DNA-binding is identified as a means also to control processes of high generic value for nanotechnology and materials applications.6 DNA origami is a prime example, and it has been shown that small-molecule binding to these nano-sized architectures results in substantial changes in the geometry.10,11 Of course, being able to control the binding event by light as an external stimulus adds to the appeal, and extrapolation to, e.g., light-controlled release of chemical payloads from nano-sized DNA origami containers is tempting in this context. Requirements for such a scheme include either on/off-switching of the DNA-binding in concert with the isomerization or, alternatively, a change in the DNA binding mode.
It is the purpose of the present work to shed light on the microscopic details of the binding modes of supramolecular complexes formed between DNA and positively charged pyridine appended DTE structures. The study is motivated by the abovementioned DTE derivative previously reported by Andréasson, herein referred to as DTE1, for which the binding mode changes from intercalation to groove binding upon isomerization from the open isomer to the closed isomer.8 A similar derivative is also included (referred to herein as DTE2), where the position of the pyridinium nitrogen has been changed. Similarities/differences between DTE1 and DTE2 will be valuable for the design of future derivatives aiming at maximizing the differences in DNA-binding that follows upon photoisomerization.
As the primary tool for our study, we will make use of molecular dynamics (MD) simulations. The comparison between theory and experiment is indirect and made at the level of dichroism spectroscopies and we will consider minor and major groove bindings as well as different forms of intercalation.
2 Computational details
The R.E.D. program12 in conjunction with density functional theory (DFT) calculations at the level of B3LYP/cc-pVDZ13–16 were used to calculate electrostatic potential (ESP) charges for the various DTE species under study, see Fig. 1 for schematic illustrations of the molecular structures. Using the Amber software package,17 the LEaP module was used to generate topologies and initial coordinate files employing the general Amber force field (GAFF) and the NAB module was used to build a DNA double-strand of 20 adenine-thymine (AT) base-pairs. The force fields used for DNA and water were Parmbsc118 and TIP3P,19 respectively.MD simulations were performed under aqueous conditions at 300 K using Langevin dynamics and constant pressure periodic boundary with an average pressure of 1 atm and with isotropic position scaling using a Berendsen barostat. A cut-off of 12 Å was set for non-bonded interactions and counter ions were added in all cases as to ensure overall charge-neutrality in the systems. The trajectory simulations made for assessing the stability of binding modes between DTE1 or DTE2 and DNA were run for 100 ns. Average coulombic and van der Waals (vdW) interaction energies of the found stable binding sites were calculated by averaging the snapshots recorded every 10 ps over the last 5 ns (500 frames), 10 ns (1000 frames), 20 ns (2000 frames), and 30 ns (3000 frames). All statistics are presented in the ESI.†
All structures depicted in Fig. 1 and 2 were optimized using Kohn–Sham DFT at the level of B3LYP/cc-pVDZ13–16 with an inclusion made of D3 dispersion corrections.20 Transition states (TSs) found along the reaction paths were confirmed by analyses based on vibrational frequencies and intrinsic reaction coordinates (IRC). Solvent effects were taken into account using the implicit polarizable continuum model (PCM).
The dichroism responses were determined by means of time-dependent DFT at the level of B3LYP/aug-cc-pVDZ13–16 for the several found conformers. The presented spectra are based on the calculation of electric-dipole and magnetic-dipole transition moments. All quantum chemical calculations were performed with the Gaussian program.21
3 Results and discussion
3.1 Conformational analysis of DTE
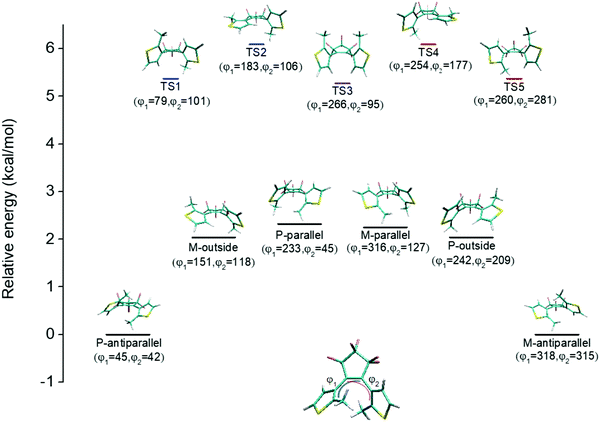
An illustration of the molecular structures of the DTE derivatives under study in their P- and M-enantiomeric forms as well as their open and closed forms is presented in Fig. 1. We will refer to the species with a hydrogen ligand (R = H) as the core DTE and by DTE1 and DTE2, we denote two species with a methyl-pyridinium ligand where the nitrogen atom is found in the para and meta positions, respectively. In the open form, both enantiomers display a conformational degree of freedom associated with dihedral rotations of the C–C bonds that bind two thiophenes–the corresponding angles are denoted by φ1 and φ2 in Fig. 2. In Fig. 1, we schematically depict an anti-parallel placement of the methyl groups of the two thiophenes but a parallel placement is also possible, in which case one of the methyl groups points outwards of the molecule. The third possibility is for both methyl groups to point outwards and we will refer to such conformations as outside.The anti-parallel rotamers are found to be the lowest in energy, see Fig. 2. We first set out to map the path and the intermediates for the reaction going from the P- to the M-form of the anti-parallel rotamers of the core DTE. We find this reaction to have four intermediate states and correspondingly five transition states and an overview of the changes in the dihedral angles along the path is found in Fig. 3. The first barrier to cross the transition state TS1 and go from P-antiparallel to M-outside is the highest and amounts to 5.3 kcal mol−1 at the adopted level of theory. The subsequent barriers to cross transition states TS2–TS5 amount to about 3–4 kcal mol−1. The TS1-barrier is sufficiently high as to prevent this reaction to occur on the short timescale that is accessible in MD simulations, see the ESI† for the detailed conformer population histograms of these simulations. In the experiment, on the other hand, timescales are longer and these barriers will be passed so that a racemic mixture of the open form of DTE in solution will always be maintained even when a preferential binding occurs to a host molecule such as DNA. In such a case, the dichroism signal will stem from only the biomarker complex. Furthermore, the intermediate state rotamers give rise to additional DNA binding opportunities in terms of more elaborate two-sided (or double) intercalation as we shall see in the subsequent section.
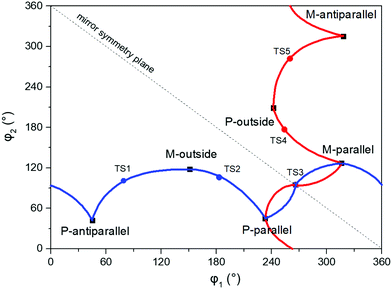 | ||
| Fig. 3 Changes in the dihedral angles φ1 and φ2 during the reaction going from the P-antiparallel to the M-antiparallel form of DTE. Points on the red and blue curves on opposite sides of the line indicating mirror symmetry represent enantiomers. See Fig. 1 for a definition of the dihedral angles. | ||
3.2 DNA binding of DTE
Our assessment of the binding of DTE to DNA is based on MD simulations on the timescale ranging up to 100 ns. On this timescale, we observe unbiased docking of DTE in the minor groove of DNA with the formation of stable complexes with large binding energies—Fig. S12 in the ESI† shows an example of unbiased docking of DTE1. Here, unbiased refers to the formation of a DNA–DTE complex starting from a separated and randomly positioned biomarker and target host. This timescale is, on the other hand, not sufficiently long to spontaneously form complexes based on intercalation, so in our study of such binding sites, we manually inserted DTE in between two base-pair dimers and relaxed the structure before starting the MD simulations. In fact, major groove binding was also never observed from unbiased MD simulations and also in this case we needed to create initial structures for the DNA–DTE complex. However, apart from a single variant of DTE namely the P-conformer of DTE1 in the closed form with an anti-parallel arrangement of the methyl groups, we could not observe any stable major groove binding of DTE to DNA—Fig. S13 in the ESI† shows an example of an escape of DTE1 from the major groove. In this single case where a stable complex was observed on the timescale of the simulation, the binding energy was found to be very small compared to other binding site arrangements and we therefore rule out major groove binding as an alternative that needs further consideration.Before continuing, let us briefly discuss our chosen way to assess and rank the different binding sites. The first and foremost criterion from which a binding site can be unambiguously characterized from MD is of course that the complex remains stable for the entire duration of the simulations. Given that a binding site passes this binary test, it becomes necessary to create some sort of scoring function to estimate the binding affinity and to compare different binding sites. Several schemes have been developed for this purpose and we have chosen to adopt a scoring function from the force field class. We sum the force field energies associated with electrostatic and van der Waals intermolecular interactions. Minus the value of this summed interaction energy is presented in Table 1 as a binding energy and this becomes our scoring function. It must be remembered, however, that intramolecular energetic penalties associated with strain is not accounted for in our scheme and clearly caution is called for in comparing for instance groove binding with intercalation.
| DTE1 | DTE2 | |||||||
|---|---|---|---|---|---|---|---|---|
| Open | Closed | Open | Closed | |||||
| P | M | P | M | P | M | P | M | |
| a Double intercalation is found stable only with a parallel arrangement of the methyl groups. | ||||||||
| MiGB | 221 ± 29 | 234 ± 26 | 220 ± 19 | 249 ± 21 | 230 ± 37 | 227 ± 33 | 279 ± 22 | 259 ± 16 |
| MaGB | — | — | 60 ± 40 | — | — | — | — | — |
| MiGI | — | 186 ± 25 | 163 ± 21 | 201 ± 23 | 150 ± 19 | 168 ± 24 | — | — |
| MaGI | 131 ± 21 | 186 ± 26 | 156 ± 11 | 216 ± 20 | 180 ± 21 | 194 ± 15 | 155 ± 10 | 152 ± 11 |
| MaGdI | 233 ± 16a | — | — | — | 255 ± 14a | — | — | — |
A strong minor groove binding is found for both the P- and M-conformers of DTE1 and DTE2 in the open as well as closed forms—the binding energies are presented in Table 1 and they are seen to amount to in between 220 and 280 kcal mol−1. In all cases, minor and major groove intercalations are substantially less favorable showing binding energies in between 130 and 220 kcal mol−1, so the MD simulations unambiguously predict minor groove binding before single intercalation. In the open form, there is no significant difference in affinities found when comparing the two species whereas, in the closed form, the P-conformer of DTE2 binds particularly strongly in the minor groove with a binding energy amounting to nearly 280 kcal mol−1.
We have also investigated the possibility for the open forms of DTE to bind to DNA by means of double intercalation in any of the conformational forms of the intermediate states identified in the reaction scheme in Fig. 2. We attempted to bind both the P- and M-conformers with parallel and outside arrangements of the methyls but it turned out that we could only find stable binding sites for the P-conformers of DTE1 and DTE2 with a parallel arrangement of the methyls. For these complexes, the binding energies reported in Table 1 for double intercalation are found to be in between 230 and 260 kcal mol−1, which is in the same region as the binding energies reported for minor groove binding. Double intercalation is thus seen to be a competitive binding mode for the open form of both DTE1 and DTE2.
When comparing coulombic and vdW interactions, the former are without exception 2–4 times stronger in all revealed binding sites, see Tables S4–S6 in the ESI† for separate Coulomb and vdW interaction energies. This is in agreement with the experimental evidence for a pH-dependent ability of DTE to bind to DNA as the coulombic interactions are increased at a low pH-value due to protonation.
3.3 DTE dichroism responses
In probing DNA by means of studying the ππ*-transitions of conjugated biomarkers in CD spectroscopy, there are several mechanisms to be considered. It was recently demonstrated that the induced circular dichroism (ICD) of an achiral minor-groove-bound probe named DAPI, which has been extensively used in biological applications, has several potential sources: (i) the molecular structure changes upon groove binding, (ii) chiral imprint on the electronic structure, (iii) charge-transfer contributions to electronic transitions, (iv) off-resonant excitonic coupling between the probe and the host, and (v) resonant excitonic coupling between adjacent groove-bound probes.22 In the case of DTE binding to DNA, we believe that the situation is different. First and foremost, the rotamers of DTE represent chiral probes so that the signal response does not rely on the sensitive ICD effect. For the open-form species, this will imply that the CD response becomes a result of the differential binding affinities of the enantiomers because, as mentioned above, when free in solution, the open-form enantiomers will always become equilibrated and contain a racemic mixture of DTE so that the signal responses stem from only the bound probes. However, for the closed-form species, this argument does not hold since an enantiomeric equilibration will not take place for the probes in solution, and unless the signal contribution from the solution is removed in the experiment, it is not possible to make a direct comparison to the theoretical results reported in the present work. Second, the experiment shows that with a 9.1 μM concentration of DTE1, the CD response first increases and thereafter saturates upon increasing the concentration of DNA up to a base-pair concentration of about 400 μM.8 We interpret this result as a sign that resonant excitonic coupling is not a key contributor to the long wavelength bands associated with DTE, because we would otherwise have seen a signal decrease as distances between the bound probes would statistically have increased as a result of an increased base-pair to probe ratio. Third, whereas DAPI is known to be solely a minor-groove binder, there are relevant double-intercalation major-groove binding-modes found in our MD simulations and in such cases the large changes in the molecular structure will strongly affect the CD responses.Taken into account the above considerations for DTE, it is argued that a quantitative analysis of CD spectra in the long wavelength region (λ > 300 nm) could be achieved by extracting the molecular structures of DTE from the trajectories of the molecular dynamics simulations and calculating the response properties of the probe in isolation. However, in order to reach an accurate sampling of the configuration space, this snapshot approach comes at a steep computational cost. Even in the seemingly simple case of minor-groove binding, it would become relevant to sample alternative DNA primary structures and consider the set of different minor-groove sites as to obtain an improved model of experimental conditions (the referred-to experiment used calf thymus DNA8). Instead we argue that the changes in the molecular structures of DTE upon minor groove-binding are rather small so that we can make reference to the CD spectra calculated at optimized geometries as representing the corresponding statistically averaged spectra. The hereby obtained spectra will not reach a quantitative accuracy and we will restrict ourselves to a qualitative comparison to the experimental results for the key signature bands. In the much more complicated situation of major-groove double intercalation (MaGdI), we must remember that the binding sites reported in the previous sections were found by manual insertion of DTE into a single site of our specific DNA sequence. Although we believe to convincingly have demonstrated MaGdI to be a relevant binding mode, we are nowhere near having reached an accurate sampling of all the possible double-intercalation sites that may be probed in the experiment. For this reason, we refrain from calculating CD spectra in the found MaGdI binding sites.
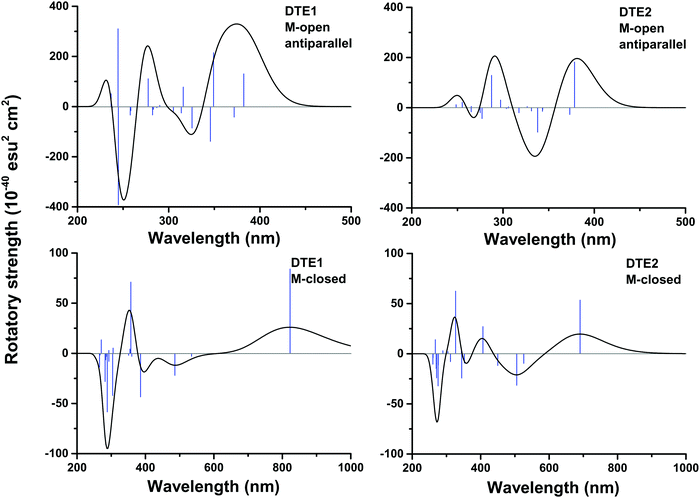
In Fig. S16 of the ESI†, the theoretical CD spectra are found for the P- and M-enantiomers of the core DTE in the open and closed forms. In the open M-form of the lowest-energy anti-parallel conformer, the signature band for core DTE is found in the region of 325–350 nm in terms of a strong negative band. When compared to the corresponding spectrum for DTE1 in Fig. 5 (upper left panel), the signature band is instead positive and positioned around 380 nm. The explanation for this discrepancy is that electronic transitions associated with the pyridinium ligands have entered the spectrum in DTE1—the three lowest-energy transitions in the spectrum (out of which two have positive rotatory strengths) belong to this category, whereas the fourth transition in DTE1 is associated with the core DTE moiety and corresponds to the negative band in Fig. S16 (ESI†).
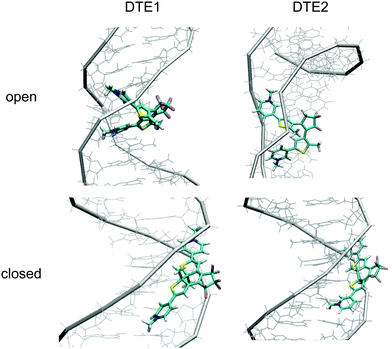
The positioning at 380 nm of the theoretical CD signature band of DTE1 agrees reasonably well with the experiment, where the result for λmax in the UV/vis spectrum is circa 355 nm and a further red-shift is observed upon binding to DNA.8 Moreover, the absence of positive bands in the experimental linear dichroism (LD) spectra for DTE1 provides strong support for binding of DTE1 to DNA based on intercalation rather than groove binding.8 As we have seen above, minor groove intercalation is energetically very unfavorable and major groove double intercalation (MaGdI) occurs only for the P-enantiomer with a parallel positioning of the methyl groups as illustrated in the two upper panels of Fig. 4 for DTE1 and DTE2, respectively. In comparison to DTE1, the MaGdI binding mode of DTE2 is even more energetically favorable and this theoretical result in combination with the experimental fact (LD spectrum of DTE1) thus suggests that both DTE1 and DTE2 bind to DNA by means of MaGdI. This proposed double-intercalation binding site is associated with large mutual distortions of the molecular structure of the DNA–DTE complex and it would certainly affect the CD bands associated with DNA (λ < 300 nm) as observed in the experiment.
For the closed form of DTE1, the experimental LD spectrum suggests groove binding8 and the theoretical binding energies presented in Table 1 agree with this observation. The theoretical CD spectrum of the P-enantiomer of the closed form of core DTE shows a positive signature band around 580 nm, see Fig. S16 (lower left panel) in the ESI.† However, just as in the open form of DTE, it is clear that the pyridinium ligands have a qualitative impact on the signature bands in the CD spectra of the closed-form species, because, as seen in Fig. 5 (lower panels), the signature bands of the CD spectra for the M-enantiomers of DTE1 and DTE2 show positive signature bands around 800 and 700 nm, respectively. Since the M-conformer of DTE1 shows a larger minor groove binding energy compared to the P-conformer (249 versus 220 kcal mol−1), it is this positive band around 800 nm that is the relevant one for a comparison with the experimentally observed positive band at 700 nm.8 But as stated above, a direct comparison of theoretical and experimental CD responses would require purification of the DNA–DTE1 complex in the experiment as to rid the CD spectrum from any contributions from the remaining solvated probes.
4 Summary
The DNA binding of two dithienylethene derivatives (DTE1 and DTE2) in their open and closed forms has been studied. The rotamers reached in the thermally driven open-form stereoisomerizations of DTE1 and DTE2 have been mapped and an anti-parallel arrangement of methyl groups is shown to be the lowest in energy and to bind to DNA in the minor groove. However, the intermediate rotamers of DTE1 and DTE2 in their respective P-form with a parallel arrangement of methyl groups are shown to bind to DNA with a competitive binding energy by means of major-groove double-intercalation. In the closed form and based on the results of binding energies, the binding to DNA is shown to be enantiomerically selective, favoring the M-form of DTE1 and the P-form of DTE2.The CD spectra are determined for DTE1 and DTE2 in the open and closed forms and the signature bands associated with the lowest electronic ππ*-transitions fall in the regions of 350–400 and 700–850 nm for the open and closed forms, respectively. These transitions are shown to originate from the pyridinium ligands. For the M-enantiomer of DTE1 and the P-enantiomer of DTE2 in the closed form, the signature CD bands in the region of 700–850 nm are found to be positive and negative, respectively. Future measurements of the CD responses for the DNA–DTE complexes without contributions from the solvent environment would provide a strong evidence as to whether or not a correct theoretical discrimination has been achieved for the enantiomerically selective binding.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the Swedish Research Council (Grant No. 621-2014-4646) and the Swedish e-Science Research Centre (SeRC) is acknowledged. The secondment of H. S. at KTH Royal Institute of Technology was financed by the China Scholarship Council (CSC) (201706745036). The calculations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Centre (NSC) and the PDC Center for High Performance Computing (PDC), Sweden.References
- M. Irie, T. Fukaminato, K. Matsuda and S. Kobatake, Chem. Rev., 2014, 114, 12174 CrossRef CAS.
- J. Zhang and H. Tian, Adv. Opt. Mater., 2018, 6, 1701278 CrossRef.
- C. Brieke, F. Rohrbach, A. Gottschalk, G. Mayer and A. Heckel, Angew. Chem., Int. Ed., 2012, 51, 8446 CrossRef CAS PubMed.
- W. A. Velema, W. Szymanski and B. L. Feringa, J. Am. Chem. Soc., 2014, 136, 2178 CrossRef CAS.
- J. Broichhagen, J. A. Frank and D. Trauner, Acc. Chem. Res., 2015, 48, 1947 CrossRef CAS.
- A. S. Lubbe, W. Szymanski and B. L. Feringa, Chem. Soc. Rev., 2017, 46, 1052 RSC.
- A. Mammana, G. T. Carroll, J. Areephong and B. L. Feringa, J. Phys. Chem. B, 2011, 115, 11581 CrossRef CAS.
- T. C. S. Pace, V. Müller, S. Li, P. Lincoln and J. Andréasson, Angew. Chem., Int. Ed., 2013, 52, 4393 CrossRef CAS.
- A. Presa, L. Barrios, J. Cirera, L. Korrodi-Gregório, R. Pérez-Tomás, S. J. Teat and P. Gamez, Inorg. Chem., 2016, 55, 5356 CrossRef CAS.
- H. Chen, H. Zhang, J. Pan, T.-G. Cha, S. Li, J. Andréasson and J. H. Choi, ACS Nano, 2016, 10, 4989 CrossRef CAS.
- H. Chen, R. Li, S. Li, J. Andréasson and J. H. Choi, J. Am. Chem. Soc., 2017, 139, 1380 CrossRef CAS PubMed.
- F.-Y. Dupradeau, A. Pigache, T. Zaffran, C. Savineau, R. Lelong, N. Grivel, D. Lelong, W. Rosanski and P. Cieplak, Phys. Chem. Chem. Phys., 2010, 12, 7821 RSC.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007 CrossRef.
- D. A. Case, V. Babin, J. T. Berryman, R. M. Betz, Q. Cai, D. S. Cerutti, I. T. E. Cheatham, T. A. Darden, R. E. Duke, H. Gohlke, A. W. Goetz, S. Gusarov, N. Homeyer, P. Janowski, J. Kaus, I. Kolossváry, A. Kovalenko, T. S. Lee, S. LeGrand, T. Luchko, R. Luo, B. Madej, K. M. Merz, F. Paesani, D. R. Roe, A. Roitberg, C. Sagui, R. Salomon-Ferrer, G. Seabra, C. L. Simmerling, W. Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu and P. A. Kollman, Amber 14, University of California, San Francisco, 2014 Search PubMed.
- I. Ivani, P. D. Dans, A. Noy, A. Pérez, I. Faustino, A. Hospital, J. Walther, P. Andrio, R. Goñi, A. Balaceanu, G. Portella, F. Battistini, J. L. Gelpí, C. González, M. Vendruscolo, C. A. Laughton, S. A. Harris, D. A. Case and M. Orozco, Nat. Methods, 2016, 13, 55 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, “Gaussian16 Revision B.01,” Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- N. Holmgaard List, J. Knoops, J. Rubio-Magnieto, J. Idé, D. Beljonne, P. Norman, M. Surin and M. Linares, J. Am. Chem. Soc., 2017, 139, 14947 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp05326j |
| This journal is © the Owner Societies 2019 |