Molecular synthons for accurate structural determinations: the equilibrium geometry of 1-chloro-1-fluoroethene
Abstract
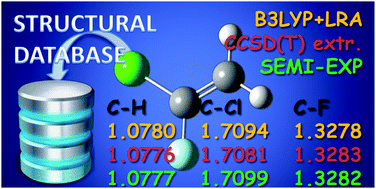
The equilibrium structure for 1-chloro-1-fluoroethene is reported. The structure has been obtained by a least-squares fit procedure using the available experimental ground-state rotational constants of eight isotopologues. Vibrational effects have been removed from the rotational constants using the vibration–rotation interaction constants derived from computed quadratic and cubic force fields obtained with the required quantum chemical calculations carried out by using both coupled cluster and density functional theory. The semi-experimental geometry obtained in this way has been also compared with the corresponding theoretical predictions obtained at the CCSD(T) level after extrapolation to the complete basis set limit and inclusion of core-valence corrections. These results allow completion of the molecular geometries of the isomers of chlorofluoroethene in addition to the cis and trans forms of 1-chloro-2-fluoroethene already published.
- This article is part of the themed collection: Challenges in spectroscopy: accuracy vs interpretation from isolated molecules to condensed phases


 Please wait while we load your content...
Please wait while we load your content...