Evaluating rotation diffusion properties of molecules from short trajectories†
Abstract
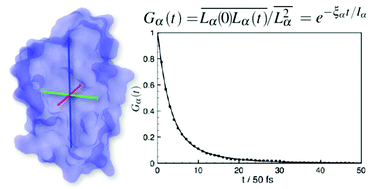
We show that under proper assumptions it is possible to estimate with good precision the principal values of the rotational diffusion tensor of proteins from the analysis of short (up to 2–3 ns) molecular dynamics trajectories. We apply this analysis to a few model cases: three polyalanine peptides (2, 5, and 10 aminoacids), the fragment B3 of protein G (GB3), the bovine pancreatic trypsin inhibitor (BPTI), the hen egg-white lysozyme (LYS), the B1 domain of plexin (PB1), and thrombin. The protocol is based on the analysis of the global angular momentum autocorrelation functions, complementing the standard approach based on rotational autocorrelation functions, which requires much longer trajectories. A comparison with values predicted by hydrodynamic modeling and available experimental data is presented.
- This article is part of the themed collection: Challenges in spectroscopy: accuracy vs interpretation from isolated molecules to condensed phases


 Please wait while we load your content...
Please wait while we load your content...