Aggregation of lactic acid in cold rare-gas matrices and the link to solution: a matrix isolation-vibrational circular dichroism study†
Abstract
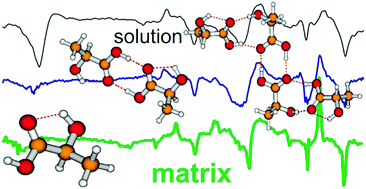
The matrix isolation (MI) technique has been utilized with vibrational circular dichroism (VCD) spectroscopy to obtain MI-VCD spectra of lactic acid (LA) in cold argon matrices, in addition to their MI-IR spectra. The experiments have been done at three different deposition temperatures (10 K, 16 K and 24 K) under different Ar flow rates so that different degrees of LA self-aggregation occur. The structural and spectral investigations of the LA monomer and the larger (LA)2,3,4 aggregates have been undertaken at three levels of theory (B3LYP/6-311++G(2d,p), B3LYP-D3BJ/6-311++G(2d,p) and B3LYP-D3BJ/def2-TZVPD) to evaluate the effects of dispersion correction and basis sets on optimized structures, relative conformer energies, and IR/VCD spectral features. Interestingly, the relative conformer energies vary considerably with and without dispersion correction, especially when the molecule gets larger and when it is placed in solution. Such uncertainties in the relative energies and in the vibrational band positions and IR/VCD intensities highlight the challenges in interpreting experimental spectroscopic data, especially those obtained in solution. With the narrow MI-IR band width and highly characteristic MI-VCD spectral features and the trend observed at three temperatures, we have been able to correlate the spectral features confidently to those of the LA monomer and the larger (LA)2,3,4 aggregates, with the aid of theoretical modeling. Finally, by noting the similarity of MI-IR and especially MI-VCD features obtained at 24 K with those of the 0.2 M solution, and with the aid of spectral simulation at the B3LYP-D3BJ/def2-TZVPD level, a composition of LA aggregates dominated by the LA tetramer and trimer has been identified. This conclusion differs from the previous reports where the LA dimer was identified as the main species at even higher concentration in CDCl3. The present work showcases the power of MI-VCD spectroscopy in aiding solution spectral assignment and in providing insight into the complex self-aggregation behavior of LA in solution.
- This article is part of the themed collection: Challenges in spectroscopy: accuracy vs interpretation from isolated molecules to condensed phases


 Please wait while we load your content...
Please wait while we load your content...