Rovibrational quantum dynamics of the vinyl radical and its deuterated isotopologues
Abstract
Rotational–vibrational states up to 3200 cm−1, beyond the highest-lying stretching fundamental, are computed variationally for the vinyl radical (VR), H2Cβ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CαH, and the following deuterated isotopologues of VR: CH2
CαH, and the following deuterated isotopologues of VR: CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CD, CHD
CD, CHD![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH, and CD2
CH, and CD2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CD. The height of the CαH tunneling rocking barrier of VR, partially responsible for the complex nuclear dynamics of VR and its isotopologues, is determined to be 1641 ± 25 cm−1 by the focal-point analysis approach. The definitive nuclear-motion computations performed utilize two previously published potential energy hypersurfaces and reveal interesting energy-level and tunneling patterns characterizing the internal motions of the four isotopologues. A full assignment, including symmetry labels, of the vibrational states computed for CH2
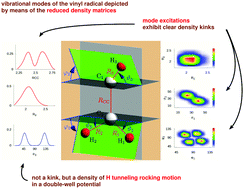
CD. The height of the CαH tunneling rocking barrier of VR, partially responsible for the complex nuclear dynamics of VR and its isotopologues, is determined to be 1641 ± 25 cm−1 by the focal-point analysis approach. The definitive nuclear-motion computations performed utilize two previously published potential energy hypersurfaces and reveal interesting energy-level and tunneling patterns characterizing the internal motions of the four isotopologues. A full assignment, including symmetry labels, of the vibrational states computed for CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH is provided, whenever feasible, based on the analysis of wave functions and the related one- and two-mode reduced density matrices. The computed vibrational states of CH2
CH is provided, whenever feasible, based on the analysis of wave functions and the related one- and two-mode reduced density matrices. The computed vibrational states of CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CD and CD2
CD and CD2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CD are characterized up to slightly above the top of the barrier. Interestingly, it is the interplay of the ν6 (formally CH2 rock) and ν7 (formally CH rock) modes that determines the tunneling dynamics; thus, the description of tunneling in VR needs, as a minimum, the consideration of two in-plane bending motions at the two ends of the molecule. When feasible, the computed results are compared to their experimental counterparts as well as to previous computational results. Corrections to the placement of the ν4 and ν6 fundamentals of VR are proposed. Tunneling switching, a unique phenomenon characterizing tunneling in slightly asymmetric effective double-well potentials, is observed and discussed for CHD
CD are characterized up to slightly above the top of the barrier. Interestingly, it is the interplay of the ν6 (formally CH2 rock) and ν7 (formally CH rock) modes that determines the tunneling dynamics; thus, the description of tunneling in VR needs, as a minimum, the consideration of two in-plane bending motions at the two ends of the molecule. When feasible, the computed results are compared to their experimental counterparts as well as to previous computational results. Corrections to the placement of the ν4 and ν6 fundamentals of VR are proposed. Tunneling switching, a unique phenomenon characterizing tunneling in slightly asymmetric effective double-well potentials, is observed and discussed for CHD![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH. Despite the extensive tunneling dynamics, the rotational energy-level structure of VR exhibits rigid-rotor-type behavior.
CH. Despite the extensive tunneling dynamics, the rotational energy-level structure of VR exhibits rigid-rotor-type behavior.
- This article is part of the themed collections: Challenges in spectroscopy: accuracy vs interpretation from isolated molecules to condensed phases and 2018 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...