Double resonance rotational spectroscopy of He–HCO+
Abstract
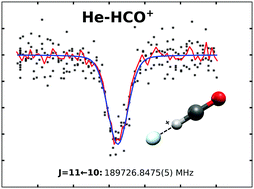
The ground state of He–HCO+ is investigated using a recently developed double resonance technique, consisting of a rotational transition followed by a vibrational transition into a dissociative state. In order to derive precise predictions for the rotational states, the high resolution infrared predissociation spectroscopy of the v1 C–H stretching mode is revisited. Eleven pure rotational transitions are measured via the double resonance method. A least squares fit of these transitions to a standard linear rotor Hamiltonian reveals that the semirigid rotor model cannot fully describe the loosely bound He–HCO+ complex. The novel double resonance technique is compared with other action spectroscopic schemes, and some potential future applications are presented.
- This article is part of the themed collections: Challenges in spectroscopy: accuracy vs interpretation from isolated molecules to condensed phases and 2018 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...