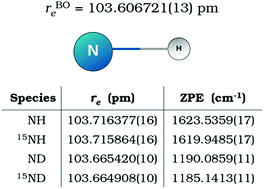
The rotational spectrum of 15ND in its ground electronic X3Σ− state has been observed for the first time. Forty-three hyperfine-structure components belonging to the ground and ν = 1 vibrational states have been recorded with a frequency-modulation millimeter-/submillimeter-wave spectrometer. These new measurements, together with the ones available for the other isotopologues NH, ND, and 15NH, have been simultaneously analysed using the Dunham model to represent the ro-vibrational, fine, and hyperfine energy contributions. The least-squares fit of more than 1500 transitions yielded an extensive set of isotopically independent Ulm parameters plus 13 Born–Oppenheimer Breakdown coefficients Δlm. As an alternative approach, we performed a Dunham analysis in terms of the most abundant isotopologue coefficients Ylm and some isotopically dependent Born–Oppenheimer Breakdown constants δlm [R. J. Le Roy, J. Mol. Spectrosc., 1999, 194, 189]. The two fits provide results of equivalent quality. The Born–Oppenheimer equilibrium bond distance for the imidogen radical has been calculated [rBOe = 103.606721(13) pm] and zero-point energies have been derived for all the isotopologues.