Quantum tunneling dynamical behaviour on weakly bound complexes: the case of a CO2–N2 dimer†
Abstract
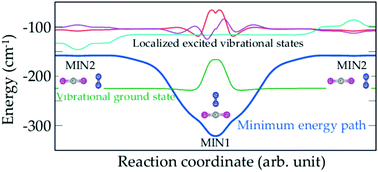
Quantum tunneling is a common fundamental quantum mechanical phenomenon. The dynamics induced by this effect is closely connected to the shape of the potentials. Here we treat the CO2–N2 van der Waals complex dynamics using a first principles treatment where nuclear motions and nuclear spins are fully considered. This dimer is found to exhibit complex spectral and dynamical features that cannot be accounted for using standard experimental and theoretical models. We shed light on some aspects of its quantum tunneling dynamics that remained unexplained since its first evidence 85 years ago. CO2–N2 represents also an important prototype for studying the systematic (as in NH3) lifting of degeneracy due to tunneling effects and large amplitude motions. Vibrational memory and quantum localization effects are evidenced. Plural potential wells separated by potential barriers are commonly found for polyatomic organic and inorganic molecules (e.g., cis–trans isomerization and enol–keto tautomerism). The present findings are useful for understanding the complex quantum effects that may occur there.
- This article is part of the themed collection: Challenges in spectroscopy: accuracy vs interpretation from isolated molecules to condensed phases


 Please wait while we load your content...
Please wait while we load your content...