Interactions between azines and alcohols: a rotational study of pyridine–tert-butyl alcohol
Abstract
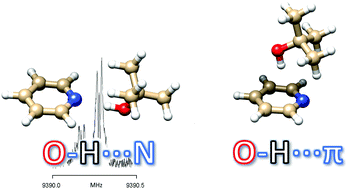
We assigned the rotational spectra of the parent and the OD isotopologues of the intermolecular complex pyridine–tert-butyl alcohol. The rotational and 14N quadrupole coupling constants are in agreement with a σ-type shape and a Cs symmetry of the complex. The two subunits are held together by a “classical” O–H⋯N intermolecular hydrogen bond. Structural features of these hydrogen bonds are given and compared to those of similar molecular adducts. The O⋯N distance decreases by 4 mÅ upon deuteration of the hydroxyl group, denoting a marked reverse Ubbelohde effect of the O–H⋯N hydrogen bond.
- This article is part of the themed collection: Challenges in spectroscopy: accuracy vs interpretation from isolated molecules to condensed phases


 Please wait while we load your content...
Please wait while we load your content...