A combined experimental and theoretical study of optical rotatory dispersion for (R)-glycidyl methyl ether in aqueous solution†
Abstract
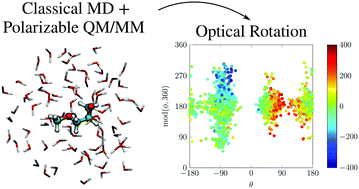
The dispersive optical activity for aqueous solutions of non-rigid (R)-glycidyl methyl ether (R-GME) has been explored synergistically from experimental and theoretical perspectives. Density functional theory analyses performed with the polarizable continuum model for implicit solvation identified nine low-lying stable conformers that are interconverted by rotation about two large-amplitude torsional coordinates. The antagonistic chiroptical signatures predicted for these structural isomers were averaged under a Boltzmann-weighting ansatz to estimate the behavior expected for a thermally equilibrated ensemble. This led to optical rotatory dispersion profiles that reproduced the overall shape of observations but failed to achieve uniform agreement with measured specific-rotation values even when anharmonic vibrational corrections were applied. A mixed QM/FQ paradigm, whereby quantum-mechanical (QM) calculations of optical activity were combined with classical molecular dynamics simulations of explicit solvation that included mutual-polarization effects by means of fluctuating charges (FQ), was enlisted to elucidate the microsolvation environment and gauge its impact upon conformer distributions and response properties. Although quantitative accord with experiments remained elusive, this approach revealed strong variations in the magnitude and sign of rotatory powers for R-GME as the configuration of surrounding water molecules evolved, thereby highlighting the inherently dynamical nature of the solvated chiroptical response, calling into question the validity of “static” descriptions based on the presumption of distinct energy minima, and giving insight into the inherent complexity posed by the modeling of such properties for solvated systems.
- This article is part of the themed collection: Challenges in spectroscopy: accuracy vs interpretation from isolated molecules to condensed phases


 Please wait while we load your content...
Please wait while we load your content...
