Photodissociation of CH2BrI using cavity ring-down spectroscopy: in search of a BrI elimination channel†
Abstract
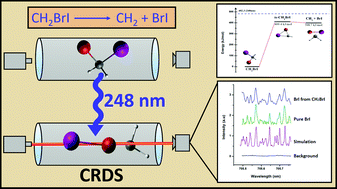
Photodissociation of CH2BrI was investigated in search of unimolecular elimination of BrI via a primary channel using cavity ring-down absorption spectroscopy (CRDS) at 248 nm. The BrI spectra were acquired involving the first three ground vibrational levels corresponding to A3Π1 ← X1Σ+ transition. With the aid of spectral simulation, the BrI rotational lines were assigned. The nascent vibrational populations for v′′ = 0, 1, and 2 levels are obtained with a population ratio of 1 : (0.58 ± 0.10) : (0.34 ± 0.05), corresponding to a Boltzmann-like vibrational temperature of 713 ± 49 K. The quantum yield of the ground state BrI elimination reaction is determined to be 0.044 ± 0.014. The CCSD(T)//B3LYP/MIDI! method was employed to explore the potential energy surface for the unimolecular elimination of BrI from CH2BrI.
- This article is part of the themed collections: Photodissociation and reaction dynamics and 2018 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...