Spectroscopy of a rotating hydrogen molecule in carbon nanotubes†
Abstract
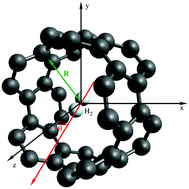
A first-principles study of the spectroscopy of a single hydrogen molecule rotating inside and outside of carbon nanotubes is presented. Density functional theory (DFT)-based symmetry-adapted perturbation theory (SAPT) is applied to analyze the influence of the rotation in the dispersionless and dispersion energy contributions to the adsorbate–nanotube interaction. A potential model for the H2–nanotube interaction is proposed and applied to derive the molecular energy levels of the rotating hydrogen molecule. The SAPT-based analysis shows that a subtle balance between the dispersionless and dispersion contributions is key in determining the angular dependence of the H2–nanotube interaction, which is strongly influenced by the diameter of the carbon nanotubes. As a consequence, the structure of molecular energy levels is very different in wide and narrow nanotubes with the diameter above and below 1 nanometer, respectively. Strong anisotropy effects lead to a rather constrained rotation of molecular hydrogen inside narrow nanotubes.
- This article is part of the themed collections: Challenges in spectroscopy: accuracy vs interpretation from isolated molecules to condensed phases and 2018 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...