Pd doping, conformational, and charge effects on the dichroic response of a monolayer protected Au38(SR)24 nanocluster†
Abstract
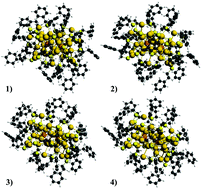
TDDFT simulations of the absorption and CD spectra of a Pd2Au36(SC2H4Ph)24 monolayer-protected cluster (MPC) are carried out with the aim of investigating the effects of doping, conformational degrees of freedom of the thiolates’ end-groups, and charge states on the optical and dichroic response of a prototypical MPC species. Clear signatures of Pd doping in both absorption and CD spectra are found to be a consequence of the participation of Pd (4d) states in the ligand-based d-band and on the unoccupied MOs of lower energy. Exploration of conformational space points to a much greater sensitivity of optical rotation to the conformation of the end-groups of the organic monolayer compared to absorption. Finally, the effect of charge is mainly seen as a decreased dependence of the dichroic response on conformation. The agreement between the TDDFT predictions and the available experimental data is good, and enables an assignment of absorption and CD bands to specific classes of one-particle excitations.
- This article is part of the themed collection: Challenges in spectroscopy: accuracy vs interpretation from isolated molecules to condensed phases


 Please wait while we load your content...
Please wait while we load your content...