On the simulation of vibrationally resolved electronic spectra of medium-size molecules: the case of styryl substituted BODIPYs†
Abstract
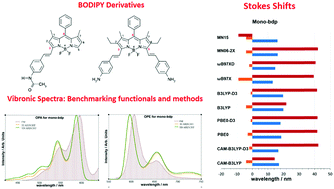
BODIPY dyes are used in a variety of applications because of their peculiar spectroscopic and photo-physical properties that vary depending on the stereochemistry of the functional groups attached to the boron-dipyrromethene core structure. In this work, we have applied several computational methods, adapted for semi-rigid molecules based on the Franck–Condon principle, for the study of the optical properties of BODIPY systems and for the understanding of the influence of functional groups on their spectroscopic features. We have analyzed the electronic spectra of two styryl substituted BODIPY molecules of technological interest, properly taking into account the vibronic contribution. For comparison with recently recorded experimental data in methanol, the vibrationally resolved electronic spectra of these systems were computed using both Time-Independent (TI) and Time-Dependent (TD) formalisms. The first step toward the analysis of optical properties of the styryl modified BODIPYs was a benchmark of several density functionals, to select the most appropriate one. We have found that all benchmarked functionals provide good results in terms of band shape but some of them show strong discrepancies in terms of band position. Beyond the issue of the electronic structure calculation method, different levels of sophistication can be adopted for the calculation of vibronic transitions. In this study, the effect of mode couplings and the influence of the Herzberg–Teller terms on the theoretical spectra has been investigated. It has been found that all levels of theory considered give reproducible results for the investigated systems: band positions and shapes are similar at all levels and little improvements have been found in terms of band shape with the inclusion of Herzberg–Teller effect. Inclusion of temperature effects proved to be challenging due to the important impact of large amplitude motions. Better agreement can be achieved by adopting a suitable set of coordinates coupled with a reduced-dimensionality scheme.
- This article is part of the themed collection: Challenges in spectroscopy: accuracy vs interpretation from isolated molecules to condensed phases


 Please wait while we load your content...
Please wait while we load your content...