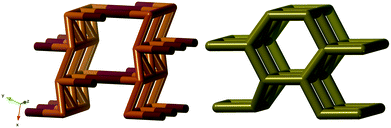Natural and synthetic metal oxalates – a topology approach

Abstract

Oxalates are found in minerals and in biology, are made in the laboratory, and are used on an industrial scale. They form coordination polymers and hydrogen bonded networks that often can be analysed using network topology. In this survey of known naturally occurring oxalates we note weddellite, [Ca(C₂O₄)]·xH₂O, that seems to be the first known naturally occurring metal–organic framework, forming the four-connected crb-net (zeolite CRB). The natural oxalates are typically 3D, 2D or 1D coordination polymers, with extensive hydrogen bonding in the latter cases. For example, humboldtine and lindbergite form the new 3- and 8-connected net hum by combining the 1D structure with strong hydrogen bonds. Tris-oxalates rarely occur in nature but stepanovite, [Mg(H₂O)₆][Na[Fe(ox)₃]]·3H₂O, is an exception and forms hcb-nets (honeycomb 2D layers) with the hexaaqua ions sealing any potential voids. Synthetic tris-oxalates on the other hand are well explored and normally form 2D hcb-nets or 3D chiral three-connected srs-nets. Theoretically a few other topologies should also be possible, and it was found that [Mn((R)-salmen)(CH₃OH)(CH₃CN)][MnCr(ox)₃]·0.5CH₃OH·1.25CH₃CN forms the achiral three-connected lig-net, [Fe(2,6-bis(pyrazol-3-yl)pyridine)₂][MnCr(ox)₃]·2,6-bis(pyrazol-3-yl)pyridine·CH₃OH forms the likewise achiral nod-net and [Cu(trans[14]dien)][KCr(ox)₃] the ths-net. A new binodal 3-connected net noa (with the derived 3c-,4c- new net mys) was found in [Fe^II(tren(imid)₃)]₂[Mn_2.5(CH₃OH)₃Cr₃(ox)₉]·(CH₃OH)_4.75·(H₂O)₄. The more complex [Fe(tren(imid)₃)]₂[Mn_2.5(CH₃OH)₃Cr₃(ox)₉] forms a new three-nodal 3-connected daz-net.

---

1. Introduction

Oxalic acid and oxalates date far back in human history, both found as a tasty part of numerous plants, and in painful and dangerous kidney and bladder stones. In industry, they are used in the separation of various metals, and other practical examples employing the ubiquitous C₂O₄²⁻ unit are in artistic chemical photography processes and the anticancer drug oxaliplatin (trade name Eloxatin).¹ But oxalates are also very much present in today's cutting edge science.^2–7 Recently, for example, MOFs from tetrakis oxalates with zeolite topologies have been prepared.³

Tri-potassium trioxalato-rhodium monohydrate was the focus of the first diffraction study of oxalates in 1927 (ZZZVZK)⁸ followed by beryllium oxalate trihydrate in 1928 (ZZZQZK), and today the Cambridge Crystallographic Data Centre has collected over 6000 oxalate entries into the CSD.

Due to the possibility of the oxalate ion forming bridging chelates in two or more directions, and its many hydrogen bond accepting sites, oxalate compounds often form networks. The topological analysis of such networks has its origins in the work of Alexander Wells starting in the 1950s,^9,10 gaining popularity by the analysis of coordination polymers and metal–organic frameworks (MOFs) in the 1990s and onwards.^11–13

Here, we report how well metal compounds with small oxalate ions (ox) lend themselves to such topological analysis. We will show the importance of network topologies in both the synthesis of new oxalate compounds and in the communication and understanding of known oxalates, both natural and synthetic.¹⁴

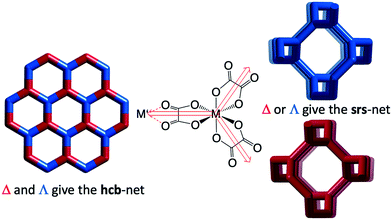
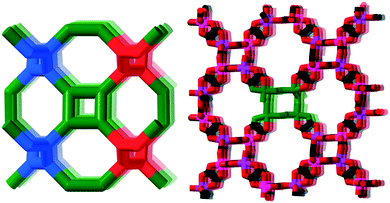
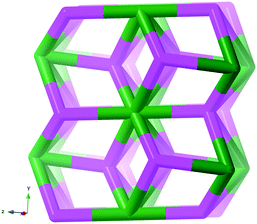
We have investigated two cases, first the tris-oxalates, [M′M(ox)₃], forming three-connected networks. These are known to produce 2D hcb-nets (honeycomb nets, Fig. 1 left) or the 3D chiral srs-nets (or (10,3)-a, Fig. 1 right), but geometrical considerations suggest that also a number of other 3-connected topologies should be conceivable, even though the srs-net appears to be the perfect fit for enantiomerically pure tris-oxalates.^13,15

Fig. 1 Tris-oxalates, [M′M(ox)₃], form three-connected networks. These are known to produce 3D chiral srs-nets (right) with only one enantiomer and 2D hcb-nets (left) when both enantiomers are present.

We do not consider the four-connecting tetrakis-oxalates here if they are not naturally occurring, as these have been discussed elsewhere.^3,16

Secondly, we consider the natural oxalates, recently reviewed by Piro and Baran.¹⁷ Through the 2D tris-oxalate hcb-nets there is some overlap with the first group,¹⁸ and the rare Siberian mineral stepanovite had its 15 minutes of fame a few years ago^19,20 when the structures were, unexpectedly, found to resemble “well-established magnetic and proton-conducting metal oxalate MOFs”.²¹

2. Experimental

2.1 Materials and methods

2.1.1 Searching the Cambridge Structural Database (CSD). The CSD 5.40 (September 2019) was used. In all runs the Conquest software (version 2.0.2 or 2.0.3) was used. To compute bridging tris-oxalates, an [M₃[M(ox)₃]] entity was used as a query, and to exclude the tetrakis-oxalates and only include extended networks, the central M was restricted to a maximum of 7 bonding atoms and at least one M–O bond was specified as polymeric.

2.1.2 Computational details. The network topologies discussed in this article were obtained using the freeware programs ToposPro²² and Systre²³ operating on the original crystallographic information files for the compounds in question, or on files derived from these. Throughout we discuss the topologies using three-letter symbols in the web-based and free Reticular Chemistry Structural Resource database, RCSR,²⁴ as encouraged by IUPAC.²⁵

3. Results and discussion

3.1 Tris-oxalates, [M′M(ox)₃]^x−

The Cambridge Structural Database in total contains 682 entries with a minimum of three bridging oxalates (15 added to the latest 5.40 tri-annual update), and at least 301 of these are tris-oxalate networks either with M = M′ or with different M and M′. A recent survey of srs-nets (Fig. 1) lists 91 tris-oxalates having the srs-network topology,²⁶ and as not all of the remaining ones form the 2D hcb-net (Fig. 1), we wondered about these network topologies. Is there one particular topology that is the second “choice” or are there many possibilities? And are they all chiral as the srs-net?

In Table 1, we have collected the tris-oxalates from the CSD that form neither the srs nor hcb-net.

Table 1 Tris-oxalates [M′M(ox)₃]^x− from the CSD that form neither the srs nor hcb-net

M′M	Cation	CSD	Net
a Severely disordered. b New topologies.
Mn(II) Cr(III)	[Mn((S)-salmen)(CH3OH)2]^+	BEWVEG	lig
Mn(II) Cr(III)	[Mn((R)-salmen)(CH3OH)2]^+	BEWVOQ	lig
Mn(II) Cr(III)	[Fe(imid2-trien)]^2+	VINHOR	lig
Mn(II) Cr(III)	[Fe(tren(6-Me-py)3)]^2+	VINHIL	lig
Mn(II) Cr(III)	[Fe(2,6-bis(pyrazol-3-yl)pyridine)2]^2+^a	EDATOT	nod
Mn(II) Cr(III)	[Fe(sal2-trien)]^3+	GURPIT	nod
Mn(II) Cr(III)	[In(sal2-trien)]^3+	GURPOZ	nod
Mn(II) Cr(III)	[In(sal2-trien)]^3+	GURPUF	nod
Mn(II) Cr(III)	[Fe(5-CH3Osal2-trien)]^3+	PUWZOX	nod
Mn(II) Cr(III)	[Mn(salen)(H2O)]2^2+	PIQFIG	nod
Mn(II) Cr(III)	(H2PPD^+)(benzo[18]crown-6)2	RUGKEL	nod
K(I) Cr(III)	[Cu(trans[14]dien)]^2+	QIYXIF	ths
Cu(II)	HN(Et)2(CH2CH2OH)^+	KIRFIA	ths
Cu(II)	HN(Et)3^+	KEDJAG	ths
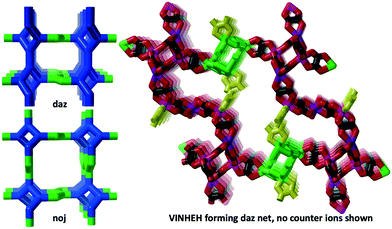
Mn(II) Cr(III)	[Fe(tren(imid)3)]2^2+	VINHEH	daz
Mn(II) Cr(III)	(o-FAni^+)2(DCH[18]crown-6)2	RUGKIP	noa

---

3.1.1 The lig-net. The lig-net (from LiGe, a Zintl phase with a three-connected Ge network) was identified by Blatov et al. in the coordination polymer [CdCl(tpht)(PPh₃Bz)], YINPEQ, where it is doubly interpenetrated.¹² It was also briefly discussed as a rod-packing by Rosi et al.²⁷ We found it in the metal-oxalate network in BEWVEG, [Mn((S)-salmen)(CH₃OH)₂][MnCr(ox)₃](CH₂Cl₂)_0.375(CH₃OH)_0.375 (H₂O)_0.125,²⁸ see Fig. 2.

Fig. 2 Left: The ideal lig-net. Right: The metal-oxalate network in BEWVEG, [Mn((S)-salmen)(CH₃OH)₂][MnCr(ox)₃](CH₂Cl₂)_0.375(CH₃OH)_0.375(H₂O)_0.125, forming the lig-net. Note the opposite chirality of the helices (coloured blue and red, left).

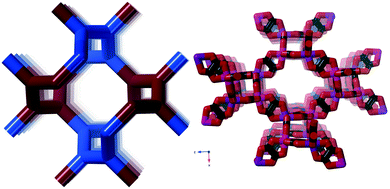
Compared to the nets discussed by Öhrström & Larsson that were all formed from 10-gons as the shortest rings between nodes, the lig-net also forms 8-rings (point symbol 8²10 and vertex symbol 8·8·10₃ (ref.15)). This and other three-connected nets are discussed in detail in ref. 13.

3.1.2 The nod-net. The nod-net also forms 8-rings, but is a binodal net with the point symbol²⁹ 8²10·8²10 and the vertex symbol²⁹ 8·8·10₃ 8·8·10₃. The metal-oxalate network in GURPIT, [Fe(sal₂-trien)][MnCr(ox)₃]·CH₃OH,³⁰ forms the nod-net, see Fig. 3.

Fig. 3 Left: The ideal nod-net. Right: The metal-oxalate network in GURPIT, [Fe(sal₂-trien)][MnCr(ox)₃]·CH₃OH, forming the nod-net. Note the opposite chirality of the helices (coloured blue and red, left).

3.1.3 The ths-net. The ths-net (from ThSi₂, also known as the 10,3-b net) is similar to the srs-net as it is also a 10,3-net, meaning that all the shortest rings are 10-gons. Its point symbol is 10³ just as the srs, but the vertex symbols differ; 10₅·10₅·10₅ for srsversus 10₂·10₄·10₄ for ths (meaning that the number of different 10-gons forming the shortest circuits differ). A further difference is that ths is achiral and does not have the characteristic four-fold helices of srs, lig, nod, and some other 3-connected nets.

We found this net in for example [Cu(trans[14]dien)][KCr(ox)₃],³¹ where trans[14]dien is 5,7,7,12,14,14-hexamethyl-1,4,8,11-tetraazacyclotetradeca-4,11-diene. In Fig. 4, it is shown (right) together with the ideal version of the ths-net (left).

Fig. 4 Left: The ideal ths-net. Right: The metal-oxalate network in QIYXIF, [Cu(trans[14]dien)][KCr(ox)₃] forming the achiral ths-net.

3.1.4 The noa-net. While the preceding nets have all been described and found in various compounds (occurrence can be checked with ToposPro) we were surprised to find a new two-nodal three-connected net noa in RUGKIP (o-FAni⁺)₂(DCH[18]crown-6)₂[Mn(CH₃OH) Cr(oxalate)₃][MnCr(oxalate)₃](CH₃OH).³² This new net has point symbols 4·8·10 and 8·10² and again we see the characteristic four-fold helices in a racemic set-up, but this time connected by four rings. This enforces 90° angles in the network, and this is achieved by one of the Mn ions having one mono-coordinated oxalate ion and a methanol molecule completing the octahedron. The ideal net and the network in RUGKIP are presented in Fig. 5.

Fig. 5 Left: The ideal noa-net. Right: The metal-oxalate network in RUGKIP, (o-FAni⁺)₂(DCH[18]crown-6)₂[Mn(CH₃OH)Cr(oxalate)₃][MnCr(oxalate)₃](CH₃OH) forming the achiral noa-net. The square planar connections are coloured green in both pictures.

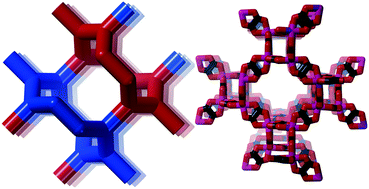
It has not escaped us that the noa-net is an augmented form of a three- and four-connected net with the four connected nodes in the centre of the squares. Somewhat surprisingly this is not the known jph-net¹⁶ but yet another new topology, mys, with point symbols 6·8² and 6²·8²·10². They differ again, just as lig and nod, in the arrangement of the four-fold helices of opposite chirality, see ESI† Fig. S1.

3.1.5 The daz-net. To finish off this section we want to comment on a more complicated structure. [Fe^II(tren(imid)₃)]₂[Mn_2.5(CH₃OH)₃Cr₃(ox)₉]·(CH₃OH)_4.75·(H₂O)₄³³ has both bridging and terminal oxalates, as well as a bis oxalate entity with terminating methanol ligands. This gives a total of six symmetry independent coordination entities in the structure, but only three of these are nodes in the network shown in Fig. 6.

Fig. 6 Left: The ideal tri-nodal daz-net and the related noj-net. Chirality colour coded as before, in green colour are the non-chiral zigzag connectors. Right: The metal-oxalate network in VINHEH, [Fe(tren(imid)₃)]₂[MnCr(ox)₃], forming the daz-net. Terminating oxalates colour coded yellow and the helices corresponding to the zigzag connection in green just as in the ideal net (left). The noj-net is found in XEHXOX.

The resulting network topology is tri-nodal and chiral, but would be of limited interest to the crystal engineering community if it was not for its clear relationship to the nets already discussed and to other similar nets in the RCSR. The point symbols are 8³, 8³, and 8·10² and the Topos topological type is 3,3,3 T12.

As can be seen in Fig. 6 (left), the ideal daz-net resembles the srs-net, only with a zigzag motif added between helices along the z-axis. It is also related to the likewise chiral binodal noj-net that essentially is an srs-net with the zigzag motif inserted between all helices.

It is currently not known if there are similar versions of the achiral lig and nod nets.

We note, however, that the analysis of the structure using the daz-net greatly simplifies the task and renders “a very irregular 3D oxalate network”³³ into a reasonably understandable geometrical object.

3.1.6 Geometrical requirements of the nets. Topology is invariant to bending, squeezing and twisting as long as no bonds are broken. Many nets can be adjusted so that the dihedral angles between nodes more or less match what is needed between two tris-oxalate complexes. A detailed analysis of some of these geometries is found in ref. 15. Here, in Table 2, we note the ideal densities (as the number of vertices per unit volume) of these nets.

Table 2 Densities, as the number of vertices per unit volume, of some selected, ideal, nets. Data from the RCSR

Net	Alt. name	Point symbol	Density^a
a Number of vertices per unit volume.
srs	10,3-a	10^3	0.3536
lig	8^210-a	8^2·10; 8^2·10	0.3536
nod	8^210-b	8^2·10; 8^2·10	0.3535
bto	10,3-c	10^3	0.5132
ths	10,3-b	10^3	0.4218
utp	10,3-d	10^3	0.4218
noj	8,3-d	8^3; 8^3	0.3241

---

From this point of view it can be noted that the srs-net has a very good fit to the oxalate networks, (see ref. 13 and 15 for details) and counter ions like [M(1,10-bipyridine)₃]ⁿ⁺ fit nicely inside. It is therefore not surprising that nets with similar densities like nod and lig form with cations of similar size.

3.1.7 Rationale for topology choice of the system. In the studies surveyed, there has been no single reason pointed out responsible for which network topology any system will adopt. Unfortunately, we cannot point out a single factor either. The following discussion is a summary and a few comments on the rationales given in each individual paper. For clarity, Lewis structures and space filling models of the individual cations are presented in Fig. S2.†

BEWVEG and BEWVOQ are typical examples. The authors demonstrated that using the same cation, [Mn(R)-salmen]⁺ or [Mn(S)-salmen]⁺, the 3D oxalate network depends on the choice of solvent.²⁸ When crystallized in acetonitrile, a 2D hcb-net resulted (BEWVIK and BEWVUW) instead of the 3D lig-net obtained from dichloromethane. Pertinent differences between the two structures are the configuration of the two phenoxy arms and the presence of different solvent molecules coordinated to Mn^III in the two apical positions of the structure, [Mn(R/S)-salmen(CH₃OH)₂]⁺ for lig, whereas the hcb ones contain [Mn(R/S)-salmen(CH₃CN)₂]⁺ together with [Mn(R/S)-salmen(CH₃OH)₂]⁺.

VINHOR and VINHIL³³ on the other hand, both lig-nets, get their network from the heptacoordinated Mn^II ions in each structure. The difference between these structures is that in VINHOR all the Mn atoms are heptacoordinated, and in VINHIL the second crystallographically independent Mn atom is hexacoordinated with a strong trigonal distortion of its octahedral coordination, which give rise to the presence of O–Mn–O angles of 154.6° instead of 180° expected for an octahedral coordination. The methanol in these two complexes is attached to the trioxalate network. Another remark on these two compounds is that the smaller number of cations necessary (+2 vs. +1 in i.e. BEWVEG) to compensate the negative charge of the oxalate network produces a more irregular network with heptacoordinated Mn^II ions coordinated to solvent molecules, and a more open structure with pores filled with disordered solvent molecules.

The nod-net in EDATOT³⁴ may be related to a solvent effect. There is a presence of many interstitial solvent molecules since only one Fe complex is present per Mn/Cr pair, and results in no extra anions needed to stabilize the complex. The lower occupancy of cations and anions inside the anionic network could be the main cause for losing the enantiopure character of these systems.

Combining [Fe^III(5-Xsal₂-trien)]⁺ (X = NO₂ or CH₃O) with the Mn^IICr^III oxalates resulted in two different networks.³⁵ The cation [Fe^III(5-NO₂sal₂-trien)] gave a 2D hcb-net (PUWZIZ) since the electron withdrawing group favors π⋯π stacking interactions between phenyl rings of neighboring cationic complexes. In contrast, in PUWZOX the phenyls are not face to face. This is explained by the presence of the methoxy groups that hinders the face to face orientation of the neighboring rings. The dihedral angles, α, between the least-squares planes of the two phenoxy rings of the hcb-net are α = 89.002° ([Fe1] complex) and α = 94.248° ([Fe2] complex) and the dihedral angles, α, between the phenoxy rings in PUWZOX forming the nod-net are for [Fe1A], [Fe1B] and [Fe2] 110.47, 100.41 and 105.55°, respectively. The dihedral angles, α, between the least-squares planes of the two phenoxy rings have very different values in the 2D or 3D structures. Thus, the two phenoxy rings in the 2D compound (PUWZIZ) are closer to 90°, the ideal value for an octahedral complex.

3.1.8 The absence of interpenetration for these systems. The intergrowth of two or more networks is a common feature for coordination polymers,^12,13 and for the srs-net in particular many examples exist, see for instance ref. 41. However, in the tris-oxalate systems the srs-net is always negatively charged and two such nets interpenetrated in the same compound would require doubling the number of cations while at the same time leaving much less space for them. We believe that these two requirements are difficult to fulfil and therefore interpenetration is not observed in this class of compounds.

3.2 Naturally occurring metal oxalates

Metal oxalates from minerals come in a large variety, from the class of tris-oxalates we have seen in the preceding section, to more or less discrete molecular entities held together by hydrogen bonds. While the former are normally straightforward to analyse, hydrogen bonded systems may be more ambiguous, and even simple metal oxalates may use multiple bonding sites on the oxalates, making some of these systems equally challenging.³⁶

In Table 3, we have assembled naturally occurring oxalates according to Piro and Baran¹⁷ with the network analysis performed by our group. We have mainly concentrated on the 3D and 2D coordination polymers, but the very simple humboldtine and lindbergite, the Fe and Mn versions of two isostructural 1D [M(C₂O₄)(H₂O)₂] oxalates, have also been included. In this latter case, the coordination network is supplemented with strong hydrogen bonds between coordinated water and oxalate ions.

Table 3 Naturally occurring metal-oxalates according to Piro and Baran, and their networks

Compound	Formula	Net	Node^a
a ox = oxalate centroid. b New topology.
3D coordination networks
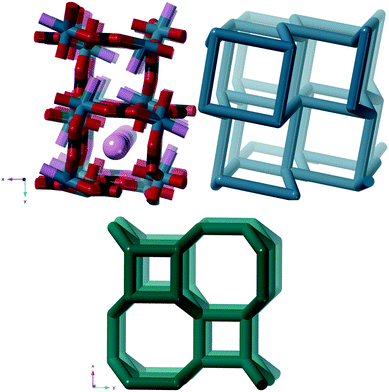
Weddellite	[Ca(C2O4)(H2O)2]·xH2O	crb	Ca
Natroxalate	[Na2(C2O4)]	fit	Na, ox
Wheatleyite	[Na2[Cu(C2O4)2](H2O)2]	sxd	Na
Whewellite	[Ca(C2O4)H2O]	sqp	Ca
Novgorodavaite	[Ca2Cl2(C2O4)(H2O)2]	sqp	Ca
2D coordination networks
Zhemchuzhnikovite	[Mg(H2O)6][AlNa(C2O4)3]·2H2O	hcb	Mg, Al
Stepanovite	[Mg(H2O)6][FeNa(C2O4)3]·3H2O	hcb	Mg, Fe
Deveroite	[Ce2(C2O4)3(H2O)6]·4H2O	hcb	Ce
Coskrenite	[Ce2(C2O4)(SO4)2(H2O)8]	hxl	Ce
1D coordination networks or polymers
Humboldtine	[Fe(C2O4)(H2O)2]	hum	Fe, H2O
Lindbergite	[Mn(C2O4)(H2O)2]	hum	Mn, H2O
Levinsonite	[Al(H2O)6][Y(C2O4)(SO4)2(H2O)3]·3H2O		—
Zugshunstite	[Al(H2O)6][Ce(C2O4)(SO4)2(H2O)3]·3H2O		—

---

3.2.1 Stepanovite and zhemchuzhnikovite. While stepanovite (OKUTUL03) [Mg(H₂O)₆][FeNa(C₂O₄)₃]·3H₂O and zhemchuzhnikovite (OKUVAT02) [Mg(H₂O)₆][AlNa(C₂O₄)₃]·2H₂O form the 2D hcb-net in very attractive structures, the hydrated metal ions ([Mg(H₂O)₆]²⁺) that completely fill the voids indicate that these are not real MOFs. The IUPAC definition states that a MOF should be “potentially porous”,²⁵ and as the cations fill the perceived channels, it does not fit the bill. Nevertheless, forming a network of metal carboxylates does make them MOF-like in some aspects.

3.2.2 Weddellite. Weddellite (also “weddelite”), on the other hand, has been reported to lose water without a change in morphology³⁷ and is thus a potential candidate for a “natural” MOF. This compound, with a square antiprismatic calcium ion coordinating three oxalate ions and two water molecules, has the approximate formula [Ca(ox)(H₂O)₂]·xH₂O and the oxalates bridge the Ca²⁺ ions as depicted in Fig. 7.

Fig. 7 Weddellite, [Ca(C₂O₄)(H₂O)₂]·xH₂O, with a square antiprismatic calcium ion coordinating three oxalate ions and two water molecules forms a four-connected network as indicated by the blue-grey bold lines.

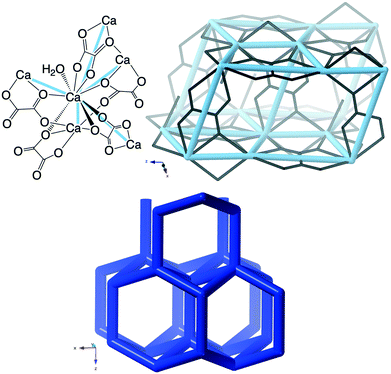
The crystal structure according to Tazzoli and Domeneghetti³⁸ (CSD code WHWLTB) is shown in Fig. 8 together with the crb-net formed.

Fig. 8 Top left: Crystal structure of weddellite, [Ca(C₂O₄)(H₂O)₂]·xH₂O, water in pink. Top right: The crb-net formed. This is the only known naturally occurring metal–organic framework. Bottom: The ideal crb-net.

The porosity of weddellite has not been rigorously proven. However, in a study using an environmental scanning electron microscope with a heating stage attached, no changes in the crystal morphology were observed as water was desorbed³⁷ and recently detailed variable temperature single crystal and powder X-ray diffraction (XRD) has confirmed structural integrity up to 105–140 °C after which the structure collapses.³⁹

3.2.3 Natroxalate. In the crystal structure of natroxalate, [Na₂(C₂O₄)] (CSD code NAOXAL – NAOXAL20), we no longer see distinct oxalate bridges, but rather a much more tightly packed system. In this compound every sodium ion binds to five oxalate ions, and every oxalate to ten sodium ions. The analysis is very straightforward, generating the 5 and 10 connected fit-net shown in Fig. 9.

Fig. 9 The 5 (Na⁺, pink) and 10 (oxalate centroids, green) connected fit-net in natroxalate, [Na₂(C₂O₄)]. This is a tightly packed structure without voids.

3.2.4 Wheatleyite. Wheatleyite is a mixed-metal mineral with formula [Na₂Cu(C₂O₄)₂]·2H₂O (CSD code CUOXNAII) composed of layers of sodium ions doubly bridged by oxygens from either oxalate or water that are connected through the [Cu(C₂O₄)₂]²⁻ bridge.

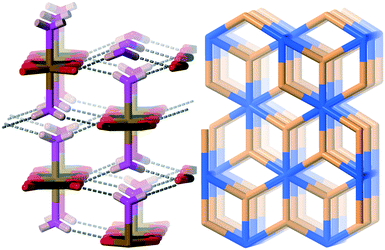
This forms the six-connected sxd-net and the network in the wheatleyite structure is shown in Fig. 10 together with the most symmetric form of the net.

Fig. 10 Left: The sxd-net in wheatleyite, [Na₂Cu(C₂O₄)₂]·2H₂O, orange is Na⁺ and mauve represents the [Cu(C₂O₄)₂]²⁻ bridge. Right: The ideal sxd-net.

3.2.5 Deveroite. Deveroite, [Ce₂(C₂O₄)₃(H₂O)₆]·4H₂O CSD code CEOXDH, also forms the 2D hcb-net despite Ce³⁺ being 9-coordinated. In contrast to stepanovite and zhemchuzhnikovite there are no counter ions that plug the empty space in the centre of the hexagons. However, the layers pack in an ABAB-fashion, with an offset, so that edges of layer A are in the middle of the hexagonal window of layer B, so no continuous open channels exist in this compound.

3.2.6 Whewellite. In whewellite, [Ca(C₂O₄)(H₂O)] CSD code CALOXM, as in weddellite, we find a square antiprismatic calcium ion with two bis-chelating oxalate ions. One water and oxygen atoms from three other oxalate ions complete the coordination sphere, making every calcium ion a five-connected node in an sqp-net, see Fig. 11.

Fig. 11 Top left: Whewellite, [Ca(C₂O₄)(H₂O)], with every Ca²⁺ five-connected node in an sqp-net. Top right: The sqp-net in whewellite. Below: The ideal sqp-net.

Inspecting this structure, one finds apparent voids, but they are all too small to be chemically significant.

3.2.7 Coskrenite. Coskrenite, [Ce₂(C₂O₄)(SO₄)₂(H₂O)₈], again forms a 2D network, a corrugated version of the six-connected hxl-net with lanthanoid ions (many possibilities exist) bridged by oxalates and sulfates. Structure data from entry 9004543 in the Crystallography Open Database.

3.2.8 Novgorodavaite. Novgorodavaite [Ca₂Cl₂(C₂O₄)(H₂O)₂] resembles whewellite in that it also forms a five-connected net with an sqp topology, see Fig. 12. Structure data from entry 0012496 in the American Mineralogist Crystal Structure Database.

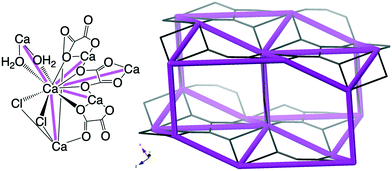Fig. 12 Top left: Novgorodavaite, [Ca₂Cl₂(C₂O₄)(H₂O)₂], with every Ca²⁺ five-connected node in an sqp-net. Top right: The sqp-net in novgorodavaite. The ideal sqp-net is shown in Fig. 11.

3.2.9 1D coordination polymers. The 1D coordination polymers are all straight chains with bis-chelating oxalates, M–oxalate–M. They all form hydrogen bonded networks, some more complex than others. Here, we consider only the isostructural humboldtine and lindbergite, the Fe and Mn versions of [M(C₂O₄)(H₂O)₂], respectively.

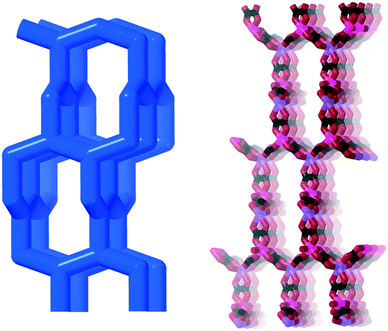
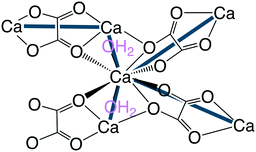
They have infinite bis-chelating –M–oxalate–M– chains with perpendicular coordinated water molecules, each hydrogen bonding to two oxalates. Taking the metal ions as one node and the water molecules as another, these structures form 3- and 8-connected nets. The water nodes are three-connected as they bind to the metal ion and then hydrogen bonds to two oxalates each. The metal ion node is eight connected as it binds to metal ions through coordination, two water molecules also via coordination, and then four waters via hydrogen bonds. This new topology hum is shown in Fig. 13 (right) together with the structure of humboldtine.

Fig. 13 The new 3- and 8-connected net hum (right) is formed from Fe and Mn (8-connect nodes) versions of [M(C₂O₄)(H₂O)₂] via 1D coordination polymers and hydrogen bonding between coordinated water (3-connect node) and oxalate (left).

4. Conclusions

Analysis of the CSD data indicates that synthetic 3D tris-oxalates occur in more than one network topology, even if the srs-net is by far the most common. The well-known nets nod, lig, and ths were found to occur, together with the new topologies noa and daz. It also suggests that, as different topologies have differently shaped and sized cavities, a rational approach to design compounds with other network topologies not encountered so far, should be possible.

Even so, the examples provided here give no clear guidance as how to perform such a rational design. Computational studies are in progress to address this question.

We also note that the issue may be more complex than a simple consideration of ideal geometries may suggest. Topologies stay the same even if bent, squeezed or otherwise distorted, as long as no bonds in the network are broken. Thus both the relative size and the shape of the empty space inside a particular network may be changed without changing the topology. Excellent examples are the “breathing” MOFs such as MIL-53.⁴⁰ Indeed we suggest that it should be possible to calculate a figure of merit for each network topology on the relative energetic cost of different distortions to further enhance their utility as blueprints for the design of molecule based materials.

We also note that the synthetic tris-oxalates are often multi component systems where the network can interplay with one or more guests.⁴¹ Taking the network topology into consideration will be one important step in making the synthesis of such materials a more rational process.

The natural oxalates present a more complex picture, and in Fig. 14 we have tried to summarize and contrast them to the more symmetric synthetic analogues. The new net hum was described as a model for the bonding and structure in humboldtine and lindbergite.

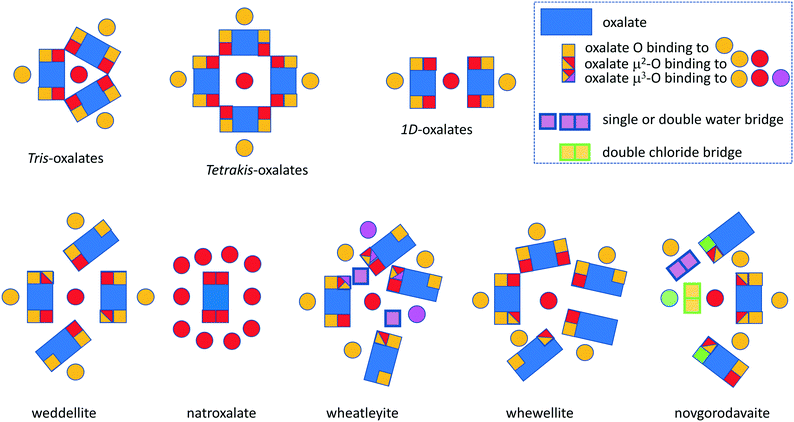Fig. 14 Schematic overview of the connectivity of the oxalates discussed in this article, including the tetrakis-oxalates only briefly mentioned.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

CLFD, FMAN, and LÖ thank the Swedish Research Council. We are grateful to Prof. Michael O'Keeffe for adding the new network topologies noa, mys, daz and hum to the RCSR database.

Notes and references

1. L. Öhrström and J. Covès, The Rhubarb Connection and Other Revelations: The Everyday World of Metal Ions, Royal Society of Chemistry, London, 2018.
2. I. Huskić, N. Novendra, D.-W. Lim, F. Topić, H. M. Titi, I. V. Pekov, S. V. Krivovichev, A. Navrotsky, H. Kitagawa and T. Friščić, Chem. Sci., 2019, 10, 4923–4929.
3. F. Y. Yi, H. J. Yang, X. Zhao, P. Y. Feng and X. H. Bu, Angew. Chem., Int. Ed., 2019, 58, 2889–2892.
4. B. Zhang, P. J. Baker, Y. Zhang, D. Wang, Z. Wang, S. Su, D. Zhu and F. L. Pratt, J. Am. Chem. Soc., 2018, 140, 122–125.
5. M. Darawsheh, L. A. Barrios, O. Roubeau, S. J. Teat and G. Aromí, Angew. Chem., Int. Ed., 2018, 57, 13509–13513.
6. P. K. Tsobnang, E. Hastürk, D. Fröhlich, E. Wenger, P. Durand, J. L. Ngolui, C. Lecomte and C. Janiak, Cryst. Growth Des., 2019, 19, 2869–2880.
7. C. F. N. Nguemdzi, F. Capet, J. Ngouné, G. Bebga, M. Foulon and J. Nenwa, J. Coord. Chem., 2018, 71, 1484–1496.
8. G. W. Burgers and W. Bragg, Proc. R. Soc. London, Ser. A, 1927, 116, 553–586.
9. A. F. Wells, Three-dimensional nets and polyhedra, John Wiley & Sons, New York, 1977.
10. A. F. Wells, Acta Cryst., 1954, 7, 535–544.
11. O. M. Yaghi, M. O'Keeffe, N. W. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Nature, 2003, 423, 705–714.
12. V. A. Blatov, L. Carlucci, G. Giani and D. M. Proserpio, CrystEngComm, 2004, 6, 377–395.
13. L. Öhrström and K. Larsson, Molecule-Based Materials The Structural Network Approach, Elsevier, Amsterdam, 2005.
14. L. Öhrström, Chem. – Eur. J., 2016, 22, 13758–13763.
15. L. Öhrström and K. Larsson, Dalton Trans., 2004, 347–353.
16. L. Öhrström and K. Larsson, Molecule-Based Materials: The Structural Network Approach, Elsevier, Amsterdam, 2005, ch. 12.
17. O. E. Piro and E. J. Baran, Crystallogr. Rev., 2018, 24, 149–175.
18. I. Huskic and T. Friscic, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2018, 74, 539–559.
19. B. Smith, 'Designer' materials found deep in Siberian permafrost, Cosmos, 2016, 08 AUGUST.
20. E. Stoye, Naturally occurring MOFs found in coal mine minerals, Chemistry World, RSC, 2016, 19 AUGUST.
21. I. Huskic, I. V. Pekov, S. V. Krivovichev and T. Friscic, Sci. Adv., 2016, 2, 7.
22. V. A. Blatov, A. P. Shevchenko and D. M. Proserpio, Cryst. Growth Des., 2014, 14, 3576–3586.
23. O. Delgado-Friedrichs and M. O'Keeffe, Acta Crystallogr., Sect. A: Found. Crystallogr., 2003, 59, 351–360.
24. M. O'Keeffe, M. A. Peskov, S. Ramsden and O. M. Yaghi, Acc. Chem. Res., 2008, 41, 1782–1789.
25. S. R. Batten, N. R. Champness, X. M. Chen, J. Garcia-Martinez, S. Kitagawa, L. Öhrström, M. O'Keeffe, M. P. Suh and J. Reedijk, Pure Appl. Chem., 2013, 85, 1715–1724.
26. A. Mizuno, Y. Shuku and K. Awaga, Bull. Chem. Soc. Jpn., 2019, 92, 1068–1093.
27. N. L. Rosi, J. Kim, M. Eddaoudi, B. Chen, M. O'Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 2005, 127, 1504–1518.
28. M. Clemente-León, E. Coronado and M. López-Jordà, Dalton Trans., 2013, 42, 5100–5110.
29. V. A. Blatov, M. O'Keeffe and D. M. Proserpio, CrystEngComm, 2010, 12, 44–48.
30. M. Clemente-León, E. Coronado, M. López-Jordà, G. Mínguez Espallargas, A. Soriano-Portillo and J. C. Waerenborgh, Chem. – Eur. J., 2010, 16, 2207–2219.
31. H.-Y. Shen, W.-M. Bu, D.-Z. Liao, Z.-H. Jiang, S.-P. Yan and G.-L. Wang, Inorg. Chem., 2000, 39, 2239–2242.
32. T. Endo, K. Kubo, M. Yoshitake, S.-i. Noro, N. Hoshino, T. Akutagawa and T. Nakamura, Cryst. Growth Des., 2015, 15, 1186–1193.
33. A. Ben Djamâa, M. Clemente-León, E. Coronado and M. López-Jordà, Polyhedron, 2013, 64, 142–150.
34. E. Coronado, J. R. Galán Mascarós, M. C. Giménez-López, M. Almeida and J. C. Waerenborgh, Polyhedron, 2007, 26, 1838–1844.
35. M. Clemente-León, E. Coronado and M. López-Jordà, Dalton Trans., 2010, 39, 4903–4910.
36. C. Borel, M. Ghazzali, V. Langer and L. Öhrström, Inorg. Chem. Commun., 2009, 12, 105–108.
37. J. T. Kloprogge, T. E. Bostrom and M. L. Weier, Am. Mineral., 2004, 89, 245–248.
38. V. Tazzoli and C. Domeneghetti, Am. Mineral., 1980, 65, 327–334.
39. A. R. Izatulina, V. V. Gurzhiy, M. G. Krzhizhanovskaya, M. A. Kuz'mina, M. Leoni and O. V. Frank-Kamenetskaya, Cryst. Growth Des., 2018, 18, 5465–5478.
40. L. R. Parent, C. H. Pham, J. P. Patterson, M. S. Denny, S. M. Cohen, N. C. Gianneschi and F. Paesani, J. Am. Chem. Soc., 2017, 139, 13973–13976.
41. M. Ghazzali, V. Langer, K. Larsson and L. Öhrström, CrystEngComm, 2011, 13, 5813–5817.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ce01187k

---