Desolvation process in the flexible metal–organic framework [Cu(Me-4py-trz-ia)], adsorption of dihydrogen and related structure responses

Abstract

Structural changes of the flexible metal–organic framework [Cu(Me-4py-trz-ia)] (1), which shows exceptionally high adsorption capacities for H₂ and CO₂, were characterized in detail by X-ray powder diffraction and single crystal structure analysis accompanied by DFT modelling after different solvent exchange procedures and at different stages of the activation process. Removal of solvent molecules from the pores within minutes results in a partially activated material that exhibits contracted pores due to hydrogen bonds between rearranged coordinating water molecules and the MOF framework. Further activation causes a release of all coordinating water molecules and, consequently, a re-opening of the pores to achieve the fully desolvated MOF with a similar unit cell as the non-activated, as-synthesized material. If all water molecules in the framework are replaced by methanol prior to activation, the pore contraction and re-expansion can be avoided, which allows not only a faster activation of the material at lower temperatures but also avoids fragmentation of the crystals of the empty framework. DFT calculations confirm the different activation routes, depending on solvent exchange procedures and kinetics of the water removal. Computed binding energies for H₂ adsorption in the fully activated framework are nearly independent of H₂ loading and adsorption position. Inelastic neutron scattering (INS) experiments at different H₂ loadings suggest simultaneous multiple adsorption sites occupancy at low loading levels which is in good agreement with the computational results. Most sensitive to the pore filling by hydrogen, at the microscopic level, appeared to be the rotational dynamics of the methyl group, as an intrinsic interactions probe.

---

Introduction

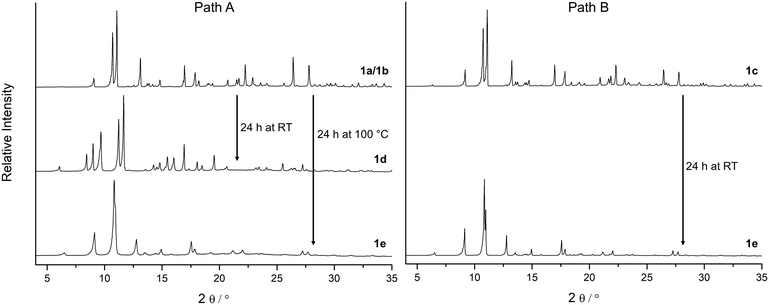
Based on the enormous variety of organic linkers in combination with various metal ions or secondary building units, metal–organic frameworks (MOFs) show a huge structural diversity leading to many potential applications.^1–3 With their high porosity and huge inner surface MOFs are considered for gas separation, gas storage, sensor applications, heterogeneous catalysis, proton conducting membranes, storage and controlled release of drugs or adsorptive heat storage. In order to make the pores accessible for guest molecules it is necessary to remove solvent molecules and other residues remaining from the synthesis. This is typically achieved by Soxhlet extraction using a low boiling solvent and subsequent activation in vacuum. According to S. Kitagawa, MOFs are categorized into three “generations”, depending on their behavior during removal of guest molecules.^4–6 Especially interesting are “third generation MOFs”: these compounds are structurally flexible and are regarded as soft porous crystals, they respond on external stimuli such as pressure,^7–12 temperature,^13–15 light^16–18 or adsorbed molecules^19,20 by structural changes. Structural flexibility in MOFs has become a subject of interest in recent years.^20–35

In 2011 we reported on synthesis, crystal structure and adsorption properties of a copper based MOF, [Cu(Me-4py-trz-ia)] (1), with pts topology.³⁶ This 3D coordination polymer is easily accessible as single crystals by synthesis under diffusion control and in multigram scale by reflux synthesis of copper(II)sulfate pentahydrate with 3-methyl-5-pyridine-4-yl substituted triazolyl isophthalic acid H₂(Me-4py-trz-ia) (Fig. 1) in water/acetonitrile. According to the single crystal structure analysis performed at room temperature the 3D pore system consists of narrow pore channels of about 250 × 600 and 550 × 550 pm. The calculated pore fraction of this MOF amounts to ca. 55% of the crystal volume, consistent with the results of adsorption measurements with various gases.³⁶E.g., the CO₂ adsorption isotherm is a typical type I isotherm according to the IUPAC classification; the CO₂ uptake determined gravimetrically amounts to 9.2 mmol g⁻¹ or 40.5 wt% CO₂ at 273 K and 0.1 MPa. Also the hydrogen uptake, 3.07 wt% H₂ at 77 K at ambient pressure is among the highest values reported to date under these conditions.^37,38 The asymmetric unit of 1 (space group P2₁/c) contains two crystallographically independent copper atoms on inversion centres. While Cu2 is [4 + 2]-coordinated by two triazol nitrogen and two carboxylate oxygen atoms in a square planar fashion with two additional weak interactions to the other oxygen atoms of the same carboxylate groups, Cu1 is in the centre of a square planar arrangement of two pyridine nitrogen and two carboxylate oxygen atoms. Surprising is the fact, that the isosteric heat of adsorption is almost independent of the degree of loading, although there are apparently open metal sites at the Cu^II centres. The independence of the adsorption enthalpy on the degree of loading suggests that the open metal sites are not the preferred positions for adsorption. This has been confirmed by simulations performed by Space et al.³⁹ According to their calculations, instead of sorption directly at the open metal sites, in this MOF H₂ and CO₂ adsorption should occur primarily between adjacent carboxylate oxygen atoms and between nearby methyl groups of the organic linkers in the 3D pore system. This behaviour is regarded as a consequence of the low partial positive charges of the copper atoms as determined by electronic structure calculations.³⁹ For these simulations the crystal structure of the solvent-free material is assumed to be equal to that of the as-synthesized MOF. However, the changes in the diffraction pattern upon activation indicate structural changes. Additionally, different treatments of the MOF prior to activation have a drastic effect on structural changes during activation in vacuum (Fig. 2 and SI-3‡). Herein we report on detailed combined single crystal and powder diffraction studies on samples of 1 after different solvent exchange procedures and after activation under various conditions. Furthermore, investigations of dihydrogen adsorption in 1 by DFT calculations and inelastic neutron scattering (INS) experiment are presented.

Fig. 1 Fragment of the crystal structure of 1 showing the coordination of the deprotonated ligand (Me-4py-trz-ia)²⁻ through nitrogen (blue) and oxygen (red) atoms to the copper sites Cu1 and Cu2.

Fig. 2 Depending on solvent molecules present in the framework of 1, X-ray diffraction patterns indicate structural changes during activation under vacuum. Path A: Water molecules at the Cu²⁺ centres in the as-synthesized material 1a and in 1b (incomplete solvent exchange with methanol) cause the formation of the phase 1d during the activation under vacuum before the fully activated state of 1e is reached. Path B: After a complete exchange of all solvent molecules by methanol (phase 1c) the transformation to phase 1d is not observed and the MOF can be activated at significantly lower temperatures to form 1e (air-dried samples of 1a, 1b and 1c show very similar PXRD patterns).

Results and discussion

Crystallographic studies

Since single crystal X-ray diffraction of as-synthesized crystals of 1a at 180 K resulted in poor data quality, the original dataset was measured in a solvent filled capillary at room temperature.³⁶ Interestingly, single crystal structure analysis at 213 K provides a diffraction pattern with sufficient data quality to solve and refine the crystal structure (Table 1). A phase transition at low temperature was confirmed by X-ray powder diffraction patterns of an air-dried sample of 1a collected at 293 K and 180 K (Fig. SI-1‡).

Table 1 Unit cell parameters and agreement factors obtained from single crystal structure analyses of samples directly after synthesis (1a), after solvent exchange (1b, 1c) and after a complete removal of all solvent molecules in the framework (1e). In case of partially activated phase 1d, the corresponding unit cell parameters and agreement factors were obtained from Rietveld analysis of the measured X-ray powder diffraction pattern

	1a	1b	1c	1d	1e
a The PLATON/SQUEEZE-routine^40 was applied.
Sample	Single crystal	Single crystal	Single crystal	Powder	Single crystal
Temperature	213 K	213 K	150 K	293 K	150 K
Space group	P21/c	P21/c	Pc	P21	P21/c
a/pm	1425.1(2)	1386.63(4)	1371.36(4)	1454.93(3)	1355.18(4)
b/pm	1339.9(2)	1323.50(4)	1322.70(5)	1193.95(1)	1391.61(4)
c/pm	1463.7(2)	1502.41(4)	1517.95(5)	1415.17(3)	1482.83(4)
β/°	93.00(1)	93.199(2)	93.415(3)	93.6939(5)	90.716(3)
V/10^6 pm^3	2790.9(7)	2752.9(1)	2748.5(2)	2453.20(7)	2796.2(1)
R int	0.0576	0.0456	0.0493	—	0.0502
R 1	0.032^a	0.056^a	0.044^a	—	0.059
wR2	0.074^a	0.197^a	0.117^a	—	0.177
R P	—	—	—	0.029	—
R wp	—	—	—	0.038	—

---

In contrast to the earlier structure analysis at RT, at 213 K water molecules (O5) could be localized as axial ligands extending the square planar coordination of Cu1 (Cu1–O1 196.5(2) pm; Cu1–N4 200.9(2) pm) to an elongated octahedron (Cu1⋯O5 261.1(3) pm). Weak O5–H5B⋯O2 hydrogen bonds (O⋯O 282.5(4) pm) are formed between these water molecules and the non-coordinating oxygen atoms of the monodentate carboxylate groups. Detailed pictures of the coordination spheres of the Cu^II centres are provided in Fig. 3 and in SI-7.‡ Since no further solvent molecules could be localized in the structure analysis, the PLATON/SQUEEZE-routine⁴⁰ was applied to take care of disordered solvent electron density. Unit cell parameters and agreement factors of the improved structure analysis of 1a are summarized in Table 1.

Fig. 3 Comparison of the coordination spheres of the Cu^II centres Cu1 and Cu2 in the framework of 1 after different treatments. I: Incomplete solvent exchange with methanol of the as-synthesized sample of 1a forming 1b (pores are filled with methanol, however water molecules at Cu1 are still present); II: complete solvent exchange with methanol forming 1c (water molecules at Cu1 are exchanged by one methanol molecule); III: activation under vacuum for 24 h at RT; IV: contact of 1c with humidity prior to activation under vacuum for 24 h at RT (a direct transformation from 1c (space group Pc) to 1d (space group P2₁) is considered unlikely); V: activation under vacuum for 24 h at 100 °C (an alternative representation of the coordination modes of Cu1 and Cu2, including thermal ellipsoids and bond lengths, is shown in Fig. SI-7‡).

According to the X-ray diffraction patterns in Fig. 2 solvent molecules have a strong influence on the behaviour of this MOF under vacuum and consequently on the time and temperature needed to activate this material. Furthermore, the crystallinity of the fully desolvated material 1e depends on the path that is passed during the activation. Transformation of the MOF along path A (Fig. 2; left part in Fig. 3) leads to fragmentation of the crystals resulting in a microcrystalline powder, while path B allows to yield 1e with preserved crystallinity. To investigate this important role of a proper solvent exchange for structural changes crystals of 1a were subjected to different solvent exchange procedures and characterised by X-ray single crystal structure analysis. Keeping the as-synthesized crystals 1a (synthesized in MeCN/H₂O) in methanol leads to an incomplete solvent exchange resulting in crystals 1b, while continuous solvent exchange and higher temperatures that prevail during a Soxhlet extraction give rise to material 1c. Unit cell parameters and agreement factors of 1b and 1c are given in Table 1. Single crystal structure analysis of 1b was performed at 213 K, because of a phase transition, similar to that described for phase 1a, which resulted in poor diffraction data quality at lower temperatures. Interestingly, phase 1c does not show such a temperature dependence. Solvent exchange in the pores of the MOF induces a similar shift of the unit cell parameters in 1b and 1c compared to those of the as-synthesized material 1a (shortening of axes a and b, extension of axis c), however, the crystal structures reveal some astonishing differences caused by the applied solvent exchange procedures (Fig. 3): Whereas the coordination modes of the Cu^II centres remain unchanged in 1b, with the water molecules O5 still coordinating to Cu1, in 1c these two water molecules are replaced by one methanol molecule coordinating in the axial position of a now square pyramidal arrangement around Cu1 (O9–Cu1 233.4(5) pm). Accordingly, due to the lack of inversion symmetry, the space group changes from P2₁/c to Pc in 1c. The distorted octahedral coordination environment of Cu2 is not effected by the solvent exchange. After applying the PLATON/SQUEEZE-routine⁴⁰ to account for the electron density in the pores, 316 electrons were found in the solvent accessible volume of 1b and 303 electrons in that of 1c, which corresponds to 18 and 17 uncoordinated methanol molecules per cell volume, respectively.

In order to investigate the effect of solvent molecules in this MOF on the behaviour of its structural response under vacuum, samples of 1a, 1b and 1c were carefully activated under various conditions. To prevent rehydration all activated samples were handled under N₂ atmosphere. While 1c only shows a slight colour change to another shade of blue during the activation under vacuum, samples of 1a and 1b undergo a noticeable transformation from a bluish violet to a light blue shade (phase 1d) within a few minutes (Fig. 4 and SI-5‡), accompanied by a strong fragmentation of the crystallites to a microcrystalline powder. Phase 1d remains at RT even after 24 h under vacuum (p = 10⁻³ mbar).

Fig. 4 Investigation of the phase transition of 1b to 1d by in situ powder XRD in vacuum at room temperature. PXRD patterns were collected every 6 s. Then for each pattern in this figure three successive patterns were merged to get a better signal-to-noise ratio. Please note: the phase transition occurs noticeably faster under normal activation conditions due to flow limitations within the in situ setup.

This fast phase transition was closely monitored by in situ PXRD experiments in a setup reported in ref. 20: a sample of 1b in a glass capillary (diameter 1.0 mm) was analysed by X-ray powder diffraction while connected to a high vacuum line. Fig. 4 depicts the changes in the diffraction patterns (4° < 2θ < 22°) within 30 minutes at high vacuum. According to these observations the phase transition from 1b to 1d proceeds within minutes at room temperature. Since reflections of phase 1b decrease in intensity while reflections of phase 1d increase, it can be concluded that the phase transition occurs in a particle by particle mode.

According to the unit cell parameters determined from powder diffraction data of phase 1d (Table 1) the unit cell shrinks by 11% upon applying vacuum, mainly due to contraction along the b axis. Based on this unit cell an appropriate structure model for phase 1d could be obtained by powder structure solution using the simulated annealing approach (EXPO2014 (ref. 41)) and was subsequently optimised by Rietveld refinement (R_p = 0.029, R_wp = 0.038; Table 1, Fig. SI-6; the corresponding crystallographic data is given in the ESI‡).

These results suggest that the phase transition from 1a and 1b to 1d is associated not only with a shrinking of the unit cell volume but also with a loss of inversion symmetry from space group P2₁/c to P2₁ and a significant change of the coordination modes of the Cu^II centres (Fig. 3). Mild activation induces a removal of one of the weakly coordinated water molecules at Cu1 in the axial position, which is now occupied by a carboxylate oxygen atom (Cu1⋯O6 273.9(8) pm). The remaining water molecule exhibits a significantly shorter bond to Cu1 (Cu1⋯O9(water) 222(2) pm) than in the as-synthesized structure and in 1b. Unexpectedly, the refined structure model of phase 1d reveals the coordination of one water molecule to Cu2 (Cu2⋯O10(water) 242(2) pm) during the activation process, while the weak interactions to the oxygen atoms of both coordinating carboxylate groups are released. It is worth mentioning that the Cu2⋯O4 distance of the copper atom to the carboxylate oxygen atom in one of the axial positions is 304.3(8) pm resulting rather in a square pyramidal [4 + 1] coordination environment at Cu2 than the [4 + 2] coordination of Cu1 and Cu2 in 1a/1b. It should be noted that the formation of 1d can also occur in the case of 1c, when the Soxhlet extracted MOF is exposed to humidity prior to activation, indicating a strong preference for the adsorption of water at the Cu centres instead of methanol. Therefore, a proper handling of the material after a complete solvent exchange is crucial.

Coordination of water molecules at both copper sites has a quite drastic effect on the pore dimensions in 1d (Fig. 5). The water molecules O9 and O10 are connected to adjacent non-coordinating oxygen atoms of carboxylate groups through distinct hydrogen bonds with O⋯O distances in the range of 260–290 pm causing a contraction of the cavities in b direction. This is in good agreement with the observed reduction of the b lattice parameter from 1339.9(2) pm in 1a and 1323.50(4) pm in 1b compared to 1193.95(1) pm in 1d.

Fig. 5 Shrinking of the cavities along the b axis in the partially activated phase 1d caused by hydrogen bonds (O⋯O ≈ 260–290 pm) between coordinating water molecules at both Cu²⁺ centres and adjacent carboxylate oxygen atoms (different than this projection might suggest there is no interaction between the coordinating water molecules in 1a/1b. The intermolecular distance of the water molecules is >750 pm).

As indicated by the diffraction patterns in Fig. SI-3,‡ further activation (for a longer period or at elevated temperatures) of this material under vacuum leads to the formation of at least one more unknown phase until the fully desolvated phase 1e is reached (after 24 h at 100 °C), probably a unit cell transformation connected with a stepwise removal of the coordinating water molecules at both Cu^II centres.

In contrast to 1a and 1b, activation of 1c for 24 h at room temperature already leads to the fully desolvated MOF 1e with significantly less fragmentation of the crystallites. Hence, it was possible to perform a single crystal structure analysis on a small crystal fragment of 1e. The unit cell parameters (Table 1) correspond to the parameters determined by indexing and Pawley refinement of the powder diffraction data of fully activated 1e (Tab. SI-2‡). The structure could be solved in space group P2₁/c and refined to an acceptable agreement factor R₁ = 0.059. The atomic positions are close to those of as-synthesized 1a; however, there are no solvent molecules binding to Cu²⁺ and there is no residual electron density originating from solvent molecules in the MOF pores. The simulated PXRD pattern based on the single crystal data of 1e is consistent with the measured diffraction patterns (Fig. SI-4‡). After complete activation of the material all coordinating water molecules are gone and both Cu²⁺ ions form weak Cu⋯O(carboxylate) bonds to the second oxygen atom of the coordinating carboxylate groups. In case of Cu2 the coordination environment corresponds to that of the non-activated phases. The inversion symmetry at the copper centres is restored. With regard to phase 1d, as a consequence of the removal of the water molecules involved in hydrogen bonds, the cavities expand again resulting in a unit cell similar to that of the non-activated compounds (similar unit cell parameters a, b and c, but smaller angle β). The non-activated phases can be fully restored by resolvation of the activated materials 1d and 1e indicating a reversible structural transformation.

This structural alterations during activation are accompanied by a noticeable change of the dihedral angles between the linker components (Fig. 6): whereas the benzene ring (blue) of the isophthalate group and the triazole ring (green) remain approximately perpendicular to each other (84.2–89.8°) during the activation process, the dihedral angles between the carboxylate groups and the benzene ring and between the triazole and pyridine groups (orange) change noticeably. These C–C bond rotations are depicted in a schematic way in Fig. 6. The pyridine groups (orange) experience a slight rotation; the dihedral angle (pyridine-triazole) change from 26.3° (average value in the non-activated phases 1a, 1b and 1c) to 14.9° and 3.4° in 1d and to 7.3° in the fully desolvated phase 1e, while the triazole groups (green) and the benzene rings (blue) show similar orientations in all frameworks.

Fig. 6 Schematic representation of the changes in the framework of 1 upon activation under vacuum, view along [010]. While the benzene rings (blue) of the isophthalic acid groups and the triazole rings (green) remain approximately in the same position, the pyridine rings (orange) exhibit a noticeable rotation during the activation of the MOF.

Temperature-dependent PXRD measurements (Fig. SI-8‡) of samples of 1b and 1c show similar behaviour upon thermal-only activation in glass capillaries. While the PXRD patterns of 1b indicate the formation of phase 1d at ca. 140 °C, which quickly transforms to a high-temperature phase at ca. 145 °C, the PXRD patterns of 1c show a continuous transition from 1c to 1e.

DFT simulation results

The strong interactions involving adsorbed water molecules and their influence on the MOF structural changes, for stoichiometric H₂O loadings in the vicinity of the Cu centres, were investigated by DFT simulations. For these simulations, the desolvated unit cell of 1a containing 140 atoms, distributed over 36 nonequivalent positions, was first fully relaxed by optimizing the lattice cell parameters and all atomic coordinates within space group P2₁/c, until the stresses acting on each atom decreased to below 1 meV Å⁻¹. The finally obtained lattice parameters were a = 1371.2, b = 1361.9, c = 1520.3 pm, β = 92.31° which are in quite good agreement with the experimental values of 1e (150 K) a = 1355.18(4), b = 1391.61(4), c = 1482.83(4) pm, β = 90.716(3)°. Additionally, the structure was also optimized with no symmetry restrictions as a check of the desolvated structure stability, within space group P1. The result was practically identical with the one relaxed in group P2₁/c. We then checked the binding of H₂O molecules near the two Cu^II sites and the corresponding effect on the shape of the framework unit cell. This is considered important, because the sites near the Cu^II centres bind water molecules much more strongly than the rest of the rather hydrophobic framework. Indeed, adsorption of two H₂O molecules at Cu1 (equivalent to the situation in 1a) results in a computed binding energy of 60 kJ mol⁻¹. The calculated Cu–O distance for water molecules coordinated at this site, 263.5 pm, is in good agreement with single crystal structure data of 1a (Cu1–O5 261.3(3) pm). Including two water molecules near both Cu sites (Cu1⋯O_W 317.1 pm; Cu2⋯O_W 329.2 pm), due to attractive H₂O⋯H₂O interactions and the additional network of hydrogen bonds between water molecules as well as between water molecules and oxygen atoms of the carboxylate ligands, amounts to 66 kJ mol⁻¹. This model leads to a significant unit cell deformation with final relaxed lattice parameters a = 1243 pm, b = 1334 pm, c = 1646 pm, and β = 93.39°, which would very likely cause crystal cracking. In case of H₂O coordination only to Cu1, the a and c lattice parameters are slightly elongated from 1371 to 1390 pm and from 1520 to 1541 pm, respectively, while the b axis shrinks from 1334 to 1307 pm and angle β increases slightly from 92.31 to 94.00°. These relatively small unit cell deformations caused by H₂O coordination are roughly in agreement with single crystal structure data of the non-activated phases and the fully desolvated 1e. In a different test, a structure model of phase 1d, obtained from diffraction experiments, was used as a starting model for DFT simulations. Included is one H₂O molecule for each Cu centre with reduced symmetry in space group P2₁. This appears the most stable hydrated structure with a binding energy of 90 kJ mol⁻¹, the two H₂O molecules being hydrogen bonded to the nearby carboxylate oxygen atoms and between each other residing in the neighbourhood of Cu1 and Cu2. The relaxed lattice parameters, a = 1484.2 pm, b = 1197.0 pm, c = 1396.1 pm, β = 94.26°, are in good agreement to the parameters derived from the powder pattern of phase 1d (Table 1). This structure was also further relaxed in space P1 group without any significant structural changes. Driving the crystallites of the material to the state with just chemisorbed water molecules left near the Cu sites by evacuation of the physisorbed solvent in the pore interiors (phase 1d, space group P2₁), and then the release of these H₂O molecules to form phase 1e (P2₁/c) might be two crucial steps, causing jumpwise lattice deformation and crystal rupture.

The affinity of different framework parts and adsorption sites towards molecular H₂ was estimated by simulating the addition of different amounts of hydrogen molecules into the unit cell, while keeping the original symmetry (space group P2₁/c) up to a maximum loading of 28 molecules H₂ per unit cell corresponding to seven crystallographically distinct adsorption sites. For the maximum loading we added also an H₂ molecule in the unit cell centre, reduced the P2₁/c symmetry to space group P1, and relaxed the resulting structure. For comparison, a similar test was also done for the 28 H₂ molecules per unit cell loading which did not result in any significant geometry change. The individual stabilities of H₂ at sites labeled I to IV (Fig. 7) were also calculated by relaxing all atomic coordinates of the MOF structure containing only 4 H₂ molecules positioned at either I, II, III, or adsorption site IV.

Fig. 7 Representation of the seven distinct adsorption sites from DFT simulation for the adsorption of dihydrogen in the pores of 1e. Site I exhibits the nearest distance to one of the Cu^II centres (Cu1) with ca. 270 pm and is close to a carboxylate oxygen atom with ca. 240 pm. Sites II, III and VI are close to a carboxylate group as well with distances of about 250 pm.

The binding energy E_b of only 2 kJ mol⁻¹ H₂ for site V (near the phenyl ring and the pyridine ring of the ligand, Fig. 7) appears very weak on its own. Sites VI and VII were tested only together with all the earlier sites populated. A positive sign for E_b is adopted for attractive interactions. This was calculated as

E_b(H₂) = E_tot(MOF + nH₂) − E_tot(MOF) − nE_tot(H₂) (1)

The total energy for one of the n molecules of the guest species, E_tot(H₂), with geometry relaxed in the same theoretical setup, was evaluated in a box of 16 × 16 × 16 ų size. For the fully optimized unit cell of the activated form of 1e loaded with 29 H₂ molecules the structure was re-optimized in space group P1. Site specific binding energies for the first four adsorption sites that reside nearby different parts of the porous framework are displayed in Fig. 8(top). In Fig. 8(bottom) the site averaged binding energy is shown as a function of the total hydrogen loading. Notably, the computational results suggest that the adsorption positions near the internal surface of the framework, i.e. close to different parts of the ligands and the inorganic units represent a set of sites of very similar strength. This is in agreement with the flat Q_stvs. hydrogen content dependence experimentally observed³⁶ and found by the calculations by Space et al.³⁹ assuming a rigid framework. In reality, i.e. at finite temperatures, stoichiometric site occupancy is unlikely and the adsorbed H₂ molecules, even at temperatures as low as 77 K, due to entropy contributions, should be distributed over most of the crystallographically different positions, thus minimizing the free energy of the system. Thus, a non-stoichiometric site occupancy, even at relatively low temperatures, is expected.

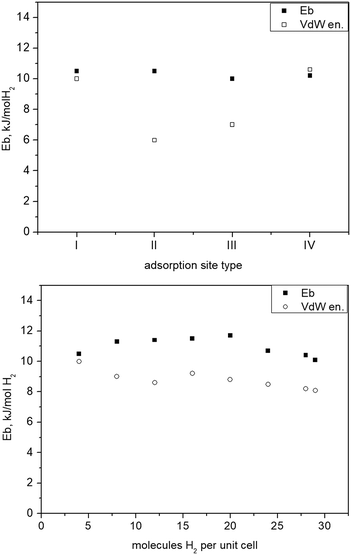Fig. 8 Top: Binding of H₂ at different structural sites of 1 (see Fig. 7) representing different possible individual adsorption sites stable on its own; bottom: binding energy vs. H₂ total loading given as number of molecules per unit cell.

It is quite remarkable, that from the lowest up to the maximum test loading, corresponding to about 3.6 wt% H₂, the binding energy remains nearly constant at about 10 kJ mol⁻¹ H₂, a particular signature of this material previously unseen for any other MOF. The computed binding energy is in very good agreement to the measured dihydrogen Q_st,³⁶ remaining nearly constant with the H₂ loading. This fact also suggests that the adsorption of hydrogen is not accompanied by any energy losses associated with framework deformations. It is in agreement with the crystallographic studies that show that the structure of fully activated MOF 1e in its open form is very close to that of the solvated open form 1a, whereas the unit cell of the partly desolvated phase 1d is significantly different. Filling the cell with H₂ molecules causes only minimal lattice changes (Fig. SI-9‡), the binding energy E_bvs. loading curve remains flat above 10–12 molecules per unit cell.

Inelastic neutron scattering studies

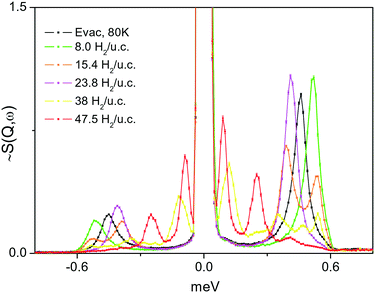
A series of INS spectra of H₂ adsorbed in the framework of 1e, corresponding to different H₂ loadings, is shown in Fig. 9(top). Even at the lowest loading, where one might expect a single site or just Cu^II sites occupancy, presumably being the strongest binding sites, a scenario observed⁴² for H₂ adsorbed in HKUST-1 containing paddle wheel type Cu^II sites, here some very broad and complex spectra are seen instead. Fig. 9(bottom) compares the present INS signal obtained from the material dosed with 4 H₂ per unit cell to that of H₂ adsorbed in CPO-27-Cu, where simultaneous adsorption on at least two framework sites was anticipated from sorption thermodynamics measurements, INS and DFT simulations.⁴³ Except the very low energy portion of the spectra, below 6–7 meV, the two spectra are qualitatively very similar with some small, about 1 meV, upward shift of the INS transitions for H₂ in 1. Clearly, the adsorbed hydrogen is distributed over more than one type of adsorption positions. Note that, as suggested by our DFT calculations, the site labelled II (near Cu2, in the vicinity of the CH₃ groups), is better represented as a carboxylate oxygen atom binding the H₂ molecule in an end on fashion. Such a simultaneous multisite adsorption was also found in CPO-27-Cu⁴³ by both DFT simulations and neutron diffraction of H₂ adsorbed at the primary Cu^II and the secondary adsorption sites, represented by oxygen atoms. The Cu–H₂ distance, according to DFT simulations on the CPO-27-Cu materials,⁴³ was about 280 pm. In the present simulations this distance is very similar, 277 and 296 pm from the Cu^II centre to the two protons of the molecule, which appears somewhat off-site positioned, due to the presence of the oxygen atom of the nearby carboxylate ligand. Therefore, the similarities in the corresponding two INS spectra in the range above 8 meV, in Fig. 9(bottom), may be attributed to the fact that they originate from H₂ molecules adsorbed at similar adsorption sites formed by Cu^II centers and oxygen atoms. Notably, the simulation studies predict a large enough distance between the Cu centre and this carboxylate ligand leaving its oxygen atom at 276.5 pm, thus making the Cu^II site accessible for small molecules like H₂. While the INS intensity above 8 meV shows the same complex behavior for all loadings, suggesting multiple site occupancy of the MOF voids, the features at <8 meV show an upward shift with increasing loading (Fig. 9, top). This behaviour may be attributed to torsional transitions of the CH₃ groups in the solid, whose rotational motion may become increasingly hindered by either adsorbed nearby H₂ molecules and/or significant change in the shape of the unit cell. Consequently, the rotational hindering potential felt by the CH₃ moieties increases upon progress of the adsorption process. The corresponding INS broad bands in the range 2–6 meV clearly appear first at a loading of 8 H₂ per unit cell, corresponding to 2 H₂ molecules per Cu^II centre (the CH₃ groups are vicinal only to Cu2). To check this hypothesis, the low energy spectra in the range below 1 meV, where the CH₃ rotational tunnelling lines are expected, are studied. The 0 → 1 free rotational transition of CH₃ is expected at ±0.65 meV.⁴⁴ The INS spectra within ±1 meV were measured using incident neutrons with a wavelength of 7 Å, for several loadings starting from 8 H₂ u.c.⁻¹ and then as indicated in the legend of Fig. 10. At the second lowest loading, measured in this regime, 2 H₂/Cu (8 H₂ u.c.⁻¹), the CH₃ transition is observed at about 0.52 meV, tailing towards lower energies. This shape may suggest some CH₃ group environment heterogeneity and generally very weak hindering barriers as seen in the data in Table 2.

Fig. 9 Top: INS spectra of different amounts of H₂ adsorbed at 1e; bottom: comparison between spectra of 1e with low H₂ concentration with the rigid hexagonal MOF CPO-27-Cu, whose SBU is based on pentacoordinated Cu^II centres.

Fig. 10 INS spectra in the low energy range showing CH₃ group tunnelling transitions in the MOF structure of 1e, loaded with different amounts of H₂. The black curve is the spectrum recorded after the material was evacuated for about 1 h at 80 K.

Table 2 CH₃ rotational tunnelling and librational transitions data for different H₂ loadings. ω_T is the energy of the observed tunnelling peak, Fig. 10, V₃ is the computed from that threefold rotational barrier, A0 → E1, and A0 → A1 are the librational transitions between the ground and the first excited states of the hindered CH₃ rotor, and Ω_L is the approximate energy of the INS observed intensity attributed to the computed librational transitions

H2 loading, H2 per unit cell	ω T, meV INS, Fig. 10	V 3, meV	A0–E1, meV	A0–A1, meV	Ω L, meV INS, Fig. 9
8.0	0.52	3.3	2.6	6.1	2.4 ÷ 7
15.4	0.39, 0.53	5.2, 3.0	3.3, 2.5	6.3, 6.1	2.4 ÷ 7
23.8	0.41	4.9	3.1	6.3	4 ÷ 7
47.5	0.25, 0.09	7.9, 14.1	4.4, 6.8	6.8, 8.2	4 ÷ 8.5
Evac. 80 K	0.046	4.1	2.9	6.2	3.0, 6.2

---

From the lowest energy part of the measured INS spectra, Fig. 10, and by solving the one-dimensional Schrödinger equation with a perturbation potential V of the form

which reduces to the well-known Mathieu equation, it is possible to derive the corresponding CH₃ group rotational frequencies. By comparison to the observed INS tunnelling peak positions, the corresponding rotational barriers, i.e. V₃, as well as the librational frequencies can be derived. Thus the measurement of the CH₃ rotational tunnelling transitions, apart from a direct measurement of the H₂ loading and related interactions, aids the assignment of the higher energy INS spectra, e.g., in the range 2–6 meV. Within this 1D rotational hindering model, the INS peak at about 0.52 meV corresponds to a relatively low hindering barrier V₃, with a magnitude of only 3.3 meV. The corresponding librations (torsional transitions) should then be expected at 2.6 meV (m = 1 → 2) and 6.1 meV (m = 0 → 3) in very good agreement with the observed bands (Fig. 9). CH₃ tunnelling and librational data are summarized in Table 2. Notably, and as could be expected for these relatively low rotational barriers,⁴⁴ the doublet nature of the librational states is resolved and therefore two inelastic bands are observed in each spectrum in Fig. 9 seen at about 2–3 and 5–6 meV. At the highest H₂ loadings the crowding of H₂ molecules increases the hindering effect on the CH₃ groups, leading to an increased rotational barrier (Fig. 10 and Table 2). As a result, the librational transitions move to higher energy and nearly merge (Fig. 9). On the other hand, even at the highest loadings two sharp CH₃ rotational tunnelling lines are observed in the INS spectrum in Fig. 10. These two lines must correspond to two CH₃ moieties that experience different well-defined rotational barriers due to different local environments. An attempt to scan the rotational potential using the above described DFT based methodology, however, failed dramatically, even in the case of the fully desolvated material, suggesting much higher, an order of magnitude, hindrance than the experimentally observed. This most probably is due to a coupling of the librational motion of the CH₃ groups to framework phonons which results in a large hindrance relaxation. This might also be the cause for the relatively large width of the librational lines. In the presence of many weakly bound H₂ molecules the coupling mechanism would become even more complicated, especially when taking into account that the perfect order, anticipated in the model studies, may and probably is not occurring in reality where a significant level of adsorbate spatial disorder could be present – a problem that is very difficult to tackle even with the present microscopic techniques.

Conclusions

Insight into the complex structural behaviour of the MOF [Cu(Me-4py-trz-ia)] during the desolvation of the framework shows the important role of a proper solvent exchange prior to activation. An incomplete solvent exchange by methanol results in a shrinking of the pores during activation induced by hydrogen bonding between remaining coordinating water molecules at the Cu^II centres and adjacent carboxylate oxygen atoms at the opposite site of the pores. As a consequence, not only longer activation times or higher temperatures are needed to fully desolvate the MOF but also fragmentation of the crystals occurs. Single crystal structure analysis of the empty framework obtained by complete solvent exchange and subsequent evacuation reveals a structure similar to that of the as-synthesized material, where the former positions of the coordinating water molecules are occupied by weak interactions with carboxylate oxygen atoms. Despite changes in space group symmetry, in all these crystal structures the network connectivity and topology (pts) remain unchanged.

DFT simulations on the H₂ adsorption site diversity and related thermodynamics in the fully relaxed activated MOF structure, at different loadings, show a binding energy almost independent of H₂ loading, in excellent agreement to the experimental observation. This is an indirect evidence for the relatively rigid framework behaviour not involving energy losses due to structure deformations in case of H₂ adsorption. According to inelastic neutron scattering (INS) studies of the adsorbed hydrogen dynamics below 4 K, [Cu(Me-4py-trz-ia)] in its fully activated form (1e) retains its full porosity. However, the adsorbed H₂ interacts only weakly with the MOF with no strong preference to a particular adsorption site. Very similar complex INS spectra of H₂ at different loadings from zero up to the complete pore filling were obtained, suggesting a multisite simultaneous adsorption, with no significant host framework structural changes. The pore filling was additionally monitored through the observation of the CH₃ groups rotational tunnelling, which experience an increasingly larger hindering to rotation with progressive hydrogen loading.

Our results bring new insights into the solvent influence and the behaviour during activation of [Cu(Me-4py-trz-ia)] as a structurally flexible MOF and might contribute to a better understanding of the structural behaviour of other flexible MOFs in dependence on solvent or guest molecules and preparative procedures.

Experimental section

Synthesis of 1a was performed according to ref. 36. By adding one drop of hydrochloric acid, larger crystals, suitable for X-ray single crystal diffraction experiments, could be obtained under solvothermal conditions in high quantities. Details are given in the ESI.‡ Crystals of 1b were obtained after solvent exchange of crystals of 1a with methanol 5 times over a period of 5 days at RT, whereas crystals of 1c were received by continuous Soxhlet extraction with anhydrous methanol for 5 days. Crystals of 1e for structure analysis were obtained by activation of crystals of 1c in vacuum at room temperature for 24 h.

Crystallographic data

Single crystal structure analyses were performed on a STOE IPDS-1 image plate diffractometer system using a sealed Mo X-ray tube (Mo-K_α, λ = 71.073 pm) (crystal of 1a) and on a STOE STADIVARI using an X-ray microsource (Cu-K_α, λ = 154.186 pm) (crystals of 1b, 1c and 1e). The data sets were processed with the program STOE X-AREA.⁴⁵ The structures were solved by direct methods and refined using SHELX.⁴⁶ The coordinates of all non-hydrogen atoms of the framework were refined with anisotropic thermal parameters. Hydrogen atoms of the framework were included in idealized positions. The SQUEEZE routine of the program PLATON was applied in case of 1a, 1b and 1c.⁴⁰ The program DIAMOND 3.2k was used to visualize the structures.⁴⁷ The data are summarized in the ESI.‡ CCDC 1922322–1922325 contains the supplementary crystallographic data for single crystals of 1a, 1b, 1c and 1e in this paper. The data for 1d (powder diffraction) are deposited under CCDC 1949910. The PXRD measurements were carried out on a STOE Stadi-P diffractometer equipped with a sealed Cu X-ray tube and a germanium (111) monochromator crystal (Cu-K_α1 radiation, λ = 154.060 pm). The crystal structure of 1d was determined from powder diffraction data. Space group determination and structure solution were done with EXPO2014.⁴¹ A reasonable structure model could be obtained by the simulated annealing approach in space group P2₁ using the derived lattice parameters from the indexing procedure. For the starting structure model two linker molecules and two copper ions were given as fragments. Since the activation is obviously not completed at this stage two water molecules were added as fragments to the starting model. Torsion angles of the linker molecules were not restrained during this process. The obtained structure model was refined by the Rietveld method using TOPAS.⁴⁸ In the course of refinement the linker molecules were treated as rigid bodies using the Z-matrix notation allowing the translation and the rotation of the molecules and all torsion angles to be refined freely. Atomic positions of the Cu²⁺ ions and the water molecules were not constrained/restrained during the refinement.

DFT based simulations

DFT simulations were performed using the Perdew–Burke–Ernzerhof (PBE) parametrization⁴⁹ of the generalized gradient approximation (GGA) with the Abinit (version 8) software package.^50,51 The electron density was represented with the aid of the projector augmented wave (PAW) formalism⁵² with a kinetic energy cut-off on the plane wave part of 820 meV (30 Ha) and on a 2 × 2 × 2 Monkhorst–Pack shifted k-point grid. Only spin unpolarised calculations were done, considered to be accurate enough for structure and binding energetics. Self-interaction and correlation effects on Cu^II 3d electrons were corrected by applying Hubbard U (7.5 eV) and correlation J (0.98 eV) parameters as suggested in the original procedure development^53,54 implemented in Abinit. As previously demonstrated,⁵³ dispersive interactions are significant and often even dominating in these types of guest–host systems, and were taken into account here by means of the Grimme D2 correction.⁵⁵

Inelastic neutron scattering (INS)

INS has proven as a powerful method to study adsorption sites, their specific shapes and bond strengths through the individual rotational dynamics of both physisorbed and chemisorbed H₂.^56–58 This comes from the fact that the neutron scattering cross section of hydrogen is much larger than that of most other substances and this determines to a large extent the intensity of the first rotational transition from J = 0 to J = 1 of molecular hydrogen, which is expected at about 120 cm⁻¹ if no hindrance to the rotational motion of the molecule is exerted, e.g., by the nearby surface potential or neighbouring molecules. Thus at low temperatures (below 20 K) due to quantum mechanical symmetry restrictions and in thermodynamic equilibrium, more than 99% of the adsorbate is expected in its ground rotational state, i.e. the singlet J = 0 state. Then the only observable transition, or the one of significant probability, is to the first excited, in case of free rotation, the triply degenerate state J = 1. Depending on the shape and strength of each adsorption site potential the J = 1 state is no longer degenerate, and the way this happens, i.e. the magnitudes of the splitting and shift of the m = 0, m = +1 and m = −1 substrates of the J = 1 manifold, is indicative for the variety of the available adsorption sites and their strengths. Thus physisorption H₂ adducts, with typical stabilities in the range 5–13 kJ mol⁻¹, usually show INS lines in the energy region above a few meV.^59–61 Strong adsorption, of order of a few tens of kJ mol⁻¹, with significant orbital interactions between the adsorbed H₂ molecule and the adsorption site constituents, i.e. chemisorption, results in INS lines well below 1 meV (ref. 62) with the gas phase reversibly forming Cu^I–H₂ complexes in the ZSM-5 zeolite showing the rotational H₂ line at 0.1 meV (ref. 58) and a corresponding heat of adsorption around 40 kJ mol⁻¹.⁶³ To test the site diversity and strengths in [Cu(Me-4py-trz-ia)] we performed H₂in situ high resolution INS experiments at the TOFTOF instrument⁶⁴ at the Heinz Maier-Leibnitz-Zentrum, Garching, Germany. A sample of 1.3 g dry weight material of 1 (Soxhlet extracted with methanol) was activated prior to the experiments under dynamic vacuum, provided by a turbo molecular pump, at 35 °C for about 20 h directly in an aluminium scattering cell connected to a gas capillary line, mounted at a special centre stick, suited for the instrument closed cycle refrigerator (CCR), to control the sample temperature during the scattering experiments. After cooling to 100 K the first H₂ dosing was initiated and the adsorption process was equilibrated over the course of the continuous cooling down to 3.5 K. The corresponding spectrum of the sample dosed with 3 mmol H₂, corresponding to a fractional occupancy 0.9 of the Cu centers, which equals to 3.6 H₂ (0.46 wt%) molecules per unit cell, was measured at 3.5 K using neutrons with an incident wavelength of 1.8 Å. Further dosings of 6.7, 13, 20, 32, and 40 mmol H₂ (1.03, 1.98, 3.01, and 5.84 wt%) were introduced and equilibrated at temperatures between 70 and 23 K. The corresponding spectra were measured at the base temperature of 3.5 K, again using a monochromatic incident neutron beam with wavelengths of 1.8 and 7 Å.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge financial support by Deutsche Forschungsgemeinschaft and the University of Leipzig (PbF-1). The authors thank Jens Moellmer and Marcus Lange (Institut für Nichtklassische Chemie e.V., Leipzig, Germany) for the cooperation in the construction of the setup for in situ powder XRD experiments. With respect to the neutron scattering experiments, this work is based upon experiments performed at the TOF/TOF instrument operated by the FRM II at the Heinz Maier-Leibnitz Zentrum (MLZ), Garching, Germany. The computational work was supported by the Bulgarian Ministry of Education and Science under the National Scientific Program “Information and Communication Technologies for a Single Digital Market in Science, Education and Security (ICTinSES)” (grant agreement DO1-205/23.11.18). P. A. G. also wishes to acknowledge access to supercomputing facilities (NESTUM cluster funded by the ERDF Project BG161PO003-1.2.05-0001-C0001) at Sofia Tech Park, Sofia, Bulgaria, provided by the Faculty of Physics at the University of Sofia, Bulgaria.

References

1. H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444.
2. C. Pettinari, F. Marchetti, N. Mosca, G. Tosi and A. Drozdov, Polym. Int., 2017, 66, 731–744.
3. The Chemistry of Metal-Organic Frameworks, ed. S. Kaskel, Wiley-VCH, Weinheim, 2016.
4. S. Kitagawa, R. Kitaura and S.-i. Noro, Angew. Chem., Int. Ed., 2004, 43, 2334–2375.
5. S. Horike, S. Shimomura and S. Kitagawa, Nat. Chem., 2009, 1, 695–704.
6. S. Kitagawa and M. Kondo, Bull. Chem. Soc. Jpn., 1998, 71, 1739–1753.
7. V. Bon, I. Senkovska, D. Wallacher, D. M. Többens, I. Zizak, R. Feyerherm, U. Mueller and S. Kaskel, Inorg. Chem., 2014, 53, 1513–1520.
8. V. Bon, I. Senkovska, D. Wallacher, A. Heerwig, N. Klein, I. Zizak, R. Feyerherm, E. Dudzik and S. Kaskel, Microporous Mesoporous Mater., 2014, 188, 190–195.
9. S. Yang, X. Lin, W. Lewis, M. Suyetin, E. Bichoutskaia, J. E. Parker, C. C. Tang, D. R. Allan, P. J. Rizkallah, P. Hubberstey, N. R. Champness, K. M. Thomas, A. J. Blake and M. Schröder, Nat. Mater., 2012, 11, 710–716.
10. N. Rosenbach Jr, A. Ghoufi, I. Déroche, P. L. Llewellyn, T. Devic, S. Bourrelly, C. Serre, G. Férey and G. Maurin, Phys. Chem. Chem. Phys., 2010, 12, 6428–6437.
11. C. Serre, S. Bourrelly, A. Vimont, N. A. Ramsahye, G. Maurin, P. L. Llewellyn, M. Daturi, Y. Filinchuk, O. Leynaud, P. Barnes and G. Férey, Adv. Mater., 2007, 19, 2246–2251.
12. M. Handke, H. Weber, M. Lange, J. Möllmer, J. Lincke, R. Gläser, R. Staudt and H. Krautscheid, Inorg. Chem., 2014, 53, 7599–7607.
13. S. Henke, A. Schneemann and R. A. Fischer, Adv. Funct. Mater., 2013, 23, 5990–5996.
14. L. D. DeVries, P. M. Barron, E. P. Hurley, C. Hu and W. Choe, J. Am. Chem. Soc., 2011, 133, 14848–14851.
15. I. Grobler, V. J. Smith, P. M. Bhatt, S. A. Herbert and L. J. Barbour, J. Am. Chem. Soc., 2013, 135, 6411–6414.
16. J. W. Brown, B. L. Henderson, M. D. Kiesz, A. C. Whalley, W. Morris, S. Grunder, H. Deng, H. Furukawa, J. I. Zink, J. F. Stoddart and O. M. Yaghi, Chem. Sci., 2013, 4, 2858.
17. A. Modrow, D. Zargarani, R. Herges and N. Stock, Dalton Trans., 2011, 40, 4217–4222.
18. N. Yanai, T. Uemura, M. Inoue, R. Matsuda, T. Fukushima, M. Tsujimoto, S. Isoda and S. Kitagawa, J. Am. Chem. Soc., 2012, 134, 4501–4504.
19. T. Loiseau, C. Serre, C. Huguenard, G. Fink, F. Taulelle, M. Henry, T. Bataille and G. Férey, Chemistry, 2004, 10, 1373–1382.
20. M. Lange, M. Kobalz, J. Bergmann, D. Lässig, J. Lincke, J. Möllmer, A. Möller, J. Hofmann, H. Krautscheid, R. Staudt and R. Gläser, J. Mater. Chem. A, 2014, 2, 8075–8085.
21. A. Schneemann, V. Bon, I. Schwedler, I. Senkovska, S. Kaskel and R. A. Fischer, Chem. Soc. Rev., 2014, 43, 6062–6096.
22. J.-P. Zhang, P.-Q. Liao, H.-L. Zhou, R.-B. Lin and X.-M. Chen, Chem. Soc. Rev., 2014, 43, 5789–5814.
23. H. J. Choi, M. Dincă and J. R. Long, J. Am. Chem. Soc., 2008, 130, 7848–7850.
24. S. Galli, N. Masciocchi, V. Colombo, A. Maspero, G. Palmisano, F. J. López-Garzón, M. Domingo-García, I. Fernández-Morales, E. Barea and J. A. R. Navarro, Chem. Mater., 2010, 22, 1664–1672.
25. S. S. Mondal, A. Bhunia, I. A. Baburin, C. Jäger, A. Kelling, U. Schilde, G. Seifert, C. Janiak and H.-J. Holdt, Chem. Commun., 2013, 49, 7599–7601.
26. S. S. Mondal, A. Bhunia, A. Kelling, U. Schilde, C. Janiak and H.-J. Holdt, Chem. Commun., 2014, 50, 5441–5443.
27. E. Quartapelle Procopio, T. Fukushima, E. Barea, J. A. R. Navarro, S. Horike and S. Kitagawa, Chem. – Eur. J., 2012, 18, 13117–13125.
28. C. Reichenbach, G. Kalies, J. Lincke, D. Lässig, H. Krautscheid, J. Moellmer and M. Thommes, Microporous Mesoporous Mater., 2011, 142, 592–600.
29. S. Henke, A. Schneemann, A. Wütscher and R. A. Fischer, J. Am. Chem. Soc., 2012, 134, 9464–9474.
30. S. Henke, R. Schmid, J.-D. Grunwaldt and R. A. Fischer, Chem. – Eur. J., 2010, 16, 14296–14306.
31. W. Yang, A. J. Davies, X. Lin, M. Suyetin, R. Matsuda, A. J. Blake, C. Wilson, W. Lewis, J. E. Parker, C. C. Tang, M. W. George, P. Hubberstey, S. Kitagawa, H. Sakamoto, E. Bichoutskaia, N. R. Champness, S. Yang and M. Schröder, Chem. Sci., 2012, 3, 2993–2999.
32. R. Medishetty, D. Jung, X. Song, D. Kim, S. S. Lee, M. S. Lah and J. J. Vittal, Inorg. Chem., 2013, 52, 2951–2957.
33. C. Serre, F. Millange, C. Thouvenot, M. Noguès, G. Marsolier, D. Louër and G. Férey, J. Am. Chem. Soc., 2002, 124, 13519–13526.
34. J. Lincke, D. Lässig, J. Moellmer, C. Reichenbach, A. Puls, A. Moeller, R. Gläser, G. Kalies, R. Staudt and H. Krautscheid, Microporous Mesoporous Mater., 2011, 142, 62–69.
35. S. S. Mondal, S. Dey, I. A. Baburin, A. Kelling, U. Schilde, G. Seifert, C. Janiak and H.-J. Holdt, CrystEngComm, 2013, 15, 9394.
36. D. Lässig, J. Lincke, J. Moellmer, C. Reichenbach, A. Moeller, R. Gläser, G. Kalies, K. A. Cychosz, M. Thommes, R. Staudt and H. Krautscheid, Angew. Chem., Int. Ed., 2011, 50, 10344–10348.
37. H. W. Langmi, J. Ren, B. North, M. Mathe and D. Bessarabov, Electrochim. Acta, 2014, 128, 368–392.
38. H. Li, K. Wang, Y. Sun, C. T. Lollar, J. Li and H.-C. Zhou, Mater. Today, 2018, 21, 108–121.
39. K. A. Forrest, T. Pham, K. McLaughlin, A. Hogan and B. Space, Chem. Commun., 2014, 50, 7283–7286.
40. A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7–13.
41. A. Altomare, C. Cuocci, C. Giacovazzo, A. Moliterni, R. Rizzi, N. Corriero and A. Falcicchio, J. Appl. Crystallogr., 2013, 46, 1231–1235.
42. Y. Liu, H. Kabbour, C. M. Brown, D. A. Neumann and C. C. Ahn, Langmuir, 2008, 24, 4772–4777.
43. M. H. Rosnes, M. Opitz, M. Frontzek, W. Lohstroh, J. P. Embs, P. A. Georgiev and P. D. C. Dietzel, J. Mater. Chem. A, 2015, 3, 4827–4839.
44. M. Prager and A. Heidemann, Chem. Rev., 1997, 97, 2933–2966.
45. Stoe & Cie GmbH, X-Area, Darmstadt, 2016.
46. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122.
47. K. Brandenburg, Diamond 3.2k, Crystal Impact GbR, Bonn, 2014.
48. A. Coelho, TOPAS, Bruker AXS GmbH, Karlsruhe, 2014.
49. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985.
50. X. Gonze, B. Amadon, P.-M. Anglade, J.-M. Beuken, F. Bottin, P. Boulanger, F. Bruneval, D. Caliste, R. Caracas, M. Côté, T. Deutsch, L. Genovese, P. Ghosez, M. Giantomassi, S. Goedecker, D. R. Hamann, P. Hermet, F. Jollet, G. Jomard, S. Leroux, M. Mancini, S. Mazevet, M. J. T. Oliveira, G. Onida, Y. Pouillon, T. Rangel, G.-M. Rignanese, D. Sangalli, R. Shaltaf, M. Torrent, M. J. Verstraete, G. Zerah and J. W. Zwanziger, Comput. Phys. Commun., 2009, 180, 2582–2615.
51. F. Bottin, S. Leroux, A. Knyazev and G. Zérah, Comput. Mater. Sci., 2008, 42, 329–336.
52. M. Torrent, F. Jollet, F. Bottin, G. Zérah and X. Gonze, Comput. Mater. Sci., 2008, 42, 337–351.
53. V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954.
54. A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467–R5470.
55. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
56. P. Nugent, T. Pham, K. McLaughlin, P. A. Georgiev, W. Lohstroh, J. P. Embs, M. J. Zaworotko, B. Space and J. Eckert, J. Mater. Chem. A, 2014, 2, 13884.
57. K. A. Forrest, T. Pham, P. A. Georgiev, F. Pinzan, C. R. Cioce, T. Unruh, J. Eckert and B. Space, Langmuir, 2015, 31, 7328–7336.
58. P. A. Georgiev, A. Albinati, B. L. Mojet, J. Ollivier and J. Eckert, J. Am. Chem. Soc., 2007, 129, 8086–8087.
59. P. D. C. Dietzel, P. A. Georgiev, J. Eckert, R. Blom, T. Strässle and T. Unruh, Chem. Commun., 2010, 46, 4962–4964.
60. T. Pham, K. A. Forrest, P. A. Georgiev, W. Lohstroh, D.-X. Xue, A. Hogan, M. Eddaoudi, B. Space and J. Eckert, Chem. Commun., 2014, 50, 14109–14112.
61. P. A. Georgiev, D. K. Ross, P. Albers and A. J. Ramirez-Cuesta, Carbon, 2006, 44, 2724–2738.
62. G. J. Kubas, Chem. Rev., 2007, 107, 4152–4205.
63. P. A. Georgiev, A. Albinati and J. Eckert, Chem. Phys. Lett., 2007, 449, 182–185.
64. T. Unruh, J. Neuhaus and W. Petry, Nucl. Instrum. Methods Phys. Res., Sect. A, 2007, 580, 1414–1422.

---

Footnotes

† Dedicated to Professor Joachim Sieler on the occasion of his 80th birthday.

‡ Electronic supplementary information (ESI) available: MOF synthesis details, single crystal and powder diffraction structure data, coordination modes of the Cu²⁺ ions, temperature dependent powder diffraction patterns, results of DFT calculations. CCDC 1922322–1922325 and 1949910. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9ce00992b

---