Influence of methyl-substitution on the dynamics of the C–H⋯F–C interaction in binary adducts

Abstract

Variable-temperature single-crystal and powder X-ray diffraction (PXRD) has been used to probe the structure and dynamics of two solid adducts, viz. toluene : hexafluorobenzene (C₆H₅CH₃ : C₆F₆) and p-xylene (1,4-dimethyl benzene) : hexafluorobenzene (p-C₆H₄(CH₃)₂ : C₆F₆). A combination of PXRD patterns and differential scanning calorimetry (DSC) traces of the solid adducts reveal two solid-state phase-transitions in each adduct: at 200 K and 246 K in C₆H₅CH₃ : C₆F₆ and at 230 K and 297 K in p-C₆H₄(CH₃)₂ : C₆F₆. The crystal structures of all three solid phases in each adduct have been solved by single-crystal X-ray diffraction (SXD). The structures of both adducts are based on close-packed parallel columns of alternating methyl benzenes and hexafluorobenzene molecules packed face to face. The fundamental difference between the two adducts involves the presence or absence of rotational disorder of the methyl-substituted benzene rings. Whereas in p-xylene the presence of two methyl groups locks the orientation of the molecule with respect to the column axis in all phases, the single methyl group of toluene fails to define a unique orientation except in the lowest temperature phase III. At higher temperatures, C₆H₅CH₃ : C₆F₆ transforms to an adduct with, initially, two-fold disorder (in phase II) and then dynamic six-fold disorder that dominates the highest temperature phase (phase I). Differences in structure between the phases as a function of temperature illustrate the subtle interplay of quadrupole versus bond–dipole electrostatic interactions.

---

Introduction

An understanding of the origins and strengths of weak van der Waals interactions in covalent solids is crucial for the prediction and preparation of bespoke, or engineered organic structures.^1,2 Of particular interest to the community of crystal engineers, is the design of organic co-crystals as alternatives to salts in the development of new materials. For organic fluorine (i.e. covalently bonded as C–F), there is a general consensus that fluorine rarely forms hydrogen bonds,^3,4 leading to questions about the nature of the interaction between neighbouring C–F and H–C bonds in the solid-state, and as to whether or not such interactions can be used to design novel structures.^5,6 The need to understand this type of weak interaction has particular importance in the pharmaceutical sector, where a variety of fluorinated active pharmaceutical ingredients have been developed.⁷

The simplest organic adduct containing a molecule with many C–F bonds, and without strong hydrogen bonding is the 1 : 1 adduct of benzene (C₆H₆) and hexafluorobenzene (C₆F₆), first reported almost 60 years ago.⁸ Both C₆H₆ and C₆F₆ are liquids at room temperature, but the binary-adduct is a solid with distinct properties; the adduct melts at 25 °C; i.e. well above the melting points of the two pure materials. This molecular adduct arises because of the strong electrostatic interactions between the benzene and hexafluorobenzene molecules that constitute the solid. The structure of the lowest-temperature phase (IV) of C₆H₆ : C₆F₆ was solved in 1991,⁹ and the structures of the other three low temperature phases was reported recently.¹⁰ Structures of high-pressure phases have also been reported.¹¹ In addition to the complex with benzene, C₆F₆ is known to form a series of 1 : 1 co-crystals with various methyl-substituted benzenes : mesitylene (1,3,5-C₆H₃(CH₃)₃),^12,13 hexamethylbenzene (C₆(CH₃)₆),^14,15p-xylene (1,4-C₆H₄(CH₃)₂),¹⁶ and durene (1,2,4,5-C₆H₂(CH₃)₄).¹⁷

Our understanding of the intermolecular interactions and cohesion in these materials has changed over time. Originally, they were thought to be, so called ‘charge-transfer solids’ and that there was a donor–acceptor or π–π* bond between C₆H₆ and C₆F₆.^17–19 However, a transfer of charge and consequent molecular orbital changes are not supported by spectroscopy as the internal vibrations of the molecules in the adduct show only a small frequency shift when compared to those of the pure solids.^20,21 An alternative model explaining the stacking of alternating molecules in these 1 : 1 adducts is provided by studies of their charge distributions.^22–24 Furthermore, it has been suggested that the expressions ‘π-stacking’ or ‘π–π interactions’ to describe the interactions in solids containing aromatic rings are misleading and should no longer be used for models based on direct electrostatic interactions.²⁵ For C₆H₆, 1,4-C₆H₄(CH₃)₂, 1,3,5-C₆H₃Me₃, C₆Me₆, and C₆F₆, the symmetry of the molecules implies that the first non-vanishing electrical moment in these systems is the quadrupole moment as described previously.

In C₆H₆ : C₆F₆, stochastic jump rotations of the rings occurs about the high symmetry axes of each component at temperatures over 150 K as shown by variable temperature X-ray diffraction¹⁰ and solid-state NMR.^18,26 By contrast, the presence of three methyl groups substituted on the benzene rings hinders stochastic jump rotations as evidenced from the atomic displacement parameters;¹³ however, the methyl groups of substituted benzene derivatives are free to rotate in order to optimize more specific and local bond–dipole interactions, leading to more subtle phase transitions as seen in the mesitylene adduct.

The results from our previous work raises two specific questions: (i) how do these adducts behave as a function of temperature for the case of one or two methyl groups substituted on a benzene ring (i.e. toluene versus xylene) and (ii) how does the symmetrically substituted two methyl adduct differ from the one methyl adduct? In particular, how does the presence of a molecule with a permanent dipole (e.g. toluene) affect the crystal structures that are formed by these adducts compared to one without (e.g. p-xylene)? A detailed study of the various structures of C₆H₅CH₃ : C₆F₆ and p-C₆H₄(CH₃)₂ : C₆F₆ presented here answers these specific questions.

Results and discussion

PXRD patterns for C₆H₅CH₃ : C₆F₆ as a function of temperature are shown in Fig. 1 (and S1‡). It is immediately apparent that there are two solid-state phase transitions: phase III is observed in the PXRD patterns up to 190 K, phase II from 200 K to 230 K, and phase I from 240 K up to 280 K. PXRD patterns for p-C₆H₄(CH₃)₂ : C₆F₆ as a function of temperature are shown in Fig. 2 (and S3‡) at two different step sizes of temperature. Using a 10 K step size in temperature, only a single phase transition was apparent. However, on narrowing the step size an additional phase transition was observed just below the melting point at 300 K. This narrow phase, labelled phase I, was first seen in the single crystal measurements and led to the second set of PXRD measurements. From PXRD, phase III was observed from 100 K to 220 K, phase II from 230 K to 296 K, and phase I from 297 K to the melt. A previous study on these adducts gave transition temperatures for C₆H₅CH₃ : C₆F₆ phase III–II at 196 K, phase II–I at 242 K, with a melting point at 282 K; and for p-C₆H₄(CH₃)₂ : C₆F₆ phase III–II at 229 K with a melting point at 301 K.²⁷

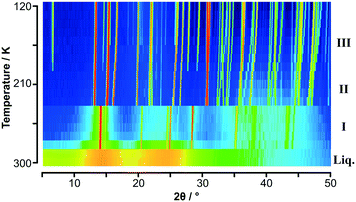Fig. 1 Variable temperature PXRD data on C₆H₅CH₃ : C₆F₆ shown as a colour surface plot. The range of intensity is shown as a spectral scale, from low counts in dark blue to high counts in red. The presence of three solid-state phases is clearly seen in addition to the “structure” seen in the molten state. Trace of solid toluene below 170 K is evident from weak peaks seen in the range 15° and 25° in 2θ (see Fig. S2‡).

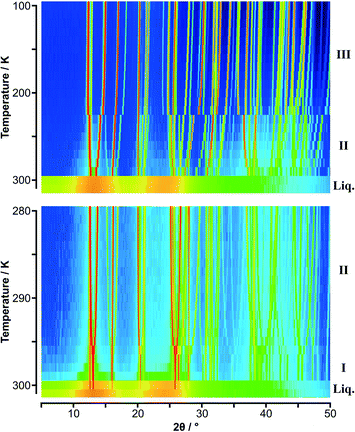Fig. 2 Variable temperature PXRD data on p-C₆H₄(CH₃)₂ : C₆F₆ shown as colour surface plots: (upper) data in 10 K steps; (lower) data in 1 K steps. The range of intensity is shown as a spectral scale, from low counts in dark blue to high counts in red. The presence of two solid-state phases is clearly seen in the data with the 10 K step; the 1 K data shows the simplification of the diffraction pattern with the formation of phase I just below the melt as seen also in Fig. S4 (lower).‡ As with C₆H₅CH₃ : C₆F₆, “structure” is seen in the molten state.

Phase transitions in both adducts were also observed by DSC, as shown in Fig. 3. For C₆H₅CH₃ : C₆F₆, the enthalpy changes on heating from phase III–II is 0.66 kJ mol⁻¹ and from phase II–I is 5.54 kJ mol⁻¹. These observed values were surprisingly reproducible (±0.01 kJ mol⁻¹) on heating and cooling for this sample: in general, DSC precision is poorer than this, and furthermore, the accuracy will be even worse due to the slight imbalance of the constituent components. For p-C₆H₄(CH₃)₂ : C₆F₆, the enthalpy changes on heating from phase III–II is 0.40 kJ mol⁻¹ and as with the toluene adduct, there is excellent agreement on both heating and cooling. As with the earlier study,²⁷ the very narrow phase I for p-C₆H₄(CH₃)₂ : C₆F₆ is not observed by our DSC measurements and a value for the enthalpy of the transition was not obtained.

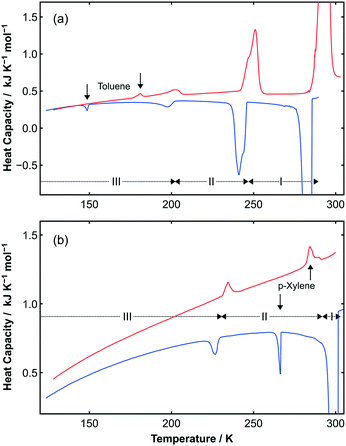Fig. 3 (a) Upper curves show DSC data obtained on cooling (blue curve) and heating (red curve) a sample of C₆H₅CH₃ : C₆F₆. Two reproducible solid-state phase transitions are observed on cooling (241 K and 198 K) and heating (202 K and 251 K). Additional peaks (as shown by vertical arrows) are observed due to the slight excess (ca. 3.5%) of toluene present in the sample due to the loss of the highly volatile C₆F₆ during sample handling. As with the DSC data for pure toluene (see Fig. S5‡), there is a noticeable hysteresis in the freezing and melting transition temperatures. (b) Lower curves show DSC data obtained on cooling (blue curve) and heating (red curve) a sample of p-C₆H₄(CH₃)₂ : C₆F₆. A reproducible solid-state phase transition is observed on cooling (227 K) and heating (234 K). Again, additional peaks (as indicated by vertical arrows) are observed, this time due to the slight excess of p-xylene present in the sample (ca. 3.6%) as indicated by the vertical arrows. The transition between phases II and I observed by X-ray diffraction are not seen due to the narrow temperature range for this transition, which is close to the melting/freezing point of the adduct. The other transitions with a large ΔH seen in the DSC are the freezing/melting transitions for the adducts.

For both adducts, hysteresis is observed in all of the phase transitions. Such hysteresis is also observed for the residual components (as shown by arrows in Fig. 3 and in S5‡). For the toluene adduct, the II–I transition displays a reproducible asymmetric peak shape. Additional PXRD measurements in 1 K steps did not reveal additional structures, although two unexplained transitory weak diffraction peaks were observed (as seen in Fig. S4‡).

For the single-crystal measurements, single crystals of the adducts were grown in situ just below the melting point by slow step-wise cooling and further annealing (see Fig. S6‡). Measurements were made starting with the highest temperature phase I of each adduct, and further measurements were made at temperatures indicated by the PXRD results. For the toluene adduct, the crystal broke into a few pieces on slow cooling into phase II (see Fig. S7‡), a behaviour similar to that observed in the benzene adduct experiments.¹⁰ Further cooling of the sample to phase III resulted in a large mosaic spread for the peaks. By contrast, the p-xylene adduct crystal twins on cooling as observed by Dahl¹⁶ and remains twinned at lower temperatures (see Fig. S8‡). Dahl reported a structure for phase II of p-C₆H₄(CH₃)₂ : C₆F₆ and the results presented here, though more precise, are in complete agreement. However, Dahl did not observe phase I and neither did he report a structure for phase III of the p-xylene adduct. No structural work has been published in the Cambridge Structural Database on the toluene adduct.

The structures of phases I, II, and III of the p-xylene adduct were solved and refined from the single-crystal data. For the toluene adduct, phases II and III were solved and refined, but for phase I only the C₆F₆ molecule could be located due to extensive dynamic disorder of the toluene moiety about the 3-fold axis in the crystal. This is in contrast to the benzene adduct where the C₆ ring of the benzene could be located in phase I as the symmetry of the molecule is commensurate with the molecular site symmetry within the crystal.¹⁰ Lattice parameters for each phase of both adducts are given in Tables 1 and 2 and views of the crystal structures are displayed in Fig. 4 and 5. The magnitude of the atomic displacements for the F atoms in C₆F₆ is about the same for both adducts at similar temperatures in contrast to the behaviour of the C atoms in the H atom containing partner.

Table 1 Lattice parameters for the three phases of C₆H₅CH₃ : C₆F₆ measured in the same sample obtained in the single-crystal experiment at the nominal temperatures quoted. Single-crystal data sets on phases II and III were also obtained at 240 K and 185 K, respectively

C6H5CH3 : C6F6	Phase I	Phase II	Phase III
T/K	260	210	150
Space group	R3̄m	I1̄	P1̄
a/Å	12.5609(13)	6.2555(12)	6.1528(7)
b/Å	12.5609(13)	13.596(2)	13.4860(12)
c/Å	7.1407(6)	7.3243(12)	7.2910(7)
α/°	90	81.725(13)	81.655(8)
β/°	90	84.578(14)	85.547(9)
γ/°	120	94.028(14)	95.194(9)
V/Z/Å^3	325.2(1)	305.7(1)	296.79(5)

---

Table 2 Lattice parameters for the three phases of p-C₆H₄(CH₃)₂ : C₆F₆ measured on the same sample obtained in the single-crystal experiment at the nominal temperatures quoted. A single-crystal data set on phase II was also obtained at 280 K

p-C6H4(CH3)2 : C6F6	Phase I	Phase II	Phase III
T/K	300	240	150
Space group	C2/m	C1̄	C1̄
a/Å	8.8690(12)	8.8550(7)	8.8241(6)
b/Å	11.0285(17)	10.9108(8)	10.8149(6)
c/Å	7.3047(10)	7.2985(6)	7.2972(5)
α/°	90	83.416(6)	80.420(5)
β/°	106.483(13)	107.852(7)	109.086(7)
γ/°	90	98.730(6)	103.477(5)
V/Z/Å^3	342.56(9)	330.84(5)	318.45(4)

---

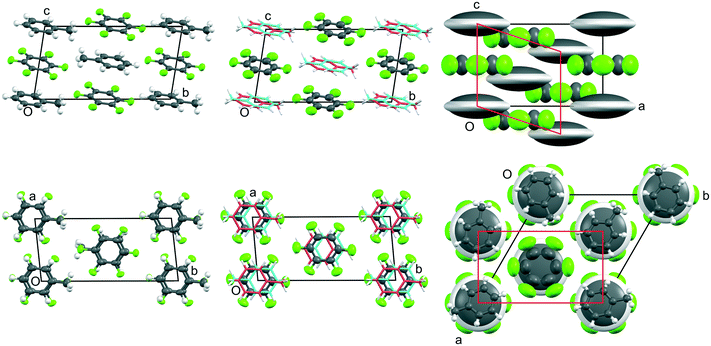Fig. 4 Views down a (top row) and -c (bottom row) of the crystal structures of phases III, II, and I (from left to right, respectively) of C₆H₅CH₃ : C₆F₆ showing the evolution of the thermal motion as a function of temperature (from data measured at 150 K, 185 K, 210 K, 235 K, and 260 K, respectively). The crystallographic labelling of the atoms in each phase is shown in Fig. S9‡ and additional views shown in Fig. S10.‡ Thermal ellipsoids are drawn at 50% probability (with H atoms at a fixed radius): for phase II, twofold disorder of the toluene molecule is shown using a stick representation with the two possible orientations coloured as deep pink or cyan; for phase I, the single giant grey and white ellipsoids represents a model of a continuously rotating toluene molecule. In order to relate the unit cells of phases II and III, a non-standard I-centred triclinic unit cell (with space group symmetry I1̄) has been chosen for phase II and a non-standard origin has been used for phase III. In the lower figure of phase I, individual toluene molecules are shown superimposed in frozen in random orientations; the average diameter is slightly smaller than that of the C₆F₆ molecule. As for the benzene adduct, the cell shown in red is a monoclinic cell derived from the rhombohedral cell used for phase I, and which relates to phase II as discussed in the ESI.‡

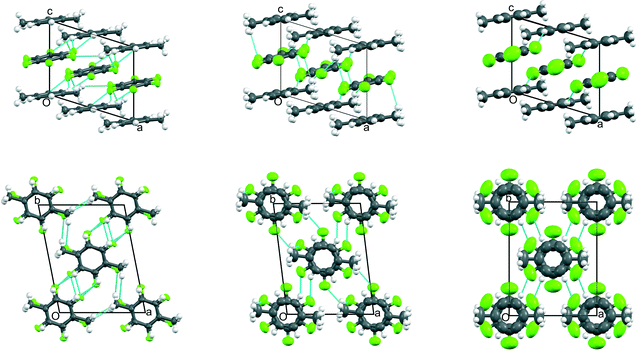Fig. 5 Views down -b (top row) and c (bottom row) of the crystal structures of phases III, II, and I (from left to right, respectively) of p-C₆H₄(CH₃)₂ : C₆F₆ showing the evolution of the thermal motion as a function of temperature (from data measured at 150 K, 240 K, and 300 K, respectively). The crystallographic labelling of the atoms in each phase is shown in Fig. S11 and additional views shown in Fig. S12.‡ Thermal ellipsoids are drawn at 50% probability (with H atoms at a fixed radius). In order to relate the unit cells for phases I to III, a non-standard C-centred triclinic unit cell (with space group symmetry C1̄) has been chosen for phases II and III. The shortest C–F⋯H–C distances (<2.9 Å) are shown in cyan.

Using the unit cells from the solved structures of each phase, Le Bail fits to the PXRD data were made to obtain the temperature dependence of the lattice parameters for both adducts. The change in volume with temperature is shown in Fig. 6; the corresponding changes in cell lengths and angles are shown in Fig. S13 and S14.‡ Values are given in Tables 7a and b in the ESI.‡ It is immediately apparent from the figure that for the toluene adduct there is a large volume change between phase I and II, which accounts for the crystals breaking on cooling. By contrast, the smooth continuous volume change for the p-xylene adduct is consistent with the observation of crystal stability down to low temperature.

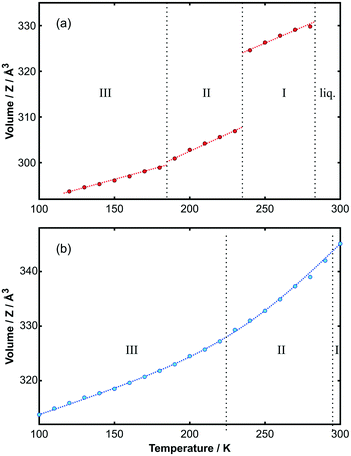Fig. 6 Volume per unit of (a) C₆H₅CH₃ : C₆F₆ and (b) p-C₆H₄(CH₃)₂ : C₆F₆ as a function of temperature. The discontinuity in the toluene adduct represents a volume change of 5.5% at the transition temperature. Phase boundaries are provided by vertical dotted lines. The curve through the points is a guide to the eye. The variation of individual unit-cell parameters with temperature is shown in Fig. S13 and S14‡ for each adduct, respectively. Further details are provided in the ESI.‡

The variable temperature study of the two adducts C₆H₅CH₃ : C₆F₆ and p-C₆H₄(CH₃)₂ : C₆F₆ permits a comparison of the dynamics of closely-related species; in particular, of the influence of methyl groups on the stability of the solid adduct. For the pair of adducts studied here, toluene has a small permanent electric dipole moment (0.33 D),²⁸ whereas p-xylene has two C–CH₃ dipole moments that are opposed and cancel. However, there remains the question of the different size of the molecules and how this influences the dynamics of the solid.

The high-temperature phase of C₆H₅CH₃ : C₆F₆ shows similar structure and dynamics to that observed in C₆H₆ : C₆F₆.¹⁰ Both adducts exhibit space-group symmetry R3̄m in their highest temperature phases, with each molecule on a site of 3̄m symmetry. In the benzene adduct, which is the prototype for this whole class of materials, the dynamics of the benzene is readily modelled in terms of near free rotation around the 6-fold molecular axis in phase I using multiple ellipsoids (and using large ellipsoids in phase II) for the C and H atoms. At these temperatures in the benzene adduct, the C₆F₆ molecule remains in a fixed position despite large angular librations as evidenced by the atomic displacement parameters. In the toluene adduct, the addition of a methyl group to the C₆-ring breaks the inversion symmetry of the molecule so that the centre of mass is no longer at the centre of the ring. Given the 3̄m molecular site symmetry (see Fig. S9‡), the –CH₃ group must be dynamically disordered over 6 possible sites with the normal to the C₆-ring no longer coaxial with the 3-fold crystal axis. Consequently, with only 42 unique reflections, there is a severe limitation on the complexity of the model designed to try and fit the data, in contrast to the benzene adduct where the centre of mass of C₆H₆ is always on the 3-fold axis. Using the “squeeze” technique, the position of the C₆F₆ moiety can be refined but the coordinates for the dynamically disordered-toluene molecule cannot be determined or refined.

On cooling, the 6-fold dynamic disorder of phase I of C₆H₅CH₃ : C₆F₆ transforms to 2-fold dynamic disorder with the permanent dipole moments aligned in a parallel or antiparallel manner demonstrating the flatness of the electrostatic potentials provided by the adjacent C₆F₆ molecules within a column. On further cooling to phase III, the 2-fold disorder is lost and the structure adopts an antiferroelectric arrangement of the permanent dipoles as seen schematically in Fig. 4. The dynamic nature of these order–disorder transitions may be seen from the temperature dependence of the intensity of the non-I-centred reflections (i.e. with hkl: h + k + l ≠ 2n) in phase III (see Fig. S15‡). Further evidence for dynamic disorder is given by SXD data on phase III measured at 185 K: the best fit to the data at this temperature without disorder has R₁ equal to 10.15% but this reduces to 6.04% for a model with 16.7% toluene disorder.

From a symmetry perspective, although the space-group symmetry of both phases II and III is the same, i.e. centrosymmetric triclinic (space group no. 2), the phase transformation involves a symmetry change from black–white (two different orientations) in phase III to grey (an average of the two orientations) in phase II,²⁹ and so can be considered in terms of the 2-D Ising model used to describe certain magnetic phase transitions. Although a reduced temperature τ = (T − T_C)/T_C can be calculated readily given the II–III transition temperature T_C, the order parameter Ψ cannot be easily derived from peak-intensity data (as shown in Fig. S15‡), thus limiting critical-behaviour analysis using the PXRD data.

In the p-xylene adduct, the presence of a second methyl group symmetrically disposed to the first prevents rotational disorder of the hydrogen-containing ring, even at the highest temperatures. Our previous work on 1,3,5-C₆H₃(CH₃)₃ : C₆F₆ also demonstrated that a symmetrical arrangement of methyl groups precluded disorder of the C₆-ring,¹³ though it does not prevent disorder of the methyl groups at higher temperatures when the inter-column electrostatic interactions diminish. The isosymmetric transition between phases III and II in p-C₆H₄(CH₃)₂ : C₆F₆ can be explained in terms of order–disorder transitions involving the methyl group interactions with fluorine atoms in neighbouring columns, as observed in the mesitylene adduct. Although the space-group symmetry of both phases II and III is the same, i.e. centrosymmetric triclinic (space group no. 2), this transition differs significantly from the II–III transition observed in C₆H₅CH₃ : C₆F₆. The phase transition involves a slight rotation of the p-xylene molecule from eclipsed (with respect to the C₆F₆ ring) in phase III to partially staggered in phase II, and is classed as type 0 in symmetry terms.³⁰ From the lattice parameters derived from the PXRD data (see Fig. S14‡), it is clear that this isosymmetric transition is discontinuous in contrast to some others of this type.³¹

The transition between phases II and I of p-C₆H₄(CH₃)₂ : C₆F₆ involves a further rotation of the p-xylene moiety relative to the C₆F₆ molecule so that molecules become perfectly staggered in phase I with point symmetry 2/m (see Fig. S11‡). However, this staggered structure is unstable with respect to change of temperature due to lack of inter-columnar interactions; hence the narrowness of this phase.

On the subject of inter-columnar interactions, it is now possible to give inter-column distance values for a range of closely-related adducts in their highest temperature phases: 6.93 Å in C₆H₆ : C₆F₆ (at 285 K); 7.25 Å in C₆H₅CH₃ : C₆F₆ (at 260 K); 6.96 Å in p-C₆H₄(CH₃)₂ : C₆F₆ (at 300 K); and 7.13 Å in 1,3,5-C₆H₃(CH₃)₃ : C₆F₆ (at 190 K). For the benzene and toluene adducts, the columns are close-packed and there is a single inter-column spacing; for p-xylene adduct the value is for the nearest neighbour spacing where the methyl groups are not opposed; and for the mesitylene adduct the value corresponds to the nearest neighbour spacing with no methyl groups interposed. These values reveal something of the nature of the inter-columnar interactions in these closely-related adducts. For the benzene adduct, the columns are the most closely packed despite dynamic disorder existing in phases I and II which suggests that the inter-columnar spacing is determined mainly by the interactions of the larger C₆F₆ molecules in neighbouring columns. In the p-xylene adduct, the spacing is only marginally greater, but in the toluene adduct it is significantly larger than the spacing in the benzene adduct. This larger separation of the columns means that electrostatic interactions between neighbouring columns will be significantly weaker for the toluene adduct; e.g. for dipole–dipole interactions the interaction energy varies as 1/r³ where r is the spacing between the dipoles.³² Consequently, it is perhaps not so surprising that there is so much disorder in the toluene adduct.

Perhaps the biggest difference between the two systems presented here and the structure of the lowest temperature phase IV of C₆H₆ : C₆F₆ is that the bond dipoles on both the toluene and p-xylene molecules and those on their C₆F₆ neighbours in a column are perfectly eclipsed (as seen in Fig. 4 and 5). By contrast, in phase IV of C₆H₆ : C₆F₆, the C–H bond dipoles in the C₆H₆ molecule and the C–F bond dipoles in the C₆F₆ molecules both above and below it are neither eclipsed nor staggered, but at an angle of around 18° between the axis of the C–H bond and a paired C–F bond when viewed down the c-axis.^9,10 On heating p-C₆H₄(CH₃)₂ : C₆F₆, the transition from phase III to phase II results in a relative rotation of the two component molecules such that a partially staggered structured is obtained, and this relative rotation continues into phase I where the molecules are perfectly staggered. By contrast, heating C₆H₅CH₃ : C₆F₆ from phase III to phase II leaves the molecules eclipsed, though no comment can be made about the relative orientation of the molecules on further heating to phase I.

This difference between the relative orientations at low temperature of the toluene and p-xylene molecules with respect to C₆F₆ molecules in the same column when compared with the relative orientation of benzene in these adducts is due to the relative magnitudes of the intermolecular electrostatic-potential between the columns of alternating molecules and the electrostatic potential within a column in these binary adducts. The inter-columnar potential and the intra-columnar potential will be similar for all three binary-adducts, but there will be differences. The lowest-energy configuration of the bond dipoles in these binary-adduct is the eclipsed geometry. This geometry maximises the bond–dipole – bond–dipole interaction of the parallel molecules, which then contributes to the intra-columnar potential. In addition, the presence of the methyl group (s) in toluene and p-xylene provides an additional bond–dipole electrostatic interaction to contribute to the intra-columnar potential.

However, if the columns of molecules are close together, then the interaction of the molecules in a column will be perturbed by the close proximity of molecules (bond–dipole moments) in neighbouring columns. In all of this series of adducts, this perturbation results in a tilt of the molecules with respect to the column axis as commented on previously.^10,13 In addition, a strong inter-columnar perturbation can generate a structure within a column that is neither eclipsed, nor completely staggered, as seen in phase IV of C₆H₆ : C₆F₆, but that is not seen in the toluene and p-xylene adducts at low temperature. On heating to phase III of C₆H₆ : C₆F₆ (in which the columns of molecules are more separated), the intra-columnar interactions become more important for the crystal structure than the inter-columnar term and the C–F and C–H bond dipoles become eclipsed as in C₆H₅CH₃ : C₆F₆ and p-C₆H₄(CH₃)₂ : C₆F₆.

The effect of these competing interactions in these adducts can also be seen in deviations from the parallel behaviour of the C₆F₆ and methyl-substituted benzene rings with temperature. For the parent adduct C₆H₆ : C₆F₆, the two constituent molecules are perfectly co-planar in phase I but tilt relative to each other by 3.5° in phase II, 4.6° in phase III, and 5.2° in phase IV. Similarly, in the toluene adduct, the relative tilt is 0° in phase I and increases to 3.7° in phase III. By contrast, in the p-xylene adduct, the two molecules are not co-planar in any of the solid phases and the relative tilt varies only slightly from 5.8° in phase III (as shown e.g. in Fig. S16‡) to 5.5° in phase I. For comparison, the relative tilt between the constituent molecules in the mesitylene adduct increases on cooling from 1.1° in phase I to 1.9° in phase II, and then to a range of tilts in phase III (since Z′ > 1).

Finally, it is worth noting that in their pure form, both toluene and p-xylene are liquids at room temperature: toluene melts at 179 K and boils at 384 K, giving it one of the largest liquid-ranges of any small molecule; p-xylene melts at 286 K and boils at 411 K. By forming a binary-adduct (or co-crystal) with C₆F₆, where structural integrity is maintained by electrostatic interactions involving bond–dipole moments on the two components, toluene may be retained in an ordered form up to almost 280 K in a toluene adduct and p-xylene in a solid ordered form up to almost 300 K in its adduct. This marked difference in behaviour in the presence of hexafluorobenzene explains the keen interest in the use of perfluoroaromatic compounds in crystal engineering,³³e.g. in the stabilization of graphene sheets,³⁴ and in the self-assembly of bespoke cocrystals with tuneable luminescence colour.³⁵

Experimental

Samples were prepared by mixing the components in a 1 : 1 molar ratio. DSC measurements were made using a liquid N₂ cooled PerkinElmer DSC8000 with a base temperature of 93 K. Variable temperature laboratory PXRD measurements were made using a Stoe Stadi-P diffractometer. SXD data sets were obtained on an Agilent SuperNova diffractometer. Further details of all experiments are available in the ESI.‡

Conclusions

This paper is part of a series on the use of engineered crystal structures to study intermolecular interactions and their influence on crystal structure. Variable-temperature single-crystal and powder X-ray diffraction has been used to probe the structure and dynamics of the two solid adducts C₆H₅CH₃ : C₆F₆ and p-C₆H₄(CH₃)₂ : C₆F₆, each of which has two solid-state phase-transitions. The structures of all three solid phases in each adduct have been solved. This analysis reveals a good deal about the possible use of binary-adducts in crystal engineering. Our previous work focussed on the prototypical binary-adduct C₆H₆ : C₆F₆ and the adduct formed by the non-polar trimethyl-substituted derivative of benzene, 1,3,5-C₆H₃(CH₃)₃ : C₆F₆. This series of papers demonstrates how to introduce, control, and eliminate disorder in bespoke solids by the introduction or elimination of methyl groups attached to the major structural elements of the solid.

In addition, this work demonstrates the importance of using finer steps for variable temperature PXRD studies of phase transitions in these materials. There is a risk of not observing phases that exist over a narrow range of temperature using 10 K measurement steps; though the finer probe of 1 K steps may reveal more, it is not always practical to do this in an X-ray laboratory with restricted access time.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge financial support from the EPSRC for funding the single-crystal and powder X-ray diffractometers (grant reference EP/K03930X/1). We thank Dr. Alexander Rosu-Finsen and Prof. Christoph G. Salzmann for use of their DSC calorimeter. We are particularly grateful to Dr. Ronen E. Ghosh for his help in developing in-house software to automate the collection of variable temperature PXRD data using the Oxford Instrument CryojetHT on the Stoe Stadi-P diffractometer. We thank Prof. Andrew S. Wills for useful discussions.

References

1. J. D. Dunitz and A. Gavezzotti, Chem. Soc. Rev., 2009, 38, 2622–2633.
2. G. R. Desiraju, J. Am. Chem. Soc., 2013, 135, 9952–9967.
3. P. Panini and D. Chopra, in Hydrogen Bonded Supramolecular Structures, ed. Z. Li and L. Wu, Lecture Notes in Chemistry, Springer-Verlag, 2015, ch. 2, vol. 87, pp. 37–67.
4. A. Gavezzotti and L. L. Presti, Cryst. Growth Des., 2016, 16, 2952–2962.
5. J. A. K. Howard, V. J. Hoy, D. O'Hagan and G. T. Smith, Tetrahedron, 1996, 52, 12613–12622.
6. V. R. Thalladi, H.-C. Weiss, D. Bläser, R. Boese, A. Nangia and G. R. Desiraju, J. Am. Chem. Soc., 1998, 120, 8702–8710.
7. K. Müller, C. Faeh and F. Diederich, Science, 2007, 317, 1881–1886.
8. C. R. Patrick and G. S. Prosser, Nature, 1960, 187, 1021.
9. J. H. Williams, J. K. Cockcroft and A. N. Fitch, Angew. Chem., Int. Ed. Engl., 1992, 31, 1655–1657.
10. J. K. Cockcroft, A. Rosu-Finsen, A. N. Fitch and J. H. Williams, CrystEngComm, 2018, 20, 6677–6682.
11. Y. Wang, L. Wang, H. Zheng, K. Li, M. Andrzejewski, T. Hattori, A. Sano-Furukawa, A. Katrusiak, Y. Meng, F. Liao, F. Hong and H. Mao, J. Phys. Chem. C, 2016, 120, 29510–29519.
12. T. Dahl, Acta Chem. Scand., 1971, 25, 1031–1039.
13. J. K. Cockcroft, R. E. Ghosh, J. J. Shephard, A. Singh and J. H. Williams, CrystEngComm, 2017, 19, 1019–1023.
14. T. Dahl, Acta Chem. Scand., 1972, 26, 1569–1575.
15. T. Dahl, Acta Chem. Scand., 1973, 27, 995–1003.
16. T. Dahl, Acta Chem. Scand., Ser. A, 1975, 29, 170–174.
17. T. Dahl, Acta Chem. Scand., Ser. A, 1975, 29, 699–705.
18. D. F. R. Gilson and C. A. McDowell, Can. J. Chem., 1966, 44, 945–952.
19. T. Dahl, Acta Chem. Scand., Ser. A, 1988, 42, 1–7.
20. J. H. Williams, Mol. Phys., 1991, 73, 99–112.
21. J. H. Williams, Chem. Phys., 1993, 172, 171–186.
22. N. M. D. Brown and F. L. Swinton, J. Chem. Soc., Chem. Commun., 1974, 770–771.
23. J. Hernandez-Trujillo, M. Costas and A. Vela, J. Chem. Soc., Faraday Trans., 1993, 89, 2441–2443.
24. J. H. Williams, Acc. Chem. Res., 1993, 26, 593–598.
25. C. R. Martinez and B. L. Iverson, Chem. Sci., 2012, 3, 2191–2201.
26. M. J. Duer, J. Chem. Soc., Faraday Trans., 1993, 89, 823–826.
27. D. Mikailitchenko, A. Marbeuf, Y. Haget and H. A. J. Oonk, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1998, 319, 291–305.
28. C. W. N. Cumper, A. Melnikoff and R. F. Rossiter, Trans. Faraday Soc., 1969, 65, 2892–2899.
29. A. S. Wills, Powder Diffr., 2017, 32, 148–155.
30. A. G. Christy, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 1995, 51, 753–757.
31. J. K. Cockcroft, Ph.D. Thesis, University of Oxford, 1985; I. P. Swainson, R. P. Hammond, J. K. Cockcroft and R. D. Weir, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 174109 (5pp).
32. A. D. Buckingham, Adv. Chem. Phys., 1967, 12, 107–142.
33. S. Bhandary and D. Chopra, Cryst. Growth Des., 2018, 18, 3027–3036.
34. A. J. Oyer, J.-M. Y. Carrillo, C. C. Hire, H. C. Schniepp, A. D. Asandei, A. V. Dobrynin and D. H. Adamson, J. Am. Chem. Soc., 2012, 134, 5018–5021.
35. L. Li, Z. F. Liu, W. X. Wu and W. J. Jin, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2018, 74, 610–617.

---

Footnotes

† This paper is dedicated to Sir Brian E. F. Fender CMG on the occasion of his 85th birthday.

‡ Electronic supplementary information (ESI) available: Additional experimental detail, crystallographic tables, and additional supporting figures are supplied. CCDC CIF files have been deposited at Cambridge Crystallographic Data Center for C₆H₅CH₃ : C₆F₆ with deposition numbers 1908707 (phase I at 260 K), 1908706 (phase II at 235 K), 1908705 (phase II at 210 K), 1908704 (phase III at 185 K), and 1908703 (phase III at 150 K) and for p-C₆H₄(CH₃)₂ : C₆F₆ with deposition numbers 1908128 (phase I at 300 K), 1908127 (phase II at 280 K), 1908126 (phase II at 240 K), and 1908125 (phase III at 150 K). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9ce00541b

§ Retired. Current address: Montpellier, France. E-mail: E-mail: jeffreyhuw@hotmail.com

---