Probing non-covalent interactions driving molecular assembly in organo-electronic building blocks†
Sarah N.
Johnson
 a,
Thomas L.
Ellington
a,
Thomas L.
Ellington
 a,
Duong T.
Ngo
a,
Jorge L.
Nevarez
a,
Nicholas
Sparks
a,
Arnold L.
Rheingold
b,
Davita L.
Watkins
a,
Duong T.
Ngo
a,
Jorge L.
Nevarez
a,
Nicholas
Sparks
a,
Arnold L.
Rheingold
b,
Davita L.
Watkins
 *a and
Gregory S.
Tschumper
*a and
Gregory S.
Tschumper
 *a
*a
aDepartment of Chemistry and Biochemistry, University of Mississippi, University, Mississippi 38677-1848, USA. E-mail: tschumpr@olemiss.edu; Fax: +1 662 915 7300; Tel: +1 662 915 7301
bDepartment of Chemistry, University of California, San Diego, La Jolla, California 92093-0358, USA
First published on 14th March 2019
Abstract
Recent advancements in material science exploit non-covalent interactions, such as halogen bonding (XB) or π-stacking within solid-state molecular frameworks for application in organic electronic devices. Herein, we focus on these and other non-covalent interactions and the effect that furan and thiophene substituents play on the solid-state properties of co-crystals formed between pentafluoro(iodoethynyl)benzene (F5BAI; XB donor) and a pyridine disubstituted with either furans or thiophenes (PyrFur2 and PyrThio2; XB acceptors). Spectroscopic and thermal analyses of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures provide indirect evidence of XB interactions, whereas X-ray crystallography provides direct evidence that XB and π-stacking are present in both co-crystals. Density functional theory (DFT) computations provide insight into the relative electronic energetics of each pair-wise contact observed in the experimental F5BAI-PyrFur2 and F5BAI-PyrThio2 co-crystals.
1 mixtures provide indirect evidence of XB interactions, whereas X-ray crystallography provides direct evidence that XB and π-stacking are present in both co-crystals. Density functional theory (DFT) computations provide insight into the relative electronic energetics of each pair-wise contact observed in the experimental F5BAI-PyrFur2 and F5BAI-PyrThio2 co-crystals.
1 Introduction
Crystal engineering and material science studies have recently emerged placing particular emphasis on the utilization of non-covalent interactions, such as hydrogen bonding and/or π-stacking, as a tool to control molecular assembly on the nanoscale level.1–11 Efficient organic optoelectronic devices, such as organic light-emitting diodes (OLEDs) or organic field-effect transistors (OFETs), often possess large optical and fundamental energy gaps between their ground and excited state structures.12–21 These molecular properties have been most extensively investigated in the solid-state, where emphasis is placed on intramolecular and intermolecular charge or electron density transfer, via molecular orbital overlap. Of particular interest is the incorporation of similar non-covalent interactions in the design of molecular building blocks suitable for use in organic optoelectronic devices.The incorporation of halogen bonding as an intermolecular interaction is ever-growing throughout the literature.22–24 As formally defined by the International Union of Pure and Applied Chemistry (IUPAC), a halogen bond (XB) is a net attractive interaction between an electrophilic region associated with a halogen atom in a molecular entity and a nucleophilic region in another, or the same molecular entity.25 The formation of such an interaction occurs due to the anisotropic redistribution of electron density upon the formation of a covalent bond between the halogen atom (X) and a neighboring atom (C–X).26–29 This polarization can produce a region of depleted electron density that is aligned with the C–X bond (i.e., the σ-hole).28–30 These areas can have a positive electrostatic potential allowing for the formation of an attractive and highly directional intermolecular interaction with a nucleophilie whose magnitude is on order with a typical hydrogen bond (ca. 5 kcal mol−1).27,31 Here we use the term “XB” to describe the attractive interaction between the σ-hole of a halogen-containing molecule (XB donor) and an electron rich region of a neighboring Lewis base (XB acceptor), typically in the form of the lone pair(s) from a pnicogen or chalcogen atom.25 In addition to the inherent strength and directionality of these interactions, the XB can be tuned via modification of (i) the halogen atoms polarizability through its identity (I > Br > Cl ≫ F) and/or (ii) electron withdrawing ability of the XB donor, which makes the XB a powerful addition to crystal growth and design.31–33 Perhaps most important is the overarching idea that the distribution of electron density across the entire XB complex plays a pivotal role when investigating solid-state molecular assemblies.22,34
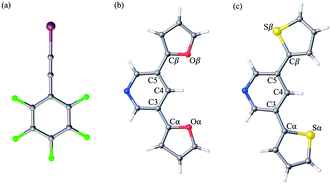
Herein, we report the analysis of single crystal structural data for a series of co-crystals comprised of self-assembling optoelectronic building blocks and an iodoethynyl benzene derivative. Fig. 1 shows the chemical structure of the three molecules of study. Initially prepared as oligomeric moieties for the construction of single crystal organic semiconducting devices, the truncated pyridine-based derivatives (PyrFur2 and PyrThio2) were employed as XB acceptors. The core nitrogen containing heterocycle (Pyr) acts as a synthetically accessible Lewis base capable of donating electrons to the XB complexation. The furan (Fur) and thiophene (Thio) units represent traditional building blocks used in material science.35 Based on semiconducting properties, thiophene is widely accepted as a better electron donor while furan has been reported to yield more planar geometries due to the reduced size of the oxygen atom in comparison to that of the sulfur.36 The effects of the structural diversity lead to uniquely different chemical and physical properties that are often varied depending on solid-state arrangement.37,38
The well established XB donor, 1,2,3,4,5-pentafluoro(iodoethynyl)benzene (F5BAI, i.e. F5C8I) contains a highly polarizable iodine atom with a significant region of positive electrostatic potential on the outermost portion of its surface.30,39 The capacity for XBing at the iodine atom is enhanced by the sp hybridization of the adjacent carbon (i.e., C–I) as well as an inductive effect provided by the fluoro substituents.40 Together the components that make up the XB acceptor and donor induce self-assembly yielding highly directional XB complexes which also stack via π-type interactions. As suggested in the naming scheme, the F5BAI-PyrFur2 co-crystal contains the PyrFur2 XB acceptor (i.e. NO2C13H9), while F5BAI-PyrThio2 contains the PyrThio2 XB acceptor (i.e. NS2C13H9). In order to quantify the planarity for the furan and thiophene substituents within the PyrFur2 and PyrThio2 XB acceptors, two torsional angles τα and τβ are defined by the atom labels C4–C3–Cα–Yα and C4–C5–Cβ–Yβ, respectively, in Fig. 1 where Y is either O or S. Nearest neighbor pair-wise intermolecular interactions identified in the two co-crystals via X-ray crystallography are quantified with the application of density functional theory (DFT) computations.
2 Methods and materials
Reagents and solvents were purchased from commercial sources and used without further purification unless otherwise specified. Infrared (IR) spectra were recorded with an Agilent Cary 660 ATR-FTIR. A Fisher-Johns melting point apparatus was used to determine melting points. Additional synthetic details, summary of theoretical calculations, structural figures, TG/DTZ plots, and X-ray crystallographic tables containing bond distances and angles can be found in the (ESI†).2.1 Thermogravimetric analysis
Measurements were performed on Seiko Instruments TG/DTZ 6200 (platinum pan, room temperature to 550 °C, ramp rate of 20 °C min−1 under nitrogen atmosphere) and analyzed on TG/DTZ Highway Conversion Software.2.2 X-ray crystallography
Crystal evaluation and data collection were performed on a Bruker Kappa diffractometer with Mo Kα (λ = 0.71073 Å) radiation. Reflections were indexed by an automated indexing routine built in the APEXII program suite. The solution and refinement were carried out in Olex2 version 1.2 using the program SHELXTL.41,42 Non-hydrogen atoms were refined with anisotropic thermal parameters while hydrogen atoms were introduced at calculated positions based on their carrier/parent atoms. Crystal data and structure refinement parameters for all compounds are given in the ESI.† The single crystal X-ray structure of the co-crystal CCDC numbers are [1876245 and 1876246].2.3 Computational methods
The global hybrid M06-2X43 density functional was employed in conjunction with a triple-ζ correlation consistent basis set augmented with diffuse functions on all atoms and a relativistic pseudopotential on iodine centers (aug-cc-pVTZ-PP)44–47 in order to compute the electronic interaction energies (Eint) of all nearest neighbor contacts in the experimental crystal structures. This effectively corresponds to a distance threshold for pair-wise contacts having any atomic centers within 5 Å of each other. The M06-2X density functional was employed in the current study because it has been extensively calibrated and shown to provide reasonably accurate energies for a wide range of non-covalent interactions,48 including halogen bonds.49 The interaction energies were calculated by comparing the electronic energy of fragment pairs from the crystal structure to the electronic energies of the corresponding isolated fragments (also at their corresponding crystal structure geometries). All interaction energies were computed with and without the Boys–Bernardi counterpoise procedure50,51 in order to account for basis set superposition error52,53 following a procedure for non-covalent clusters with rigid fragments described in detail elsewhere.54 All computations were performed with the Gaussian09 software package55 using atomic coordinates obtained from the X-ray crystal structures. The interaction energies, Cartesian coordinates and figures for all contacts are provided in the ESI.†3 Results and discussion
3.1 Preliminary investigations and crystal growth
XB acceptors and donors were synthesized and co-crystallized according to modified literature procedures.22 Co-crystals, F5BAI-PyrFur2 and F5BAI-PyrThio2 were prepared in duplicate at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio by dissolving each XB acceptor separately in a chlorinated solvent (dichloromethane or chloroform) and adding it to a borosilicate glass vial containing the XB donor. The resulting mixtures were ultrasonicated for 10 minutes. The open vial was placed in a secondary vial containing a more volatile solvent (n-hexane, n-pentane or methanol). The solvents were paired according to the following combinations: dichloromethane–pentane; chloroform–methanol; chloroform–hexane. Using vapor diffusion methods, the solvent was allowed to completely evaporate at −10 °C over 7 days until the formation of crystals occurred. Confirmation of co-crystallization was observed through a ≥40 °C difference in melting point between the co-crystals and the XB acceptors (Table S1 and Fig. S2–S4†).56,57 Additionally, the co-crystals were analyzed using IR spectroscopy (Table S1 and Fig. S1†), in order to indirectly confirm successful formation of XB interactions by identifying the C
1 ratio by dissolving each XB acceptor separately in a chlorinated solvent (dichloromethane or chloroform) and adding it to a borosilicate glass vial containing the XB donor. The resulting mixtures were ultrasonicated for 10 minutes. The open vial was placed in a secondary vial containing a more volatile solvent (n-hexane, n-pentane or methanol). The solvents were paired according to the following combinations: dichloromethane–pentane; chloroform–methanol; chloroform–hexane. Using vapor diffusion methods, the solvent was allowed to completely evaporate at −10 °C over 7 days until the formation of crystals occurred. Confirmation of co-crystallization was observed through a ≥40 °C difference in melting point between the co-crystals and the XB acceptors (Table S1 and Fig. S2–S4†).56,57 Additionally, the co-crystals were analyzed using IR spectroscopy (Table S1 and Fig. S1†), in order to indirectly confirm successful formation of XB interactions by identifying the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C triple bond peak of the complex compared to that of the XB donor F5BAI.
C triple bond peak of the complex compared to that of the XB donor F5BAI.
Further analysis of the thermogravimetric (TGA) data for the co-crystals reveals dual step decomposition patterns indicating the presence of two complex species (Fig. S3†). Similar trends are observed for neat XB acceptors and co-crystals where furan-based materials have lower decomposition temperatures than those consisting of thiophene. This is an innate property of the material that has been well documented in the literature.58,59 Notably, the decomposition temperatures for each co-crystal are within 52–97 °C lower than those observed for each neat XB acceptor. F5BAI-PyrFur2 and F5BAI-PyrThio2 exhibit initial decomposition temperatures of 107 °C and 111 °C, respectively. These results indicate that the interactions within the neat XB acceptors are presumed to be much stronger than those within the XB complexes.
3.2 Crystal structure analyses
Single crystal X-ray data was utilized to elucidate the nature of the XB and other non-covalent interactions within the resulting co-crystals. A summary of the crystallographic data is provided in Table 1. A 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 assembly of F5BAI-PyrFur2 yields co-crystallization in the triclinic space group P
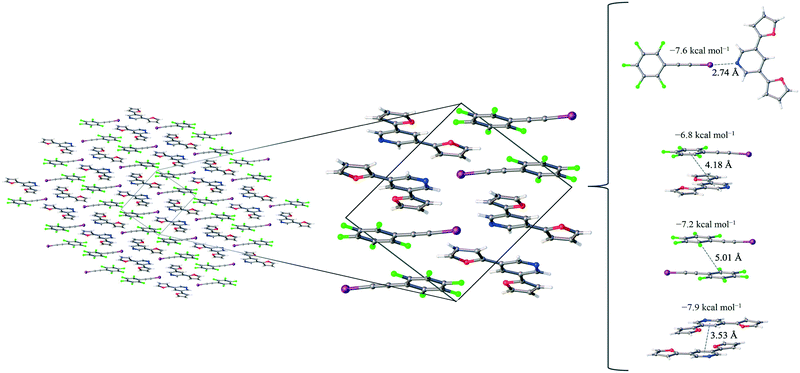
1 assembly of F5BAI-PyrFur2 yields co-crystallization in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , where the dimers pack antiparallel to each other along the c-axis (Fig. 2).
, where the dimers pack antiparallel to each other along the c-axis (Fig. 2).
| Co-crystal | F 5 BAI-PyrFur 2 | F 5 BAI-PyrThio 2 |
|---|---|---|
| Formula | C21H9F5INO2 | C21H9F5INS2 |
| M (g mol−1) | 529.2 | 561.3 |
| Temperature (K) | 200.0 | 100.0 |
| Space group |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P21/c |
| a (Å) | 8.698(15) | 11.921(3) |
| b (Å) | 10.499(15) | 16.418(4) |
| c (Å) | 12.215(2) | 10.642(2) |
| α (°) | 86.92 | 90.00 |
| β (°) | 70.76 | 104.41 |
| γ (°) | 68.53 | 90.00 |
| V (Å3) | 977.2 | 2017.3 |
| Z | 2 | 4 |
| R factor (%) | 3.81 | 2.34 |
The only configuration of PyrFur2 observed in the co-crystal structure is almost perfectly planar with magnitudes of τα and τβ (depicted in Fig. 1) falling near 3°, which indicates both chalcogens have adopted orientations away from the nitrogen atom of the central pyridine ring as seen throughout Fig. 2. Full geometry optimizations at the M06-2X/aug-cc-pVTZ-PP level of theory indicate several different configurations of PyrFur2 have similar electronic energies (reported in the ESI†). A Cs configuration with τα = 0° and τβ = 180° lies only +0.15 kcal mol−1 above the C2v configuration with τα and τβ = 0°. The XB interaction between the pyridyl nitrogen and iodine atoms is characterized by a nearly linear N⋯I–C angle of 175° and a N⋯I distance (2.74 Å) that is 34.3% less than the sum of their van der Waals radii of nitrogen (1.79 Å) and iodine (2.38 Å) as seen in Table 2.60
| Co-crystal | X⋯N | C–X⋯N | van der Waals reduction |
|---|---|---|---|
| F 5 BAI-PyrFur 2 | 2.74 | 175.1 | 34.3 |
| F 5 BAI-PyrThio 2 | 2.70 | 179.3 | 35.3 |
Three other pair-wise contacts are listed on the right side of Fig. 2, all of which are π-stacking interactions. One of the π-stacking interactions is heterogeneous, meaning it contains one XB donor molecule and one XB acceptor molecule. This contact has an intermolecular distance of 4.18 Å, which corresponds to the geometric center of the 6-membered benzene ring in the F5BAI XB donor and the equivalent pyridine center in the PyrFur2 XB acceptor. The other two π-stacking interactions are homogeneous, containing either two XB donor molecules or two XB acceptor molecules. The XB donor homogeneous π-stacking interaction has an intermolecular distance of 5.01 Å, while the XB acceptor homogeneous π-stacking interaction has an intermolecular distance of 3.53 Å (both of which are distances between the geometric centers of the 6-membered rings). Seventeen other unique contacts were also identified in the F5BAI-PyrFur2 co-crystal and are depicted in Fig. S5 of the ESI.†
Comparatively, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
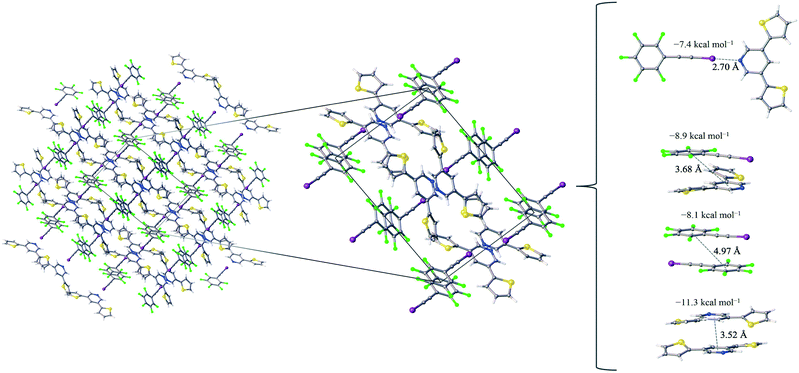
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 assembly of the F5BAI-PyrThio2 co-crystal exhibits a monoclinic structure with the P21/c space group (Fig. 3). XB donors and acceptors align in an alternating fashion along the c-axis to form XB dimers, which in turn pack antiparallel to each other along the a-axis. The F5BAI-PyrThio2 co-crystal exhibits crystallographic disorder with two fundamentally different configurations of the PyrThio2 XB acceptor. The crystallographic disorder reveals itself as a 60% partial occupancy for a configuration with the sulfur atoms of the thiophene rings oriented in opposite directions, one pointing towards and the other away from the nitrogen atom of the central pyridine ring (e.g., τα ≈ 170° and τβ ≈ 25°, as depicted in Fig. 1c). The other configuration has 40% partial occupancy in which both sulfur atoms are pointing towards the nitrogen atom on pyridine (τα and τβ ≈ 165°). The 60% occupancy configuration (sulfur atoms oriented in opposite directions) is discussed in the text, whereas all configurations are fully reported in the ESI.† As with PyrFur2, full geometry optimizations of PyrThio2 identify several energetically competitive configurations. However, the energy differences are even smaller. The two lowest energy configurations are separated by only +0.05 kcal mol−1 at the M06-2X/aug-cc-pVTZ-PP level of theory (one configuration with τα and τβ ≈ 27° and the other with τα ≈ 154° and τβ ≈ 27°). In light of the small conformational energy differences computed for both pyridine fragments, the orientations observed in the crystal structures suggest that local environmental effects in the solid state likely influence the configurations adopted by the XB acceptors. A more detailed conformational analysis is underway to better understand these subtle structural differences between the two systems. Similarly to the F5BAI-PyrFur2 co-crystal, a XB interaction is observed in the F5BAI-PyrThio2 co-crystal where the N⋯I–C angle is 179° and the N⋯I distance is 2.70 Å corresponding to a 35.3% bond shortening relative to the total van der Waals radii of nitrogen and iodine (Table 2).60 The three types of π-stacking (heterogeneous, homogeneous with two XB donors and homogeneous with two XB acceptors) are also seen in the F5BAI-PyrThio2 co-crystal (right side of Fig. 3), and have the same type of intermolecular distances as seen in the F5BAI-PyrFur2 co-crystal (distances between geometric centers of 6-membered rings).
1 assembly of the F5BAI-PyrThio2 co-crystal exhibits a monoclinic structure with the P21/c space group (Fig. 3). XB donors and acceptors align in an alternating fashion along the c-axis to form XB dimers, which in turn pack antiparallel to each other along the a-axis. The F5BAI-PyrThio2 co-crystal exhibits crystallographic disorder with two fundamentally different configurations of the PyrThio2 XB acceptor. The crystallographic disorder reveals itself as a 60% partial occupancy for a configuration with the sulfur atoms of the thiophene rings oriented in opposite directions, one pointing towards and the other away from the nitrogen atom of the central pyridine ring (e.g., τα ≈ 170° and τβ ≈ 25°, as depicted in Fig. 1c). The other configuration has 40% partial occupancy in which both sulfur atoms are pointing towards the nitrogen atom on pyridine (τα and τβ ≈ 165°). The 60% occupancy configuration (sulfur atoms oriented in opposite directions) is discussed in the text, whereas all configurations are fully reported in the ESI.† As with PyrFur2, full geometry optimizations of PyrThio2 identify several energetically competitive configurations. However, the energy differences are even smaller. The two lowest energy configurations are separated by only +0.05 kcal mol−1 at the M06-2X/aug-cc-pVTZ-PP level of theory (one configuration with τα and τβ ≈ 27° and the other with τα ≈ 154° and τβ ≈ 27°). In light of the small conformational energy differences computed for both pyridine fragments, the orientations observed in the crystal structures suggest that local environmental effects in the solid state likely influence the configurations adopted by the XB acceptors. A more detailed conformational analysis is underway to better understand these subtle structural differences between the two systems. Similarly to the F5BAI-PyrFur2 co-crystal, a XB interaction is observed in the F5BAI-PyrThio2 co-crystal where the N⋯I–C angle is 179° and the N⋯I distance is 2.70 Å corresponding to a 35.3% bond shortening relative to the total van der Waals radii of nitrogen and iodine (Table 2).60 The three types of π-stacking (heterogeneous, homogeneous with two XB donors and homogeneous with two XB acceptors) are also seen in the F5BAI-PyrThio2 co-crystal (right side of Fig. 3), and have the same type of intermolecular distances as seen in the F5BAI-PyrFur2 co-crystal (distances between geometric centers of 6-membered rings).
The heterogeneous π-stacking has an intermolecular distance of 3.68 Å, which is 0.5 Å less than that of F5BAI-PyrFur2. The two homogeneous π-stacking have intermolecular distances that are very similar to those seen in the F5BAI-PyrFur2 co-crystal, with deviations of −0.04 Å for the two XB donor molecules and −0.01 Å for the two XB acceptor molecules. Sixteen other unique contacts were also identified in the F5BAI-PyrThio2 co-crystal and are depicted in Fig. S6 of the ESI.†
3.3 Theoretical results
The computational procedures employed here have been calibrated and shown to reproduce geometries and dissociation energies for a large set of XB dimers.49 These DFT computations were performed to quantify the relative strength of all nearest neighbor pair-wise interactions forming the molecular assembly. A total of twenty-one unique nearest neighbor contacts were identified and characterized in the F5BAI-PyrFur2 co-crystal, along with twenty for the F5BAI-PyrThio2 co-crystal. The M06-2X interaction energies with and without the Boys–Bernardi counterpoise procedure as well as the average of both values for the dominant pair-wise contacts observed in the co-crystals are summarized in Table 3.| Interaction | F 5 BAI-PyrFur 2 | F 5 BAI-PyrThio 2 | ||||
|---|---|---|---|---|---|---|
| E int | E CPint | E avgint | E int | E CPint | E avgint | |
| XB | −7.6 | −7.5 | −7.6 | −7.5 | −7.4 | −7.4 |
| Donor–acceptor π-stack | −7.3 | −6.3 | −6.8 | −9.5 | −8.3 | −8.9 |
| Donor–donor π-stack | −7.7 | −6.6 | −7.2 | −8.7 | −7.5 | −8.1 |
| Acceptor acceptor π-stack | −8.7 | −7.9 | −8.3 | −11.7 | −10.9 | −11.3 |
The F5BAI-PyrFur2 co-crystal has a XB interaction of −7.6 kcal mol−1 (Eavgint) and three different types of π-stacking interactions (heterogeneous, homogeneous with two XB donors and homogeneous with two XB acceptors as previously defined and shown in Fig. 2) ranging from −6.8 kcal mol−1 to −8.3 kcal mol−1. The heterogeneous π-stacking has the smallest average interaction energy of −6.8 kcal mol−1, whereas the homogeneous π-stacking types are −7.2 kcal mol−1 and −8.3 kcal mol−1 for the two XB donors and two XB acceptors, respectively. All of the other interactions within this co-crystal were less than 2.1 kcal mol−1 and correspond to various heterogeneous and homogeneous edge–edge and slipped π-stacking arrangements. Interaction energies, structures and Cartesian coordinates for all twenty-one pair-wise contacts of the F5BAI-PyrFur2 co-crystal are reported in Fig. S5, Tables S2, and S24–S44† within the ESI.†
The F5BAI-PyrThio2 co-crystal has a XB interaction of −7.4 kcal mol−1, which is nearly isoenergetic with that of the F5BAI-PyrFur2 co-crystal (within 0.2 kcal mol−1). This co-crystal also exhibits the same three types of π-stacking (heterogeneous, homogeneous with two XB donors and homogeneous with two XB acceptors) ranging from −8.1 kcal mol−1 to −11.3 kcal mol−1. Similar to the F5BAI-PyrFur2 co-crystal, the π-stacking interactions identified in the F5BAI-PyrThio2 co-crystal are larger than the corresponding XB interaction, however in this case, the energetic difference exceeds 3.5 kcal mol−1. Moreover, the homogeneous π-stacking interaction between two XB acceptors is significantly larger than that of the F5BAI-PyrFur2 co-crystal (−8.3 kcal mol−1vs. −11.3 kcal mol−1). This is most likely due to the fact that sulfur is far more polarizable than oxygen. All of the other interactions within this co-crystal were less than 2.1 kcal mol−1 and correspond to various heterogeneous and homogeneous edge–edge, slipped π-stacking and herringbone arrangements. Interaction energies, structures and Cartesian coordinates for all twenty pair-wise contacts of the F5BAI-PyrThio2 co-crystal are reported in Fig. S6–S9, Tables S3–S6 and S45–S124 within the ESI,† for all the configurations of PyrThio2.
Additionally, the effects of the assigned hydrogen atom positions in the crystal structures on the computed interaction energies have been examined by a series of constrained geometry optimizations. For all 41 fragment pairs discussed in this section, the positions of the hydrogen atoms were optimized at the M06-2X/aug-cc-pVDZ-PP level of theory while fixing the coordinates of all other atoms. This procedure introduced only small changes to the interaction energies (all of which can be found in the ESI†). For the pair-wise interactions in the F5BAI-PyrFur2 co-crystal, the absolute change to Eavgint was less than 0.1 kcal mol−1 on average. The maximum absolute deviation for the 21 F5BAI-PyrFur2 pairs is 0.41 kcal mol−1 (corresponding to a relative absolute difference of 4% in a strongly interacting pair), and the maximum relative absolute deviation is 19% (corresponding to an absolute different of 0.04 kcal mol−1 in a weakly interacting pair). The effect of optimizing the hydrogen atom positions is even smaller in the 20 F5BAI-PyrThio2 pairs that have been examined. The maximum absolute change to Eavgint was only 0.23 kcal mol−1 which also corresponds to the largest relative absolute difference (15%) observed in these systems. These results suggest that refining the hydrogen atom positions would have only a minor effect on the M06-2X/aug-cc-pVTZ-PP interaction energies reported in Table 3 and the ESI.†
4 Conclusions
In summary, the present study describes the preparation and characterization of two co-crystals resulting from the self-assembly of an excellent XB donor F5BAI with one of two closely related optoelectronic building blocks that can act as an XB acceptor (PyrFur2 or PyrThio2). Spectroscopic and thermal analyses indirectly indicate the presence of XB interactions in both the F5BAI-PyrFur2 and F5BAI-PyrThio2 co-crystals. X-ray crystallography provides direct evidence of the XB and π-type contacts, while theoretical characterization revels that the XB and π-stacking have the largest interaction energies.Even though both XB acceptors contain the same basic structure resulting in very similar interactions, the conformations adopted by the furan and thiophene substituents are quite different in the co-crystals. The PyrFur2 XB acceptor only adopts a single, nearly planar configuration (τα and τβ ≈ 3°) with the oxygen atoms of both furan substituents pointing away from the nitrogen atom of the central pyridine ring as depicted in Fig. 1b. In contrast, the F5BAI-PyrThio2 co-crystal exhibits crystallographic disorder with two different configurations of the XB acceptor. In the somewhat more prevalent configuration of the PyrThio2 fragment (60% occupancy) the sulfur atoms of the thiophene rings are essentially oriented in opposite directions with one pointing towards and the other away from the nitrogen atom of the pyridine (e.g., τα ≈ 170° and τβ ≈ 25°). In the less common configuration (40% occupancy), both sulfur atoms are directed towards the nitrogen atom of pyridine (τα and τβ ≈ 165°). Additionally, the PyrThio2 XB acceptor is far less planar in its co-crystal than PyrFur2 as indicated by the chalcogen torsional angles (τα and τβ). A detailed conformational analysis is currently underway in order to better understand these conformational preferences.
Both systems have nearly identical interaction energies associated with the XB pair-wise contacts (Eavgint = −7.5 ± 0.1 kcal mol−1). In both systems, the only other sizeable interactions are the hetero- and homogeneous π-type stacking interactions between the XB donor and XB acceptor units. In F5BAI-PyrFur2 co-crystal, these pair-wise stacking interactions are quite similar in magnitude to the XB contact (Eavgint ranging from −6.8 to −8.3 kcal mol−1), whereas they are noticeably larger in the F5BAI-PyrThio2 co-crystal (Eavgint ranging from −8.1 to −11.3 kcal mol−1), likely due to the enhanced polarizability of the sulfur atoms in thiophene compared to the oxygen atoms in furan. All of the other pair-wise interaction energies analyzed had appreciably smaller magnitudes (Eavgint typically less than −1.0 kcal mol−1 and never exceeding −2.1 kcal mol−1).
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The experimental work is supported by NSF under Grant number(s) CHE-1652094 and CHE-1460568 (J. L. N., N. S., D. T. N., and D. L. W.) The computational work is supported by the Mississippi Center for Supercomputing Research and NSF under Grant number(s) CHE-1338056 and CHE-1664998 (S. N. J., T. L. E. and G. S. T.).Notes and references
- M. A. Uddin, T. H. Lee, S. Xu, S. Y. Park, T. Kim, S. Song, T. L. Nguyen, S.-J. Ko, S. Hwang, J. Y. Kim and H. Y. Woo, Chem. Mater., 2015, 27, 5997–6007 CrossRef CAS.
- C. Zhu, A. U. Mu, Y.-H. Lin, Z.-H. Guo, T. Yuan, S. E. Wheeler and L. Fang, Org. Lett., 2016, 18, 6332–6335 CrossRef CAS PubMed.
- R. V. Kazantsev, A. J. Dannenhoffer, T. Aytun, B. Harutyunyan, D. J. Fairfield, M. J. Bedzyk and S. I. Stupp, Chem, 2018, 4, 1596–1608 CAS.
- N. T. Shewmon, D. L. Watkins, J. F. Galindo, R. B. Zerdan, J. Chen, J. Keum, A. E. Roitberg, J. Xue and R. K. Castellano, Adv. Funct. Mater., 2015, 25, 5166–5177 CrossRef CAS.
- P. Gomez, S. Georgakopoulos, J. P. Ceron, I. da Silva, M. Mas-Montoya, J. Perez, A. Tarraga and D. Curiel, J. Mater. Chem. C, 2018, 6, 3968–3975 RSC.
- H. Liu, L. Huang, X. Cheng, A. Hu, H. Xu, L. Chen and Y. Chen, ACS Appl. Mater. Interfaces, 2017, 9, 1145–1153 CrossRef CAS PubMed.
- R. Fang, R. Chen, J. Gao, H. Zhang, H. Wu and H. Li, Org. Electron., 2017, 45, 108–114 CrossRef CAS.
- B. Feringán, P. Romero, J. L. Serrano, C. L. Folcia, J. Etxebarria, J. Ortega, R. Termine, A. Golemme, R. Giménez and T. Sierra, J. Am. Chem. Soc., 2016, 138, 12511–12518 CrossRef PubMed.
- H. G. Kim, B. Kang, H. Ko, J. Lee, J. Shin and K. Cho, Chem. Mater., 2015, 27, 829–838 CrossRef CAS.
- X. Guo, Q. Liao, E. F. Manley, Z. Wu, Y. Wang, W. Wang, T. Yang, Y.-E. Shin, X. Cheng, Y. Liang, L. X. Chen, K.-J. Baeg, T. J. Marks and X. Guo, Chem. Mater., 2016, 28, 2449–2460 CrossRef CAS.
- Y. Wang, T. Hasegawa, H. Matsumoto, T. Mori and T. Michinobu, Adv. Funct. Mater., 2016, 27, 1604608 CrossRef.
- N. Leclerc, P. Chávez, O. A. Ibraikulov, T. Heiser and P. Lévêque, Polymer, 2016, 8, 11–38 Search PubMed.
- H. Guo, T. Shen, F. Wu, G. Wang, L. Ye, Z. Liu, B. Zhao and S. Tan, RSC Adv., 2016, 6, 13177–13184 RSC.
- W. Chao, L. Zhaoxia, G. Huan and T. Songting, Macromol. Chem. Phys., 2017, 218, 1700094 CrossRef.
- V. Sureshraju, C. Bo-Chin, P. Pragya, H. Deng-Yi, W. Kuan-Yi, L. Long-Huan, C. Wei-Chieh, L. Yi-Yo, H. Shao-Huan, Y. Bo-Chun, W. Chien-Lung, C. Wen-Jung, L. Cheng-Liang, C. Ming-Chou and F. Antonio, Adv. Mater., 2017, 29, 1702414 CrossRef PubMed.
- D. Tao, L. Lei, F. Linlin, X. Yu, D. Wei, Y. Pan, Y. Bei, D. Shang, F. Antonio, D. Huanli and H. Hui, Adv. Mater., 2017, 29, 1606025 CrossRef PubMed.
- Y. Lei, G. Wenxing, Y. Yufei, H. Ling, Z. Xutao, X. Yu, W. Xiaoxi, P. Aidong and H. Hui, Small Methods, 2018, 2, 1700330 CrossRef.
- D. Tao, W. Kaikai, C. Jun, X. Jin, F. Weili, M. Han, Y. Lei, W. Xiaoxi, X. Fujian, P. Aidong and H. Hui, Adv. Funct. Mater., 2018, 28, 1800135 CrossRef.
- S. Yu, Y. Chen, L. Yang, P. Ye, J. Wu, J. Yu, S. Zhang, Y. Gao and H. Huang, J. Mater. Chem. A, 2017, 5, 21674–21678 RSC.
- P. Ye, Y. Chen, J. Wu, X. Wu, S. Yu, W. Xing, Q. Liu, X. Jia, A. Peng and H. Huang, J. Mater. Chem. C, 2017, 5, 12591–12596 RSC.
- Y. Liu, C. Zhang, D. Hao, Z. Zhang, L. Wu, M. Li, S. Feng, X. Xu, F. Liu, X. Chen and Z. Bo, Chem. Mater., 2018, 30, 4307–4312 CrossRef CAS.
- S. T. Nguyen, T. L. Ellington, K. E. Allen, J. D. Gorden, A. L. Rheingold, G. S. Tschumper, N. I. Hammer and D. L. Watkins, Cryst. Growth Des., 2018, 18, 3244–3254 CrossRef CAS.
- S. T. Nguyen, A. L. Rheingold, G. S. Tschumper and D. L. Watkins, Cryst. Growth Des., 2016, 16, 6648–6653 CrossRef CAS.
- J. Wilson, J. S. Dal Williams, C. Petkovsek, P. Reves, J. W. Jurss, N. I. Hammer, G. S. Tschumper and D. L. Watkins, RSC Adv., 2015, 5, 82544–82548 RSC.
- G. R. Desiraju, P. H. Shing, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711–1713 CAS.
- G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601 CrossRef CAS PubMed.
- P. Metrangolo and G. Resnati, IUCrJ, 2014, 1, 5–7 CrossRef CAS PubMed.
- P. Politzer and J. S. Murray, Crystals, 2017, 7, 212–226 CrossRef.
- P. Politzer, J. S. Murray, T. Clark and G. Resnati, Phys. Chem. Chem. Phys., 2017, 19, 32166–32178 RSC.
- T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296 CrossRef CAS PubMed.
- P. Metrangolo, F. Meyer, T. Pilati, G. Resnati and G. Terraneo, Angew. Chem., Int. Ed., 2008, 47, 6114–6127 CrossRef CAS PubMed.
- P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2010, 12, 7748–7757 RSC.
- C. Wang, D. Danovich, Y. Mo and S. Shaik, J. Chem. Theory Comput., 2014, 10, 3726–3737 CrossRef CAS PubMed.
- M. H. Kolář and P. Hobza, Chem. Rev., 2016, 116, 5155–5187 CrossRef PubMed.
- M. Jeffies-EL, B. M. Kobilka and B. J. Hale, Macromolecules, 2014, 47, 7253–7271 CrossRef.
- Z. Zhao, H. Nie, C. Ge, Y. Cai, Y. Xiong, J. Qi, W. Wu, R. T. K. Kwok, X. Gao, A. Qin, J. W. Y. Lam and B. Z. Tang, Adv. Sci., 2017, 4, 1700005 CrossRef PubMed.
- D. Chandran, T. Marszalek, W. Zajaczkowski, P. K. Madathil, R. K. Vijayaraghavan, Y.-H. Koh, S.-Y. Park, J. R. Ochsmann, W. Pisula and K.-S. Lee, Polymer, 2015, 73, 205–213 CrossRef CAS.
- A. A. Virkar, S. Mannsfeld, Z. Bao and N. Stingelin, Adv. Mater., 2010, 22, 3857–3875 CrossRef CAS PubMed.
- D. Franchini, F. Dapiaggi, S. Pieraccini, A. Forni and M. Sironi, Chem. Phys. Lett., 2018, 712, 89–94 CrossRef CAS.
- C. B. Aakeröy, T. K. Wijethunga, J. Desper and M. Daković, Cryst. Growth Des., 2015, 15, 3853–3861 CrossRef.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Am. Chem. Soc., 1995, 117, 1090–1097 CrossRef CAS.
- K. A. Peterson and B. C. Shepler, J. Phys. Chem. A, 2006, 110, 13877–13883 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- S. Kozuch and J. M. L. Martin, J. Chem. Theory Comput., 2013, 9, 1918–1931 CrossRef CAS PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- H. B. Jansen and P. Ros, Chem. Phys. Lett., 1969, 3, 140–143 CrossRef CAS.
- N. R. Kestner, J. Chem. Phys., 1968, 48, 252–257 CrossRef CAS.
- B. Liu and A. D. McLean, J. Chem. Phys., 1973, 59, 4557–4558 CrossRef CAS.
- G. S. Tschumper, Rev. Comput. Chem., 2009, 26, 39–90 CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian09 Revision E.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- N. Schultheiss and A. Newman, Cryst. Growth Des., 2009, 9, 2950–2967 CrossRef CAS PubMed.
- S. Cherukuvada and T. N. Guru Row, Cryst. Growth Des., 2014, 14, 4187–4198 CrossRef CAS.
- H. Tsuji and E. Nakamura, Acc. Chem. Res., 2017, 50, 396–406 CrossRef CAS PubMed.
- O. Gidron, Y. Diskin-Posner and M. Bendikov, J. Am. Chem. Soc., 2010, 132, 2148–2150 CrossRef CAS PubMed.
- M. Rahm and R. Hoffmenn, Chem. – Eur. J., 2016, 22, 14625–14632 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Including additional synthetic details, summary of theoretical calculations, structural figures, TG/DTZ plots, and X-ray crystallographic tables containing bond distances and angles. CCDC 1876245 and 1876246. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9ce00219g |
| This journal is © The Royal Society of Chemistry 2019 |