Systematically improved melting point prediction: a detailed physical simulation model is required

Abstract

Accurate prediction of fundamental properties such as melting points using direct physical simulation is challenging. Here, we investigate the melting point (T_m) of alkali halides that are often considered to be the simplest category of salts. Popular force fields that have been examined for this task leave considerable room for improvement. Recently we introduced a new force field for alkali halides (WBK) as part of the Alexandria project, featuring explicit polarisation and distributed charges. This new force field significantly improves the prediction of a large set of physicochemical properties and in this contribution we show that the same is valid for the prediction of T_m. For reference, we calculated T_m using a non-polarisable force field by Joung and Cheatham (JC), and compare our results to existing literature data on the widely used Tosi–Fumi (TF) parameters. In contrast to the predictions of the WBK model, the JC force field consistently overestimates the experimental T_m, while the accuracy of the TF model strongly depends on the investigated salt. Our results show that the inclusion of more realistic physics into a force field opens up the possibility to accurately describe many physicochemical properties over a large range of temperatures, even including phase transitions.

---

Phase transitions are an everyday phenomenon that have considerable impact on our lives. Despite their ubiquity and technological importance, the atomistic details, microscopic kinetics and thermodynamics are not yet completely understood.^1–4 This can partially be attributed to the challenge to study such transitions experimentally on an atomistic level, in particular the initial stages and underlying dynamics.^2,5 The development of accurate models for computer simulations can contribute to this critical issue and we have recently published a new set of polarisable interionic potentials for alkali halides.⁶ Their widespread existence and relevance in nature and technological applications make alkali halides an important target for study.^7–15 The force field was developed to accurately describe gas phase properties, such as vibrational frequencies and dipole moments, as well as crystal densities at room temperature, with the ultimate goal to be phase transferable.⁶ In our recent contributions, we showed that this is the case. The force field performs well for molten salts, both pure alkali halides and mixtures, with improved results for equilibrium and dynamical properties in comparison to both experiments and other force fields.^6,16,17

In contrast to molecular mechanics, ab initio quantum chemistry calculations are in general considered to provide the most accurate approach to calculate physicochemical properties via computer simulations. Melting points have been determined using ab initio Molecular Dynamics (MD), however this is computationally demanding, in particular for strongly ionic substances,¹⁸ and the accuracy is limited by sampling and system size convergence.¹⁹ Wang et al. determined e.g. the melting point of tungsten with an error of 7% of the experimental value. A more recent study by Rang & Kresse determined e.g. the melting point of MgO using a first principles approach with an accuracy of ≈2–11%, depending on the applied functionals.¹⁸ To our knowledge no ab initio melting simulations for alkali halides have been reported. Besides melting points, other properties were evaluated for alkali halides using first principle calculations. Gopikrishnan et al.²⁰ calculated lattice energies of alkali halides with an RMSD of ≈70 kJ mol⁻¹ that, in fact, can be predicted more accurately by our polarizable model using classical MD simulations (RMSD 16 kJ mol⁻¹) and other force fields.⁶ On the other hand, first principle calculations offer the possibility to calculate properties such as the band-structures of materials that cannot be obtained with classical simulations.²⁰ However, quantum chemistry methods remain severely limited by computational demands and nanosecond simulations for systems of thousands of particles are still firmly out of reach for first principles MD simulations. Therefore, accurate classical MD simulations remain the most practical route to study properties such as melting points of complex systems.

In a previous evaluation, Aragones et al. pointed out that “there is still room for improvement in the area of force-fields for alkaline halides, given that so far most models are still unable to describe a simple yet important property such as the melting point”.²¹ In the energy industry molten salts play an important role for use as solvent, e.g. in the production of aluminium⁹ or in pyroprocessing of nuclear waste,¹⁰ as heat transfer medium,¹¹ as thermal energy storage in concentrated power plants,^12,13 or as electrolyte in liquid metal batteries.^14,15 In these applications, the melting point, T_m, is of particular interest as it defines the minimal temperature at which the salts can be used in the liquid state. Often eutectic salt mixtures are used in industry, providing the advantage of a significantly lowered melting point, and a direct liquid–solid phase transition thereby avoiding mixed phases, that is where solid and liquid phase are present at the same time. In our latest contribution we showed that our polarisable force field is indeed able to accurately predict physicochemical properties, such as the conductivity, of such a mixture.¹⁷

As an alternative to using polarisable models, Leontyev and Stuchebrukhov^22–25 introduced ions with effective charges that are scaled down in order to mimic the electronic dielectric screening in condensed matter. Such models work in conjunction with other effective-charge empirical models such as popular water models. Fuentes-Azcatl & Barbosa explored this charge scaling approach for some alkali halide ions (Na⁺, K⁺, Cl⁻ and Br⁻) and observed that in pure alkali halide salts the lattice energies are significantly off (>10%) despite correct crystal densities.^26,27

The theory behind the melting of alkali halides, of both single component and binary mixtures, was reviewed by Galwey.^3,28,29 In general, the structural changes that occur when crystals melt are not known in detail, and the physical mechanism is not properly understood.^1–5 Indeed, little is known about the spatial interrelationships of the components within the melt formed at temperatures at and immediately above T_m.³ It is pointed out that the knowledge of the molten state is incomplete, including the relationships between thermodynamic properties and structures.³⁰ Using our new force field we were able contribute to this issue, by directly connecting structural, dynamical and thermodynamical properties in molten salts.^16,17

Two main definitions have been used to investigate melting:⁴ (i) the melting point is considered to be the point where the Gibbs free energy of the solid equals that of the melt; (ii) there are characteristic changes in the solid as T_m is approached, e.g. the formation of a critical concentration of Schottky defects.^31–33 However, there is still no generally acceptable theoretical model for melting or identification of the factors that control the transformation of solid crystal to liquid melt.^1,3

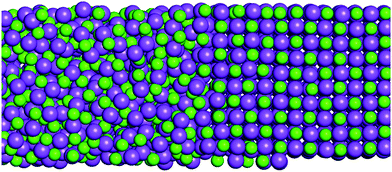
For determining the melting points computationally we choose the so-called liquid–solid direct coexistence method (Fig. 1).^34–36 Other applicable methods would be e.g. free energy calculations or the Hamiltonian Gibbs–Duhem integration.^21,37 These different methods were tested by Aragones et al. on alkali halides, and shown to give consistent results. Regarding the liquid–solid coexistence method, a starting configuration has to be set up where the solid crystal is in direct contact with its melt (Fig. 1). The liquid–solid coexistence box is then simulated using constant pressure simulations at different temperatures. Depending on the temperature, the system evolves either to become a crystal or a melt. The different salts are simulated in a wide range of temperatures around the experimental melting point to determine the melting point of the force field, T_m,ff. It is determined here by the average of the highest temperature where the salt is still a solid and the lowest temperature where the salt is a melt. In order to evaluate the final phase (i.e. solid or liquid) of the simulated salt boxes that were run for 5 ns at each temperature, both diffusion coefficients and radial distribution functions were evaluated for the last 100 ps. Using the diffusion coefficients it was determined whether the salt was liquid or solid, while the radial distribution function allowed us in addition to investigate the solid's crystallinity (i.e. whether the crystal structure was stable). For more details the reader is referred to the ESI.† Recently, Martiniani et al. proposed an information-theoretic approach to detect phase transitions from the size of a compressed trajectory file.³⁸ The rationale for this is that a solid is more ordered than a liquid and therefore compression algorithms should be able to decrease file size more. We tested this approach on the final structure files of our WBK coexistence simulations and confirmed that the method yielded the same results as the diffusion test described above (see ESI,† Fig. S1).

Fig. 1 Section of a NaCl liquid–solid coexistence simulation box at the interface.

For the evaluation of the melting points of alkali halides with a fcc structure at high temperature (i.e. all alkali halides except CsBr and CsI), we employed our polarisable force field (called WBK, Wang-Buckingham)⁶ and a non-polarisable force field due to Joung & Cheatham,³⁹ dubbed JC (the variant that is compatible with TIP3P water⁴⁰ was used). Our results are compared to literature results from Aragones et al.²¹ who tested three force fields for NaCl (JC (SPC/E-compatible), Smith–Dang (SD),^41,42 and Tosi–Fumi (TF⁴³)). In that work, the salt-specific TF parameters were applied for eleven alkali halides (LiF, LiCl, NaF, NaCl, NaBr, KF, KCl, KBr, RbF, RbCl and RbBr). Joung & Cheatham presented three sets of ion-specific parameters for the AHs, which are compatible with the water models TIP3P,⁴⁰ TIP4P_EW⁴⁴ and SPC/E.⁴⁵ While Aragones et al. tested the SPC/E-compatible set for NaCl, we choose to test the TIP3P-compatible set. There are several differences that distinguish the applied force fields: (i) the WBK, JC and SD force field use ion-specific parameters, whereas the TF model uses salt-specific parameters; (ii) the WBK model is polarisable using a core–shell model, while the JC, SD and TF model are non-polarisable; (iii) the WBK model uses distributed charges, while the JC, SD and TF model use point charges; (iv) the van der Waals interactions are modelled differently: WBK uses a buffered Buckingham potential that has no singularity and has in general a softer repulsive part,⁴⁶ JC and SD use a 12-6 Lennard-Jones (LJ) potential, and the TF model employs a Buckingham potential that is extended by a r⁻⁸ term. (v) JC and SD use the Loretz–Berthelot combining rules, TF has no combining rules as the parameters are salt-specific, and WBK uses combing rules introduced by Hogervorst.⁴⁷

Fig. 2 shows the calculated melting points for all alkali halides (AHs) that reside in a NaCl-structure at high temperature in comparison to experimental data (black). In addition to our results using the polarisable force field (WBK, light blue) and the non-polarisable force field (JC (TIP3P-compatible), green rhomb), also results from Aragones et al. are shown for comparison.²¹ Most of the results from Aragones, i.e. melting points for 11 AHs, were calculated applying the Born–Mayer–Huggins potential using the Tosi–Fumi (TF) salt-specific parameters that have been used extensively for simulating AHs (red).^48–54 Additionally, Aragones et al. calculated the melting point of NaCl with two other force fields, namely JC (SPC/E-compatible),³⁹ and the model by Smith & Dang (SD).^41,42

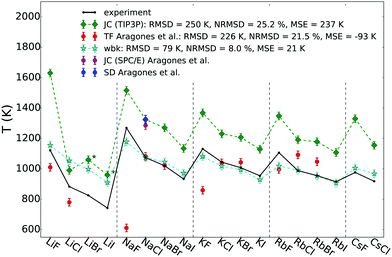Fig. 2 Melting point temperatures for all AHs with NaCl structure at high temperature using the polarisable WBK (light blue) and the non-polarisable JC (TIP3P variant, green rhomb) force field. For reference also melting points calculated by Aragones et al. using other non-polarisable force fields are added using the Tosi–Fumi potential (red), and for NaCl also JC(SPC/E) and SD, as well as experimental data (black).⁵⁵ In the legend the RMSD (root mean square deviation), the NRMSD (normalised RMSD) and the MSE (mean signed error) are given. Numerical values are listed in Table S2 (ESI†). The * indicates that the NaCl-cyrstal structure of LiBr and LiI using the JC (TIP3P) force field was not stable in the liquid–solid coexistence simulation at the temperatures tested.

From Fig. 2 it is clear that the non-polarisable force field from JC (TIP3P-compatible) systematically overestimates the melting points with a root mean square deviation (RMSD) of 250 K and a mean signed error (MSE) of 237 K. In contrast, the accuracy of the melting points determined using the non-polarisable TF model vary. There is good agreement with the experimental melting points for certain salts, such as NaCl, NaBr, KCl and KBr, but less good agreement for the other tested salts, with the largest deviation for NaF (≈600 K). The results show that in principle it is possible to obtain accurate melting points using a non-polarisable force field; the key being the parameterisation of the force field and the properties that the model is optimised for. While it might be simple to predict one specific property, it is very challenging to model many different properties accurately at the same time, even more so over a large range of temperatures that might include phase transitions.⁵⁶ Already in the 70s it was noticed by Adams & McDonald,⁴⁸ Lewis et al.,⁴⁹ Michielsen et al.⁵⁷ and Ciccotti et al.⁵⁰ that the TF potential has severe deficiencies to describe certain physicochemical properties of some salts. In particular the inclusion of polarisability might be crucial for a better description of high temperature physicochemical properties.^48,58 The TF model does not seem to be reliable enough to predict many different physicochemical properties which suggests that even more care is needed when applying such a force field to mixtures of salts. Nevertheless, there are recent examples of the use of TF salt-specific parameters for mixtures.^51,52 The T_m for the 11 salts investigated²¹ has an RMSD of 226 K with a MSE or −93 K, caused by the fact that the TF parameters significantly underestimate some of the melting points. Lewis et al.⁴⁹ investigated LiI (which is not included in the study by Aragones et al.) using the TF parameters, and observed that the crystal (simulated with 3-dimensional boundary conditions) is not stable at the melting point, but melts: this indicates that the force field's melting point is at least 20–30% too low for this salt.⁵⁹ The other tested force fields, JC (SPC/E-compatible) and SD, overestimate the experimental value of NaCl by more than 200 K, and are very close to the predicted value by JC (TIP3P-compatible).

The polarisable WBK force field (stars, light blue) performs significantly better than the other non-polarisable force fields, and the systematically improved predicted melting points follow the experimental trend rather well, with the largest deviation for LiCl, LiBr and LiI. For the polarisable force field WBK we find an RMSD of 79 K and a MSE of 21 K. The RMSD is three times lower than for JC and the accuracy of prediction of the melting points of alkali halides using computer simulations is to the best of our knowledge unprecedented.

The Li-salts seem to be more challenging to model accurately and this could be related to the stability of the crystal structure in the liquid–solid coexistence box. While no stability issues were observed with the solid fraction using the WBK force field, we indeed observed that the crystal structure of LiBr and LiI changed using the JC (TIP3P-compatible) force field. In fact, it was not possible to obtain a stable starting configuration where on the one side the solid would remain in the NaCl-structure with the other side being a melt for these two salts using the JC force field. Instead the crystal structure changed (see ESI,† radial distribution functions). The melting point was still determined, but it does not correspond to the true melting point from a NaCl-crystal structure and is therefore marked with a star in Fig. 2. Also using the TF potential it was observed that the LiI crystal is not stable.⁴⁹ Those results show indeed that the polarisable WBK model presents a significant improvement for such challenging salts that seem to be demanding to model computationally. In fairness, even for WBK the largest deviations from the experimental T_m are observed for LiCl, LiBr and LiI (see ESI,† Table S2) suggesting that these salts are more difficult to model in general, perhaps due to the larger difference in size between cation and anion.

In this contribution we have demonstrated that the inclusion of explicit polarisation and distributed charges as well as more physical van der Waals interaction in models of alkali halides dramatically increases the predictive power, to the point where even very challenging properties such as T_m can be derived with reasonable accuracy. It is important to point out that the WBK model resulted from systematic testing and development of a range of different potentials.⁶ Therefore, it is now possible to model many physicochemical properties, over a large range of temperatures, even including phase transitions. A polarisable model comes at extra computational costs, however, especially when investigating properties that rely on an accurate description of dynamic properties the inclusion of polarisability is the road ahead.^16,17 The mechanisms behind melting and phase-transitions at large are still not completely understood but we are confident that with improved accurate force fields in general it will be possible to gain further insights in these processes. Such theoretical methods can contribute to the prediction of phase-transition processes that are challenging to capture experimentally.

The Swedish research council is acknowledged for grants of computer time (SNIC2017-12-41, SNIC2018-2-42) through the High Performance Computing Center North in Umeå, Sweden. Funding from eSSENCE – The e-Science Collaboration (Uppsala-Lund-Umeå, Sweden) is gratefully acknowledged.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. F. Wang, Z. Wang, Y. Peng, Z. Zheng and Y. Han, Soft Matter, 2018, 14, 2447–2453.
2. K.-i. Murata, H. Asakawa, K. Nagashima, Y. Furukawa and G. Sazaki, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E6741–E6748.
3. A. Galwey, J. Therm. Anal. Calorim., 2005, 82, 23–40.
4. J. Shanker and M. Kumar, Phys. Status Solidi B, 1990, 158, 11–49.
5. Z. Wang, F. Wang, Y. Peng and Y. Han, Nat. Commun., 2015, 6, 6942.
6. M. M. Walz, M. M. Ghahremanpour, P. J. van Maaren and D. van der Spoel, J. Chem. Theory Comput., 2018, 14, 5933–5948.
7. R. J. M. Bindels, Nat. Genet., 2003, 35, 302–303.
8. B. J. Finlayson-Pitts, M. J. Ezell and J. N. Pitts Jr, Nature, 1989, 337, 241–244.
9. T. Utigard, JOM, 1998, 50, 38–43.
10. T. Inoue and L. Koch, Nucl. Eng. Technol., 2008, 40, 183–190.
11. F. Lantelme and H. Groult, Molten salts chemistry: from lab to applications, Newnes, 2013.
12. M. M. Kenisarin, Renewable Sustainable Energy Rev., 2010, 14, 955–970.
13. P. D. Myers, Jr. and D. Y. Goswami, Appl. Therm. Eng., 2016, 109, 889–900.
14. D. H. Kelley and T. Weier, Appl. Mech. Rev., 2018, 70, 020801.
15. H. Kim, D. A. Boysen, J. M. Newhouse, B. L. Spatocco, B. Chung, P. J. Burke, D. J. Bradwell, K. Jiang, A. A. Tomaszowska, K. Wang, W. Wei, L. A. Ortiz, S. A. Barriga, S. M. Poizeau and D. R. Sadoway, Chem. Rev., 2012, 113, 2075–2099.
16. M.-M. Walz and D. van der Spoel, Phys. Chem. Chem. Phys., 2019, 21, 8516–18524.
17. M.-M. Walz and D. van der Spoel, Direct Link Between Structure, Dynamics and Thermodynamics in Molten Salts, submitted.
18. M. Rang and G. Kresse, Phys. Rev. B, 2019, 99, 184103.
19. L. Wang, A. van de Walle and D. Alfe, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 092102.
20. C. R. Gopikrishnan, D. Jose and A. Datta, AIP Adv., 2012, 2, 012131.
21. J. L. Aragones, E. Sanz, C. Valeriani and C. Vega, J. Chem. Phys., 2012, 137, 104507.
22. I. Leontyev, M. Vener, I. Rostov, M. Basilevsky and M. D. Newton, J. Chem. Phys., 2003, 119, 8024–8037.
23. M. Vener, I. Leontyev and M. Basilevsky, J. Chem. Phys., 2003, 119, 8038–8046.
24. I. Leontyev and A. Stuchebrukhov, J. Chem. Phys., 2009, 130, 02B609.
25. I. Leontyev and A. Stuchebrukhov, Phys. Chem. Chem. Phys., 2011, 13, 2613–2626.
26. R. Fuentes-Azcatl and M. C. Barbosa, J. Phys. Chem. B, 2016, 120, 2460–2470.
27. R. Fuentes-Azcatl and M. C. Barbosa, Phys. A, 2018, 491, 480–489.
28. A. Galwey, J. Therm. Anal. Calorim., 2005, 82, 423–437.
29. A. Galwey, J. Therm. Anal. Calorim., 2006, 86, 561–579.
30. A. R. Ubbelohde, The molten state of matter: melting and crystal structure, John Wiley & Sons, 1978.
31. N. March and M. Tosi, J. Phys. Chem. Solids, 1985, 46, 757–760.
32. K. Ksiazek and T. Gorecki, High Temp. Mater. Processes, 1999, 3, 297–310.
33. K. Ksiazek and T. Gorecki, J. Mater. Sci. Lett., 2001, 20, 1623–1625.
34. A. Ladd and L. Woodcock, Chem. Phys. Lett., 1977, 51, 155–159.
35. A. Ladd and L. Woodcock, Mol. Phys., 1978, 36, 611–619.
36. J. R. Morris and X. Song, J. Chem. Phys., 2002, 116, 9352–9358.
37. C. Vega, E. Sanz, J. Abascal and E. Noya, J. Phys.: Condens. Matter, 2008, 20, 153101.
38. S. Martiniani, P. M. Chaikin and D. Levine, Phys. Rev. X, 2019, 9, 011031.
39. I. S. Joung and T. E. Cheatham III, J. Phys. Chem. B, 2008, 112, 9020–9041.
40. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
41. L. X. Dang and D. E. Smith, J. Chem. Phys., 1993, 99, 6950–6956.
42. D. E. Smith and L. X. Dang, J. Chem. Phys., 1994, 100, 3757.
43. M. Tosi and F. Fumi, J. Phys. Chem. Solids, 1964, 25, 45–52.
44. H. W. Horn, W. C. Swope, J. W. Pitera, J. D. Madura, T. J. Dick, G. L. Hura and T. Head-Gordon, J. Chem. Phys., 2004, 120, 9665–9678.
45. H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271.
46. L.-P. Wang, J. Chen and T. V. Voorhis, J. Chem. Theory Comput., 2013, 9, 452–460.
47. W. Hogervorst, Physica, 1971, 51, 77–89.
48. D. Adams and I. McDonald, J. Phys. C: Solid State Phys., 1974, 7, 2761.
49. J. W. Lewis, K. Singer and L. V. Woodcock, J. Chem. Soc., Faraday Trans. 2, 1975, 71, 301–312.
50. G. Ciccotti, G. Jacucci and I. McDonald, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 13, 426.
51. J. Wu, J. Wang, H. Ni, G. Lu and J. Yu, J. Mol. Liq., 2018, 253, 96–112.
52. J. Ding, G. Pan, L. Du, J. Lu, X. Wei, J. Li, W. Wang and J. Yan, Nano Energy, 2017, 39, 380–389.
53. C. Caccamo and M. Dixon, J. Phys. C: Solid State Phys., 1980, 13, 1887.
54. J. Anwar, D. Frenkel and M. G. Noro, J. Chem. Phys., 2003, 118, 728–735.
55. D. B. Sirdeshmukh, L. Sirdeshmukh and K. G. Subhadra, Alkali Halides, Springer, Berlin, Heidelberg, New York, 1st edn, 2001.
56. P. C. Rodrigues and F. M. Silva Fernandes, J. Chem. Phys., 2007, 126, 024503.
57. J. Michielsen, P. Woerlee, F. V. Graaf and J. Ketelaar, J. Chem. Soc., Faraday Trans. 1, 1975, 71, 1730–1741.
58. M. Salanne and P. A. Madden, Mol. Phys., 2011, 109, 2299–2315.
59. A. B. Belonoshko, N. Skorodumova, A. Rosengren and B. Johansson, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 012201.

---

Footnote

† Electronic supplementary information (ESI) available: Further simulation details are described. The determined melting points are tabulated for the WBK and JC (TIP3P-compatible) model, and for reference also experimental values and other simulation results are provided. In addition plots showing the final file size vs. the simulation temperature, the diffusion coefficient vs. the simulation temperature, and the radial distribution functions for the respective temperature are provided for each salt and force field. See DOI: 10.1039/c9cc06177k

---