A facile oxygen-17 NMR method to determine effective viscosity in dilute, molecularly crowded and confined aqueous media

Abstract

We present an NMR method based on natural abundance ¹⁷O relaxation of water to determine effective viscosity in biological aqueous samples. The method accurately captures viscosity of dilute and crowded protein solutions and offers a fairly simple way to quantify the internal fluidity of biological condensates formed through phase separation.

---

Life relies on the spatiotemporal arrangement and coordination of the components and activities of living systems.¹ In cells, the spatial arrangement is provided either through compartmentalization via membranous organelles, or alternatively, through a process termed liquid–liquid phase separation (LLPS) which leads to the formation of membrane-less bodies in cells.² Physical properties of the cellular bodies formed after LLPS exhibit remarkable diversity, ranging from liquid-like droplets to gel-like phases with different degrees of confinement.³ Different micro-rheological and biophysical techniques based on fusion timescale or diffusion analysis are utilized to probe the viscoelastic properties of biological condensates.^4,5 Further progress in characterization of biological phase separation requires developments in experimental methods probing the highly crowded and confined environments inside biological condensates.⁶

Temporal coordination of biological activities depends on the characteristic times of various motional modes of biomolecules,¹ influenced potentially by local concentration and the crowding effect.⁷ Protein dynamics generally occur at multiple time and length scales, which are best characterized through combination of several experimental techniques.^8,9 Due to differences in the inherent sensitivity of various experimental techniques, protein samples at different concentrations are often used for protein dynamical studies. It is therefore essential to quantify pure viscosity effects on protein dynamics before any reasonable comparison of experimental data obtained at different protein concentrations can be made.

It has been suggested that water dynamics could be used as a reliable proxy for the local viscosity.¹⁰ One of the best methods to study water dynamics is ¹⁷O NMR.¹¹¹⁷O nucleus has spin quantum number I of 5/2 and natural abundance of 0.037%. The dominant NMR relaxation mechanism of ¹⁷O is the anisotropic interaction between the quadrupole moment (Q) of ¹⁷O and the electric field gradient present at the site of ¹⁷O nuclei.¹² Here, we utilize ¹⁷O longitudinal relaxation (R₁) rate of water, essentially a probe of water structure and dynamics, to determine effective viscosity in biological aqueous samples behaving as Newtonian fluids. Effective viscosity is a local microscopic property of solutions influencing Brownian diffusion of solutes. In non-homogeneous (crowded) solutions, the effective viscosity experienced by the rotationally diffusing solutes may be significantly different from the bulk viscosity.¹³

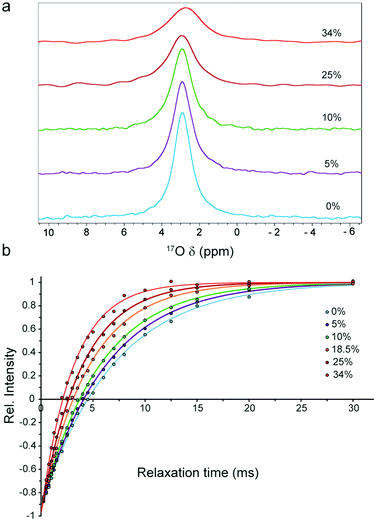
First, we investigated the viscosity dependence of ¹⁷O R₁ rate of water in glycerol–water mixtures, for which the solution viscosities are well known¹⁴ and diffusion obeys the classical Stokes laws.¹³ The ¹⁷O NMR experiments were performed for samples containing 0 to 34% (v/v) glycerol, in which the solution viscosity at 298 K varied from 0.89 to 3.01 cP. In 1D ¹⁷O spectra, the intensity of water signal changed in proportion to water content (Fig. S1, ESI†). In addition, the signal linewidths rose from 46.5 ± 0.1 Hz at 0% glycerol to 101.8 ± 0.3 Hz at 34% glycerol, reflecting the increase in viscosity and its resultant signal broadening (Fig. 1a). Similarly, the ¹⁷O R₁ rates followed an increasing trend from 145 ± 4 s⁻¹ at 0% glycerol to 323 ± 9 s⁻¹ at 34% glycerol (Fig. 1b and Fig. S2, ESI†). The value obtained at 0% glycerol is in excellent agreement with previous reports,¹⁵ and implicates a rotational correlation time (τ_rot) of 1.54 ± 0.04 ps for water molecules in accord with earlier studies.^15–17

Fig. 1 ¹⁷O NMR relaxation of water in water–glycerol mixtures, in dependence of glycerol concentration (v/v, %). (a) 1D ¹⁷O spectra, showing glycerol concentration-dependent broadening of water ¹⁷O signals. (b) ¹⁷O longitudinal relaxation rate (R₁) of water, measured through inversion-recovery experiments. Relative intensities of water ¹⁷O signals are shown as a function of recovery time. Faster recovery indicates larger R₁ rates.

Besides increasing viscosity and its resultant effect on τ_rot of water molecules, addition of glycerol may alter the hydrogen-bonded network structure of water and thereby modulate the quadrupole coupling constant (χ) and asymmetry (η) of water ¹⁷O nuclei. To our knowledge, there is no report in the literature concerning the quadrupole parameters of water ¹⁷O in glycerol–water mixtures, except in the frozen state, where ¹⁷O parameters of water are not significantly affected by 60% glycerol.¹⁸ Thus, it has been shown that the quadrupole coupling factor, χ²(1 + η²/3), of water ¹⁷O changes only minimally over a broad range of temperatures from 274 to 350 K (ca. 6%), where the hydrogen bond network of water undergoes significant alterations.¹⁶ Consequently, we assume that the change in quadrupole coupling factor of water ¹⁷O over the studied range of glycerol concentrations remains negligibly small for the purpose of current study. Based on this assumption, the τ_rot of water increases to ∼1.7, 1.9, 2.3, 2.7 and 3.4 ps, respectively at 5, 10, 18.5, 25 and 34% glycerol concentration. It is interesting to note that the change in water dynamics upon addition of glycerol is less prominent when compared to solution viscosity (Fig. S3, ESI†). Contrary to the τ_rot of water molecules which is supposedly linearly related to ¹⁷O R₁ rates, the solution viscosity versus¹⁷O R₁ data showed better fit to a quadratic function when compared to a linear function (p-value < 0.001). The obtained empirical function was:

η (cp) = 1.719 (±0.194) × 10⁻⁵ × (R₁)² + 0.004 (±0.001) × R₁ − 0.065 (±0.017) (1)

which can be used in determination of viscosity in aqueous solutions at 298 K. Similar quadratic relations were observed at 310 K, and to a less degree, at 288 K (Fig. S4, ESI†).

Next, the temperature dependence of ¹⁷O R₁ rate of water was studied in pure water, for which the temperature dependence of viscosity is well established.¹⁹ Upon a decrease from 310 K to 275.4 K, the ¹⁷O R₁ rate increased from 107 ± 6 s⁻¹ to 385 ± 14 s⁻¹ (Fig. S5a, ESI†). The increase in ¹⁷O R₁ rates upon cooling is expected because of the longer τ_rot of water at lower temperatures. This effect is however partially counteracted by the small albeit considerable drop in ¹⁷O quadrupole coupling factor of water at low temperatures.¹⁶ Taking the temperature dependence of the quadrupole coupling factor into consideration, the τ_rot of water changes from 1.12 ± 0.06 ps at 310 K to 4.16 ± 0.16 ps at 275.4 K. The relation between viscosity/temperature (η/T) ratio and ¹⁷O R₁ rates deviated from linearity and was better represented by a quadratic function (p-value < 0.001, Fig. S5b, ESI†). The observed deviations from linearity, both in water–glycerol mixtures and in pure water over the studied temperature range, suggest that the effect of perturbation on solution viscosity cannot be well approximated to a first-order change in the dynamics of individual water molecules.

With the viscosity and temperature dependence of ¹⁷O R₁ rate of water established, we employed ¹⁷O R₁ rates to evaluate effective viscosity (henceforth viscosity) in a number of test cases. First, we investigated aqueous solutions containing high protein concentration, such as 4 mM ubiquitin and 3 mM GB3. At 298 K, the ¹⁷O R₁ rates were 164 ± 3 and 153 ± 4 s⁻¹, respectively, which using eqn (1), corresponded to viscosities of 1.07 ± 0.03 and 0.96 ± 0.03 cP. The η_protein/η_water ratio was ∼1.20 ± 0.03 for 4 mM ubiquitin and 1.08 ± 0.04 for 3 mM GB3 solutions, in close agreement with the viscosity ratios of ∼1.17 and 1.08 predicted on the basis of volume occupancies (see ESI†). Then, the rotational correlation time (τ_c) of ubiquitin and GB3 were determined through ¹⁵N cross-correlated relaxation (CCR) rates. At 4 mM concentration, the average CCR rate of ubiquitin was 4.83 ± 0.05 s⁻¹, corresponding to a τ_c of 4.82 ± 0.04 ns. Compared to the τ_c of ubiquitin at much lower concentration of 0.37 mM (see below, also ref. 20), the τ_c of ubiquitin at 4 mM concentration exhibited an increase by a factor of 1.20 ± 0.02. The increase in τ_c of ubiquitin closely matches the observed viscosity ratio obtained above. This finding is interesting as it rules out significant dimerization of ubiquitin at such a high concentration, as previously suggested.²¹ For GB3, the average CCR rate was 3.82 ± 0.03 s⁻¹, corresponding to a τ_c of 3.47 ± 0.04 ns (Fig. S6, ESI†), slightly larger than the value of 3.35 ± 0.03 ns reported at 2 mM GB3 concentration.²² Considering the expected 8% change in viscosity, the τ_c of GB3 at infinite dilution would be ∼3.23 ns, implying a rather small atomic effective radius (AER) value of ∼2.5 Å for hydrodynamic calculations. Taken together, the ¹⁷O R₁ measurement of bulk water allowed quantification of viscosity changes at high-concentration protein samples and enabled estimating alterations in the τ_c of proteins.

Second, we studied molecularly crowded aqueous solutions mimicking the environment of interior of cells.⁷ To address how crowding agents alter the solution viscosity, we examined two commonly used neutral polymeric crowding agents: Ficoll 70 and sucrose. At 200 g L⁻¹ concentration of Ficoll 70, the ¹⁷O R₁ rate of water was 247 ± 5 s⁻¹, which using eqn (1), corresponded to a viscosity of 2.00 ± 0.07 cP and the η_Ficoll/η_water ratio of 2.23 ± 0.12 (Fig. 2 and Fig. S7, ESI†). Similarly, the ¹⁷O R₁ rate of water at 200 g L⁻¹ sucrose was 207 ± 7 s⁻¹, corresponding to the viscosity of 1.52 ± 0.08 cP and η_sucrose/η_water ratio of 1.70 ± 0.11. Assuming that the quadrupole parameters of water ¹⁷O remained effectively unperturbed, the τ_rot of water molecules were 2.62 ± 0.04 ps in Ficoll 70 and 2.19 ± 0.05 ps in sucrose solutions. To further evaluate the ¹⁷O R₁-based viscosities, we employed ¹⁵N relaxation rates R₁ and R₂, as reported in ref. 20, and determined τ_c of the ¹⁵N-labelled ubiquitin in dilute and crowded samples. The τ_c of ubiquitin calculated from residue-specific ¹⁵N R₂/R₁ ratios were 3.98 ± 0.30 ns in dilute solution, 9.06 ± 0.84 ns in 200 g L⁻¹ Ficoll 70 and 7.50 ± 0.69 ns in 200 g L⁻¹ sucrose (Fig. S8, ESI†). Interestingly, the τ_c,Ficoll/τ_c,water of 2.31 ± 0.05 was in agreement with the viscosity ratio of 2.23 ± 0.12 obtained through ¹⁷O R₁ rates (Fig. 2). The τ_c,sucrose/τ_c,water of 1.88 ± 0.04 was however slightly larger than the ¹⁷O R₁-based viscosity ratio of 1.70 ± 0.11. Overall, the method based on ¹⁷O R₁ rates of water provided a fairly accurate value of viscosity in crowded solutions.

Fig. 2 Solution viscosity in crowded media, as probed by ¹⁷O longitudinal relaxation rate (R₁) of water and rotational correlation time (τ_c) of ubiquitin. Residue-specific τ_c of ubiquitin in dilute and crowded solutions are reported as the ratio of τ_c,crowded/τ_c,dilute. The corresponding viscosity ratios obtained through ¹⁷O R₁ of water are shown as solid (average) and dashed (±SD) lines.

Third, we examined confined aqueous media such as biological hydrogels. To investigate whether the ¹⁷O R₁ of water could be used as a proxy to monitor the confinement level inside biological hydrogels, we first examined gels formed at different agarose concentrations. The ¹⁷O R₁ rate of water increased from 150 ± 4 s⁻¹ at 0.5% agarose gel to 156 ± 3, 160 ± 4 and 173 ± 4 s⁻¹, respectively, at 1%, 1.5% and 2% agarose gels (Fig. S9, ESI†). The τ_rot of water molecules is expected to undergo a similar rising trend from 1.59 ± 0.04 ps to 1.65 ± 0.03, 1.69 ± 0.04 and 1.84 ± 0.04 ps, in accord with the increasing level of confinement in dependence of agarose concentration.

Subsequently, we examined a thermo-responsive Ile-Phe dipeptide-based hydrogel.²³ Interestingly, the ¹⁷O R₁ rate of water in the Ile-Phe gel was 184 ± 3 s⁻¹, even bigger than that of 2% agarose (Fig. 3). The large ¹⁷O R₁ of water in Ile-Phe hydrogel may have its origin in the large level of confinement, or alternatively, be caused by the presence of residual alcohol (HFiP) within the gel and its impact on local viscosity.

Fig. 3 Water dynamics in the confined media of biological hydrogels, as probed by ¹⁷O longitudinal relaxation rate (R₁) of water. ¹⁷O R₁ of water in agarose, Ile-Phe and FG peptide-based hydrogels are compared.

Finally, we measured ¹⁷O R₁ of water in a gel-forming FG-based peptide, part of the nuclear pore complex.²⁴ At 1.6 mM peptide concentration, the ¹⁷O R₁ rate of water in the formed hydrogel was 147 ± 2 s⁻¹, between the values observed in water and in 0.5% agarose gel. The ¹⁷O R₁ rate of water exhibited a concentration-dependent increase to 154 ± 2 s⁻¹ at 8 mM and 166 ± 3 s⁻¹ at ∼ 20 mM FG peptide concentration (Fig. 3). The corresponding τ_rot of water were 1.55 ± 0.02, 1.63 ± 0.02 and 1.76 ± 0.04 ps, reflecting slight restriction of water dynamics within the hydrogel in dependence of FG peptide concentration. The level of mobility restriction in 1.6, 8 and 20 mM FG peptide concentration hydrogels is similar to <0.5%, 1% and 1.5–2% agarose gels, respectively. Taken together, the ¹⁷O R₁ of water was capable of capturing differences in the confinement level of agarose and peptide-based hydrogels.

The ¹⁷O R₁-based method presented above offers a simple and quick way for determination of viscosity in biological aqueous samples. Despite the very low natural abundance of ¹⁷O and its low gyromagnetic ratio, the presented method is not particularly demanding in terms of sample requirements or magnetic fields. At 9.4 T magnetic field corresponding to proton Larmor frequency of 400.13 MHz, the ¹⁷O R₁ experiment of a typical sample required 3–4 hours of measurement. This is because of the high concentration of water and fairly high mobility of water molecules, even in environments as confined as 2% agarose gel studied above. Compared to the alternative methods of viscosity determination in crowded cellular or confined media, such as NMR line width analysis,²⁵ or ¹⁹F NMR- or fluorescence-based analysis of rotational and translational diffusion,^5,26 the method based on natural abundance ¹⁷O relaxation of water is advantageous as it does not require additional labelling or external probes, and is relatively immune to transient protein–protein interactions ubiquitous in cellular media.

The ¹⁷O relaxation rate of water is sensitive not only to the τ_rot of water molecules, but also to the quadrupole coupling factor of H₂¹⁷O.¹⁶ As a result, the use of ¹⁷O R₁ rates of water in viscosity determination is in principle limited to the cases in which changes in water structure and consequently in the quadrupole coupling factor of H₂¹⁷O are negligibly small. Theoretical and experimental investigations suggest that the above condition is indeed not very stringent and can be met over a wide range of temperatures and possible hydrogen-bonded network structures of water.¹⁶ Another potential limitation arises when ¹⁷O relaxation of water is altered by paramagnetic relaxation effects. Consequently, the presented method cannot be applied to samples in which the presence of a paramagnetic component (such as Cu²⁺ or Mn²⁺) cannot be avoided. Moreover, to eliminate unwanted paramagnetic ions and dissolved molecular oxygen, it is essential to use deionized water and degas the samples before NMR experiments.

NMR spin relaxation is a powerful technique to probe protein dynamics at atomistic resolution. NMR-based dynamical studies are frequently performed at high protein concentrations, where concentration-dependent changes in viscosity influence the timescale of different motional modes of proteins. In particular, low-field proton relaxometry, a powerful technique monitoring slow reorientational dynamics in disordered proteins,⁹ requires millimolar protein concentrations. As exemplified by the ubiquitin and GB3 data above, the viscosity determination through ¹⁷O R₁ of water enables direct evaluation of the viscosity effects on protein dynamics and allows disentangling pure viscosity effects from potential concentration-dependent phenomena such as protein self-association events. In addition, NMR experiments in non-standard conditions such as crowded media, super-cooled temperatures and high hydrostatic pressures can benefit from direct viscosity determination.²⁷

The traffic between cell nucleus and cytoplasm is controlled via gel forming FG-rich domains of nucleoporins.²⁴ For the FG peptide used in this study, the hydrogel formed at low peptide concentration showed ¹⁷O R₁ of water only slightly larger than the bulk water, suggesting that the dynamics of water within the channels of the FG hydrogel were largely unaffected. On the other hand, the ¹⁷O R₁ of water in the high-concentration FG hydrogel was comparable to 1.5–2% agarose gel, indicating a considerable level of water mobility restriction. We suggest that the ¹⁷O R₁ of water can be used as a proxy to monitor changes in the local environment of biological hydrogels.

In summary, a facile ¹⁷O NMR method to determine effective viscosity in biological samples is presented. The method captures effective viscosity in dependence of protein concentration and crowding, and is capable of reporting the confinement level in biological hydrogels, therefore has the potential to be utilized in quantitative characterization of biological condensates in the rapidly growing fields of phase separation and peptide-based pharmaceutical hydrogels.

N. R.-G. acknowledges German Research Foundation (DFG) for a research grant (RE 3655/2-1). The FG peptide was kindly provided by Dirk Görlich. Open Access funding provided by the Max Planck Society.

Conflicts of interest

There are no conflicts to declare.

References

1. P. Machamer, L. Darden and C. F. Craver, Philos. Sci., 2000, 67, 1–25.
2. S. F. Banani, H. O. Lee, A. A. Hyman and M. K. Rosen, Nat. Rev. Mol. Cell Biol., 2017, 18, 285–298.
3. S. Alberti, Curr. Biol., 2017, 27, R1097–R1102.
4. S. Elbaum-Garfinkle, Y. Kim, K. Szczepaniak, C. C. Chen, C. R. Eckmann, S. Myong and C. P. Brangwynne, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7189–7194.
5. J. Wang, J. M. Choi, A. S. Holehouse, H. O. Lee, X. Zhang, M. Jahnel, S. Maharana, R. Lemaitre, A. Pozniakovsky, D. Drechsel, I. Poser, R. V. Pappu, S. Alberti and A. A. Hyman, Cell, 2018, 174(688–699), e616.
6. S. Alberti, A. Gladfelter and T. Mittag, Cell, 2019, 176, 419–434.
7. G. Rivas and A. P. Minton, Trends Biochem. Sci., 2016, 41, 970–981.
8. N. Salvi, A. Abyzov and M. Blackledge, J. Phys. Chem. Lett., 2016, 2483–2489.
9. N. Rezaei-Ghaleh, G. Parigi, A. Soranno, A. Holla, S. Becker, B. Schuler, C. Luchinat and M. Zweckstetter, Angew. Chem., Int. Ed., 2018, 57, 15262–15266.
10. B. Halle and M. Davidovic, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 12135–12140.
11. J. Qvist, E. Persson, C. Mattea and B. Halle, Faraday Discuss., 2009, 141, 131–144 ; discussion 175–207.
12. I. P. Gerothanassis, Prog. Nucl. Magn. Reson. Spectrosc., 2010, 56, 95–197.
13. C. Li, Y. Wang and G. J. Pielak, J. Phys. Chem. B, 2009, 113, 13390–13392.
14. A. Volk and C. J. Kahler, Exp. Fluids, 2018, 59, 75.
15. D. Lankohrst, J. Schriever and J. C. Leyte, Ber. Bunsenges. Phys. Chem., 1982, 86, 215–221.
16. J. Ropp, C. Lawrence, T. C. Farrar and J. L. Skinner, J. Am. Chem. Soc., 2001, 123, 8047–8052.
17. K. Modig and B. Halle, J. Am. Chem. Soc., 2002, 124, 12031–12041.
18. V. K. Michaelis, B. Corzilius, A. A. Smith and R. G. Griffin, J. Phys. Chem. B, 2013, 117, 14894–14906.
19. R. C. Weast, Handbook of Chemistry and Physics, CRC Press, West Palm Beach, FL, 1978.
20. F. Munari, A. Bortot, S. Zanzoni, M. D'Onofrio, D. Fushman and M. Assfalg, FEBS Lett., 2017, 591, 979–990.
21. Z. Liu, W. P. Zhang, Q. Xing, X. Ren, M. Liu and C. Tang, Angew. Chem., Int. Ed., 2012, 51, 469–472.
22. J. B. Hall and D. Fushman, J. Biomol. NMR, 2003, 27, 261–275.
23. N. S. de Groot, T. Parella, F. X. Aviles, J. Vendrell and S. Ventura, Biophys. J., 2007, 92, 1732–1741.
24. B. B. Hulsmann, A. A. Labokha and D. Gorlich, Cell, 2012, 150, 738–751.
25. Q. Wang, A. Zhuravleva and L. M. Gierasch, Biochemistry, 2011, 50, 9225–9236.
26. Y. Ye, X. Liu, Z. Zhang, Q. Wu, B. Jiang, L. Jiang, X. Zhang, M. Liu, G. J. Pielak and C. Li, Chem. – Eur. J., 2013, 19, 12705–12710.
27. L. P. Singh, B. Issenmann and F. Caupin, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 4312–4317.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental methods and supplementary figures. See DOI: 10.1039/c9cc06124j

---