Superlattices based on van der Waals 2D materials

Abstract

Two-dimensional (2D) materials exhibit a number of improved mechanical, optical, and electronic properties compared to their bulk counterparts. The absence of dangling bonds in the cleaved surfaces of these materials allows combining different 2D materials into van der Waals heterostructures to fabricate p-n junctions, photodetectors, and 2D–2D ohmic contacts that show unexpected performances. These intriguing results are regularly summarized in comprehensive reviews. A strategy to tailor their properties even further and to observe novel quantum phenomena consists in the fabrication of superlattices whose unit cell is formed either by two dissimilar 2D materials or by a 2D material subjected to a periodic perturbation, each component contributing with different characteristics. Furthermore, in a 2D material-based superlattice, the interlayer interaction between the layers mediated by van der Waals forces constitutes a key parameter to tune the global properties of the superlattice. The above-mentioned factors reflect the potential to devise countless combinations of van der Waals 2D material-based superlattices. In the present feature article, we explain in detail the state-of-the-art of 2D material-based superlattices and describe the different methods to fabricate them, classified as vertical stacking, intercalation with atoms or molecules, moiré patterning, strain engineering and lithographic design. We also aim to highlight some of the specific applications of each type of superlattices.

---

From left to right: Andres Castellanos-Gomez, Yu Kyoung Ryu and Riccardo Frisenda

Our lab is part of the 2D Foundry, a research group of the Instituto de Ciencia de Materiales de Madrid (which is part of the Spanish National Research Council, Consejo Superior de Investigaciones Científicas). Our research focusses on the exploration of novel 2D materials and the use of strain engineering to modify their properties. Through the fabrication of optoelectronic nanodevices based on 2D materials, heterostructures and superlattices we probe the electronic, mechanical and optical properties of these nanomaterials. We also devote a fraction of our research time to develop experimental techniques and cost-effective tools to make 2D materials research more accessible and widespread.

1. Introduction

In their Communication (1970), IBM researchers Esaki and Tsu envisioned theoretically the realization of a novel semiconductor structure,¹ either by a periodic variation of the doping level in a single material or by a periodic variation of two dissimilar materials. They claimed that if the period of such structures was shorter than the electron mean free path, it would be possible to observe new quantum confinement phenomena, due to the opening of extra allowed and forbidden energy bands, not available in a traditional device. They coined this novel device with a periodic potential as “superlattice”. Shortly after, Esaki and Chang demonstrated quantum transport states in a 50-period GaAs–AlAs superlattice fabricated by molecular-beam epitaxy.² Later, Osbourn introduced strain-engineering as a new variable to modulate the bandgap in a superlattice by controlling the growth of alternative layers with a certain lattice mismatch.³ In these pioneering works, the authors had predicted that the experimental evolution of superlattices would mean the opening of new fields in semiconductor research. Since then, the semiconductor industry has developed standard fabrication methods to obtain superlattices from conventional 3D semiconducting materials through molecular beam epitaxy, sputtering or other vacuum deposition methods.^4–6 These conventional superlattices have reached a limitation in their thermoelectric, optoelectronic, and energy-storage performance that does not meet the current needs of the society. On this basis, the nanowires, due to their reduced dimensions and high surface-to-volume ratio, are being considered as new building blocks for the next generation of superlattices.^7–9 Nevertheless, the control over the interface states to obtain an optimal, abrupt junction is difficult due to the covalent nature of most of the nanowire heterojunctions and the presence of dangling bonds in their surface.¹⁰

The isolation of 2D materials by mechanical or chemical exfoliation of bulk van der Waals materials and the synthesis of ultrathin van der Waals layered materials have changed one step further the paradigm in the fabrication of superlattices. 2D materials are atomically thin and have an area on the order of hundreds of microns square. This trait endows them with an extremely high surface-to-volume ratio. The surface of these materials is devoid of dangling bonds and their heterostructures are held by van der Waals forces. As a result of these features, 2D materials have shown extraordinary physical and chemical properties. This has motivated the synthesis of novel 2D nanomaterials such as ultrathin metal–organic framework layers,¹¹ transition metal oxides and hydroxides¹² or covalent-organic framework layers,^13,14 in order to obtain enhanced chemical reactivity and device performance in comparison to their 3D, covalent homologues. This wide variety of 2D nanomaterials and available methods to prepare them open the door to the emerging field of van der Waals superlattices. Starting with 2D materials as the building blocks, periodic potentials from structures with precise atomic resolution can be now easily achieved, even without the need of vacuum deposition techniques. The exploration of superlattices based on van der Waals 2D materials, both theoretically and experimentally, has barely started. However, there exists already a solid body of results that contributes to settle down the bases of the field. These results are the focus of the present feature article, divided into the main 2D based superlattice types shown in Table 1:

Table 1 Type of van der Waals 2D material superlattice (first column), scheme of the elements that compose their unit cell (second column), mechanisms to modulate the superlattice for each type (third column) and their applications found in the literature up to now (fourth column)

Classification	Elements of the unit cell	Modulation by (dimension)	Applications (ref.)
Vertical stacking		Chemical composition, lattice (mis)match (1D)	• IR photodetectors^15,16,20
			• Phase-change memory^28–34
			• Thermoelectrics^47–50
			• Superconductivity^51–54
Intercalated compounds		Chemical composition, structuring, charge transfer (1D)	• Optoelectronics^55–61,72–75
			• Superconductivity^62
			• Thermoelectrics^63,64
			• Energy storage^67–71
Moiré periodic patterns		Atom rearrangement, misorientation angle, strain (2D)	• Dirac point states^87,95–99
			• Hofstadter's butterfly^89–94
			• Superconductivity^100–106
			• Moiré interlayer excitons^107–109
Strain engineered		Periodic in-plane or out-of-plane strain (1D or 2D)	• Phase-change memory^117,118
			• Bandgap engineering^119–122
			• Optoelectronics^125,126
Lithographic engineered		Dielectric patterning, periodic substrate, periodic patterning, strain (1D or 2D)	• Artificial crystals^128–130
			• Moiré periodicities^131
			• Bandgap engineering^132,133

---

(1) Vertical stacking of dissimilar 2D layers, where the periodic potential is modulated principally by the chemical composition of the layers and/or the lattice mismatch existing between them.

(2) Multi-layered 2D materials that are subjected to an intercalation process. In this type of superlattices, the periodic potential can be modulated by the chemical composition of the layers, the re-structuration of the functionalized layers after the intercalation of the hosting species and the charge transfer that takes place between the host flakes and the atoms or molecules.

(3) Moiré structures by twisting of two 2D material-based layers. When two equivalent (e.g. graphene bilayer) or dissimilar (e.g. graphene/h-BN) adjacent layers are rotated under certain angles, the lattice mismatch and/or the atom rearrangement give rise to moiré-pattern superlattices with new lattice periodicities.

(4) Strain-engineered layers. A periodic potential can be produced by subjecting a 2D material flake to periodic tensile/compressive strains or by introducing a periodic, controlled mismatch between the lattices of two dissimilar 2D materials.

(5) Synthetic superlattices defined by lithography. In this approach, the periodic potential can be induced in a 2D material by placing it on a patterned topography or by patterning the material itself with a lithographic technique.

Note that in some cases there is more than one single mechanism involved in the fabrication of the superstructure. Specifically, either as an explicit parameter or produced unintentionally, strain is found to have an important role in the modulation of electronic/optical properties in most of the other types of superlattices.

Each type of superlattice (1 to 5) and its potential applications will be discussed in detail in the next section and the corresponding subsections.

2. 2D material superlattices

2.1 Vertically stacked superlattices

2.1.1 Naturally occurring superlattices. Natural van der Waals superlattices have been obtained by isolating thin layers from minerals such as franckeite^15–19 or cylindrite.²⁰ Both minerals belong to the family of sulfosalts with the general formula (Pb,Sn)_6+x²⁺Sb₂³⁺Fe²⁺Sn₂⁴⁺S_14+x, with −1 ≤ x ≤ 0.25.²¹ Franckeite constitutes a natural misfit compound mineral, whose superlattice structure has been formed by alternating phase segregation of pseudo-hexagonal Sn-rich and pseudo-tetragonal Pb-rich layers, separated by a van der Waals gap (Fig. 1(a)). The electrical characterization of exfoliated flakes from this material shows that it is a highly p-type doped semiconductor with a narrow bandgap (<0.7 eV), which is suitable for infrared (IR) detection.^15,16 In the case of cylindrite, thin flakes were obtained from mechanical or liquid phase exfoliation. The characterization by high-resolution TEM images showed that the cylindrite thin flakes were composed of a stack of alternating pseudo-tetragonal Pb-rich and octahedral Sn-rich layers. Analogous to the franckeite thin layers, the thin cylindrite layer-based field-effect transistors behaved as a highly p-type doped semiconductor with a narrow bandgap (< 0.85 eV), suitable to measure photoresponse in the IR. The characterization of the magnetic properties of the thin flakes proved that the intrinsic magnetic interactions present in the bulk mineral are preserved after thinning.²⁰ Both minerals have the advantage of being stable under ambient conditions. These results underline the existence of more natural minerals from which thin layers with novel properties can be isolated.

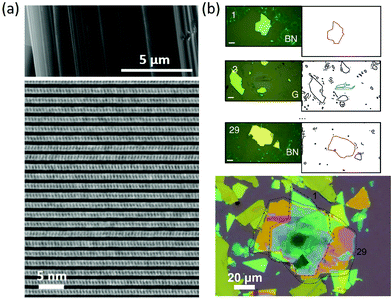Fig. 1 (a) SEM image of an exfoliated franckeite showing the layered nature of the mineral (top). Cross-sectional TEM image of the superlattice viewed along the [100] direction. Reproduced with permission from ref. 5. (b) Artificial van der Waals superlattice comprising 29 alternating layers of graphite and h-BN. Top: Optical microscope images of some of the graphite (G) and BN flakes utilized to assemble the superlattice (left) and the vector-drawing line-edges of the flakes automatically extracted from the optical microscope images. The scale bars correspond to 20 μm. Bottom: Optical image of the G/BN superlattice. The dashed lines highlight the bottom and top BN flakes. Reproduced with permission from ref. 12.

2.1.2 Artificial stacking. The fabrication of van der Waals 2D material superlattices by artificial stacking presents the advantage of choosing the materials and piling them up with an optimized interlayer interface to achieve specific optoelectronic properties. Kang et al. developed a large-scale layer-by-layer vertical assembly process.²² The authors achieved a large-area superlattice composed of nine alternating layers of MoS₂ and WS₂ prepared by sequentially peeling with a thermal release tape and stacking the layers under vacuum. They showed the ease of detachment of this superlattice by peeling it off from the substrate in water. In order to pave the way to manufacture complex superlattices with good quality and minimum time and human operation cost, an autonomous robotic assembly system was developed recently by Masubuchi, Machida and co-workers.²³ The localization, shape and thickness of exfoliated 2D materials are the factors that must be taken into account to select and fabricate useful heterostructure devices. The authors estimated the time needed to fabricate manually a 29-layered superlattice in about 120 h of uninterrupted processing. Their system consisting of an automatic scanning of the flakes by using an optical microscope, recording of the position and geometry of the flakes by a computer-assisted design algorithm database and robotic stamp assembling achieved the alternating 29-layered graphene/h-BN superlattice in less than 32 h, with a human operation time less than 6 h (Fig. 1(b)). Both works address the challenges of large-scale production and development of cost-effective manufacturing processes for moving the 2D-material based devices to the industry level.

2.1.3 van der Waals epitaxially grown superlattices. Molecular beam epitaxy is a high-vacuum, low deposition rate technique that is employed to grow semiconductor heterostructures, which present atomically smooth and abrupt interfaces. Due to these reasons, it is also being used to fabricate high-quality 2D material-based superlattices where the different epi-layers are upheld by van der Waals forces.²⁴ Moreover, since the 2D crystalline layers do not present dangling bonds, each epi-layer grows without having to accommodate its lattice constant to that of the layer below. Therefore, some authors define the MBE on 2D materials as van der Waals epitaxy.^25,26 Hereafter, we detail the results achieved by both methods. Epitaxial growth methods allow the precise designing of the transport properties as a function of the chemical composition and thickness of the layers that constitute the superlattice. Recently, by reducing the thickness of the Bi₂Se₃ topological insulating layer in a Bi₂Se₃–In₂Se₃ superlattice from (Bi₂Se₃)₁₂/(In₂Se₃)₆ to (Bi₂Se₃)₆/(In₂Se₃)₆, the transport dimensionality was tuned from coherent 3D to incoherent 2D transport, respectively.²⁷

Interfacial phase-change memory materials that encompass the family of superlattices with the general formula [(GeTe)_x/(Sb₂Te₃)_y]_n are being studied to achieve fast switching and low energy consumption for non-volatile memory applications.²⁸ The TEM characterization of GeTe/Sb₂Te₃ superlattices fabricated by MBE and annealed at 400 °C revealed a reorganization of the superlattice structure into Sb₂Te₃ and GeSbTe rhombohedral layers.²⁹ The prediction of the authors about modulating the electrical, thermal or magnetic properties by controlling the MBE process in this kind of materials was accomplished by Cecchi et al.³⁰ The authors fabricated by molecular beam epitaxy Sb₂Te₃/Ge_xSb₂Te_3+x superlattices. They observed that this configuration reduced the intermixing of the layers compared to the standard GeTe/Sb₂Te₃ superlattices fabricated in the previous work.²⁹ As a consequence, superlattices with less defective, sharper interfaces and higher carrier mobility were achieved. Another epitaxial method, radio-frequency sputtering, has been employed to fabricate interfacial phase-change memory superlattices in several works.^31–34 Particularly, the phase change from a Dirac semimetal to a topological insulator as a function of the thickness of the GeTe layer has been observed, which is promising for spintronic applications.³⁴

In the case of natural minerals such as franckeite^15,16 and cylindrite,²⁰ it was shown how the alternating formation of layers with dissimilar lattice symmetry gives rise to superlattices that grow with a mismatch, but are ordered and thermodynamically stable. This type of materials, called misfit layer compounds, can be synthesized with controlled properties as well. Their general formula is [(MX)_1+δ]_m(TX₂)_n, where M = Sn, Pb, Bi, Sb, rare earths; T = Ti, V, Nb, Ta, Cr; and X = S or Se.^35,36 There is a variant of misfit layer compounds that is metastable and exhibits a turbostratic or rotational disorder along the c-axis, called ferecrystals. These materials present the general formula [(MX)_1+δ]_m(TX₂)_n, where M = Sn, Pb, Bi, La; T = Ti, V, Nb, Ta, Cr, Mo, W; and X = S, Se or Te.^35–38 In both formulas, the coefficients m and n represent the number of layers of each material per unit cell. In a misfit layer compound, there is only one axis of the layers that presents an incommensurate crystallographic direction (Fig. 2(a), left, from ref. 36), while both in-plane axes of the layers in a ferecrystal are incommensurate and independent of each other (Fig. 2(a), right, from ref. 36). The dimensionality (m layers of material 1 and n layers of material 2 per unit cell, i.e. their ratio m/n) of these materials is taken into account to control the properties of both materials: the electrical transport,^39–41 the charge transfer between the layers^42,43 or the presence/strength of a charge density wave state.⁴⁴ Another strategy followed to modulate the electrical properties is by substitution or doping in specific sites of the layers.^45–47

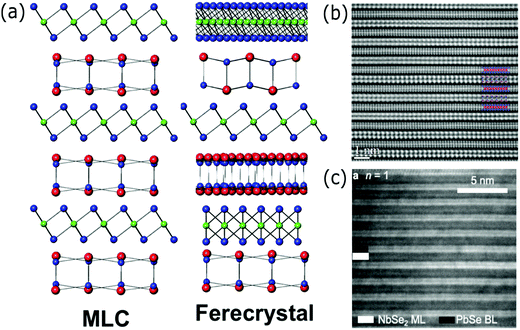Fig. 2 (a) Scheme of the superlattice structure of a misfit layered compound (MLC, left) and a ferecrystal (right). Reproduced with permission from ref. 25. (b) High resolution TEM image of a (SnSe)_1.16(NbSe₂) MLC superconducting superlattice, viewed along the [010] direction. The inset is a scheme of the SnSe/NbSe₂ layers. Reproduced with permission from ref. 40. (c) Cross-sectional TEM image of a (PbSe)_1.14(NbSe₂)_n ferecrystal superconducting superlattice with n = 1. Reproduced with permission from ref. 42.

Both misfit layer compounds and ferecrystals present a high potential in thermoelectric applications because their structure is ideal to develop phonon glass/electron crystal responses, where dichalcogenide layers with high electrical mobility constitute the electron crystal component while the mismatch or turbostratic disorder along the c-axis lowers the lattice thermal conductivity, acting as the phonon glass.^36,48,49 The recent work by Li et al.⁵⁰ demonstrated the influence of the cross-plane thermoelectric properties as a function of the thickness of the layers that formed a misfit layer compound superlattice. The authors measured devices based on (SnSe)_n(TiSe₂)_n, varying the number of layers by n = 1, 3, 4, 5, but keeping the same global stoichiometry. They observed a quasi-linear increase in the cross-plane Seebeck coefficient from −2.5 to −31 μV K⁻¹ as a function of n, and an approximately constant in-plane Seebeck coefficient for different values of n. Another strategy to improve the thermoelectric properties has been the Cu- and Co-substitution of Ti-sites in the TiS₂ layers of a (SnS)_1.2(TiS₂)₂ misfit-layered compound. An increase of the ZT value up to 33.3% in (SnS)_1.2(Cu_0.02Ti_0.98S₂)₂ was obtained compared to the pristine misfit layer compound. This improvement of the figure of merit was explained in terms of the increase in the effective mass and the decrease in the carrier concentration induced by Cu incorporation and the decrease in the thermal conductivity induced by the disorder inherent to the misfit layer compound structuring.⁴⁷

Superconductivity is another application barely explored yet in both misfit layer compounds and ferecrystals. Superconductivity in the synthesized misfit layer compounds (SnSe)_1.16(NbSe₂)⁵¹ and (SnS)_1.15(TaS₂)⁵² with critical temperatures (T_c) of, respectively, 3.4 and 3.01 K was recently reported. In the (PbSe)_1.14(NbSe₂)_n ferecrystal,⁵³ the shift of T_c from 2.66 (n = 3), 1.91 (n = 2) and 1.11 (n = 1) K was observed. The authors studied the reduction of the transition temperature as a function of the thickness of the ferecrystal unit cell, since the electron-phonon coupling and the interlayer charge transfer are modulated by the number of layers (n). The control of the transition temperature by varying the m index instead in a [(SnSe)_1+δ]_m(NbSe₂) ferecrystal has also been observed.⁵⁴Fig. 2(b) and (c) show, respectively, the cross-sectional TEM images of a misfit layer compound⁵¹ and ferecrystal⁵³ superconducting superlattice.

To summarize this section, the composition of the unit cell in terms of the number of layers and crystalline phase of each material determines the coupling and charge transfer between layers, which are the factors that most influence the thermoelectric and electronic properties of this type of superlattices.

2.2 2D material layer-intercalated compound superlattices

In the previous section, it was discussed how the interlayer interactions between the layers that are part of a vertical stacking have a big influence on the cross-plane properties of the superlattice. Therefore, the coupling between layers for each system was adjusted by controlling the thickness, the doping and the crystallographic structure of the constituents. This peculiar interlayer spacing characteristic of van der Waals layered materials is found to have a considerable impact on the optical and electrical properties of the devices fabricated by or involved in intercalation methods. This section will review the works where ions or molecules were intercalated between the layers of a 2D material forming a different kind of superlattice.

A simultaneous enhancement in both the optical transmission and the electrical conduction through the phase change underwent by a 2D material after intercalation has been demonstrated in copper-intercalated bismuth-based chalcogenide layers.^55,56 The effect of Li intercalation on the charge density in different van der Waals heterostructures has been recently studied.⁵⁷ The tuning of the electrical and optical properties through intercalation has been also observed in ammonia ions-WS₂ host,⁵⁸ lithium ions-NbSe₂ host,⁵⁹ cetyl-trimethylammonium bromide (CTAB) in black phosphorus (BP),⁶⁰ and tetraethylbenzidine (EtDAB) ions in PbI₂.⁶¹ In a recent work, the coexistence of superconductivity and ferromagnetism originated from non-superconducting and non-ferromagnetic components has been achieved by the fabrication of a two-dimensional SnSe₂/Co(Cp)₂ superlattice, where Cp represents cyclopentadienyl molecules. A TEM cross-section of the superlattice is shown in Fig. 3(a) (left). The confinement effect that the Co(Cp)₂ molecules experience when they are sandwiched between the SnSe₂ layers weakens their coordination field, inducing the high spin ferromagnetic state (scheme in Fig. 3(a), right). The strong interlayer coupling between the Cp molecules and the SnSe₂ lattice induces a superconducting state through an unusual electron transfer.⁶²

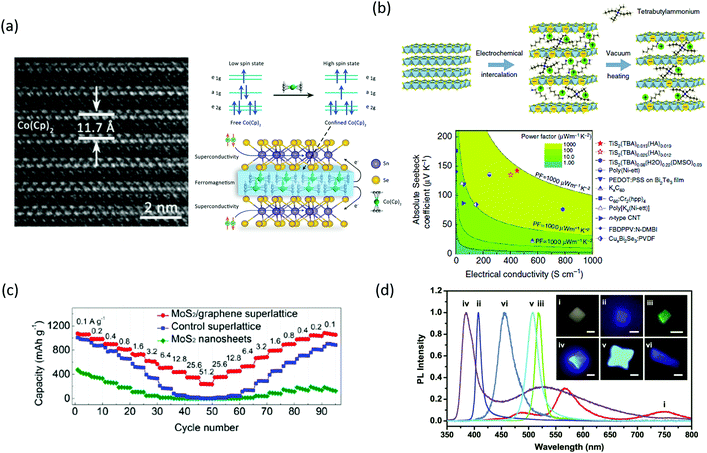Fig. 3 (a) Cross-sectional TEM image of the SnSe₂-Co(Cp)₂ superlattice (left). Scheme where the unit cell of the superlattice is shown, as well as the induced high spin state in the Co(Cp)₂ molecules when they are confined between the SnSe₂ layers (right). Reproduced with permission from ref. 51. (b) Scheme of one of the fabricated superlattices after electrochemical intercalation of hexylammonium/tetrabutylammonium molecules and vacuum heating (top). The absolute Seebeck coefficient represented as a function of the electrical conductivity shows that the intercalated TiS₂ compounds have a higher power factor compared to other thermoelectric materials (bottom). Reproduced with permission from ref. 52. (c) Rate capability as a function of cycling number of the 1T MoS₂/graphene superlattice is higher compared to control devices (1H MoS₂/graphene superlattice) and MoS₂ nanosheets. Reproduced with permission from ref. 57. (d) PL spectra of different 2D hybrid perovskites (corresponding to the crystals shown in the optical PL images of the inset). By optimizing the conditions of the same synthesis process, it is possible to achieve crystals with different wavelengths in the visible. Reproduced with permission from ref. 64.

In the previous section, we discussed how the interlayer disorder found in misfit layer compounds and ferecrystals could be controlled to optimize the carrier mobility and reduce the thermal conductivity to achieve high ZT for thermoelectric applications. Wan et al.^63–65 employed another approach to achieve a similar effect in TiS₂. The authors intercalated at the interface of TiS₂ thin layers organic cations such as hexylammonium ions (HA) and polar organic molecules such as dimethyl sulfoxide (DMSO). A scheme of the fabrication process is shown in Fig. 3(b) (top).⁶⁵ The reason behind was to engineer the dielectric constant between the two-dimensional TiS₂ layers to optimize the electrical mobility/thermal conductivity ratio. With this hybrid inorganic–organic superlattice structure, the authors obtained a thermal conductivity 7 times lower compared to that of TiS₂ single crystals.⁶⁴ A further improvement of this process led to the attainment of a power factor of 904 μW m⁻¹ K⁻², considerably higher compared to other thermoelectric materials, as shown in Fig. 3(b) (bottom).⁶⁵

There is a research effort devoted to optimize 2D material superlattices for energy storage applications.⁶⁶ In a smart design, MoS₂ monolayers were self-assembled by means of dopamine molecules adsorbed on their surface. After annealing, the dopamine layers sandwiched between the MoS₂ monolayers were thermally converted into nitrogen-doped graphene. This fabrication process results in a superlattice-like structure with good anode performance for lithium ion batteries. The fast charge–discharge rate and high cycling stability are attributed to the increase of reactive sites inherent to the new structure and an intimate interfacial coupling that enhances the electric and charge transfer.⁶⁷ In Sasaki's group, a superlattice based on metallic 1T-MoS₂/graphene monolayers has been fabricated by Li intercalation and solution-phase direct assembly. This superlattice was used as an anode for sodium ion batteries. It showed a larger capacity performance compared to the MoS₂ nanosheets and the 1H-MoS₂ monolayer/graphene monolayer superlattice (Fig. 3(c)) and a long-term stability up to 1000 cycles.⁶⁸ The same group has demonstrated the superior performance of metal oxide based anodes for lithium or sodium ion batteries when they are integrated in a van der Waals stacking superlattice. Two-dimensional metal oxides and hydroxides present optical properties and rich redox states that make them promising for energy storage applications. The authors fabricated a superlattice based on intercalated MnO₂ monolayers/graphene monolayers. The hybridization of the MnO₂/graphene monolayers resulted in enhanced conductivity, achieving faster charge transport, a larger specific capacity and long-term stability up to 5000 cycles.⁶⁹ In a third approach, the same authors fabricated a Ti_0.87O₂ monolayer/graphene monolayer superlattice as an anode for sodium ion batteries, where the titanium oxide layer was synthesized with Ti vacancies to increase the number of redox active sites and the graphene layer to enhance the conductivity.⁷⁰ When layered double hydroxide layers are inserted between MoS₂ monolayers, the strong interaction that takes place at the interface strengthens their electronic coupling, and thus, improves the electrical and charge transfer. As a result, the superlattice acts as a catalyst for overall water splitting.⁷¹

The achievement of improved performance or novel phenomena from a given two-dimensional material by tuning its dimensionality and/or intercalating organic molecules in the interlayer space is also followed by the hybrid organic–inorganic perovskite field. Efficient blue LEDs at room temperature were fabricated from two-dimensional (RNH₃)₂[CH₃NH₃PbX₃]_nPbX perovskites by (a) controlling the stacking number that gives rise to blue shift by quantum confinement and (b) designing dielectric quantum wells with organic host compounds to enhance the exciton binding energy and boost radiative recombination.⁷² The control of the layer thickness in Ruddlesden–Popper type of perovskites, with the general formula of (RNH₃)₂(CH₃NH₃)_n−1M_nX_3n+1, has been studied to change the bandgap for achieving photodetectors with tunable wavelength^73–75 and to tune the cross-plane acoustic phonon transport.⁷⁶ In Fig. 3(d) we have presented the tunability of the wavelength as a function of the composition of 2D perovskites fabricated with the same synthesis process.⁷⁵ The level of anisotropy as a function of the n inorganic layers in a 2D EA₂MA_n−1PbI_3n+1 perovskite, where EA = HOC₂H₄NH³⁺ and MA = CH₃NH³⁺, was studied. The two dimensional perovskite with n = 1 and layer-edge 0° device displayed a humidity sensitivity almost four orders of magnitude higher than that of the 3D homologous perovskite.⁷⁷

In this section, ions and molecules intercalated between the layers of the host 2D material were the elements employed to modulate the interlayer coupling and charge transfer to obtain superlattices with improved electronic, optical and thermoelectrical properties and to enhance the chemical reactivity, fundamental for energy-storage applications.

2.3 Moiré superlattices

The main approach to obtain moiré superlattices is the stacking of two 2D layered materials with a controlled rotation angle or lattice mismatch. These two materials can be equal, such as in the case of a twisted double-layer graphene⁷⁸ or the creation of a moiré superlattice from the rotation of the topmost layer of a Bi₂Te₃ quintuple layer.⁷⁹ Nevertheless, another common moiré superlattice is created by the stacking and twisting of two different materials, such as graphene on hexagonal boron nitride (h-BN),⁸⁰ or by van der Waals epitaxial growth of one of the materials over the other, such as Bi₂Se₃ on h-BN,⁸¹ GaSe monolayer on MoSe₂ monolayer,⁸² MoS₂ monolayer on WSe₂ monolayer⁸³ and SnS₂ monolayers on WSe₂ monolayers.⁸⁴ Recently, the creation of a third moiré superlattice with a larger potential period from the overlap of the bottom and top moiré superlattices in a h-BN/graphene/h-BN system was demonstrated.⁸⁵

The number of novel quantum phenomena observed experimentally in graphene/h-BN moiré superlattices is impressive and it is increasing fast. We refer the readers interested in more details about this topic to a recent review.⁸⁶ The periodic potential created by the lattice mismatch between graphene and h-BN gives rise to new Dirac points whose energy depends on the wavelength of the moiré potential.⁸⁷ Two dimensional electrons under the simultaneous application of a magnetic field and a periodic electrostatic potential display a fractal-like quantized energy spectrum called Hofstadter's butterfly.⁸⁸ In 2013, Hofstadter's butterfly was observed experimentally on graphene/h-BN lattices with small angle mismatches in the range of 4°–15° by three different groups.^89–91 A scheme of the device and the experimentally observed Hofstadter's butterfly spectra are shown in Fig. 4(a).⁸⁹ Later, one of these groups proved the coexistence of fractional quantum Hall effect states with integer states associated with Hofstadter's butterfly spectrum and the apparition of novel fractional Bloch quantum Hall effect states at high magnetic fields.⁹² With these results, the complete unit cell of the butterfly spectrum is covered. Another of these groups have studied further the novel Bloch states that lead to quantum oscillations, associated to Hofstadter's butterfly.^93,94 The commensurate stacking leading to topological bands and the incommensurate stacking leading to non-topological bands (due to the inhomogeneous potential landscape induced by the moiré pattern) can be achieved by controlling the twist angle between graphene and h-BN.^95,96 A gate-tunable Mott insulator was demonstrated by varying the bandgap of an h-BN/trilayer graphene/h-BN moiré superlattice with a vertical electric field.⁹⁷ Novel plasmonic modes arisen from the Dirac mini-bands found in the moiré superlattice were observed.⁹⁸ Electron tunnelling spectroscopy was used to measure the energy gaps formed at the first and second Dirac points of mono- and bilayer graphene/h-BN moiré superlattices as a function of twist angles and external electric and magnetic fields.⁹⁹

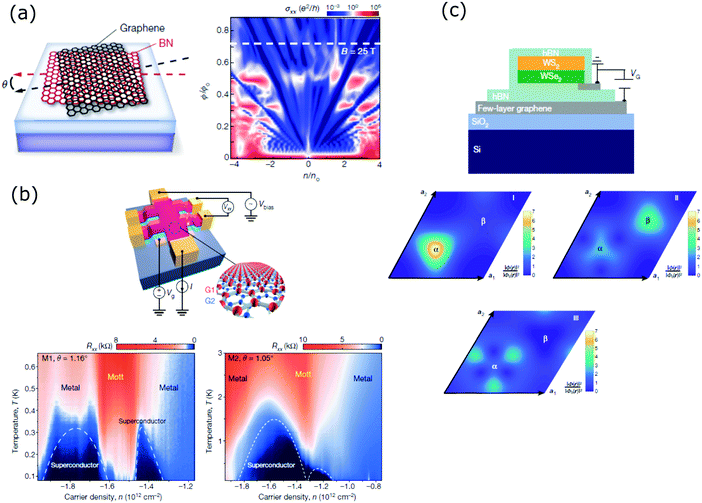Fig. 4 (a) Scheme of the twisted graphene and h-BN at an angle θ. The moiré wavelength can be designed as a function of θ (left). Hall conductivity σ_xx as a function of the normalized magnetic flux per unit cell and carrier density. A Hofstadter's butterfly with its characteristic fractal behaviour is displayed (right). Reproduced with permission from ref. 78. (b) Scheme of a twisted bilayer graphene fabricated as a 4-probe Hall bar device (top). 4-Probe resistance R_xx measured as a function of the temperature and carrier density for two different twist angles, 1.05° and 1.16°, very close to the ‘magic angle = 1.1°’. Both graphs show superconducting behaviour (bottom row) under the two angles, with variations in the superconducting domes. Reproduced with permission from ref. 90. (c) Scheme of the device, where the transition metal dichalcogenide monolayers have a twist angle close to zero (top). Real-space distribution of exciton centre-of-mass wavefunction. These maps show the apparition of three different moiré minibands (states I–III) in the strong-coupling regime (middle and bottom row). With permission from ref. 97.

Although it was predicted theoretically in 2011,¹⁰⁰ the experimental observation of unconventional superconductivity in two graphene layers twisted by a magic angle of about 1.1° in 2018, by Jarillo-Herrero's group, has shaken up the physics community. Fig. 4(b) shows the 4-probe resistance R_xx measured as a function of the carrier density and the temperature for two different devices. Both devices with the magic angles of 1.16° and 1.05°, respectively, display two superconducting domes, overlapped in the second case.¹⁰¹ This work has boosted the emergence of the twistronics field,^102,103 where all the rich electronic properties and range of magical angles in graphene twisted double-layers are being investigated.^104–106 On the other hand, the possibility to extend the study to other van der Waals layers twisted at small angles in order to produce novel collective excitation behaviours was soon realized. Different research groups have observed moiré interlayer excitons in MoSe₂/MoS₂,¹⁰⁷ WSe₂/WS₂¹⁰⁸ and MoSe₂/WSe₂¹⁰⁹ moiré superlattices. Jin et al. fabricated a fully h-BN encapsulated WSe₂/WS₂ heterostructure, with a measured twist angle of 0.5 ± 0.3° (Fig. 4(c), top). At the strong-coupling regime of a large moiré potential, three moiré exciton minibands appeared, represented in Fig. 4(c), since under this regime the moiré potential is stronger than the exciton kinetic energy.¹⁰⁸

The influence of the interlayer interface on the physical properties is common in all types of two-dimensional van der Waals superlattices. A scanning tunnelling microscopy tip was employed to apply pressure on a graphene/h-BN superlattice, controlling the interlayer distance between the layers. It was demonstrated that the degree of commensurate stacking and the in-plane strain of graphene can be controlled as a function of the interlayer distance, tuning the electronic properties.¹¹⁰ A laser induced shocking wave was used to eliminate wrinkles, bubbles and residues in the interlayer spaces of graphene/BN/graphene moiré superlattices. This produced a reduction of the interlayer distance between the graphene layers and the boron nitride and an enhancement in the interlayer electron coupling. As a consequence, an opening of a small bandgap was observed.¹¹¹ It has been predicted theoretically that by controlling the interlayer hybridization, a mosaic pattern with local topological insulator areas and normal insulator areas in moiré superlattices was formed by two massive Dirac materials.¹¹²

The results explained in this section show how an in-plane periodic potential can be introduced by stacking materials with a certain lattice mismatch or by twisting two 2D material layers under small angles. This method constitutes a novel approach to create superlattices with additional minibands, which display unconventional magnetic, superconducting, electronic and optical states.

2.4 Strain-engineered superlattices

Strain engineering is one of the most powerful strategies to modify the electronic and optical properties of 2D materials.^113–116 Strain is usually introduced unintentionally in many growth, mechanical stacking and device fabrication steps and its influence on the properties of the final superlattice should be addressed. But controlling the strain constitutes another route to tune the properties in superlattices and even to build up novel systems where periodic variation of strain leads to the fabrication of superlattices.

In Section 2.1, we have described the interfacial phase-change memory materials based on Sb₂Te₃–GeTe vertical vdW superlattices. Zhou et al. improved the switching speed and lowered the energy consumption of their device by optimizing the synthesis of Sb₂Te₁–GeTe superlattices. The GeTe layers were grown on the Sb₂Te₁ layers subjected to a biaxial strain.¹¹⁷ Another group tuned the level of induced biaxial strain on the GeTe layers of a Sb₂Te₃–GeTe 2D superlattice by varying the thickness of the Sb₂Te₃ layer.¹¹⁸ Almost at the same time, three different groups^119–121 correlated the unexpected opening of gaps in graphene/h-BN moiré superlattices with the existence of corrugations or in-plane strain on the graphene and proposed theoretical models to explain this phenomenon. San-Jose et al.¹²⁰ claimed that a displacement and an in-plane strain are produced in graphene due to the adhesion forces between the graphene and h-BN layers. They used known elastic constants for graphene and first-principles simulations to characterize the level of distortion as a function of the twist angle. The strain/distortion level represented as the local expansion (Tr(u)/2 in Fig. 5(a), top) was calculated for angles of 0°, 1.5° and 4° (Fig. 5(a), top). They calculated the generated pseudomagnetic field for the same twist angles (Fig. 5(a), bottom). A theoretical study showed that the strain along the three principal directions of a graphene layer can induce strong gauge fields that behave as pseudo-magnetic fields, observing a new quantum Hall effect.¹²² Lateral superlattices of alternating graphene/h-BN layers were studied theoretically to investigate the mismatch strain-relief mechanisms at the interface, which happened by misfit dislocations or by the formation of a periodic rippling as an out-of-plane relaxation.¹²³ The motivation behind this work was to point out the importance of controlling the experimental conditions to avoid the mismatch strain and obtain coherent graphene/h-BN interfaces. The strain induced by the gold contacts on a graphene/h-BN moiré superlattice and its influence on the electrical properties have been studied as well.¹²⁴

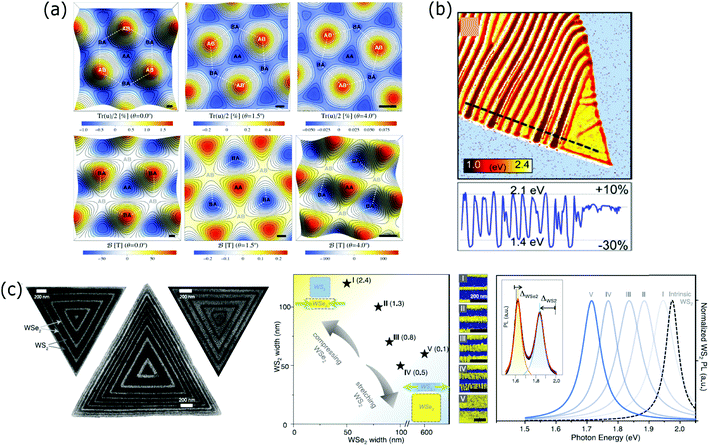Fig. 5 (a) Relative local expansion Tru/2 simulated in real space for twist angles of 0°, 1.5° and 4°. These mappings represent the level of straining as a function of the rotation angle (top). Pseudomagnetic field distribution simulated in real space for the same twist angles of 0°, 1.5° and 4°. These mappings represent the fields that originate as a result of the level of straining (bottom). Reproduced with permission from ref. 109. (b) Iso-absorption map representing the energy at which the squared absorption coefficient is equivalent to 7.5 × 10⁻¹¹ cm⁻² at each point (top). A cross section along the dashed black line is shown at the bottom. The images show the existence of spatially variable absorption spectra following the periodic compressive and tensile strain regions in the BP ripples. Reproduced with permission from ref. 114. (c) SEM images of three different WS₂/WSe₂ superlattices fabricated from coherent epitaxial growth (left). Graph with the aspect ratios (values in parentheses) of the WS₂/WSe₂ widths at which the I to V superlattices were obtained and false-colour SEM images of the I–V superlattices (middle). Normalized PL spectra of the I–V superlattices together with the peak corresponding to the intrinsic WS₂ to show the shift in wavelength (right). The inset spectrum of a typical WS₂/WSe₂ superlattice is represented to illustrate the relative WS₂ peak red-shift and the relative WSe₂ peak blue-shift. Reproduced with permission from ref. 115.

Tuning the bandgap of semiconducting 2D materials is one of the main aims of strain engineering, relevant for optoelectronic applications. The formation of periodic ripples on a black phosphorus thin layer gave rise to an absorption spectrum with periodic absorption edge shifts of +10% and −30%, corresponding to the regions under tensile and compressive strains.¹²⁵ An iso-absorption map shown in Fig. 5(b) illustrates the spatially varying optical properties induced by the periodic ripples of the black phosphorus flake. Coherent, full-matching lattice constants in-plane WS₂/WSe₂ superlattices were fabricated by metal–organic chemical vapor deposition. SEM images of three different superlattices are shown in Fig. 5(c) (left). The lattice coherence has been achieved by tensile (compressive) strain in the WS₂ (WSe₂) components. The ratio of their widths allows controlling the degree of strain, producing different types of superlattices (labelled as I to V within the panel) (Fig. 5(c), middle). Each type of superlattice (I to V) presents a red- (blue-) shifted peak in the photoluminescence spectra with respect to the intrinsic WS₂ (WSe₂). The spectrum is shown in Fig. 5(c) (right) and demonstrates the potential to use this approach for tunable optoelectronic devices.¹²⁶ The misfit dislocations formed at the interface of a lateral WSe₂/WS₂ heterostructure as a result of the lattice mismatch between both layers were used as templates to grow WS₂ sub-2 nm quantum wells on a WSe₂ matrix superlattice by chemical vapour deposition. The strain field surrounding the misfit dislocations was found to induce dislocation climb by the preferential growth of the quantum wells.¹²⁷

Rigorously, strain is the mechanism that is common in almost all types of superlattices described in this Feature article through the lattice mismatch or the stress induced on the 2D material layers when they are stacked together or placed in a patterned topography. For this reason, a deep study and understanding of its influence on the fabrication of superlattices in particular, and any other device in general, will be fundamental for the advance of the 2D materials field.

2.5 Lithographic-engineered superlattices

This section includes those works where the periodicity of the superlattice was created by either transferring a 2D material onto a substrate with an ordered array of structures that served as templates to tailor its electronic and optical properties or by patterning selectively a 2D material layer by a lithographic method.

The top panel of Fig. 6(a) shows a schematic of a MoS₂ monolayer transferred onto an array of periodic SiO₂ nanocones, which are assembled by nanosphere lithography. At the apex of the nanocones, the more stretched areas of MoS₂ present a high tensile strain, which results in a periodic decrease in its optical bandgap. Therefore, a large area artificial-atom crystal is produced. Raman and photoluminescence measurements showed that the crystal presented a large exciton binding energy. Fig. 6(a) (bottom left) shows a scanning PL map of the artificial crystal. Under illumination with wavelength larger than the bandgap of MoS₂, excitons are created in MoS₂. These excitons drift towards the nanocone tips and then are emitted with a larger wavelength. A scheme of the process is shown in Fig. 6(a) (bottom right).¹²⁸ Another group employed an alternative approach to fabricate artificial superlattices based on a MoS₂ monolayer. They generated a periodic array of quantum dots inducing local phase change from 2H (semiconducting) to 1T (metallic) by focused electron beam exposure. By controlling the size and the pitch of the quantum dots, the tuning of the bandgap from 1.81 to 1.42 eV was demonstrated.¹²⁹ An artificial superlattice was achieved by transferring a graphene layer onto a self-assembled array of silicon oxide nanoparticles. The quasi-periodic strain produced on graphene gave rise to minibands with broad density of states. The authors claimed that this result constituted a cheap and simple process to fabricate superlattices for optical modulators or infrared sensors.¹³⁰ In another work, a graphene layer was transferred onto an array of gold nanoislands. Thermal annealing creates a hybrid graphene/gold superstructure where the stretching of graphene and the phase change in gold gave rise to unusually large moiré periodicities.¹³¹

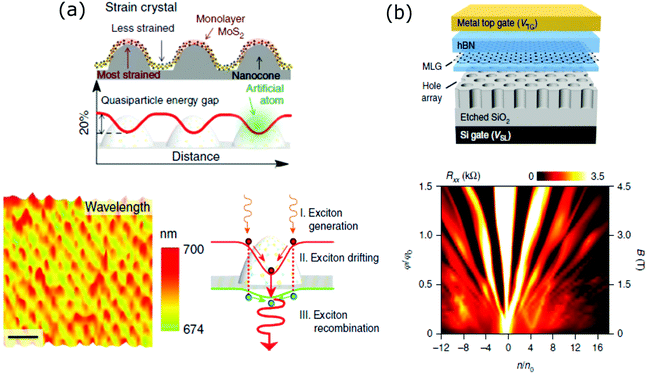Fig. 6 (a) Scheme of the artificial-atom crystal by transferring of the MoS₂ monolayer on an array of periodic SiO₂ nanocones. The energy bandgap reduction is inverse of the strain level (top). Scanning PL spectroscopy mapping of the artificial crystal (bottom left). Scheme of the process that the excitons undergo once they are induced on the artificial crystal under light exposure (bottom right). Reproduced with permission from ref. 117. (b) Scheme of a final device consisting of a fully encapsulated graphene structure transferred onto a patterned dielectric superlattice (top). Device R_xx resistance measured as a function of normalized density and magnetic field. A Hofstadter butterfly behaviour is achieved. Conditions: V_superlattice = 50 V, T = 250 mK, application of a triangular periodic potential (bottom). Reproduced with permission from ref. 122.

The previous section showed the results where moiré patterning was employed to tune the bandgap structure of graphene. A second route to achieve this is by nanostructuring the material by lithographic methods. In a recent work, an array of triangular shaped holes with a pitch of 35 nm and minimum feature sizes of 12–15 nm was defined on a h-BN/graphene/h-BN heterostructure by electron beam lithography. The small size and the high density of the holes were chosen to manipulate the electronic and magnetic quantum transport behaviour.¹³² A third route to engineer the electronic properties of graphene is by applying external electric fields rather than modifying the material itself. A fully encapsulated h-BN/graphene/h-BN heterostructure was transferred onto a 300 nm SiO₂ substrate with an array of periodic nanoholes defined by electron beam lithography. A scheme of the device is shown in Fig. 6(b), top. This patterned dielectric layer was the component that induced a superlattice structure on graphene, by introducing periodic potentials with triangular or square unit cells. As a result, Dirac cones and Hofstadter butterfly behaviours were replicated from non-moiré generated superlattices. Fig. 6(b) (bottom) shows a Hofstadter's butterfly spectrum achieved at 4.5 T, while the observation of the Hofstadter spectrum from moiré superlattices requires magnetic fields higher than 20 T up to now.¹³³

Lithography is ubiquitous in the fabrication of devices. However, in the case of 2D material based superlattices, the results from the examples shown in this section can be obtained by using one of the methods described in the previous sections. This poses the question whether the lithographic-engineered approach is well-suited to produce optimal van der Waals based superlattices in comparison with the other strategies, since the mixed dimensionality of a 2D material flake and the 3D pattern substrate can introduce an additional complexity to the interlayer interaction and expensive and complex techniques such as electron and focused ion beam are required to define high-resolution periodic potentials on a 2D material surface.

3 Conclusion and outlook

2D materials and their van der Waals interlayer interaction display physical and chemical properties unobserved in their bulk counterparts. This unique trait has opened the way to produce devices with novel architectures, among which the fabrication of van der Waals 2D material superlattices has been explored. Our aim in the present Feature article was to underscore the huge potential and relevance of this type of structures, which comprise a very young field yet. The first prototypes have shown improved thermoelectric, optoelectronic, phase-change memory and energy storage performances, compared to the devices fabricated with established methods. These achievements constitute an invitation to explore the two-dimensional material based superlattices for solving environmental and energy consumption related issues. Particularly, they could have a great impact on the thermoelectrical and Li-/Na-storage applications. At the fundamental level, the moiré superlattices have displayed novel electronic, excitonic, superconductive, and magnetic states. The field of twistronics has just started and a plethora of new physical phenomena is expected in the future. Strain is present in almost all types of superlattices, both introduced unintentionally or as a variable to modulate their properties. Therefore, a rigorous study of the influence of strain or strain engineering on the final properties of the structures will be fundamental for the controlled fabrication of high-quality superlattices. The superlattices based on van der Waals 2D materials have shown huge versatility. As an example, the bandgap can be modulated by the composition of the superlattice unit cell, controlling the interlayer interaction, intercalating ions or molecules at the interlayer, moiré patterning, strain engineering, and combining 2D materials with conventional lithographic approaches. This illustrates the potential to design and devise superlattices. For the same reason, many research groups from different chemical and physical backgrounds can have access to their fabrication. Finally, the improvement and expansion of the robotic assembly approach will be crucial for the viability of 2D material based superlattices at both the academic and industrial level. At the academic level, automation would allow the researchers to save time and increase the success yield in the fabrication of complex superlattices, in order to focus on the study and engineering of their properties. The robotic assembly has room to introduce more variables such as the twist angle, the doping level or the cleaning of the flakes, which will result in the production of high-quality superlattices. At the industrial level, the remaining challenge is the implementation of large-scale manufacturing of these superlattices.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This project has received funding from the European Research Council (ERC) under European Union's Horizon 2020 research and innovation programme (grant agreement no 755655, ERC-StG 2017 project 2D-TOPSENSE). R. F. acknowledges the support from the Spanish Ministry of Economy, Industry and Competitiveness through a Juan de la Cierva-formación fellowship 2017 FJCI-2017-32919. We acknowledge support of the publication fee by the CSIC Open Access Publication Support Initiative through its Unit of Information Resources for Research (URICI).

References

1. L. Esaki and R. Tsu, IBM J. Res. Dev., 1970, 14, 61–65.
2. L. Esaki and L. L. Chang, Phys. Rev. Lett., 1974, 33, 495–498.
3. G. C. Osbourn, IEEE J. Quantum Electron., 1986, 22, 1677–1681.
4. H. T. Grahn, Semiconductor superlattices: growth and electronic properties, World Scientific, 1995.
5. R. Tsu, Superlattice to nanoelectronics, Elsevier, 2010.
6. E. E. Mendez and K. von Klitzing, Physics and applications of quantum wells and superlattices, Springer Science & Business Media, 2012, vol. 170.
7. C. M. Lieber, Nano Lett., 2002, 2, 81–82.
8. M. Hu and D. Poulikakos, Nano Lett., 2012, 12, 5487–5494.
9. M. Hocevar, G. Immink, M. Verheijen, N. Akopian, V. Zwiller, L. Kouwenhoven and E. Bakkers, Nat. Commun., 2012, 3, 1–6.
10. J. K. Hyun, S. Zhang and L. J. Lauhon, Annu. Rev. Mater. Res., 2013, 43, 451–479.
11. M. Zhao, Y. Wang, Q. Ma, Y. Huang, X. Zhang, J. Ping, Z. Zhang, Q. Lu, Y. Yu, H. Xu, Y. Zhao and H. Zhang, Adv. Mater., 2015, 27, 7372–7378.
12. Y. Dou, L. Zhang, J. Xu, C. T. He, X. Xu, Z. Sun, T. Liao, B. Nagy, P. Liu and S. X. Dou, ACS Nano, 2018, 12, 1878–1886.
13. S. Gu, S. Wu, L. Cao, M. Li, N. Qin, J. Zhu, Z. Wang, Y. Li, Z. Li, J. Chen and Z. Lu, J. Am. Chem. Soc., 2019, 141, 9623–9628.
14. S. Wang, Q. Wang, P. Shao, Y. Han, X. Gao, L. Ma, S. Yuan, X. Ma, J. Zhou, X. Feng and B. Wang, J. Am. Chem. Soc., 2017, 139, 4258–4261.
15. A. J. Molina-Mendoza, E. Giovanelli, W. S. Paz, M. A. Niño, J. O. Island, C. Evangeli, L. Aballe, M. Foerster, H. S. J. Van Der Zant and G. Rubio-Bollinger, et al. , Nat. Commun., 2017, 8, 14409.
16. M. Velický, P. S. Toth, A. M. Rakowski, A. P. Rooney, A. Kozikov, C. R. Woods, A. Mishchenko, L. Fumagalli, J. Yin, V. Zólyomi, T. Georgiou, S. J. Haigh, K. S. Novoselov and R. A. W. Dryfe, Nat. Commun., 2017, 8, 14410.
17. K. Ray, A. E. Yore, T. Mou, S. Jha, K. K. H. Smithe, B. Wang, E. Pop and A. K. M. Newaz, ACS Nano, 2017, 11(6), 6024–6030.
18. G. Prando, Nat. Nanotechnol., 2017, 12, 191.
19. R. Gusmão, Z. Sofer, J. Luxa and M. Pumera, J. Mater. Chem. A, 2018, 6(34), 16590–16599.
20. Y. Niu, J. Villalva, R. Frisenda, G. Sanchez-Santolino, L. Ruiz-González, E. M. Pérez, M. García-Hernández, E. Burzurí and A. Castellanos-Gomez, 2D Mater., 2019, 6, 035023.
21. G. H. Moh, Mineral. Petrol., 1987, 36, 191–204.
22. K. Kang, K.-H. Lee, Y. Han, H. Gao, S. Xie, D. A. Muller and J. Park, Nature, 2017, 550, 229.
23. S. Masubuchi, M. Morimoto, S. Morikawa, M. Onodera, Y. Asakawa, K. Watanabe, T. Taniguchi and T. Machida, Nat. Commun., 2018, 9, 1413.
24. S. Vishwanath, X. Liu, S. Rouvimov, L. Basile, N. Lu, A. Azcatl, K. Magno, R. M. Wallace, M. Kim and J.-C. Idrobo, et al. , J. Mater. Res., 2016, 31, 900–910.
25. A. Koma, Thin Solid Films, 1992, 216, 72–76.
26. M. Lin, D. Wu, Y. Zhou, W. Huang, W. Jiang, W. Zheng, S. Zhao, C. Jin, Y. Guo and H. Peng, et al. , J. Am. Chem. Soc., 2013, 135, 13274–13277.
27. Y. Zhao, H. Liu, X. Guo, Y. Jiang, Y. Sun, H. Wang, Y. Wang, H.-D. Li, M.-H. Xie and X.-C. Xie, et al. , Nano Lett., 2014, 14, 5244–5249.
28. X.-B. Li, N.-K. Chen, X.-P. Wang and H.-B. Sun, Adv. Funct. Mater., 2018, 28, 1803380.
29. J. Momand, R. Wang, J. E. Boschker, M. A. Verheijen, R. Calarco and B. J. Kooi, Nanoscale, 2015, 7, 19136–19143.
30. S. Cecchi, E. Zallo, J. Momand, R. Wang, B. J. Kooi, M. A. Verheijen and R. Calarco, APL Mater., 2017, 5, 26107.
31. A. V. Kolobov, P. Fons, Y. Saito and J. Tominaga, ACS Omega, 2017, 2, 6223–6232.
32. J. Tominaga, Y. Saito, K. Mitrofanov, N. Inoue, P. Fons, A. V. Kolobov, H. Nakamura and N. Miyata, Adv. Funct. Mater., 2017, 27, 1702243.
33. J. K. Behera, X. Zhou, A. Ranjan and R. E. Simpson, ACS Appl. Mater. Interfaces, 2018, 10, 15040–15050.
34. R. Mondal, Y. Aihara, Y. Saito, P. Fons, A. V. Kolobov, J. Tominaga and M. Hase, ACS Appl. Mater. Interfaces, 2018, 10, 26781–26786.
35. M. Falmbigl, M. B. Alemayehu, D. R. Merrill, M. Beekman and D. C. Johnson, Cryst. Res. Technol., 2015, 50, 464–472.
36. D. Merrill, D. Moore, S. Bauers, M. Falmbigl and D. Johnson, Materials, 2015, 8, 2000–2029.
37. M. Beekman, C. L. Heideman and D. C. Johnson, Semicond. Sci. Technol., 2014, 29, 64012.
38. R. D. Westover, J. Ditto, M. Falmbigl, Z. L. Hay and D. C. Johnson, Chem. Mater., 2015, 27, 6411–6417.
39. R. Atkins, J. Wilson, P. Zschack, C. Grosse, W. Neumann and D. C. Johnson, Chem. Mater., 2012, 24, 4594–4599.
40. G. Mitchson, E. Hadland, F. Göhler, M. Wanke, M. Esters, J. Ditto, E. Bigwood, K. Ta, R. G. Hennig and T. Seyller, et al. , ACS Nano, 2016, 10, 9489–9499.
41. D. M. Hamann, A. C. Lygo, M. Esters, D. R. Merrill, J. Ditto, D. R. Sutherland, S. R. Bauers and D. C. Johnson, ACS Nano, 2018, 12, 1285–1295.
42. M. B. Alemayehu, K. Ta, M. Falmbigl and D. C. Johnson, Nanoscale, 2015, 7, 7378–7385.
43. F. Göhler, G. Mitchson, M. B. Alemayehu, F. Speck, M. Wanke, D. C. Johnson and T. Seyller, J. Phys.: Condens. Matter, 2018, 30, 55001.
44. M. Falmbigl, A. Fiedler, R. E. Atkins, S. F. Fischer and D. C. Johnson, Nano Lett., 2015, 15, 943–948.
45. D. R. Merrill, D. R. Sutherland, J. Ditto, S. R. Bauers, M. Falmbigl, D. L. Medlin and D. C. Johnson, Chem. Mater., 2015, 27, 4066–4072.
46. S. R. Wood, D. R. Merrill, G. Mitchson, A. C. Lygo, S. R. Bauers, D. M. Hamann, D. R. Sutherland, J. Ditto and D. C. Johnson, Chem. Mater., 2016, 29, 773–779.
47. C. Yin, Q. Hu, G. Wang, T. Huang, X. Zhou, X. Zhang, Y. Dou, B. Kang, J. Tang and N. Liu, et al. , Appl. Phys. Lett., 2017, 110, 43507.
48. P. Jood, M. Ohta, H. Nishiate, A. Yamamoto, O. I. Lebedev, D. Berthebaud, K. Suekuni and M. Kunii, Chem. Mater., 2014, 26, 2684–2692.
49. R. Guo, Y.-D. Jho and A. J. Minnich, Nanoscale, 2018, 10, 14432–14440.
50. Z. Li, S. R. Bauers, N. Poudel, D. Hamann, X. Wang, D. S. Choi, K. Esfarjani, L. Shi, D. C. Johnson and S. B. Cronin, Nano Lett., 2017, 17, 1978–1986.
51. H. Bai, X. Yang, Y. Liu, M. Zhang, M. Wang, Y. Li, J. Ma, Q. Tao, Y. Xie and G.-H. Cao, et al. , J. Phys.: Condens. Matter, 2018, 30, 355701.
52. R. Sankar, G. Peramaiyan, I. Panneer Muthuselvam, C.-Y. Wen, X. Xu and F. C. Chou, Chem. Mater., 2018, 30, 1373–1378.
53. C. Grosse, M. B. Alemayehu, M. Falmbigl, A. Mogilatenko, O. Chiatti, D. C. Johnson and S. F. Fischer, Sci. Rep., 2016, 6, 33457.
54. M. Trahms, C. Grosse, M. B. Alemayehu, O. K. Hite, O. Chiatti, A. Mogilatenko, D. C. Johnson and S. F. Fischer, Supercond. Sci. Technol., 2018, 31, 65006.
55. J. Yao, K. J. Koski, W. Luo, J. J. Cha, L. Hu, D. Kong, V. K. Narasimhan, K. Huo and Y. Cui, Nat. Commun., 2014, 5, 5670.
56. Y. Guo, J. Zhou, Y. Liu, X. Zhou, F. Yao, C. Tan, J. Wu, L. Lin, K. Liu and Z. Liu, et al. , Adv. Mater., 2017, 29, 1703424.
57. D. K. Bediako, M. Rezaee, H. Yoo, D. T. Larson, S. Y. F. Zhao, T. Taniguchi, K. Watanabe, T. L. Brower-Thomas, E. Kaxiras and P. Kim, Nature, 2018, 558, 425.
58. Q. Liu, X. Li, Z. Xiao, Y. Zhou, H. Chen, A. Khalil, T. Xiang, J. Xu, W. Chu and X. Wu, et al. , Adv. Mater., 2015, 27, 4837–4844.
59. E. Hitz, J. Wan, A. Patel, Y. Xu, L. Meshi, J. Dai, Y. Chen, A. Lu, A. V. Davydov and L. Hu, ACS Appl. Mater. Interfaces, 2016, 8, 11390–11395.
60. C. Wang, Q. He, U. Halim, Y. Liu, E. Zhu, Z. Lin, H. Xiao, X. Duan, Z. Feng and R. Cheng, et al. , Nature, 2018, 555, 231.
61. G. E. Wang, G. Xu, N. Zhang, M. S. Yao, M. S. Wang and G. C. Guo, Angew. Chem., 2019, 131(9), 2718–2721.
62. Z. Li, Y. Zhao, K. Mu, H. Shan, Y. Guo, J. Wu, Y. Su, Q. Wu, Z. Sun and A. Zhao, et al. , J. Am. Chem. Soc., 2017, 139, 16398–16404.
63. C. Wan, Y. Kodama, M. Kondo, R. Sasai, X. Qian, X. Gu, K. Koga, K. Yabuki, R. Yang and K. Koumoto, Nano Lett., 2015, 15, 6302–6308.
64. C. Wan, X. Gu, F. Dang, T. Itoh, Y. Wang, H. Sasaki, M. Kondo, K. Koga, K. Yabuki and G. J. Snyder, et al. , Nat. Mater., 2015, 14, 622.
65. C. Wan, R. Tian, M. Kondou, R. Yang, P. Zong and K. Koumoto, Nat. Commun., 2017, 8, 1024.
66. J. Xu, J. Zhang, W. Zhang and C.-S. Lee, Adv. Energy Mater., 2017, 7, 1700571.
67. C. Zhao, X. Wang, J. Kong, J. M. Ang, P. S. Lee, Z. Liu and X. Lu, ACS Appl. Mater. Interfaces, 2016, 8, 2372–2379.
68. P. Xiong, R. Ma, N. Sakai, L. Nurdiwijayanto and T. Sasaki, ACS Energy Lett., 2018, 3, 997–1005.
69. P. Xiong, R. Ma, N. Sakai and T. Sasaki, ACS Nano, 2018, 12, 1768–1777.
70. P. Xiong, X. Zhang, F. Zhang, D. Yi, J. Zhang, B. Sun, H. Tian, D. Shanmukaraj, T. Rojo and M. Armand, et al. , ACS Nano, 2018, 12, 12337–12346.
71. M. S. Islam, M. Kim, X. Jin, S. M. Oh, N.-S. Lee, H. Kim and S.-J. Hwang, ACS Energy Lett., 2018, 3, 952–960.
72. S. Kumar, J. Jagielski, S. Yakunin, P. Rice, Y.-C. Chiu, M. Wang, G. Nedelcu, Y. Kim, S. Lin and E. J. G. Santos, et al. , ACS Nano, 2016, 10, 9720–9729.
73. J. Zhou, Y. Chu and J. Huang, ACS Appl. Mater. Interfaces, 2016, 8, 25660–25666.
74. J.-C. Blancon, H. Tsai, W. Nie, C. C. Stoumpos, L. Pedesseau, C. Katan, M. Kepenekian, C. M. M. Soe, K. Appavoo and M. Y. Sfeir, et al. , Science, 2017, 355, 1288–1292.
75. L. Dou, A. B. Wong, Y. Yu, M. Lai, N. Kornienko, S. W. Eaton, A. Fu, C. G. Bischak, J. Ma and T. Ding, et al. , Science, 2015, 349, 1518–1521.
76. P. Guo, C. C. Stoumpos, L. Mao, S. Sadasivam, J. B. Ketterson, P. Darancet, M. G. Kanatzidis and R. D. Schaller, Nat. Commun., 2018, 9, 2019.
77. B. Cheng, T.-Y. Li, P.-C. Wei, J. Yin, K.-T. Ho, J. R. D. Retamal, O. F. Mohammed and J.-H. He, Nat. Commun., 2018, 9, 5196.
78. H. Schmidt, J. C. Rode, D. Smirnov and R. J. Haug, Nat. Commun., 2014, 5, 5742.
79. K. Schouteden, Z. Li, T. Chen, F. Song, B. Partoens, C. Van Haesendonck and K. Park, Sci. Rep., 2016, 6, 20278.
80. D. Wang, G. Chen, C. Li, M. Cheng, W. Yang, S. Wu, G. Xie, J. Zhang, J. Zhao and X. Lu, et al. , Phys. Rev. Lett., 2016, 116, 126101.
81. S. Xu, Y. Han, X. Chen, Z. Wu, L. Wang, T. Han, W. Ye, H. Lu, G. Long and Y. Wu, et al. , Nano Lett., 2015, 15, 2645–2651.
82. X. Li, M.-W. Lin, J. Lin, B. Huang, A. A. Puretzky, C. Ma, K. Wang, W. Zhou, S. T. Pantelides and M. Chi, et al. , Sci. Adv., 2016, 2, e1501882.
83. C. Zhang, C.-P. Chuu, X. Ren, M.-Y. Li, L.-J. Li, C. Jin, M.-Y. Chou and C.-K. Shih, Sci. Adv., 2017, 3, e1601459.
84. T. Yang, B. Zheng, Z. Wang, T. Xu, C. Pan, J. Zou, X. Zhang, Z. Qi, H. Liu and Y. Feng, et al. , Nat. Commun., 2017, 8, 1906.
85. L. Wang, S. Zihlmann, M.-H. Liu, P. Makk, K. Watanabe, T. Taniguchi, A. Baumgartner and C. Schönenberger, Nano Lett., 2019, 19(4), 2371–2376.
86. M. Yankowitz, Q. Ma, P. Jarillo-Herrero and B. J. LeRoy, Nat. Rev. Phys., 2019, 1.
87. M. Yankowitz, J. Xue, D. Cormode, J. D. Sanchez-Yamagishi, K. Watanabe, T. Taniguchi, P. Jarillo-Herrero, P. Jacquod and B. J. LeRoy, Nat. Phys., 2012, 8, 382.
88. D. R. Hofstadter, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 14, 2239.
89. C. R. Dean, L. Wang, P. Maher, C. Forsythe, F. Ghahari, Y. Gao, J. Katoch, M. Ishigami, P. Moon and M. Koshino, et al. , Nature, 2013, 497, 598.
90. B. Hunt, J. D. Sanchez-Yamagishi, A. F. Young, M. Yankowitz, B. J. LeRoy, K. Watanabe, T. Taniguchi, P. Moon, M. Koshino and P. Jarillo-Herrero, et al. , Science, 2013, 340, 1427–1430.
91. L. A. Ponomarenko, R. V. Gorbachev, G. L. Yu, D. C. Elias, R. Jalil, A. A. Patel, A. Mishchenko, A. S. Mayorov, C. R. Woods and J. R. Wallbank, et al. , Nature, 2013, 497, 594.
92. L. Wang, Y. Gao, B. Wen, Z. Han, T. Taniguchi, K. Watanabe, M. Koshino, J. Hone and C. R. Dean, Science, 2015, 350, 1231–1234.
93. R. K. Kumar, X. Chen, G. H. Auton, A. Mishchenko, D. A. Bandurin, S. V. Morozov, Y. Cao, E. Khestanova, M. Ben Shalom and A. V. Kretinin, et al. , Science, 2017, 357, 181–184.
94. R. K. Kumar, A. Mishchenko, X. Chen, S. Pezzini, G. H. Auton, L. A. Ponomarenko, U. Zeitler, L. Eaves, V. I. Fal’ko and A. K. Geim, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5135–5139.
95. C. R. Woods, L. Britnell, A. Eckmann, R. S. Ma, J. C. Lu, H. M. Guo, X. Lin, G. L. Yu, Y. Cao and R. V. Gorbachev, et al. , Nat. Phys., 2014, 10, 451.
96. J. C. W. Song, P. Samutpraphoot and L. S. Levitov, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 10879–10883.
97. G. Chen, L. Jiang, S. Wu, B. Lyu, H. Li, B. L. Chittari, K. Watanabe, T. Taniguchi, Z. Shi and J. Jung, et al. , Nat. Phys., 2019, 1.
98. G. X. Ni, H. Wang, J. S. Wu, Z. Fei, M. D. Goldflam, F. Keilmann, B. Özyilmaz, A. H. C. Neto, X. M. Xie and M. M. Fogler, et al. , Nat. Mater., 2015, 14, 1217.
99. H. Kim, N. Leconte, B. L. Chittari, K. Watanabe, T. Taniguchi, A. H. MacDonald, J. Jung and S. Jung, Nano Lett., 2018, 18, 7732–7741.
100. R. Bistritzer and A. H. MacDonald, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 12233–12237.
101. Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras and P. Jarillo-Herrero, Nature, 2018, 556, 43.
102. J. C. W. Song and N. M. Gabor, Nat. Nanotechnol., 2018, 13, 986.
103. D. H. Freedman, Quanta Mag., 2019, https://www.quantamagazine.org/how-twisted-graphene-became-the-big-thing-in-physics-20190430/.
104. X. Lu, P. Stepanov, W. Yang, M. Xie, M. A. Aamir, I. Das, C. Urgell, K. Watanabe, T. Taniguchi and G. Zhang, et al., arXiv Prepr. arXiv1903.06513.
105. S. S. Sunku, G. Ni, B.-Y. Jiang, H. Yoo, A. Sternbach, A. S. McLeod, T. Stauber, L. Xiong, T. Taniguchi and K. Watanabe, et al. , Science, 2018, 362, 1153–1156.
106. H. Yoo, R. Engelke, S. Carr, S. Fang, K. Zhang, P. Cazeaux, S. H. Sung, R. Hovden, A. W. Tsen, T. Taniguchi, K. Watanabe, G. C. Yi, M. Kim, M. Luskin, E. B. Tadmor, E. Kaxiras and P. Kim, Nat. Mater., 2019, 18, 448–453.
107. N. Zhang, A. Surrente, M. Baranowski, D. K. Maude, P. Gant, A. Castellanos-Gomez and P. Plochocka, Nano Lett., 2018, 18, 7651–7657.
108. C. Jin, E. C. Regan, A. Yan, M. Iqbal Bakti Utama, D. Wang, S. Zhao, Y. Qin, S. Yang, Z. Zheng, S. Shi, K. Watanabe, T. Taniguchi, S. Tongay, A. Zettl and F. Wang, Nature, 2019, 567, 76–80.
109. K. Tran, G. Moody, F. Wu, X. Lu, J. Choi, K. Kim, A. Rai, D. A. Sanchez, J. Quan and A. Singh, et al. , Nature, 2019, 1.
110. M. Yankowitz, K. Watanabe, T. Taniguchi, P. San-Jose and B. J. LeRoy, Nat. Commun., 2016, 7, 13168.
111. P. Kumar, J. Liu, M. Motlag, L. Tong, Y. Hu, X. Huang, A. Bandopadhyay, S. K. Pati, L. Ye and J. Irudayaraj, et al. , Nano Lett., 2018, 19, 283–291.
112. Q. Tong, H. Yu, Q. Zhu, Y. Wang, X. Xu and W. Yao, Nat. Phys., 2017, 13, 356.
113. R. Roldán, A. Castellanos-Gomez, E. Cappelluti and F. Guinea, J. Phys.: Condens. Matter, 2015, 27, 313201.
114. B. Amorim, A. Cortijo, F. de Juan, A. G. Grushin, F. Guinea, A. Gutiérrez-Rubio, H. Ochoa, V. Parente, R. Roldán, P. San-Jose, J. Schiefele, M. Sturla and M. A. H. Vozmediano, Phys. Rep., 2016, 617, 1–54.
115. Z. Lin, B. R. Carvalho, E. Kahn, R. Lv, R. Rao, H. Terrones, M. A. Pimenta and M. Terrones, 2D Mater., 2016, 3, 22002.
116. Z. Dai, L. Liu and Z. Zhang, Adv. Mater., 2019, 1805417.
117. X. Zhou, J. Kalikka, X. Ji, L. Wu, Z. Song and R. E. Simpson, Adv. Mater., 2016, 28, 3007–3016.
118. J. Kalikka, X. Zhou, E. Dilcher, S. Wall, J. Li and R. E. Simpson, Nat. Commun., 2016, 7, 11983.
119. J. Jung, A. M. DaSilva, A. H. MacDonald and S. Adam, Nat. Commun., 2015, 6, 6308.
120. P. San-Jose, A. Gutiérrez-Rubio, M. Sturla and F. Guinea, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 75428.
121. M. M. Van Wijk, A. Schuring, M. I. Katsnelson and A. Fasolino, Phys. Rev. Lett., 2014, 113, 135504.
122. F. Guinea, M. I. Katsnelson and A. K. Geim, Nat. Phys., 2010, 6, 30.
123. D. Nandwana and E. Ertekin, Nano Lett., 2015, 15, 1468–1475.
124. A. De Sanctis, J. D. Mehew, S. Alkhalifa, F. Withers, M. F. Craciun and S. Russo, Nano Lett., 2018, 18, 7919–7926.
125. J. Quereda, P. San-Jose, V. Parente, L. Vaquero-Garzon, A. J. Molina-Mendoza, N. Agrät, G. Rubio-Bollinger, F. Guinea, R. Roldán and A. Castellanos-Gomez, Nano Lett., 2016, 16, 2931–2937.
126. S. Xie, L. Tu, Y. Han, L. Huang, K. Kang, K. U. Lao, P. Poddar, C. Park, D. A. Muller and R. A. DiStasio, et al. , Science, 2018, 359, 1131–1136.
127. W. Zhou, Y.-Y. Zhang, J. Chen, D. Li, J. Zhou, Z. Liu, M. F. Chisholm, S. T. Pantelides and K. P. Loh, Sci. Adv., 2018, 4, eaap9096.
128. H. Li, A. W. Contryman, X. Qian, S. M. Ardakani, Y. Gong, X. Wang, J. M. Weisse, C. H. Lee, J. Zhao and P. M. Ajayan, et al. , Nat. Commun., 2015, 6, 7381.
129. X. Xie, J. Kang, W. Cao, J. H. Chu, Y. Gong, P. M. Ajayan and K. Banerjee, Sci. Rep., 2017, 7, 9965.
130. Y. Zhang, Y. Kim, M. J. Gilbert and N. Mason, npj 2D Mater. Appl., 2018, 2, 31.
131. A. Pálinkás, P. Süle, M. Szendrő, G. Molnár, C. Hwang, L. P. Biró and Z. Osváth, Carbon N. Y., 2016, 107, 792–799.
132. B. S. Jessen, L. Gammelgaard, M. R. Thomsen, D. M. A. Mackenzie, J. D. Thomsen, J. M. Caridad, E. Duegaard, K. Watanabe, T. Taniguchi and T. J. Booth, et al. , Nat. Nanotechnol., 2019, 1.
133. C. Forsythe, X. Zhou, K. Watanabe, T. Taniguchi, A. Pasupathy, P. Moon, M. Koshino, P. Kim and C. R. Dean, Nat. Nanotechnol., 2018, 13, 566.

---