Revision of the International System of Units (Background paper)
Analytical Methods Committee AMCTB No 86
First published on 13th March 2019
Abstract
The International System of Units (SI) is the only globally agreed practical system of measurement units. Stemming from the Metre Convention of 1875, which established a permanent organisational structure for member governments to act in common accord on all matters relating to units of measurement, the SI was formalised in 1960 and defined by the ‘SI Brochure’. The foundation of the SI are the set of seven well defined base units: the metre, the kilogram, the second, the ampere, the kelvin, the mole, and the candela, from which all derived units (such as metres per second) are formed. On 16 November 2018 the 26th General Conference on Weights and Measures (CGPM) met, at an open meeting at the Palais des Congrès, Versailles, to discuss and vote on the re-definition of four of the SI’s seven base units: the mole, the ampere, the kelvin, and the kilogram. This change, effective from World Metrology Day (20 May) 2019, is perhaps the most fundamental change in the SI since its inception. For the first time the SI will be defined entirely in terms of fundamental physical constants, instead of requiring the maintenance of a physical artefact. This technical brief explains why this re-definition came about. No practical implications of the change are envisaged for analytical chemistry in the short term and improvements in measurement may take some time to realise.
The current International System of Units (SI) and the need for change
Measurement units were originally defined by physical artefacts or properties of specific materials. However such physical artefacts have obvious drawbacks in terms of their stability and susceptibility to damage and decay. It is preferable to have units defined in terms of constants of nature – so called ‘defining constants’ – which can be assumed to be invariant and can provide the greater accuracy demanded by today’s technology. As a result all the original unique physical artefacts which defined units have now all been superseded, apart from one, the kilogram.The kilogram remained the only base unit defined and realised as a single material artefact – the international prototype of the kilogram (IPK) – a platinum-iridium cylinder with a mass of exactly 1 kg, by definition, to which all mass measurements across the world are ultimately traceable and have been since 1889. For a long time metrologists have been keen to redefine the kilogram in terms of constants of nature. The development of the Kibble balance – a device invented by Dr Bryan Kibble (at the UK’s National Physical Laboratory) which allows mechanical and electrical force to be accurately compared – brought this possibility into sharper focus and also prompted additional proposals to redefine three other base units of the SI with respect to ‘defining constants’; the ampere, the kelvin and the mole (Mills et al., 2006; I. A. Robinson and S. Schlamminger, 2016). The metre was redefined in 1983 with respect to the speed of light, and the second has, since 1967, depended on a material property – a spectroscopic transition of a caesium-133 atom. The candela, dependent on the luminous efficacy technical constant related to a spectral response of the human eye, was not directly part of discussions to revise the SI.
In considering which constants could have their numerical values† fixed to redefine the kilogram it was important to ensure the relationship between quantities remained unaltered regardless of the choice of unit definition. A key equation, eqn (1), in these considerations, demonstrating how the Planck constant, h, and the Avogadro constant, NA, are closely linked, is given by rearranging the relationship that defines the Rydberg constant (a physical constant relating to atomic spectra):
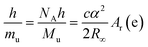 | (1) |
Considering that h is related to macroscopic mass via the Kibble balance experiment, and NA is related to macroscopic mass via the Avogadro experiment‡(Bartl, et al., 2017) it is clearly possible to define mass in terms of either of these constants. The corollary to this was that a new definition of the mole, based on a fixed numerical value of NA, was also likely.
Time for change
At the point of redefinition of any unit it is essential that the size of the unit does not change, and furthermore that the new definition is an improvement on the old definition. In the case of the kilogram (and therefore the mole) the limitation in the old definition was the drift in the mass of IPK over time. This cannot be measured directly since the mass of the IPK is always 1 kg by definition! However it may be estimated by comparison over time against its copies (IPK has only been removed from the safe in which it is kept on three occasions since 1889: 1946, 1991 and 2014) and by the behaviour of similar mass standards. These considerations resulted in international agreement that once three independent experiments (two or more Kibble balances and the Avogadro experiment) provided consistent results with an uncertainty of less than 5 parts in 108, a change would be beneficial. These conditions were met in time for a resolution to be brought before the 26th CGPM to propose revision of the SI according to fixed numerical values of seven ‘defining constants’ including redefinition of the kilogram, the mole, the ampere and the kelvin in terms of a fixed numerical value of the Planck constant, Avogadro constant, the elementary charge and the Boltzmann constant, respectively. Whilst the definitions of the second, metre and ampere will not change, they will be written in a different form to make them consistent with the new definitions for the units that will change. The resolution was unanimously approved on 16 November 2018, with an effective date of 20 May 2019. The delay between decision and implementation allows more widespread communication of the change to stakeholders, especially in the electrical area where there will be a small step change in the size of the ampere (about 1 part in 10 million). The seven defining constants of the SI from 20 May 2019 are shown in Table 1.| Symbol | Name | Numerical value | SI unit |
|---|---|---|---|
| ΔνCs | Hyperfine transition frequency of Cs | 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192 192![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 631 631![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 770 770 |
Hz |
| c | The speed of light in vacuum | 299![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 792 792![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 458 458 |
m s−1 |
| h | Planck constant | 6.62607015 × 10−34 | J s |
| e | Elementary charge | 1.602176634 × 10−19 | C |
| k | Boltzmann constant | 1.380649 × 10−23 | J K−1 |
| N A | Avogadro constant | 6.02214076 × 1023 | mol−1 |
| K cd | Luminous efficacy | 683 | lm W−1 |
The effects of redefinition for the mole and chemical measurement
The current definition refers to the mole containing as many elementary entities as there are atoms in 0.012 kilogram of carbon 12. Therefore currently we only know implicitly how many elementary entities this is by using a measure of an exact mass of a known material as a surrogate. The new definition removes this ambiguity, and reliance of the mole on the kilogram, by stating an exact number of elementary entities explicitly:“The mole, symbol mol, is the SI unit of amount of substance. One mole contains exactly 6.02214076 × 1023 elementary entities. This number is the fixed numerical value of the Avogadro constant, NA, when expressed in the unit mol−1 and is called the Avogadro number. The amount of substance, symbol n, of a system is a measure of the number of specified elementary entities. An elementary entity may be an atom, a molecule, an ion, an electron, any other particle or specified group of particles.”
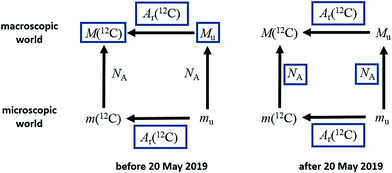
This definition is worded in the ‘explicit constant’ format that all SI base units will adopt following the revision of the SI. The implications of the change for the mole, shown in Fig. 1, are that the uncertainty previously associated with the Avogadro constant will disappear, and the molar mass of 12C and the molar mass constant – previously known exactly – will acquire a relative standard uncertainty equal to that of NAh at the time of redefinition, namely 4.5 × 10−10, and that in the future their values will be determined experimentally.
There are some immediate notional benefits of the redefinition of the mole:
• The reliance of the mole on the kilogram is removed;
• The relative uncertainty of the atomic mass and molar mass scales are equalised;
• The mole is no longer dependent on a material property and is more universal in its applicability;
• It reflects the way most chemists already consider the mole;
• The new definition may prove easier to teach;
• It is a better fit with 21st century technologies and keeps chemical metrology aligned with the rest of the SI.
Relative atomic masses and relative molecular masses are ratios, not dependent on the current definition of the kilogram, and will be unaffected by the proposed new definitions of the kilogram and the mole.
The relative uncertainties associated with the quantities involved in the mole redefinition are still several orders of magnitude smaller than those associated with the practical realisation of chemical quantities, which mostly occurs by weighing materials of known purity. As a result no practical implications of the change are envisaged for analytical chemistry in the short term and improvements may take some time to realise. However, the change is overall of benefit for chemistry in the longer term, paving the way for more accurate chemical measurement in future, particularly at ultra-low amounts of substance.
Wider benefits of revision of the SI
Aside from removing the last unique physical artefact from the SI, the new definitions in terms of fixed numerical values of defining constants are more universal in their applicability and more consistent with twenty first century technologies. The way to realise a unit is no longer implicitly or explicitly suggested by its definition. This separation future-proofs the unit definitions, ensuring that unit realisations will be able to benefit from all relevant future advances in technology and lays the foundations for more accurate measurements for all stakeholders for decades to come.Further reading
I. A. Robinson and S. Schlamminger, The watt or Kibble balance: a technique for implementing the new SI definition of the unit of mass, Metrologia, 2016, 53, A46–A74.I. M. Mills, P. J. Mohr, T. J. Quinn, B. N. Taylor and E. R. Williams, Redefinition of the kilogram, ampere, kelvin and mole: a proposed approach to implementing CIPM recommendation 1 (CI-2005), Metrologia, 2006, 43, 227–246.
G. Bartl, P. Becker, B. Beckhoff, H. Bettin, E. Beyer, M. Borys, I. Busch, L. Cibik, G. D’Agostino, E. Darlatt, M. Di Luzio, K. Fujii, H. Fujimoto, K. Fujita, M. Kolbe, M. Krumrey, N. Kuramoto, E. Massa, M. Mecke, S. Mizushima, M. Müller, T. Narukawa, A. Nicolaus, A. Pramann, D. Rauch, O. Rienitz, C. P. Sasso, A. Stopic, R. Stosch, A. Waseda, S. Wundrack, L. Zhang and X. W. Zhang, A new 28Si single crystal: counting the atoms for the new kilogram definition, Metrologia, 2017, 54, 693–715.
Resolution 1 of the 26th CGPM, 2018, https://www.bipm.org/en/CGPM/db/26/1/.
M. J. T. Milton and I. M. Mills, Amount of substance and the proposed redefinition of the mole, Metrologia, 2009, 46, 332–338.
Dr Richard J. C. Brown (National Physical Laboratory).
This Technical Brief was prepared on behalf of the AMC, and was approved by the AMC on 28 January 2019.
Footnotes |
| † The value of a quantity, Q, is expressed as the product of a numerical value, {Q}, and a unit, [Q]. Thus, Q = {Q}[Q]. The speed of light is a constant of nature with a value Qc which is fixed, and is not for us to choose. However, we are free to assign a fixed numerical value to the speed of light {Qc}, which thereby defines the size of the unit [Qc] for speed, in m s−1, since both of the other terms in the equation are fixed. This approach is analogous to all other unit definitions based on fixed numerical values of ‘defining constants’. |
| ‡ Sometimes called the X-ray crystal density (XRCD) experiment – an international consortium to count atoms in a near perfect silicon sphere. |
| This journal is © The Royal Society of Chemistry 2019 |