Open Access Article
Open Access ArticleInvestigation of cavitation-induced damage on PDMS films
Alex H.
Wrede
 a,
Faisal
Al-Masri
a,
Reza
Montazami
a,
Faisal
Al-Masri
a,
Reza
Montazami
 a and
Nicole N.
Hashemi
a and
Nicole N.
Hashemi
 *ab
*ab
aDepartment of Mechanical Engineering, Iowa State University, Ames, Iowa 50011, USA. E-mail: nastaran@iastate.edu
bDepartment of Biomedical Sciences, Iowa State University, Ames, IA 50011, USA
First published on 29th August 2019
Abstract
Traumatic brain injuries (TBIs) are complex phenomena that create epidemic healthcare and financial concerns. Recent studies have theorized that cavitation exists during a TBI and has potential to induce significant damage to the surrounding anatomy. This study seeks to implement polydimethylsiloxane (PDMS) films as a placeholder of the brain to elucidate the damage that the surrounding brain tissue would experience from nearby cavitation. The apparatus includes an existing methodology that implements controlled cavitation. 3D confocal microscopy and interferometry techniques are used to characterize the surface damage to the PDMS films. Visual representation and roughness parameters on the nanoscale help elucidate a distinct difference between control and experimental samples. These results help legitimize the concern of cavitation in the skull and also help motivate future studies to analyze the cellular response to surrounding cavitation.
1. Introduction
Despite decades of research, the brain continues to be one of the most obscure parts of the human body. TBI is the damaging aftermath to the brain due to a mechanical force, leading to functionality impairment. Exposure to blasts has led to TBI in over 60% of soldiers serving in Iraq and Afghanistan.1 Everyone in society is susceptible to TBI; this diagnosis is typical in falls and automobile collisions. TBIs are also prevalent in contact sports where athletes are often exposed to cranial impacts.2 There are many different leading causes and brain response mechanisms to TBI damage.3,4 Recent studies suggest the presence of cavitation in the human skull as a result of a TBI, which can arise due to the presence of small pockets of vapor in the cerebrospinal fluid (CSF).5–10 Upon impact, these vapor contents expand and collapse due to a low pressure wave that reflects off the skull boundary after the initial compressive wave travels through the skull.11 Cavitation has been proven to lead to significant erosion in alloys and hard plastics, applying a force that has been broadly characterized to a broad magnitude of 0.1–20 MPa.12–16 Although the degree of cavitation exposure likely differs between varying applications, if cavitation has the ability to erode steel, its potential to cause damage on the surrounding brain tissue is alarming.In this study, we investigate the topographical changes that cavitation induces to PDMS films to help illustrate the damage that cavitation has on brain tissue. Soft materials have been consistently used to model organs in vitro and in tissue engineering.17 Soft polymers have been a common candidate for this as they are easy and affordable to manufacture, and their elastic properties can be easily altered and studied.18 Adjusting the base to curing agent ratio in the PDMS fabrication process allows for arbitrary selection of the mechanical properties of PDMS.
The apparatus used to create cavitation on the PDMS films is similar to that used in previous studies.19 This method is advantageous because it allows for controlled cavitation, enabling a similar cavitation exposure from one sample to the next. Characterization of cavitation aftermath is conducted using 3D confocal microscopy and interferometry methods. This analysis yields novelty in multiple research disciplines, like propulsion and hydrodynamic pumping, but in the TBI realm, it helps unmask the physical detriments that cavitation has on the nearby neuronal anatomy. Understanding this aftermath is a vital piece to advance TBI recovery, prevention, and care.
2. Experimental
2.1 PDMS fabrication and cavitation apparatus
PDMS samples were prepared by mixing the base and curing agent (Sylgard 184, Dow Corning, Midland, MI) at a 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio and allowing them to cure at room temperature for 48 hours. Controlling the mass ratio of the base to curing agent affects the hardness of PDMS with higher ratios producing softer PDMS. The hardness of the PDMS samples is ∼50 shore (PHT-960, Phase II, Upper Saddle River, NJ), which is comparable to that of the human brain which has been measured to be 10–30 shore in previous studies.20 Also, the known elastic modulus of a similar PDMS sample measured at 560 kPa.21 The known elastic modulus of a human brain ranges between 694 Pa (ref. 22) and 9.2 kPa.23 Each PDMS sample was collected and cured in a 36 mm Petri dish. The thickness of all the PDMS films was 3–6 mm.
1 ratio and allowing them to cure at room temperature for 48 hours. Controlling the mass ratio of the base to curing agent affects the hardness of PDMS with higher ratios producing softer PDMS. The hardness of the PDMS samples is ∼50 shore (PHT-960, Phase II, Upper Saddle River, NJ), which is comparable to that of the human brain which has been measured to be 10–30 shore in previous studies.20 Also, the known elastic modulus of a similar PDMS sample measured at 560 kPa.21 The known elastic modulus of a human brain ranges between 694 Pa (ref. 22) and 9.2 kPa.23 Each PDMS sample was collected and cured in a 36 mm Petri dish. The thickness of all the PDMS films was 3–6 mm.
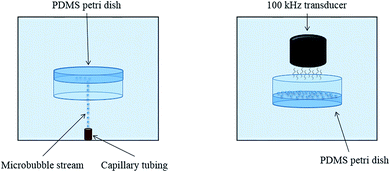
The complete apparatus configuration followed closely the adhesion technique outlined in previous studies and is illustrated in Fig. 1.7 This previously developed apparatus methodology is novel due to its level of control and efficiency in creating controlled cavitation. A 1.5 gallon tank is filled with deionized water and used to house the primary components of the apparatus. The PDMS-filled Petri dishes initially faced downward and were suspended mid-solution using a 3-axis stage (MT1, Thor Labs, Newton, New Jersey). Microbubbles (MBs) were produced by pushing air through a capillary tubing that had an inner diameter of 5 μm (Molex, Lisle, IL). The stream of rising MBs which was released from the tubing was oriented in the same plane as PDMS films. MBs exited the capillary tubing at a rate of ∼75 MB per min. The adhered MBs for this study had a diameter of ∼65 μm, similar to what is believed to exist in vivo, but altering capillary tubing size is directly correlated to the size of the outputted MBs.3 Air was used to make the MBs in this study due to its similar composition to CSF.7 For each trial, 450–500 MBs were collected across the exposed PDMS surface. The degree of cavitation presence in vivo is largely unknown; using 450–500 adhered MBs is a proof of concept and the amount of adhered MBs can arbitrarily be altered as in vivo cavitation is further researched and characterized. After MB collection, the PDMS sample was then moved out of plane with the rising MBs and rotated 180° so that it was exposed to an ultrasonic transducer, similar to the orientation shown in Fig. 1.24 The activation of the transducer creates resonant conditions for the collected MBs and ultimately induces cavitation (100 kHz center frequency, 5 cycles, pulse repetition frequency 59 Hz, 260 Vpp). The necessary amplification of the transducer signal is generated through the implementation of a power amplifier (E&I, 1140LA). The process of collecting MBs, rotating the PDMS substrate, and inducing cavitation was done ten times for each sample. Control samples were submerged in the tank and exposed to the transducer signal but they did not have any adhered MBs, eliminating the occurrence of cavitation. The control samples experienced ultrasound exposure to ensure that any observed topographical differences were solely due to cavitation forces.
2.2 Topography analytics
Topographical analysis was conducted using 3D confocal microscopy and interferometry techniques (S neox, Sensofar, Barcelona, Spain). Compatible software (SensoSCAN v6.3) calculates roughness parameters that provide detailed characteristics of the sample topography. These parameters are useful when deciphering the difference between surface impurities, noise, and cavitation damage. All 3D confocal microscopy trials were conducted using a 150× objective lens, red light, and 60% lighting. Interferometry methods employed a 50XDi objective lens, green light, and 15% lighting. Both of these methods are used to legitimize topographical summaries of the PDMS surfaces on the nanoscale.3. Results and discussion
3.1 3D confocal microscopy
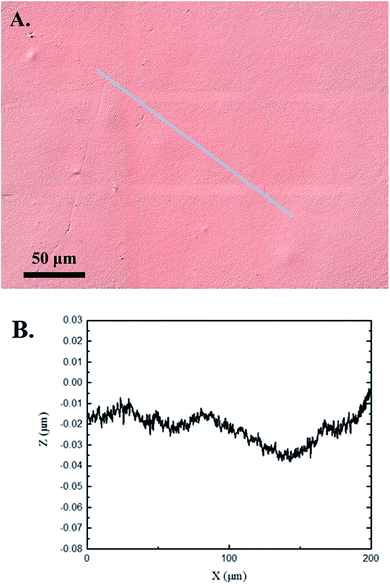
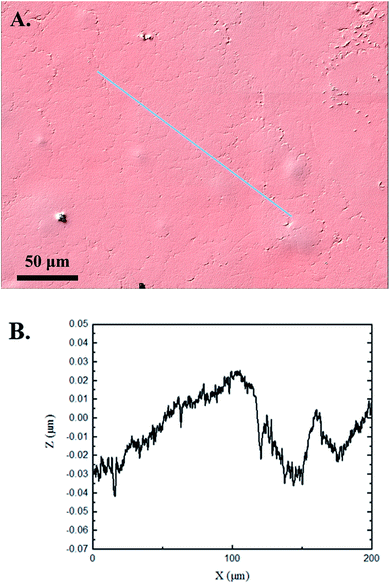
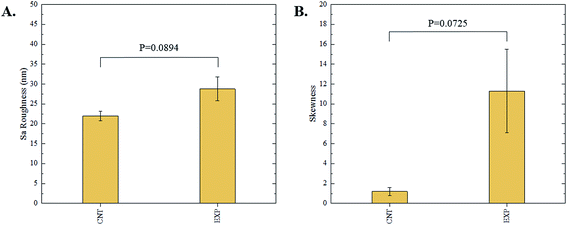
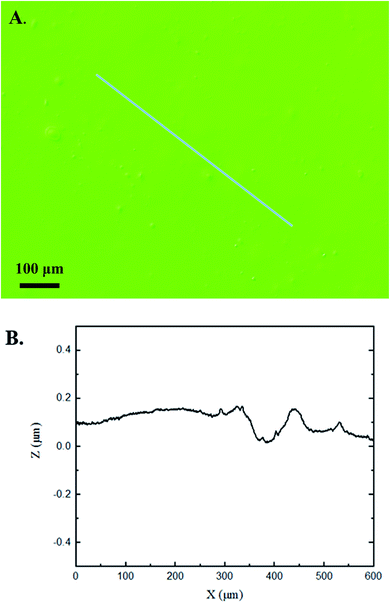
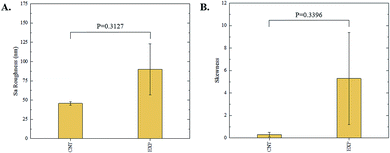
The 3D confocal microscopy system has an assortment of capabilities and objective options. Fig. 2 represents a typical illustration of the surface of a control sample. Using a 150× objective lens condenses the dimensions of the field of view significantly. A stitched 3 × 3 field scan is implemented to collect data across a larger area and eliminate any bias from one particular region. Fig. 3 illustrates the typical topography of an experimental sample after experiencing the surrounding cavitation. A visual comparison yields distinct differences in the nature of the surface between the two samples. It appears that the cavitation has a created wear and erosion-like effects as small tears are visible on the surface of PDMS. This damage is consistently visually present in the experimental samples and absent in the control samples. The damage from cavitation is further elucidated through roughness parameters that are internally calculated in the software. The roughness parameter ‘Sa’ is used to portray the overall roughness of the surface by calculating the magnitude of the difference in height from the mean height. The Sa calculation gives an optimal description of the surface roughness due to the fact that in the derivation, impurities or foreign objects adhered to the surface have a minimal effect on the final value.25 The average Sa value for all the control surfaces was calculated to be 22.0 nm. This value is noticeably different from the experimental samples, which had an average Sa value of 28.8 nm. This increase in roughness is expected due to the cavitation damage that is introduced.The skewness (Ssk) is a dimensionless roughness parameter that also helps characterize the topography changes. A positive value of Ssk describes a height distribution that is below the mean plane, that is, the valleys create more of a bias than the peaks. A negative Ssk value resembles a bias toward the peaks in the sample. Our hypothesis was that cavitation would create cavities on the surface, yielding a positive Ssk value. Hypothetically the control samples would ideally have a Ssk value at or around zero, but this may slightly fluctuate due to natural impurities on the surface or minor ultrasound damage. The results align with our hypothesis with a control and experimental average Ssk value of 1.1 and 11.3, respectively. The positive Ssk value for the control sample is likely due to impurities that exist on the nanoscale during the curing process of PDMS.26 The large Ssk value from the experimental samples points directly to an outside force creating erosion of the surface, similar to our anticipated hypothesis. This large Ssk also points to apparent cavitation damage because any debris or added noise that adheres to the surface by introducing the samples into the 1.5 gallon tank should cause a negative Ssk trend because they create peaks in the topography, but the cavitation erosion overrides this noise and remains biased below the mean height plane. Fig. 4 highlights the collected Sa and Ssk values from the control and experimental samples using 3D confocal microscopy. The p-values are also included to summarize the statistical significance of the data.
3.2 Interferometry
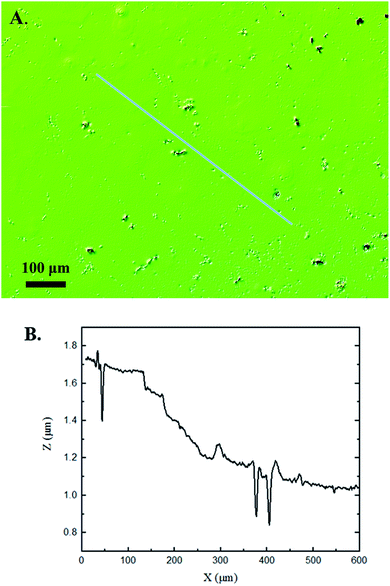
Interferometry methods offer another optical method for investigating and upholding the differences shown between the control and experimental samples in the 3D confocal microscopy methods. Fig. 5 and 6 show illustrations of a typical control and experimental sample, respectively, via interferometry. Similar to 3D confocal microscopy, there is an apparent difference in the visual representation of the two surfaces. Noticeable wear and erosion are present on the experimental sample. Fig. 5B and 6B graphically represent the height of the surface along an arbitrary path. Both samples show noise and fluctuation in the surface height but only the experimental sample shows any sharp changes in the negative z-direction. This is significant because cavitation is theorized to cause nanoscale cavities with similar dimensions in other biomedical applications.23 Any dust or debris added to the surface through the controlled cavitation process should show an additive height, not a subtractive difference. As a reminder, the control samples experience ultrasound exposure so this comparative data also eliminate the possibility of ultrasound being the primary contributor to the formation of these cavities. In essence, cavitation seems to be the only logical source of the resulting porous characteristics of the surface. Using interferometry techniques, the average Sa values for control and experimental samples are 45.7 nm and 90.0 nm, respectively. Additionally, the average Ssk value for the control samples is 0.3, compared to an average Ssk value of 5.3 for experimental samples. Fig. 7 summarizes the Sa and Ssk results from the control and experimental samples using interferometry. The p-values are also included to summarize the statistical significance of the data. The large p-values for this application demonstrate that the topography is highly dependent on the degree of cavitation exposure that the field of view captures from one scan to the next. All in all, these trends demonstrate a rougher surface for experimental samples that have bias below the mean height plane, similar to the results from 3D confocal microscopy techniques.Some experimental samples from both 3D confocal microscopy and interferometry yield similar roughness parameters compared to the mean values of the control samples, while others show distinct changes. This is likely due to the random positioning of MB adherence and induced cavitation, which lead to varied damage across the PDMS films, hence a larger standard error of the mean for experimental samples. Topographical analytics were collected randomly across the samples in order to eliminate visual bias. Additionally, to achieve nanoscale resolution, the field of view is 250 × 360 μm2 and 680 × 980 μm2 for 3D confocal microscopy and interferometry, respectively. This area is 54% and 403% of the average areal displacement between MBs on the surface, respectively. Because each area captures varying cavitation exposure, there is an expected increased discrepancy between individual surface scans. The overall trends point to clear topographical differences between the control and experimental samples using both 3D confocal microscopy and interferometry. This proven surface damage to a soft polymer with a slightly higher hardness and elastic modulus of the human brain offers great novelty, yet also brings about alarming awareness to the application of TBIs.
Characterizing the response of cranial anatomy to the surrounding cavitation is the next step for future studies. The resulting pressure field from the ultrasound beam was measured to be 60–100 kPa while inducing cavitation. This is important because brain damage is known to exist when the pressure exceeds a threshold of 173–235 kPa.26 Using this apparatus in future biological testing confirms that any documented physical brain injury is primarily as a result of cavitation, not ultrasound exposure. Pharmacists can only provide the best treatment if the cellular response to this TBI phenomena is known. On top of this, if cellular damage shows catastrophic trends from cavitation exposure, then engineers now realize the importance of eliminating or minimizing the possibility of cavitation existence in helmet design. All in all, this study has demonstrated the detriments that cavitation has on soft surfaces and helped motivate the progression of TBI knowledge.
4. Conclusion
Cavitation is commonly known to exist and erode away nearby surfaces in a variety of applications, like propulsion and hydrodynamic pumping.12,13,16 Recent theories have concluded that cavitation exists in the brain during a TBI and has the potential to leave behind detrimental effects.5,6 This study uses an existing apparatus that simulates controlled cavitation and analyzes the damage that soft polymers undergo after exposure to the surrounding cavitation. Methods of 3D confocal microscopy and interferometry are used to study the surface topography of control and experimental samples. Comparative results conclude that induced cavitation leads to clear damage and erosion to a PDMS surface. Although the PDMS samples do not exactly replicate the damage that the human brain might experience, it is clear that damage occurs in our simulations and this raises concern for how detrimental cavitation is to vulnerable cranial anatomy. Future studies seek to focus on the response that neuronal cells have to similar simulations of controlled cavitation. Taken together, this study has clear novelty that helps unmask the highly unknown characteristics of TBIs, allowing for advancements in providing better care and treatment to its victims.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Timothy Bigelow for his help with ultrasound logistics and lending us a power amplification system. We also thank Curtis Mosher for his assistance and training with 3D confocal microscopy and interferometry. This work was supported by the Office of Naval Research (ONR) Grant N000141612246 and ONR Grant N000141712620.References
- A. Chanda, C. Callaway, C. Clifton and V. Unnikrishnan, Mech. Adv. Mater. Struct., 2018, 25, 1335–1341 CrossRef.
- S. T. DeKosky, M. D. Ikonomovic and S. Gandy, N. Engl. J. Med., 2010, 363, 1293–1296 CrossRef CAS PubMed.
- J. L. Zamanian, L. Xu, L. C. Foo, N. Nouri, L. Zhou, R. G. Giffard and B. A. Barres, J. Neurosci., 2012, 32, 6391–6410 CrossRef CAS PubMed.
- S. Bartyczak and W. Mock, J. Phys.: Conf. Ser., 2014, 500, 182003 CrossRef.
- J. Goeller, A. Wardlaw, D. Treichler, J. O'Bruba and G. Weiss, J. Neurotrauma, 2012, 29, 1970–1981 CrossRef PubMed.
- M. B. Panzer, B. S. Myers, B. P. Capehart and C. R. Bass, Ann. Biomed. Eng., 2012, 40, 1530–1544 CrossRef PubMed.
- S. Haniff and P. A. Taylor, Shock Waves, 2017, 27, 929–945 CrossRef.
- H. Acar, S. Çınar, M. Thunga, M. R. Kessler, N. Hashemi and R. Montazami, Adv. Funct. Mater., 2014, 24, 4135–4143 CrossRef CAS.
- Y.-T. Wu and A. Adnan, Sci. Rep., 2017, 7, 5323 CrossRef PubMed.
- W. Kang, A. Adnan, T. O'Shaughnessy and A. Bagchi, Acta Biomater., 2018, 67, 295–306 CrossRef CAS PubMed.
- P. A. Taylor, J. S. Ludwigsen and C. C. Ford, Brain Injury, 2014, 28, 879–895 CrossRef PubMed.
- B. Ji, X. Luo and Y. Wu, J. Mech. Sci. Technol., 2014, 28, 1339–1348 CrossRef.
- B. K. Sreedhar, S. K. Albert and A. B. Pandit, Wear, 2017, 372–373, 177–196 CrossRef CAS.
- M. Petkovšek and M. Dular, Wear, 2013, 300, 55–64 CrossRef.
- E. Herbert, S. Balibar and F. Caupin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 041603 CrossRef PubMed.
- L. Chernin and D. V. Val, Renewable Energy, 2017, 113, 688–696 CrossRef.
- K. Y. Lee and D. J. Mooney, Chem. Rev., 2001, 101, 1869–1880 CrossRef CAS PubMed.
- M. Cabello, M. Mozo, B. D. la Cerda, C. Aracil, F. J. Diaz-Corrales, F. Perdigones, L. Valdes-Sanchez, I. Relimpio, S. S. Bhattacharya and J. M. Quero, Sens. Actuators, B, 2019, 288, 337–346 CrossRef CAS.
- A. H. Wrede, A. Shah, M. C. McNamara, R. Montazami and N. N. Hashemi, Ultrason. Sonochem., 2018, 43, 114–119 CrossRef CAS PubMed.
- Z. Wang, A. A. Volinsky and N. D. Gallant, J. Appl. Polym. Sci., 2014, 131, 41050 CrossRef.
- O. Clatz, H. Delingette, I. Talos, A. J. Golby, R. Kikinis, F. A. Jolesz, N. Ayache and S. K. Warfield, IEEE Trans. Med. Imaging, 2005, 24, 1417–1427 Search PubMed.
- G. Soza, R. Grosso, C. Nimsky, P. Hastreiter, R. Fahlbusch and G. Greiner, Int. J. Med. Robot Comp., 2005, 1, 87–95 CrossRef CAS PubMed.
- Y. Zhou, K. Yang, J. Cui, J. Y. Ye and C. X. Deng, J. Controlled Release, 2012, 157, 103–111 CrossRef CAS PubMed.
- E. S. Gadelmawla, M. M. Koura, T. M. A. Maksoud, I. M. Elewa and H. H. Soliman, J. Mater. Process. Technol., 2002, 123, 133–145 CrossRef.
- C. Con and B. Cui, Nanoscale Res. Lett., 2013, 8, 394 CrossRef PubMed.
- C. Ward, M. Chan and A. Nahum, Intracranial Pressure–A Brain Injury Criterion, 24th Stapp Car Crash Conference, 1980, p. 24 Search PubMed.
| This journal is © The Royal Society of Chemistry 2019 |