A new matrix-matched calibration strategy for static headspace gas chromatography to enable high throughputs in pharmaceutical quality control laboratories
Abstract
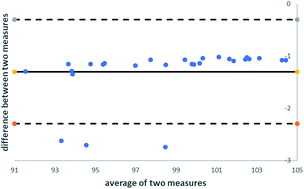
The analysis of residual solvents or generally, volatile organic substances using static headspace gas chromatography, is often accompanied by matrix effects. The standard addition method (SAM) is the calibration method of choice for circumvention of matrix effects because exactly the same sample matrix is present in both the calibration standard and the sample itself. However, the main disadvantages of the SAM are the large amounts of samples needed, the time-consuming sample preparation steps and long run times. To overcome these drawbacks by full compensation of matrix effects, a new calibration methodology was developed to combine the advantages of the external calibration and the standard addition methodologies. A comparison between the different calibration methods was performed using Bland–Altman plots and F- and t-tests. It was demonstrated that the application of the new calibration methodology leads to validatable methods in a more efficient way. A full validation according to the ICH Q2 guideline covering selectivity, linearity, limits of detection and quantification, system precision, repeatability, intermediate precision, and accuracy was successfully performed.


 Please wait while we load your content...
Please wait while we load your content...