Open Access Article
Open Access ArticlePlasticity in colloidal gel strands†
Joanne E.
Verweij
 ,
Frans A. M.
Leermakers
,
Joris
Sprakel
,
Frans A. M.
Leermakers
,
Joris
Sprakel
 and
Jasper
van der Gucht
*
and
Jasper
van der Gucht
*
Physical Chemistry and Soft Matter, Wageningen University, Stippeneng 4, 6708 WE, Wageningen, The Netherlands. E-mail: jasper.vandergucht@wur.nl
First published on 16th July 2019
Abstract
Colloidal gels are space-spanning networks of aggregated particles. The mechanical response of colloidal gels is governed, to a large extent, by the properties of the individual gel strands. To study how colloidal gels respond to repeated deformations, we perform Brownian dynamics simulations on single strands of aggregated colloidal particles. While current models assume that gel failure is due to the brittle rupture of gel strands, our simulations show that gel strands undergo large plastic deformations prior to breaking. Rearrangement of particles within the strands leads to plastic lengthening and softening of the strands, which may ultimately lead to strand necking and ductile failure. This failure mechanism occurs irrespective of the thickness and length of the strands and the range and strength of the interaction potential. Rupture of gel strands is more likely for long and thin strands and for a long-ranged interaction potential.
1 Introduction
Upon introducing an attractive interaction colloidal particles can aggregate and form a space-spanning network of dynamically arrested particles.1,2 Such a network, called a colloidal gel, behaves as an elastic solid that is able to withstand mechanical stress. Yet, when the applied stress exceeds the yield stress, the gel fluidizes and/or fractures and flows like a liquid.3–9 This combination of properties makes colloidal gels interesting for a variety of applications, including food products, cosmetics, and scaffolds for tissue engineering.10–14The macroscopic properties of colloidal gels, such as their elasticity and yielding behaviour, are intimately linked to the structure and connectivity of the particle network at the microscale.15–17 The main control parameters that determine the structure of a colloidal gel are the magnitude of the attraction strength between the particles,18–22 the particle volume fraction,18,21,22 and the shear history of the gel.23–25,44 In the limit of very strong attraction and very low volume fraction, irreversible aggregation leads to the formation of dilute, diffusion-limited fractal gels.18 In this regime, the mechanics and dynamics of the gel can be described using scaling approaches or by simulation models based on percolating networks of gel strands that ignore the internal structure of the strands.26–29 However, when the attraction strength is only a few times the thermal energy kBT, particle rearrangements can occur within the gel, leading to a much coarser gel structure formed by spinodal decomposition.19,20 The interplay between phase separation through spinodal decomposition and kinetic arrest then leads to very heterogeneous gels. As long as the volume fraction of particles is not too high (i.e. significantly below the colloidal glass transition), the microstructure of these gels consists of interconnected gel strands with a length and thickness that depends strongly on the interaction potential and the volume fraction.21,22
The linear elasticity of colloidal gels can be understood by considering the colloidal gel as a random network of gel strands, with an effective spring constant that depends on the thickness of the strands.30 However, the non-linear response of colloidal gels remains much less clear. Fracture and yielding of colloidal gels have been attributed to the brittle-like rupture of individual gel strands due to force-activated breaking of inter particle bonds.30,31 However, several authors have shown evidence that this picture may not be very accurate, and that failure of colloidal gels is preceded by significant plastic particle rearrangements.32–34 Recently we have shown, using a combination of rheological experiments and computer simulations, that these plastic rearrangements within gel strands lead to irreversible strand stretching and build-up of excess length, or slack, rather than strand rupture.35
Our results also suggested that the rheological response of colloidal gel networks can be understood by considering the mechanical and dynamic properties of the individual gel strands, which form the basic structural units of the gel (at least, at moderate volume fractions). To relate rheology to the structure of the colloidal gel, it is therefore necessary to know how the response of a gel strand depends on its thickness and length and on the interaction potential between the particles. Here, we will study this relation using computer simulations of gel strands under repeated deformation.
2 Method
We perform Brownian dynamics simulation to study the effect of repeated deformation on individual gel strands. We consider colloidal particles that interact through a Morse potential:36βu(r) = βε![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(ρ0[a − r])(exp[ρ0(a − r)] − 2) exp(ρ0[a − r])(exp[ρ0(a − r)] − 2) | (1) |
The motion of a particle i with position ri is obtained by solving the overdamped Langevin equation:
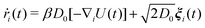 | (2) |
Gel strands are formed between two attractive flat walls. The parameters for the particle–wall interaction are the same as those for the particle–particle interactions, to make this interaction as inert as possible. The simulation box is periodic in the y- and z direction. The initial configuration of the gel strands is formed by placing a number of particles on a face centered cubic (fcc) lattice in a certain H × W × L, with H, W, and L the height, width, and length, respectively, expressed in numbers of particles. We consider nine types of gel strands that vary in thickness and length. For a thick gel strand, H = W = 5 particles (type A), for intermediate gel strands, H = W = 4 (type B), and for thin gel strands, H = W = 3 (type C). For each strand thickness, we consider three different lengths (specified as 1, 2, and 3), which gives the following number of particles for the different configurations: A1 = 200, B1 = 128, C1 = 77, A2 = 400, B2 = 256, C2 = 144, A3 = 600, B3 = 384 and C3 = 216. The equilibration time before applying oscillatory deformation is set to t = 568τB. As distances between particles in the initial configuration are larger than the range of the potential, particles aggregate randomly. Thus, the initial fcc lattice affects the approximate thickness of the gel strand but does not influence how particles are structured after equilibration. In Fig. 1 examples of these equilibrated gel strands are shown. The average thickness for each type of strand before deformation 〈D0〉 expressed in particle diameters equals 2.6, 2.0 and 1.4, respectively (see also eqn (4) below).
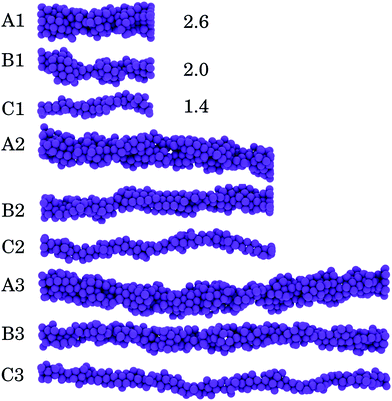 | ||
| Fig. 1 Visual representation of (A) thick, (B) intermediate and (C) thin strands before deformation. A2, B2 and C2, show strands that are 2× longer compared to A1, B1 and C1, whereas A3, B3 and A3 are 3× longer compared to the shortest strands. The average thickness of the start configurations 〈D0〉 (expressed in particle diameters) is indicated next to the strands (see eqn (4)). | ||
After equilibration, the gel strand is deformed through 14 oscillations in which the distance between the two walls is varied in a cyclic manner by moving the position of the left wall outwards. This leads to a sawtooth strain profile with a maximum strain γmax = 0.04 and a fixed strain rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.00284τB−1. Data for different amplitudes and strain rates are shown in the ESI† (Fig. S6 and S7). To make sure that observations are statistically relevant, each data point contains simulation data for at least 30 different gel strands. Here, we only consider strands that stay intact during the entire deformation.
= 0.00284τB−1. Data for different amplitudes and strain rates are shown in the ESI† (Fig. S6 and S7). To make sure that observations are statistically relevant, each data point contains simulation data for at least 30 different gel strands. Here, we only consider strands that stay intact during the entire deformation.
3 Results and discussion
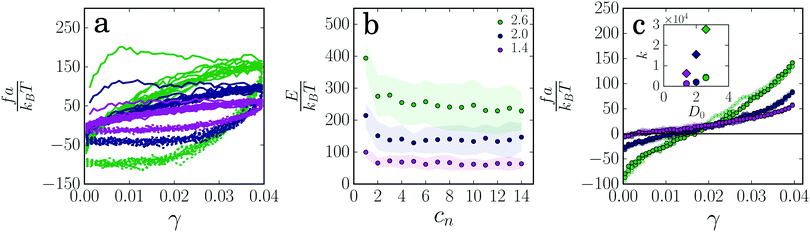
We cyclically deform the gel strands at constant strain rate and measure the resulting force f exerted on the walls. For strain cycles at small amplitude (γmax = 0.005), the force increases linearly with deformation, with a spring constant that increases with the strand thickness (ESI,† Fig. S2). However, for larger amplitude (γmax = 0.04), the force–strain curves are highly non-linear for all gel strands and show a pronounced hysteresis loop (Fig. 2a), which indicates significant energy dissipation during the deformation cycles. The dissipated energy is highest in the first deformation cycle (Fig. 2b), which is found to differ qualitatively from the subsequent cycles: the force first increases with increasing strain until a threshold value is reached, after which it levels off. This plateau in the force indicates plastic flow inside the gel strand due to irreversible particle rearrangements. The threshold force for plastic flow is proportional to the cross-section of the strands (ESI,† Fig. S3a), and increases with increasing strain rate (ESI,† Fig. S7), in agreement with models based on Kramers theory for force-activated dissociation of particle–particle bonds.37 As we have shown previously,35 the plastic rearrangements are associated with the irreversible stretching of the gel strand and the build-up of slack. Here, slack is defined as excess length that is created due to lengthening of the strands. This softens the gel strand, so that in subsequent cycles the observed force is lower than in the first cycle. The force–strain curve then quickly reaches a limit cycle, with an enclosed area that accounts for the viscoelastic dissipation due to reversible particle rearrangements. The dissipated energy is highest for the thick gel strands and lowest for the thin strands (Fig. 2b). As shown in ESI,† Fig. S3b, the dissipated energy is roughly proportional to the cross-section A of the strands, with each particle contributing 3–4% of the interaction energy ε to the energy dissipation. Increasing the strain amplitude from γmax = 0.04 to γmax = 0.06 (ESI,† Fig. S6) results in a single particle contribution of 5–6% of ε to the dissipated energy. The total energy dissipation thus scales with the applied strain amplitude and with the interaction energy.To analyze the softening of the gel strands in more detail, we disentangle the elastic and viscous contributions to the measured response by averaging the loading and unloading curve for each cycle.38 This averages out the viscous contribution, so that only the elastic contribution remains. The resulting elastic force goes through zero at a finite strain (Fig. 2c), which reflects the increase in the rest length due to the expansion cycles. The relative increase in rest length is highest for the thick strands (approximately 1.7%) and smallest for the thin strands (∼0.3%), indicating that thicker strands have more possibilities to deform plastically.
The plastic stretching of the gel strand leads to the build-up of slack. In subsequent deformation cycles, the slack induced in previous cycles is pulled out first, which results in little resistance and a strong decrease in the effective spring constant. Indeed, the effective spring constants measured after deforming the gel at a strain γmax = 0.04 is significantly smaller than those measured in the linear deformation regime (γmax = 0.005) (inset Fig. 2c). When the strain amplitude of the cycles becomes larger, the accumulated slack increases so that the effective spring constant decreases even further35 (see ESI,† Fig. S6). As expected, the spring constant increases with strand thickness and is approximately proportional to the cross-section of the strands (ESI,† Fig. S3c), indicating that each inter-particle bond contributes roughly equally to the spring constant.
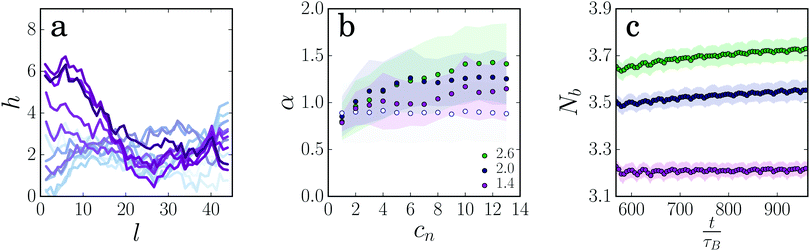
As the rest length of the gel strands increases in the loading cycle, it must be compressed in the return cycle. This could lead to bending or buckling of the strand. To investigate this, we follow the contour of the gel strand during the deformation cycles. We do this by dividing the strand into equally sized bins (σ = 0.9) and calculating the average coordinates in each bin.39 Since the ends of the strand are not fixed in our simulation, the strand fluctuates significantly, both during the deformation cycles and in rest (Fig. 3a). To analyze the shape of the strand and the amount of bending that occurs, we draw a line through the two ends of the strand and calculate the local distance of the contour from this straight line for each bin. The average distance over all bins α (Fig. 3b) is a measure for how much the shape of the gel strand deviates from a straight line, and indicates bending of the strand. For a gel strand that is not deformed, α does not change significantly, indicating that the shape of the gel strand remains more or less the same. However, when the gel strands are deformed α increases gradually with each deformation cycle, indicating that the strands must bend more to accommodate the increase in rest length. The increase in α is more pronounced for the thicker gel strands, which is in agreement with our observation that the thick strands show a larger increase in rest length upon deformation.§ Thus, thick strands are more prone to plastically elongate and develop slack, thereby contributing more strongly to this unusual non-linear response.
The internal rearrangements in the gel strands lead to the breaking and reformation of inter-particle bonds. Surprisingly, the average number of bonds per particle Nb increases as the strands are deformed and become longer (Fig. 3c). This suggests that the applied deformation leads to accelerated aging and coarsening of the gel strand, driving it gradually into a more favorable state by forming more inter-particle bonds.25,40 A similar strain-induced increase of the number of inter-particle bonds has been seen in computer simulations41 and in experiments24 on colloidal gel networks. We note that the strain-induced increase in the number of bonds is more pronounced and continues for a longer period as the gel strands get thicker (see also ESI,† Fig. S8b where data for even thicker gel strands are shown). This is further confirmed by the dissipated energy per cycle, which takes much longer to reach a plateau for thicker strands (ESI,† Fig. S8a). Again, this indicates that thick strands have more possibilities for local particle rearrangements and plastic deformation than thinner strands. The overall coarsening must imply that the deformation of the strands upon stretching occurs heterogeneously, so that thicker regions can form that are connected by thinner sections. This is reminiscent of the Rayleigh–Plateau instability in liquid jets (see Fig. 4b), and highlights the arrested liquid state of the colloidal gel. We further note that, even though the total number of bonds gradually increases, the force sustained by the strand does not increase. Our data suggests that this is because these newly formed bonds only stiffen the parts of the gel strand that are already strong, while the overall stiffness is determined mainly by the weak regions. A similar conclusion was obtained in recent computer simulations on large gel networks.41
 | ||
| Fig. 4 (a) Average mobility of the particles per oscillation (for strand types A2–C2). (b) Visual representation of particle displacements, highlighting the heterogeneity of the strain. | ||
We can further quantify the heterogeneity of the internal rearrangements by considering the displacement for each particle during a deformation cycle cn:
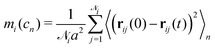 | (3) |
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) i is the number of nearest neighbours of particle i. Here, the average is taken over the entire oscillation.
i is the number of nearest neighbours of particle i. Here, the average is taken over the entire oscillation.
As shown in Fig. 4, particles in thin strands on average rearrange over larger distances compared to particles in thick strands. Upon deformation, many particles in a thin strand participate in movement, whereas only a few particles in the thicker strands move. Note, that the displacements of the particles contain both the elastic and plastic contributions. From the rest length of the strands we know that thick strands lengthen more and have a higher plastic deformation. Here, we see that these plastic deformations are indeed very heterogeneous and strongly localized to certain regions in the gel strand. The same heterogeneity is seen in thin strands, but these strands are also largely elastically deformed. The strong strain localization leads to the formation of thin necks, where the strand will eventually rupture.
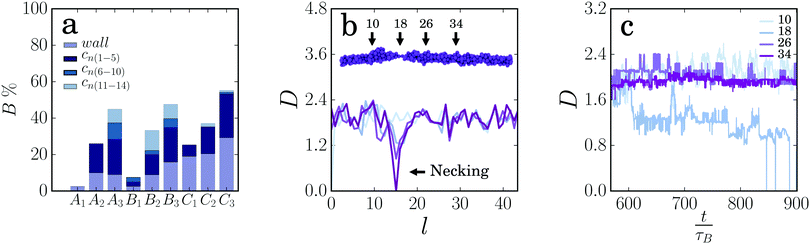
We also monitor strand rupture in our simulations and find that the percentage of broken gel strands increases strongly with increasing strand length and decreasing strand thickness (Fig. 5a). Long strands break more easily, because the probability that a weak spot forms during the deformation increases as strands get longer. Thin strands are held together by fewer inter-particle bonds, making them more prone to breakage. For the longest gel strands, the moment of rupture appears to shift to longer times as the strands get thicker: most of the thin strands (C3) rupture in the first cycles, while for the thicker strands (A3) rupture occurs more frequently in the later cycles, probably because more plastic deformation is needed before a sufficiently weak spot is formed. For the shorter strands, we do not observe such a trend, but this could be due to poor statistics, as the number of broken strands is much smaller for short chains. The fraction of broken gel strands also increases strongly with increasing strain amplitude (ESI,† Fig. S6), and with increasing strain rate (ESI,† Fig. S7), the latter indicating a transition to a more brittle response at higher rates due to fewer possibilities for plastic rearrangements.35 In the breakage statistics we specifically show the amount of breakage at the walls. This breakage does not dominate. Only for thin gel strands we see that the connection with the wall becomes a weak spot. We note that failure at the walls of the container is also observed experimentally in the yielding of some colloidal gels.5,6
To follow the ductile deformation leading to strand rupture, we consider the local thickness of the gel strand by dividing the strand into a number of segments and calculating the root-mean square thickness in each segment:42
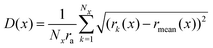 | (4) |
The necking process leading to strand fracture raises the question whether strand rupture occurs at pre-existing defects in the gel strands, formed during gel formation as suggested previously,30 or at random locations along the strand where plastic deformations happen to localize during deformation of the gel. In other words, is there a correlation between the thinnest region of the gel strand before deformation and the location where the strand finally breaks? To test this, we deform the initial configurations of 15 strands multiple times and monitor the initial thickness at the location where the strand is found to break. We find that the strand is indeed more likely to break at a thin region: the average initial thickness at the location of rupture, normalized by the average strand thickness, 〈Dbreak〉/〈D0〉 is 0.74, 0.82 and 0.82 for the thick, intermediate, and thin strands, respectively. Thus, strain localization and subsequent strand rupture tend to occur predominantly in low density regions of gel strands.
In 46% of the cases, thick strands break at the thinnest part Dmin of the start configuration. For intermediate and thin strands, this is only 37% and 18%, respectively. It can be concluded, therefore, that thick strands are more likely to break at a weak spot or defect in the original strand, while thin strands tend to break at more random locations. Previously, we noted that in thick strands only a few particles have large rearrangements at the weak spots. As a result, the initial structure of these strands is more likely to determine where failure will occur, in line with previous work.30
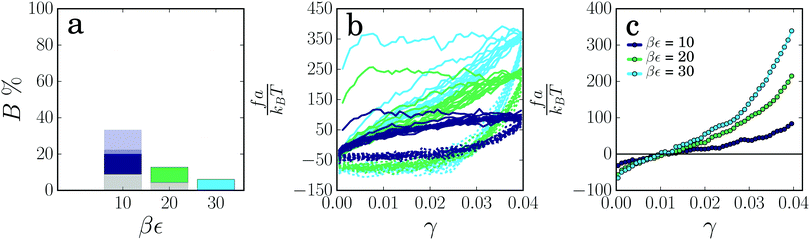
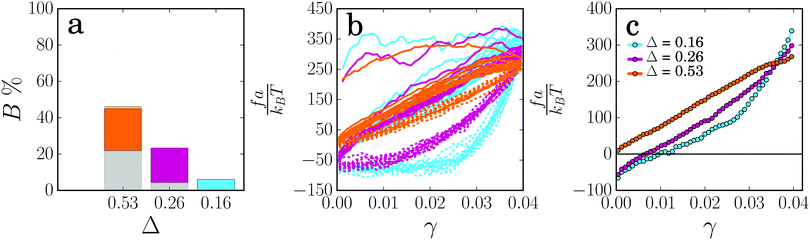
Now that we have shown how the thickness and length of colloidal gel strands affect their mechanical and plastic response, we consider the effect of the interaction potential between the particles (for potentials see ESI,† Fig. S1). Increasing the attraction strength between the particles makes the strands more resistant to rupture, as indicated by a lower percentage of broken strands (Fig. 6a). The force–strain relations for the different interaction energies show a similar plastic flow regime in the first deformation cycle, with a threshold force for plastic flow that increases approximately proportionally to the attraction strength (Fig. 6b). These findings are in agreement with theoretical models based on Kramers theory for force-activated bond rupture, which predict a rupture probability that decreases exponentially with the interaction strength and a threshold force that, for a given strain rate, is proportional to the effective spring constant and thus to the attraction strength ε.4,37,43 From the elastic contribution to the force, we observe that the change in rest length induced by the deformation cycles does not depend on the attraction strength (Fig. 6c). This indicates that the mechanism by which colloidal gels weaken due to local plasticity does not depend on the strength of the interaction, even when this attraction strength is as large as 30kBT. This is further confirmed by the amount of particle displacements, which is nearly independent of the attraction strength (ESI,† Fig. S4a), and the total dissipated energy in the cycles, which is proportional to the attraction strength (ESI,† Fig. S4b). The spring constant of the strands after the deformation cycles increases with increasing attraction energy (Fig. 6c), and after rescaling with ε, we find that the elastic contribution to the force is proportional to ε (ESI,† Fig. S4c).
In addition to varying the strength of the interactions, we also change the range of the attraction by changing the range parameter ρ0, giving well widths of approximately Δ = 0.528a, 0.264a, and 0.160a (for ρ0 = 10, 20, and 33 respectively) (see ESI,† Fig. S1). This is an interesting property to vary as the range over which interactions are sticky influences the deformation of the strands. Note that for simulations of a full colloidal gel a given pair potential and volume fraction ϕ gives an average length and thickness distribution of the gel strands. Here, we try to uncouple these two, by looking at strands of a single length and thickness with different pair potentials. To a certain extent this gives some ‘artificial’ effects, as in real gels the potential width and network structure are coupled. Still, we can show some interesting observations.
We find that increasing the range of the attraction makes the strands more prone to rupture (Fig. 7a). However, note that due to a larger potential width strands are aged substantially more (see ESI,† Fig. S5) and thus contain a higher number of weak spots.
The force–strain curves again look similar, showing a plastic flow regime in the first cycle. The threshold force for plastic deformation appears to be rather insensitive to the range of the attraction, while the amount of dissipated energy increases significantly as the attraction range decreases (ESI,† Fig. S5), reflecting a higher number of broken bonds. When looking at the elastic component of the force–strain curve for the deformed strands (Fig. 7c), we find a much larger increase in rest length for the shorter-ranged attraction. We thus conclude that plastic deformation, leading to strand stretching and softening, is more pronounced in gels with a short-ranged attraction, while a gel with long-ranged attraction only shows a linear deformation response at γmax = 0.04.
Note also that the stiffness of the deformed gel strands, as indicated by the slope of the force–strain curves in Fig. 7c, becomes almost independent of the attraction range. This might seem surprising, as the stiffness of a single bond is given by the second derivative of the potential, k ∼ ερ02 ∼ ε/Δ2, so that one would expect the highest stiffness for the smallest well width. Yet, we know that for small Δ the strand is plastically deformed and softening occurs, resulting in a decrease of the spring constant in the linear regime. The effective resulting stiffness is set by the threshold force f* where the plastic flow regime starts, keff ≈ f*/γmax.
4 Conclusions
Our results highlight how failure and yielding of colloidal gels result from plasticity at the scale of individual gel strands. While previous models for colloidal gel rheology and failure were based on the brittle rupture of gel strands, we show that this rupture is preceded by significant plastic deformations that cause irreversible lengthening and softening of gel strands. We observe this mechanism of failure for strands of different length and thickness and for interaction potentials of different strength and range, suggesting that it should be relevant for a wide range of experimental colloidal systems. Recently, we showed experimental results that support this finding.35 Our findings are also in agreement with earlier experiments that showed a two-step yielding in colloidal gels under shear;32 here, the first yielding event was attributed to restructuring and effective lengthening of gel elements in the shear direction, while the second step was attributed to strand rupture. Our results underpin this hypothesis and provide a microscopic mechanism. Furthermore, our results indicate that the amount of plastic deformation that a gel can undergo before it ruptures is determined by the structure of the gel and by the interaction potential. Coarser gels, consisting of short and thick gel strands, will deform much more plastically than dilute gels with long and thin strands. Plasticity is also promoted by a large attraction strength and a short attraction range.Our simulations have focused on single gel strands. While our recent results have shown that the macroscopic rheological properties of a colloidal gel can indeed be linked to the properties of the individual strands that constitute the gel,35 it remains an open question how the network topology influences the non-linear response. Combining our results for single strands with a full characterization of the network structure may be a first step towards a fully predictive model for colloidal gel rheology.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is part of the Industrial Partnership Programme Hybrid Soft Materials that is carried out under an agreement between Unilever Research and Development B.V. and the Netherlands Organisation for Scientific Research (NWO). JvdG acknowledges the European Research Council for financial support (ERC Consolidator grant Softbreak). The work of J. S. is part of the VIDI research programme with project number 723.016.001, which is financed by the Netherlands Organisation for Scientific Research (NWO).References
- E. Zaccarelli, J. Phys.: Condens. Matter, 2007, 19, 323101 CrossRef.
- V. Trappe and P. Sandkühler, Curr. Opin. Colloid Interface Sci., 2004, 8, 494–500 CrossRef CAS.
- B. J. Landrum, W. B. Russel and R. N. Zia, J. Rheol., 2016, 60, 783–807 CrossRef CAS.
- J. Sprakel, S. B. Lindström, T. E. Kodger and D. A. Weitz, Phys. Rev. Lett., 2011, 106, 248303 CrossRef PubMed.
- T. Gibaud, D. Frelat and S. Manneville, Soft Matter, 2010, 6, 3482–3488 RSC.
- T. Gibaud, C. Perge, S. B. Lindstrom, N. Taberlet and S. Manneville, Soft Matter, 2016, 12, 1701–1712 RSC.
- K. Masschaele, J. Fransaer and J. Vermant, J. Rheol., 2009, 53, 1437–1460 CrossRef CAS.
- V. Grenard, T. Divoux, N. Taberlet and S. Manneville, Soft Matter, 2014, 10, 1555–1571 RSC.
- C. Perge, N. Taberlet, T. Gibaud and S. Manneville, J. Rheol., 2014, 58, 1331–1357 CrossRef CAS.
- M. Diba, H. Wang, T. E. Kodger, S. Parsa and S. C. G. Leeuwenburgh, Adv. Mater., 2017, 29, 1604672 CrossRef PubMed.
- R. Mezzenga, P. Schurtenberger, A. Burbidge and M. Michel, Nat. Mater., 2005, 4, 729–740 CrossRef CAS PubMed.
- C. Das, M. G. Noro and P. D. Olmsted, Phys. Rev. Lett., 2013, 111, 148101 CrossRef PubMed.
- K. Y. Lee and D. J. Mooney, Chem. Rev., 2001, 101, 1869–1880 CrossRef CAS PubMed.
- A. Zemel, I. B. Bischofs and S. A. Safran, Phys. Rev. Lett., 2006, 97, 128103 CrossRef CAS PubMed.
- L. C. Hsiao, R. S. Newman, S. C. Glotzer and M. J. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2012, 16029–16034 CrossRef CAS PubMed.
- A. D. Dinsmore, V. Prasad, I. Y. Wong and D. A. Weitz, Phys. Rev. Lett., 2006, 96, 185502 CrossRef CAS PubMed.
- M. Bouzid, J. Colombo, L. V. Barbosa and E. Del Gado, Nat. Commun., 2017, 8, 15846 CrossRef CAS PubMed.
- S. Griffiths, F. Turci and C. P. Royall, J. Chem. Phys., 2017, 146, 014905 CrossRef PubMed.
- B. J. Landrum, W. B. Russel and R. N. Zia, J. Rheol., 2016, 60, 783–807 CrossRef CAS.
- P. J. Lu, E. Zaccarelli, F. Ciulla, A. B. Schofield, F. Sciortino and D. A. Weitz, Nature, 2008, 453, 499–503 CrossRef CAS PubMed.
- A. D. Dinsmore and D. A. Weitz, J. Phys.: Condens. Matter, 2002, 14, 7581 CrossRef CAS.
- V. Trappe, V. Prasad, L. Cipelletti, P. N. Segre and D. A. Weitz, Nature, 2001, 411, 772–775 CrossRef CAS PubMed.
- N. Koumakis, E. Moghimi, R. Besseling, W. C. K. Poon, J. F. Brady and G. Petekidis, Soft Matter, 2015, 11, 4640–4648 RSC.
- A. Helal, T. Divoux and G. H. McKinley, Phys. Rev. Appl., 2016, 6, 064004 CrossRef.
- E. Moghimi, A. R. Jacob, N. Koumakis and G. Petekidis, Soft Matter, 2017, 13, 2371–2383 RSC.
- Y. Kantor and I. Webman, Phys. Rev. Lett., 1984, 52, 1891 CrossRef.
- W.-H. Shih, W. Y. Shih, S.-I. Kim, J. Liu and I. A. Aksay, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 42, 4772 CrossRef CAS PubMed.
- A. Krall and D. Weitz, Phys. Rev. Lett., 1998, 80, 778–781 CrossRef CAS.
- E. Del Gado and W. Kob, J. Non-Newtonian Fluid Mech., 2008, 149, 28–33 CrossRef CAS.
- J. Conrad, H. Wyss, V. Trappe, S. Manley, K. Miyazaki, L. Kaufman, A. Schofield, D. R. Reichman and D. Weitz, J. Rheol., 2010, 54, 421–438 CrossRef CAS.
- S. B. Lindström, T. E. Kodger, J. Sprakel and D. A. Weitz, Soft Matter, 2012, 8, 3657–3664 RSC.
- H. K. Chan and A. Mohraz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 041403 CrossRef PubMed.
- V. Gopalakrishnan and C. Zukoski, J. Rheol., 2007, 51, 623–644 CrossRef CAS.
- S. Aime, L. Ramos and L. Cipelletti, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 3587–3592 CrossRef CAS PubMed.
- J. M. van Doorn, J. E. Verweij, J. Sprakel and J. van der Gucht, Phys. Rev. Lett., 2018, 120, 208005 CrossRef CAS PubMed.
- C. P. Royall, J. Eggers, A. Furukawa and H. Tanaka, Phys. Rev. Lett., 2015, 114, 258302 CrossRef PubMed.
- P. J. Skrzeszewska, J. Sprakel, F. A. de Wolf, R. Fokkink, M. A. C. Stuart and J. van der Gucht, Macromolecules, 2010, 43, 3542–3548 CrossRef CAS.
- S. Münster, L. M. Jawerth, B. A. Leslie, J. I. Weitz, B. Fabry and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 12197–12202 CrossRef PubMed.
- F. Gittes, B. Mickey, J. Nettleton and J. Howard, J. Cell Biol., 1993, 120, 923–934 CrossRef CAS PubMed.
- R. N. Zia, B. J. Landrum and W. B. Russel, J. Rheol., 2014, 58, 1121–1157 CrossRef CAS.
- J. Colombo and E. Del Gado, J. Rheol., 2014, 58, 1089–1116 CrossRef CAS.
- A. Grosberg and A. R. Hohlov, Statistical physics of macromolecules, Transl. by: Y. A. Atanov, AIP Press, Woodbury, NY, 1994 Search PubMed.
- B. O. Conchuir and A. Zaccone, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 032310 CrossRef.
- N. Koumakis and G. Petekidis, Soft Matter, 2011, 7, 2456–2470 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm00686a |
| ‡ To determine the inter-particle bonds, we will consider all particles that are within a distance corresponding to 1% of the original well depth (u(r) < 0.01ε) as bonded. When not mentioned otherwise, ρ0 equals 33. This corresponds to a well-width of approximately Δ = 0.16a. |
| § Although a gel strand is also allowed to move up and down along the walls we do not see an increase of the length of line l in subsequent oscillations. Thus, parameter α is a good measure to describe strand lengthening as a consequence of buckling. |
| This journal is © The Royal Society of Chemistry 2019 |