Open Access Article
Open Access ArticleAdsorption of nitrogen-containing compounds on hydroxylated α-quartz surfaces†
Oksana Tsendraab,
A. Daniel Boese *c,
Olexandr Isayevd,
Leonid Gorbef,
Andrea Michalkova Scottg,
Frances C. Hillg,
Mykola M. Ilchenkof,
Victor Lobanovb,
Danuta Leszczynskah and
Jerzy Leszczynski
*c,
Olexandr Isayevd,
Leonid Gorbef,
Andrea Michalkova Scottg,
Frances C. Hillg,
Mykola M. Ilchenkof,
Victor Lobanovb,
Danuta Leszczynskah and
Jerzy Leszczynski a
a
aInterdisciplinary Nanotoxicity Center, Department of Chemistry and Biochemistry, Jackson State University, 1400 Lynch Street, P. O. Box 17910, Jackson, MS 39217, USA
bChuiko Institute of Surface Chemistry, National Academy of Sciences of Ukraine, 17 General Naumov St., Kyiv 03164, Ukraine
cInstitute of Chemistry, Physical and Theoretical Chemistry, University of Graz, Heinrichstrasse 28/IV, 8010 Graz, Austria. E-mail: Adrian_Daniel.Boese@uni-graz.at
dUNC Eshelman School of Pharmacy, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599, USA
eHX5, LLC, Vicksburg, MS 39180, USA
fInstitute of Molecular Biology and Genetics, National Academy of Sciences of Ukraine, 150 Zabolotnogo St., Kyiv 03143, Ukraine
gU. S. Army Engineer Research and Development Center (ERDC), Vicksburg, MS 39180, USA
hDepartment of Civil and Environmental Engineering, Jackson State University, Jackson, MS 39217, USA
First published on 7th November 2019
Abstract
Adsorption energies of various nitrogen-containing compounds (specifically, 2,4,6-trinitrotoluene (TNT), 2,4-dinitrotoluene (DNT), 2,4-dinitroanisole (DNAn), and 3-nitro-1,2,4-triazole-5-one (NTO)) on the hydroxylated (001) and (100) α-quartz surfaces are computed. Different density functionals are utilized and both periodic as well as cluster approaches are applied. From the adsorption energies, partition coefficients on the considered α-quartz surfaces are derived. While TNT and DNT are preferably adsorbed on the (001) surface of α-quartz, NTO is rather located on both α-quartz surfaces.
Introduction
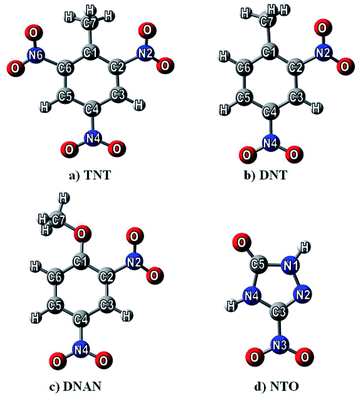
Nitrogen-containing compounds (NCCs) are chemically important species, as they are munitions constituents and emerging contaminants,1,2 representing a group of potentially hazardous pollutants.3,4 These will possibly spread to the environment during the production, processing, destruction, and recycling of drugs, dyes, pesticides, and energetic compounds. With this work, we would like to help to provide a virtual mesocosm to accurately predict how such chemical compounds will interact, move and degrade in variable natural environments.5,6 Here, adsorption on surfaces plays a significant role in the fate of such chemicals in nature. A detailed understanding of the chemistry of adsorbate and substrate for adsorption is needed to address the above questions. The influence of fluids at interfaces and the strength of the forces binding the adsorbed species are also essential considerations.Since experimental results on the adsorption of these species are difficult and rather sparse,7,8 we decided to study the adsorption abilities of these compounds computationally in order to predict the ecological impact of NCCs. The potentially hazardous contaminants computed are 2,4,6-trinitrotoluene (TNT), 2,4-dinitrotoluene (DNT), 2,4-dinitroanisole (DNAn), and 3-nitro-1,2,4-triazole-5-one (NTO) (see Fig. 1). Previous reports containing these species were devoted to prediction of nitro-aromatics reactivity,9 toxicity,10–12 environmentally important physical properties13–15 and adsorption abilities on various materials.16–21
Silica is one of the most abundant species on earth's crust and is most commonly found in the form of quartz. There is a plethora of studies of organic pollutants on silica, although in most cases mesoporous one.22–24 Mesoporous and amorphous silica incorporates many different planes and symmetries. In computations, very often only one surface is used, as it is time-demanding to construct and then compute several surfaces. Here, it is vital to study the adsorption of NCCs on several surfaces.
Previously, we have studied the adsorption of these compounds on the hydroxylated (100) surface.25 By going beyond the (100) surface, diverse effects are possible, and even the adsorption properties of different adsorbed species may vary with the different surface used. With various surfaces, different hydrogen bonds will be formed with the adsorbed molecules.26 As will be shown later in this study, the surface can have a rather large effect on the adsorption properties of larger molecules.
In our previous publication in which we investigated the (100) surface,25 the amount and the type of adsorption bonds and adsorption energies of TNT, DNT, DNAn, and NTO were analysed using density functional theory (DFT) and post-Hartree–Fock methods (Møller–Plesset perturbation theory MP2) utilizing a cluster approach, also embedding the clusters with the ONIOM method.27
The conclusions of the previous work were as follows:
(i) the cluster models, which included two oxygen–silicon–oxygen layers, were quantitatively enough to reproduce the most essential structural and energetic features of the NCCs adsorption (in other words: the application of larger number of ONIOM layers is not necessary);
(ii) inclusion of dispersion corrections into the applied DFT functionals (such as M06-2X and PBE) generated the energy of adsorption more comparable to other functionals and MP2, and suggested the preference of the “parallel” adsorbed molecule over the “perpendicular” one when a low coverage regime is considered. Our own,25 as well as other published data,28 suggested that for such surface interactions PBE + D3 level may be more accurate than M06-2X + D3 one.
This current study uses the same nitro-aromatic compounds as adsorbates and hydroxylated silica as adsorbent. It extends and complements the previous investigation in the following directions:
(i) The hydroxylated (001) quartz surface is considered as an important adsorbent due to having the largest surface energy of the (001), (110), (102), (111), (100), etc. quartz surfaces.29,30
(ii) For comparison, we also included models that apply periodic boundary conditions. The latter are capable of treating long-range electrostatic and dispersion effects, which are not captured by the finite cluster model.
(iii) The influence of temperature (computing the thermodynamics of adsorption) is now considered for both the (100) and the (001) α-quartz surfaces within the rigid-rotor-harmonic oscillator (RRHO) approximation.
From a theoretical point of view, hydroxylated surfaces are noteworthy, as they exhibit electrostatic and van-der-Waals interactions as well as form hydrogen bonds with the surfactants.
Methods
Periodic slab models
Periodic slab models were calculated using periodic boundary conditions (PBC) with the QuickStep module of the CP2K code.31 As functional, the generalized gradient approximation (GGA) functional PBE32 was used, while long range dispersion interactions were accounted for using the empirical van der Waals corrections of Grimme using D2.33 A hybrid Gaussian and plane wave (GPW) approach was employed-the wave functions were expanded in terms of Gaussian functions by utilizing a molecularly optimized, polarized basis set of triple-ζ quality (MOLOPT-TZVP).34 The core electrons were represented with norm-conserving Goedecker–Teter–Hutter (GTH) pseudopotentials,35 and the auxiliary plane-wave basis set was truncated with a 400 Ry energy cutoff.The surface was modelled using a slab approach with six silica layers. The geometry relaxation was performed without any constraints, with the NCC molecules adsorbed only on one side of the slab, with the standard CP2K dipole corrections used.36 The length of the cell along the surface-molecule axis was chosen to be 40 Å in order to decouple the slabs from each other. Only the à point was used in the evaluation of the integrals over the first Brillouin zone, as a large bulk lattice constant of 15.18 Å obtained with periodic PBE + D2 was used for the surface plane.
Cluster models
Following the previous publication on the adsorption of NCC on silica (100),25 the structures and interaction energy values of the cluster were computed using various levels of DFT which included the M06-2X/6-31G**37–41 and PBE + D3/TZVPPD32,42–45 functional and basis set combinations. These calculations were performed using the Gaussian0946 and TURBOMOLE 6.3.147 program packages. Adsorption energies (Eads) were calculated as a difference between the total energy of the whole adsorption system and the adsorbate/adsorbent. To all energies, we added zero-point energies which were computed by analytical second derivatives and the harmonic oscillator approximation. Eads values were corrected for the basis set superposition error (BSSE) for which the counterpoise method was applied.48 The quartz-cluster geometry was kept frozen, while the surface hydroxyl groups and adsorbates were allowed to relax. The chemical formula of the (001) α-quartz cluster model is Si53O142H72. This formula results from 35 bulk SiO2 units, eight surface- and ten bottom-terminated SiO4 units. Dangling bonds of the outmost layers of the surface and towards the bulk phase were saturated with hydrogen atoms, whereas only surface hydrogen atoms are shown in Fig. 2–5.In order to analyse the bonding patterns of the individual hydrogen bonds, Bader's “Atoms in Molecules” approach (AIM)49 was employed using the AIM2000 program package.50 The specific type of the critical points between two contacts of the adsorbate and the adsorbent were computed together with the electron density (ρ). Within this approach, a bond is associated with the presence of a (3, −1) critical point of the electron density located between two atoms. Hydrogen bonds typically correspond to a small ρ and a large, positive Laplacian of the electron density (∇2ρ) at the BCP, whereas covalent, dative, or metallic bonds are characterized by a large ρ, and a large negative ∇2ρ. The energy of each bond formed between the adsorbate and adsorbent was further calculated using Espinosa's equation.51 We used EHB = V/2 between the local potential energy (V) and the H-bond energy (EHB) at the BCP to express the energy of an H-bond:
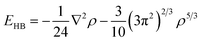 | (1) |
The energies of the intermolecular interactions calculated using this method correspond well with the energy values calculated with other quantum-chemical methods.52–54
Single point calculations
In addition, single point calculations including dispersion terms using the DFT + D3 program package by Grimme et al. and the TURBOMOLE program package were computed for all considered adsorption complexes obtained after optimization in the cluster approach with the methods described above. Both M06-2X + D3 and PBE + D3 density functionals were used in combination with the 6-31G** and TZVPPD basis sets to estimate the accuracy and deviation of the geometries.Thermodynamic parameters
The adsorption enthalpy (ΔHads), adsorption entropy ΔSads and Gibbs free energy (ΔGads) were calculated at room temperature using the Rigid Rotor – Harmonic Oscillator – ideal gas (RRHO) approximation based on the vibrational frequencies calculated at the temperatures 10, 25, 40, 60 °C and the pressure 1 atm. Both surfaces as well as adsorbate-surface systems have the same number of negative frequencies, and as such, the effects coming from these cancel. We corrected ΔHads and ΔGads by the RT volume work term due the loss of rotational and translational freedom of the molecule on a surface (like, see for example, ref. 55).The harmonic frequencies were corrected by a scaling factor of 1.0273.56 The Boltzmann expression has been used to obtain the partition coefficient of adsorption by:
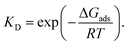 | (2) |
Results and discussion
Isolated silica surface model
Surface properties of silica materials cannot be explained by the density of OH-groups alone, as the properties of the different H-bond formed between the substrate and the surface play a major role. The hydrogen bonds on the surface by itself can be very different, depending on the crystalline plane.57–59 Hence, it was important to investigate the intra-surface H-bonds of the isolated α-quartz surface.The analysis of the (100) α-quartz cluster models25 of the surface suggests the presence of two types of intra-surface hydrogen bonds within the 10-membered cycles which differ significantly in strength: strong bonds are characterized by an energy larger than 10 kcal mol−1 and weak bonds have an energy of approximately 1 kcal mol−1. These bonds are perpendicular to each other (see Fig. 2).
 | ||
| Fig. 2 Optimized structure of (001) α-quartz surface and intra-surface H-bonds (HB1–HB10) as obtained from AIM analysis at the M06-2X/6-31G** level of theory (side and top view). The structures from the other approaches (namely, PBE + D3/6-31G** utilizing a cluster approach and PBE + D2 using PBC) can be found in the ESI, Fig. S1.† | ||
In order to compare to the results presented in ref. 25, we also analyzed the structure of the isolated cluster (001) obtained by M06-2X/6-31G**level calculations. The AIM data characterizing the hydrogen bonds presented in Fig. 2 are displayed in Table 1. The silanol groups of the (001) surface form a cooperative network which is significantly different from the (100) surface. In the paper (ref. 25), four hydrogen bonds of the (100) surface were found to be rather strong (more than −12.9 kcal mol−1). The other five bonds, however, were much weaker with −1.4 kcal mol−1 or less. According to the AIM analysis, the strength of the (001) surface hydrogen bonds ranges between −4 and −8 kcal mol−1 (Table 1). This can be compared to the values of the water dimer (−5.02 kcal mol−1) and the water–ammonia complex of −6.46 kcal mol−1.60 The 12-membered rings on the (001) surface are thus disrupted or perturbed more easily by the hydrogen bonds formed with the nitro functional groups during the adsorption of an NCC.
![[double bond splayed right]](https://www.rsc.org/images/entities/char_e00a.gif) O⋯H–O angles (°), bond energies (E(HB), kcal mol−1), electron density (ρ, au), and Laplacian of the electron density (∇2ρ, au) for the isolated model of the (001) surface of α-quartz optimized at the M06-2X/6-31G** level
O⋯H–O angles (°), bond energies (E(HB), kcal mol−1), electron density (ρ, au), and Laplacian of the electron density (∇2ρ, au) for the isolated model of the (001) surface of α-quartz optimized at the M06-2X/6-31G** level
| Bond | H⋯O | O⋯O | ![[double bond splayed right]](https://www.rsc.org/images/entities/char_e00a.gif) O⋯H–O O⋯H–O |
ρ | ∇2ρ | E(HB) |
|---|---|---|---|---|---|---|
| 1 | 1.89 | 2.83 | 162.4 | 0.0275 | 0.0875 | −6.8 |
| 2 | 2.02 | 2.98 | 175.0 | 0.0202 | 0.0613 | −4.3 |
| 3 | 2.02 | 2.99 | 176.0 | 0.0201 | 0.0599 | −4.3 |
| 4 | 1.94 | 2.85 | 154.5 | 0.0248 | 0.0769 | −5.8 |
| 5 | 1.83 | 2.76 | 160.7 | 0.0313 | 0.1033 | −8.3 |
| 6 | 2.32 | 3.25 | 159.7 | 0.0105 | 0.0346 | −1.8 |
| 7 | 1.94 | 2.91 | 178.3 | 0.0238 | 0.0743 | −5.5 |
| 8 | 2.19 | 3.15 | 170.7 | 0.0132 | 0.0422 | −2.4 |
| 9 | 2.12 | 2.94 | 142.1 | 0.0177 | 0.0546 | −3.6 |
| 10 | 1.96 | 2.84 | 149.8 | 0.0244 | 0.0750 | −5.7 |
The structures and AIM data characterizing the hydrogen bonds of the isolated cluster of (001) α-quartz surface and intra-surface H-bonds obtained by the two other methods, namely PBE + D3/6-31G** and PBE + D2/PBC, are presented in the ESI (Table S1).† These approaches basically yield the same results.
Structures of adsorbed systems
Like in the previous section, an AIM analysis has been performed to identify possible hydrogen bonds that are formed during the adsorption of potential contaminants. The geometrical and topological characteristics of the intermolecular hydrogen bonds created during the NCC adsorption are presented in Table 2, Fig. 3–5. The analysis of the optimized geometries of NCC adsorption complexes suggests that the main features of the geometry do not depend on the computational method chosen. Hence, we will discuss the results obtained at the PBE + D2 level using periodic boundary conditions (see Table 2 and Fig. 3).![[double bond splayed right]](https://www.rsc.org/images/entities/char_e00a.gif) X–H⋯Y angles (°), bond energies (E(HB), kcal mol−1), electron density (ρ, au) and Laplacian of the electron density (∇2ρ, au) for the Q(001)⋯TNT(=), Q(001)⋯DNT(=), Q(001)⋯DNAn(=), Q(001)⋯NTO(≥) complexes optimized with various approaches
X–H⋯Y angles (°), bond energies (E(HB), kcal mol−1), electron density (ρ, au) and Laplacian of the electron density (∇2ρ, au) for the Q(001)⋯TNT(=), Q(001)⋯DNT(=), Q(001)⋯DNAn(=), Q(001)⋯NTO(≥) complexes optimized with various approaches
| Bond | Bond type | H⋯Y | X⋯Y | ![[double bond splayed right]](https://www.rsc.org/images/entities/char_e00a.gif) X–H⋯Y X–H⋯Y |
ρ | ∇2ρ | E(HB) |
|---|---|---|---|---|---|---|---|
| PBC using PBE + D2 | |||||||
| Q(001)⋯TNT(=) | |||||||
| HB1 | (N6–)O⋯H–O | 1.83 | 2.79 | 163.8 | 0.0284 | 0.1010 | −7.4 |
| Q(001)⋯DNT(=) | |||||||
| HB1 | (N2–)O⋯H–O | 1.78 | 2.75 | 163.4 | 0.0323 | 0.1150 | −8.9 |
| Q(001)⋯DNAn(=) | |||||||
| — | — | — | — | — | — | — | — |
| Q(001)⋯NTO(≥) | |||||||
| HB1 | N4–H⋯O | 1.77 | 2.77 | 160.4 | 0.0376 | 0.1173 | −10.7 |
| HB2 | (C5–)O⋯H–O | 1.67 | 2.66 | 169.8 | 0.0444 | 0.1472 | −13.9 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Cluster approach, PBE + D3/TZVPPD | |||||||
| Q(001)⋯TNT(=) | |||||||
| – | — | — | — | — | — | — | — |
| Q(001)⋯DNT(=) | |||||||
| HB1 | (N2–)O⋯H–O | 1.89 | 2.86 | 166.3 | 0.0258 | 0.0826 | −6.2 |
| HB2 | (N4)O⋯H–O | 1.80 | 2.75 | 160.2 | 0.0315 | 0.1073 | −8.5 |
| Q(001)⋯DNAn(=) | |||||||
| — | — | — | — | — | — | — | — |
| Q(001)⋯NTO(≥) | |||||||
| HB1 | N4–H⋯O | 1.69 | 2.71 | 164.7 | 0.0451 | 0.1399 | −13.9 |
| HB2 | (C5–)O⋯H–O | 1.73 | 2.72 | 170.7 | 0.0384 | 0.1232 | −11.1 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Cluster approach, M06-2X/6-31G** | |||||||
| Q(001)⋯TNT(=) | |||||||
| — | — | — | — | — | — | — | — |
| Q(001)⋯DNT(=) | |||||||
| HB1 | (N2–)O⋯H–O | 1.90 | 2.87 | 166.0 | 0.0260 | 0.0426 | −5.2 |
| HB2 | (N4)O⋯H–O | 1.82 | 2.77 | 160.4 | 0.0285 | 0.0949 | −7.3 |
| Q(001)⋯DNAn(=) | |||||||
| — | — | — | — | — | — | — | — |
| Q(001)⋯NTO(≥) | |||||||
| HB1 | N4–H⋯O | 1.91 | 2.77 | 140.3 | 0.0279 | 0.0909 | −7.0 |
| HB2 | (C5–)O⋯H–O | 1.93 | 2.78 | 145.3 | 0.0245 | 0.0844 | −5.9 |
| HB3 | N3–O⋯H–O | 2.25 | 2.77 | 112.1 | 0.0145 | 0.0585 | −3.1 |
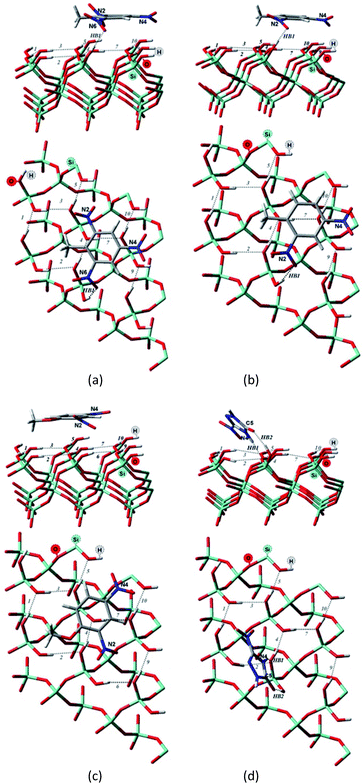 | ||
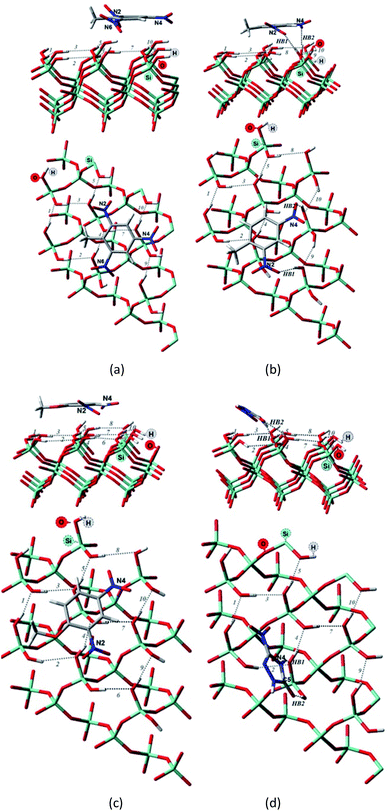
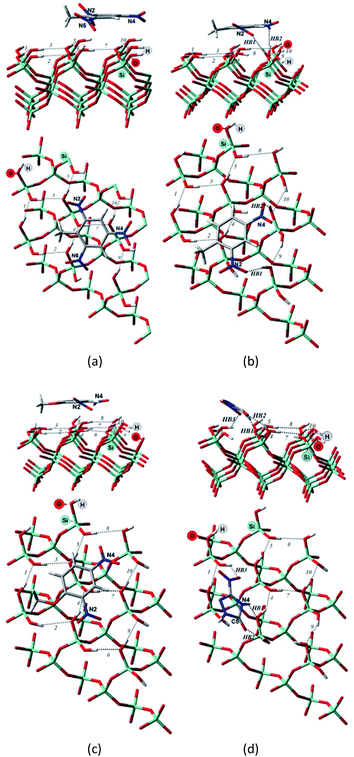
| Fig. 3 Side and top view of the optimized structures of the Q(001)⋯TNT(=) (a), Q(001)⋯DNT(=) (b), Q(001)⋯DNAn(=) (c), Q(001)⋯NTO(≥) (d) adsorption complexes obtained with PBC using PBE + D2. | ||
Although we would have expected the NCCs to establish more hydrogen bonds with the (001) surface because of the lower intra-surface interaction energies of the hydrogen bonds, we identified a considerably smaller number of hydrogen bonds formed compared to the interaction with the (100) surface.25 Only a single hydrogen bond is created due to the adsorption of TNT and DNT with the (001) surface (Table 2, Fig. 3a and b), and two bonds are formed when NTO is adsorbed in a diagonal position (Table 2, Fig. 3d). NTO is different from the other investigated compounds. As it contains a heteroaromatic system, its ketone group and the NH from the ring form two hydrogen bonds with the surface. Overall an eight-membered ring is developed, and the O(C)–(N)H distance (2.8 Å) of the NTO-molecule seemed to be ideal to break into the surface structure: the H(O)–(Si)O distances of the two geminal hydroxyl groups on the surface are close to that value (2.9 Å). DNAn does not exhibit any hydrogen bonds with the surface (Table 2, Fig. 3c). The adsorption of DNAn is thus dominated by electrostatic and dispersion interactions, not by the formation of hydrogen bonds.
Comparing to the geometries obtained with the cluster approach, one less hydrogen bond was computed for TNT (Table 2, Fig. 4a) and additional hydrogen bond was found for the PBE + D3/TZVPPD level structure of DNT (Table 2, Fig. 4b), where both nitro-groups take part in forming two hydrogen bonds, disrupting the surface. Specifically, the 6th and 7th weak hydrogen bonds of the (001) surface (Table 1) point towards the adsorbed molecule, as can be seen in Fig. 4b.
For the M06-2X/6-31G** structures (Table 2, Fig. 5), one additional hydrogen bond is formed for NTO. Note, however, that even though NTO exhibits more hydrogen bonds than the other species, this does not necessarily correlate with the binding energy.
From Fig. 5, we can see that the increased number of hydrogen bonds imply, like mentioned before, a diagonal position of the adsorbed NTO molecule. This results in a decreased value of the dispersion interaction between the molecule and the surface.
Interaction energies of adsorbed systems
The outcomes shown in the Table 3 are similar to the conclusion of the study of the adsorption of investigated compounds on the surface (100).25 We confirm our previous observation that the data became more consistent in case if the contribution from dispersion energies is taken into account by adding D2 and D3 dispersion, even for M06-2X functional. This follows from the comparison of the results obtained at M06-2X level (second column of the Table 3) with the others. Unfortunately, there is no accurate experimental data to compare to. Based on the adsorption energies of silica, oxide and carbon surfaces,25,61–65 we concluded25 that the data obtained at the PBE + D3/TZVPPD level are the best fit to the adsorption energies measured experimentally. In order to compare the results to the ones obtained in our previous publication, we performed single point calculations at the geometry obtained by the M06-2X functional. Table 3 displays the interaction energies of the NNT species for the (001) and (100) surfaces.| Adsorption complex | Method | |||||
|---|---|---|---|---|---|---|
| PBC | Cluster approach | |||||
| GPW (PBE + D2/TZVP) | M06-2X/6-31G** | M06-2X + D3/6-31G** | PBE + D3/6-31G** | PBE + D3/TZVPPD | PBE + D3/TZVPPD//M06-2X/6-31G** | |
| Q(001)⋯TNT(=) | −17.8 | −13.2(−13.8) | −17.5(−18.6) | −17.5(−17.8) | −19.8 | −17.0(−19.4) |
| Q(001)⋯DNT(=) | −14.9 | −13.7(−11.3) | −18.0(−15.6) | −17.1(−16.1) | −20.1 | −17.5(−20.3) |
| Q(001)⋯DNAn(=) | −17.2 | −17.6(−13.7) | −21.5(−18.2) | −17.1(−16.3) | −19.2 | −20.4(−24.4) |
| Q(001)⋯NTO(≥) | −15.2 | −14.1(−19.5) | −16.6(−22.2) | −16.6(−16.6) | −18.2 | −11.8(−25.5) |
The compounds optimized using PBE + D3/TZVPPD are predicted to adsorb on the hydroxylated (001) surface with the order: DNT > TNT > DNAn, while the adsorption energy of NTO is weaker. The reason for the latter is the abovementioned diagonal type of adsorption and a much weaker dispersion interaction for NTO. This contrasts the findings from Table 2, where only the hydrogen bonds were investigated by the AIM analysis, and shows the limitations of the AIM approach. From those tables, we would expect NTO to be bound the strongest.
The large deviation in PBE + D3/TZVPPD//M06-2X/6-31G** from the values obtained applying the other methods can be explained by the observation that M06-2X/6-31G** has vastly different geometries compared to PBE + D3/TZVPPD.
For the (100) surface, the order is almost reversed, with NTO > DNAn > DNT > TNT, indicating that the surface is of vital importance when comparing adsorption energies of the NCCs.
Without D3 dispersion, the adsorption energies of DNT and NTO on the (001) surface are rather similar. We can also see that the inclusion of dispersion is still significant for the M06-2X method, as it increases the adsorption energies by 2–5 kcal mol−1. More importantly, the effects of dispersion are various for different adsorbents, altering their order.
Overall, DNAn, DNT, TNT interact weaker with the (001) than with the (100) surface. For the (100) surface, the adsorption energies are between −25.5 and −19.4 kcal mol−1 at the PBE + D3/TZVPPD//M06-2X/6-31G** level, and for the (001) surface between −20.4 and −11.8 kcal mol−1. We attribute this to the lower amount of hydrogen bonds between the species and (001) surface of hydroxylated silica. The molecule with the lowest adsorption energy (NTO, −11.8 kcal mol−1) is characterized by much larger adsorption energy when PBE + D3/TZVPPD level optimization is performed (−18.2 kcal mol−1).
The pure adsorption energies presented in Table 3 correspond to a temperature of 0 K. Except for DNT, the probably most accurate PBE + D3/TZVPPD cluster values agree well with the PBE + D2 numbers obtained with the mixed plane wave basis set.
The basis set, when going from a double-zeta quality (6-31G**) to a larger TZVPPD basis set, has a smaller, but still important impact, increasing interaction energy from 3.0 kcal mol−1 for DNT to 1.6 kcal mol−1 for the more diagonally bound NTO.
Concerning the functionals, the M06-2X + D3 numbers with the 6-31G** basis set are also comparable to PBE + D3, with the exception of Q(001)⋯DNAn, which shows the largest adsorption energy with this functional. The discrepancy may emerge from the results of Tables 2–4 of the last section: DNAn is the only molecule which does not show any direct hydrogen bonds with the surface. M06-2X is more accurate in describing direct hydrogen bonded contacts than PBE.66,67 However, it overestimates the electrostatic interactions between a molecule and the surface,63 an effect which may lead to the larger value in comparison. Still, it is rather difficult to discuss the accuracy of density functionals for extended system such as surfaces in which hydrogen bonds also play a major role. Like in our previous paper,25 long-range dispersion is important even for the M06-2X functional.
| ΔEads | ΔHads (0 K) | T, °C | ΔGads | ΔHads | TΔSads | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Q(001) | q(100) | Q(001) | q(100) | Q(001) | q(100) | Q(001) | q(100) | Q(001) | q(100) | ||
| TNT | −17.5 | −17.8 | −17.1 | −17.4 | 10 | −3.1 | −0.2 | −17.1 | −17.0 | −13.9 | −16.8 |
| 25 | −2.4 | 0.7 | −17.0 | −17.0 | −14.7 | −17.7 | |||||
| 40 | −1.6 | 1.6 | −17.0 | −17.0 | −15.4 | −18.5 | |||||
| 60 | −0.6 | 2.7 | −17.0 | −17.0 | −16.3 | −19.7 | |||||
| DNT | −17.1 | −16.1 | −16.7 | −15.8 | 10 | −2.3 | −1.3 | −16.7 | −15.2 | −14.4 | −13.9 |
| 25 | −1.5 | −0.5 | −16.7 | −15.2 | −15.2 | −14.7 | |||||
| 40 | −0.8 | 0.2 | −16.6 | −15.1 | −15.9 | −15.3 | |||||
| 60 | 0.3 | 1.1 | −16.6 | −15.1 | −16.9 | −16.2 | |||||
| DNAn | −17.1 | −16.3 | −16.8 | −15.9 | 10 | −1.3 | 0.8 | −16.7 | −15.8 | −15.4 | −16.6 |
| 25 | −0.5 | 1.7 | −16.7 | −15.8 | −16.2 | −17.5 | |||||
| 40 | 0.3 | 2.6 | −16.7 | −15.8 | −17.0 | −18.3 | |||||
| 60 | 1.4 | 3.7 | −16.6 | −15.8 | −18.0 | −19.5 | |||||
| NTO | −16.6(≥) | −16.6 | −15.7 | −16.1 | 10 | −0.3 | −0.3 | −16.1 | −16.2 | −15.8 | −15.9 |
| 25 | 0.5 | 0.5 | −16.1 | −16.2 | −16.6 | −16.7 | |||||
| 40 | 1.4 | 1.4 | −16.2 | −16.2 | −17.6 | −17.6 | |||||
| 60 | 2.5 | 2.5 | −16.2 | −16.2 | −18.7 | −18.7 | |||||
Furthermore, the PBE + D3/TZVPPD values have been recalculated at the M06-2X + D3/6-31G** geometries in order to evaluate the accuracy and difference of the various structures. Interestingly, the obtained values are similar to the M06-2X + D3 ones (with the notable exception that NTO is significantly less bound), which implies that the differences between M06-2X + D3 and PBE + D3 in the adsorption energies can be mainly attributed to the geometries. For both methods, especially the NTO adsorption complex exhibits a very different geometry.
When comparing to the adsorption energies of the (100) surface, the order and energy differences for PBE + D3/TZVPPD//M06-2X + D3/6-31G** are rather similar, with the notable exception of NTO. For the (001) surface it orients only in a diagonal and not parallel position towards the surface, which results in the lower adsorption energy.
More accurate data can be obtained after taking the contribution from the entropic term into account, as done in the next section.
Thermodynamics of adsorption
We used the RRHO approximation to calculate Gibbs free energies (Table 4) with PBE + D3/6-31G** at several environmentally relevant temperatures, namely 10 °C, 25 °C, 40 °C, and 60 °C. The calculated values indicate that the (001) plane is unable to adsorb NTO at larger temperatures due to the positive Gibbs free energies of adsorption. It is also predicted that this plane will not adsorb DNAn at temperatures larger than 40 °C and DNT at temperatures larger than 60 °C.For the (100) α-quartz surface, only DNT adsorbs at lower temperatures than 25 °C, whereas TNT and NTO adsorb at lower temperatures than 10 °C. And while these numbers may be only accurate by ±50 °C because of the methods employed (PBE + D3 with a small basis set, anharmonic effects on zero-point energies and temperature contributions especially in the entropy), a general qualitative trend is observed. TNT is the strongest adsorbate on the (001) surface, followed by DNT on the (001) surface. Then, DNT has the strongest adsorption energy on the (100) surface, together with DNAn on (001). This has some obvious consequences for the isolation of the contaminants on α-quartz as for larger temperatures only TNT and DNT will prevail on the (001) surface.
Subsequently, the data of Table 4 are converted into partition coefficients in Table 5. According to the results, the (001) plane displays an effective adsorption ability regarding TNT, DNT and DNAn. Only NTO is not adsorbed well at the (001) plane at any temperature. At larger temperatures, only TNT is adsorbed on the (001) plane.
| 10 °C | 25 °C | 40 °C | 60 °C | |||||
|---|---|---|---|---|---|---|---|---|
| Q(001) | q(100) | Q(001) | q(100) | Q(001) | q(100) | Q(001) | q(100) | |
| TNT(=) | 3.16 × 102 | 1.449 × 100 | 8.61 × 101 | 2.73 × 10−1 | 1.950 × 101 | 5.13 × 10−2 | 3.05 × 100 | 6.66 × 10−3 |
| DNT(=) | 7.15 × 101 | 1.117 × 101 | 1.619 × 101 | 2.53 × 100 | 4.42 × 100 | 6.89 × 10−1 | 5.73 × 10−1 | 1.298 × 10−1 |
| DNAn(=) | 1.117 × 101 | 2.26 × 10−1 | 2.53 × 100 | 4.26 × 10−2 | 5.73 × 10−1 | 8.01 × 10−3 | 7.44 × 10−2 | 1.040 × 10−3 |
| NTO(≥) | 1.745 × 100 | 1.745 × 100 | 3.95 × 10−1 | 3.95 × 10−1 | 7.43 × 10−2 | 7.43 × 10−2 | 9.65 × 10−3 | 9.65 × 10−3 |
Considering the (100) plane, none of the investigated molecules are well adsorbed at 60 °C, 40 °C and even at lower temperatures, only DNT has good adsorption capability at 10 °C (the partition coefficient is larger than ten).
Summarizing all four nitrocompounds on the two planes of α-quartz at different temperatures: TNT will be mainly adsorbed on (001) surface at any temperature, but will almost not be found on (100) face; DNT will be nearly equally adsorbed on (001) and (100) surfaces; DNAn will be only adsorbed on (001) face; and NTO is not adsorbed well on any of these surfaces.
As data in Table 5 are probably one of the most important outcomes of this study, we can deduce the adsorption of the investigated molecules TNT, DNT, DNAn, and NTO on the most important (001) and (100) α-quartz surfaces. This can provide useful hints related to separation of these species by adsorbing them on quartz surfaces.
Conclusions
This work stresses the importance of investigating several quartz surfaces in order to computationally elucidate the adsorption of larger molecules on silica surfaces, as they yield quite different results.A detailed geometry and energy analysis show a relatively small amount of hydrogen bonds between the investigated nitrocompounds and the (001) surface of α-quartz. The obtained results suggest that for the adsorption on (001) surface, the energy is dominated by the dispersion, while for the (100) surface direct hydrogen bonds play a more crucial role. This also implies that the (100) surface is changing its structure, whereas the (001) surface mainly remains intact when the nitrocompound is adsorbed.
Finally, the analysis of the adsorption thermodynamics (Gibbs free energies, partition coefficients) shed more light on the adsorption ability for (001) and (100) faces of hydroxylated α-quartz at different temperatures. It is concluded that the (001) crystallographic plane has higher adsorption affinity to the considered nitrocompounds than the (100) one.
Conflicts of interest
The authors declare that there is no conflict of interest.Acknowledgements
This work was facilitated by support from the High Performance Computing Distributed Shared Resource Center at the ERDC (Vicksburg, MS) and the Office of Naval Research Grant N00034-03-1-0116. The use of trade, product, or firm names in this report is for descriptive purposes only and does not imply endorsement by the US Government. Results in this study were funded and obtained from research conducted under the Environmental Quality Technology Program of the United States Army Corps of Engineers by the US Army ERDC. Permission was granted by the Chief of Engineers to publish this information. The findings of this report are not to be construed as an official Department of the Army position unless so designated by other authorized documents.Notes and references
- M. Simini, R. S. Wentsel, R. T. Checkai, C. T. Phillips, N. A. Chester, M. A. Majors and J. C. Amos, Environ. Toxicol. Chem., 1995, 14, 623–630 CrossRef CAS.
- G. Dave, E. Nilsson and A.-S. Wernersson, Aquat. Ecosyst. Health Manage., 2000, 3, 291–299 CrossRef CAS.
- J. C. Pennington and J. M. Brannon, Thermochim. Acta, 2002, 384, 291–299 CrossRef.
- S. S. Talmage, D. M. Opresko, C. J. Maxwell, C. J. E. Welsh, F. M. Cretella, P. H. Reno and F. B. Daniel, Rev. Environ. Contam. Toxicol., 1999, 161, 1–156 CrossRef CAS.
- A. B. Crockett, T. F. Jenkins, H. D. Craig and W. E. Sisk, Overview of On-Site Analytical Methods for Explosives in Soil Special Report 98-4, US Army Corps of Engineers Cold Regions Research & Engineering Laboratory, February 1998 Search PubMed.
- M. Kulkarni and A. Chaudhari, J. Environ. Manage., 2007, 85, 496–512 CrossRef CAS PubMed.
- F. W. S. Carver, D. P. Wyndham and T. J. Sinclair, J. Raman Spectrosc., 1985, 16, 332–336 CrossRef CAS.
- F. W. S. Carver and T. S. Sinclair, J. Raman Spectrosc., 1985, 14, 410–414 CrossRef.
- F. C. Hill, L. K. Sviatenko, L. Gorb, S. I. Okovytyy, G. S. Blaustein and J. Leszczynski, Chemosphere, 2012, 88, 635–643 CrossRef CAS.
- O. V. Tinkov, L. N. Ognichenko, V. E. Kuz'min, L. G. Gorb, A. P. Kosinskaya, N. N. Muratov, E. N. Muratov, F. C. Hill and J. Leszczynski, Struct. Chem., 2016, 1, 191–198 CrossRef.
- V. E. Kuz'min, A. G. Artemenko and E. N. Muratov, J. Comput.-Aided Mol. Des., 2008, 22, 403–421 CrossRef.
- H. R. Pouretedal and M. H. Keshavarz, J. Iran. Chem. Soc., 2011, 8, 78–89 CrossRef CAS.
- Y. A. Kholod, E. N. Muratov, L. G. Gorb, F. C. Hill, A. G. Artemenko, V. E. Kuz’min, M. Qasim and J. Leszczynski, Environ. Sci. Technol., 2009, 43, 9208–9215 CrossRef CAS.
- A. Golius, L. Gorb, A. Michalkova Scott, F. C. Hill and J. Leszczynski, Struct. Chem., 2015, 26, 1281–1286 CrossRef CAS.
- L. K. Sviatenko, O. Isayev, L. Gorb, F. C. Hill, D. Leszczynska and J. Leszczynski, J. Comput. Chem., 2015, 36, 1029 CrossRef CAS.
- V. B. Cashin, D. S. Eldridge, A. M. Yu and D. Zhao, Environ. Sci.: Water Res. Technol., 2018, 4, 110–128 RSC.
- A. Michalkova Scott, E. A. Burns and F. C. Hill, J. Mol. Model., 2014, 20, 2373 CrossRef.
- M. K. Shukla and F. Hill, J. Comput. Chem., 2014, 35, 1977–1985 CrossRef CAS.
- A. Michalkova Scott, E. A. Burns, B. J. Lafferty and F. C. Hill, J. Mol. Model., 2015, 21, 21 CrossRef.
- L. K. Sviatenko, L. Gorb, F. C. Hill, D. Leszczynska and J. Leszczynski, J. Phys. Chem. A, 2015, 119, 8139–8145 CrossRef CAS.
- A. Michalkova Scott, L. Gorb, E. A. Mobley, F. C. Hill and J. Leszczynski, Langmuir, 2012, 28, 13307–13317 CrossRef.
- F. Musso, S. Casassa, M. Corno and P. Ugliengo, Struct. Chem., 2017, 28, 1009–1015 CrossRef CAS.
- L. T. Gibson, Chem. Rev., 2014, 43, 5173–5182 CAS.
- N. Jiang, R. Shang, S. G. J. Heijman and L. C. Rietveld, Water Res., 2018, 144, 145–161 CrossRef CAS.
- A. Rimola, D. Costa, M. Sodupe, J.-F. Lambert and P. Ugliengo, Chem. Rev., 2013, 113, 4216–4313 CrossRef CAS.
- O. Tsendra, A. Michalkova Scott, L. Gorb, A. D. Boese, F. C. Hill, M. M. Ilchenko, D. Leszczynska and J. Leszczynski, J. Phys. Chem. C, 2014, 118, 3023–3034 CrossRef CAS.
- M. Svensson, S. Humbel, R. D. J. Froese, T. Matsubara, S. Sieber and K. Morokuma, J. Phys. Chem., 1996, 100, 19357–19363 CrossRef CAS.
- A. D. Boese and J. Sauer, Phys. Chem. Chem. Phys., 2013, 15, 16481–16493 RSC.
- V. V. Murashov, J. Phys. Chem. B, 2005, 109, 4144–4151 CrossRef CAS.
- A. Pedone, G. Malavasi, M. C. Meziani, U. Segra, F. Muss, M. Corno, B. Civalleri and P. Ugliengo, Chem. Mater., 2008, 20, 2522–2531 CrossRef CAS.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS.
- L. Bengtsson, Phys. Rev. B, 1999, 59, 12301 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2008, 4, 1849–1868 CrossRef CAS.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chem. Acc., 1973, 28, 213–222 Search PubMed.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, D. J. DeFrees, J. A. Pople and M. S. Gordon, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef.
- A. Hellweg and D. Rappoport, Phys. Chem. Chem. Phys., 2015, 17, 1010–1017 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel,; G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, et al., Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- R. Ahlrichs, et al., TURBOMOLE, 6.3.1, University of Karlsruhe, 2011, http://www.turbomole-gmbh.com, last accessed 5.9.2019 Search PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, U.K., 1990 Search PubMed.
- F. Biegler-König and J. Schonbohm, J. Comput. Chem., 2002, 23, 1489–1494 CrossRef.
- E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173 CrossRef CAS.
- D. Kosenkov, Y. A. Kholod, L. Gorb, O. V. Shishkin, G. M. Kuramshina, G. I. Dovbeshko and J. Leszczynski, J. Phys. Chem. A, 2009, 113, 9386–9395 CrossRef CAS.
- I. Mata, I. Alkorta, E. Espinosa and E. Molins, Chem. Phys. Lett., 2011, 507, 185–189 CrossRef CAS.
- O. V. Shishkin, L. Gorb and J. Leszczynski, Struct. Chem., 2009, 20, 743–749 CrossRef CAS.
- C. J. Cramer, Essentials of Computational Chemistry-Theory and Models, Wiley, Chichester, 2002 Search PubMed.
- M. K. Kesharwani, B. Brauer and Jan M. L. Martin, J. Phys. Chem. A, 2015, 119, 1701–1714 CrossRef CAS.
- J. Goniakowski and C. Noguera, Surf. Sci., 1994, 319, 68–80 CrossRef CAS.
- F. Musso, P. Mignon, P. Ugliengo and M. Sodupe, Phys. Chem. Chem. Phys., 2012, 14, 10507–10514 RSC.
- F. Musso, M. Sodupe, M. Corno and P. Ugliengo, J. Phys. Chem. C, 2009, 113, 17876–17884 CrossRef CAS.
- A. D. Boese, J. Chem. Theory Comput., 2013, 9, 4403–4413 CrossRef CAS.
- A. Michalkova Scott, L. Gorb, F. Hill and J. Leszczynski, J. Phys. Chem. A, 2011, 115, 2423–2430 CrossRef.
- A. Michalkova Scott, L. Gorb, E. A. Burns, S. N. Yashkin, F. C. Hill and J. Leszczynski, J. Phys. Chem. C, 2014, 118, 4774–4783 CrossRef.
- A. D. Boese and J. Sauer, J. Comput. Chem., 2016, 37, 2374–2385 CrossRef CAS.
- P. Lazar, F. Karlicky, P. Jurecka, M. Kocman, E. Otyepkova, K. Safarova and M. Otyepka, J. Am. Chem. Soc., 2013, 135, 6372–6377 CrossRef CAS.
- A. D. Boese and P. Saalfrank, J. Phys. Chem. C, 2016, 120, 12637–12653 CrossRef CAS.
- A. D. Boese, Mol. Phys., 2015, 14, 1618–1629 CrossRef.
- A. D. Boese, ChemPhysChem, 2015, 140, 978–985 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Structure of (001) α-quartz surface and geometrical characteristics of the O–H⋯O intrasurface H-bonds calculated with different approaches. See DOI: 10.1039/c9ra07130j |
| This journal is © The Royal Society of Chemistry 2019 |