The inverse design of structural color using machine learning†
Abstract
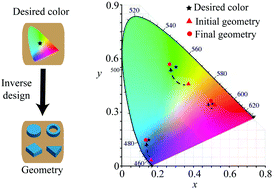
Efficiently identifying optical structures with desired functionalities, referred to as inverse design, can dramatically accelerate the invention of new photonic devices, and this is especially useful in the design of large scale integrated photonic chips. Structural color with high-resolution, high-saturation, and low-loss holds great promise in image display, data storage and information security. However, the inverse design of structural color remains an open challenge, and this impedes practical application. Here, we propose an inverse design strategy for structural color using machine learning (ML) technologies. The supervised learning (SL) models are trained with the geometries and colors of dielectric arrays to capture accurate geometry-color relationships, and these are then applied to a reinforcement learning (RL) algorithm in order to find the optical structural geometries for the desired color. Our work succeeds in finding simple and accurate models to describe geometry-color relationships, which significantly improves the efficiency of the design. This strategy provides a systematic method to directly encode generic functionality into a set of structures and geometries, paving the way for the inverse design of functional photonic devices.


 Please wait while we load your content...
Please wait while we load your content...