Bond valences and anharmonicity in vacancy-ordered double perovskite halides†
Abstract
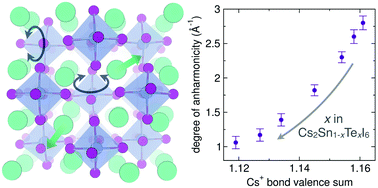
Anharmonic lattice dynamics are intimately linked with optical and electronic properties in perovskite halide semiconductors. Vacancy-ordered double perovskites are a subset of the perovskite halide family containing isolated octahedral units. The absence of polyhedral connectivity engenders the vacancy-ordered double perovskites with additional degrees of dynamic freedom, which presents an ideal structural framework to study dynamic–property relationships in perovskite halide semiconductors. In the present study, we examine the structure and bonding origins of anharmonicity in the vacancy-ordered double perovskites Cs2Sn1−xTexI6. While X-ray diffraction indicates that all members adopt the cubic vacancy-ordered double perovskite structure, the local coordination environment probed by X-ray pair distribution function (XPDF) analysis reveals asymmetry of the Cs–I/I–I pair correlation that smoothly decreases with increasing tellurium content. Temperature-dependent neutron total scattering suggests that this asymmetry in the PDF occurs due to anharmonic lattice dynamics arising from octahedral tilting and Cs+ displacements, as supported by Reverse Monte Carlo simulations of the Cs2SnI6 and Cs2TeI6 end members. We further correlate the trends in asymmetry and anharmonicity with the bond valence sum of the Cs+ ion, and find that the anharmonicity vanishes when the bonding preferences of the Cs+ are satisfied by the size of the cuboctahedral void. This study presents a simple and effective approach for understanding the origin of anharmonicity in vacancy-ordered double perovskite materials.
- This article is part of the themed collection: Journal of Materials Chemistry C Emerging Investigators


 Please wait while we load your content...
Please wait while we load your content...