Phase polymorphism and electronic structures of TeSe2†
Abstract
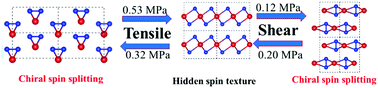
Structure prediction complemented by density functional theory (DFT) calculation indicates that TeSe2 is the most stable among the various Te(1−x)Sex compounds. Different from the case of bulk Te, the material can equally adopt three different crystal structures: HγT, MH, and Mβα phases, which are similar to 1T-TiSe2, trigonal Te, and orthorhombic Te, respectively. These phases can be transformed from one to another by uniaxial tensile and shear stress of less than 1 MPa; they can be even transformed to their chiral mirror images. Band structure calculations including spin–orbit coupling (SOC) show that all three phases are semiconductors. The band gap (= 0.43 eV) increases with density, being the largest (= 1.86 eV) in the Mβα phase with the highest density. The HγT phase exhibits a hidden spin texture because of centrosymmetry. The other two phases display chiral spin texture due to the lack of symmetry, in that two spin components of frontier bands can split by more than 100 meV in opposite directions.


 Please wait while we load your content...
Please wait while we load your content...