Recent developments in photonic, plasmonic and hybrid nanowire waveguides
Abstract
Recent years have seen a rapid expansion of research into photonic and plasmonic nanowire waveguides for both fundamental studies and technological applications, because of their ability to propagate and process optical signals in tightly confined light fields with high speed and low power, space and material requirements. This comprehensive review summarizes recent advances in the fabrication, characterization and applications of both photonic and plasmonic NW waveguides, with a special focus on the comparative discussion of their differences and similarities in mechanisms and properties, strengths and limitations in performance, and how they can work together in hybrid devices with performances and applications that neither can achieve individually. We also provide an outlook on the future opportunities and directions in this exciting field.
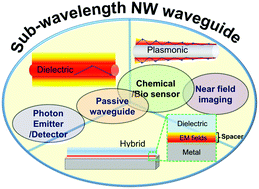
- This article is part of the themed collections: Recent Review Articles, Photonics and Journal of Materials Chemistry C Emerging Investigators


 Please wait while we load your content...
Please wait while we load your content...