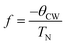Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Magnetic ordering in a frustrated bow-tie lattice†
Laura J.
Vera Stimpson
 a,
Efrain E.
Rodriguez
a,
Efrain E.
Rodriguez
 b,
Craig M.
Brown
b,
Craig M.
Brown
 c,
Gavin B. G.
Stenning
d,
Marek
Jura
c,
Gavin B. G.
Stenning
d,
Marek
Jura
 d and
Donna C.
Arnold
d and
Donna C.
Arnold
 *a
*a
aSchool of Physical Sciences, University of Kent, Canterbury, Kent, CT2 7NH, UK. E-mail: d.c.arnold@kent.ac.uk; Tel: +44 (0)1227 827810
bDepartment of Chemistry and Biochemistry, University of Maryland, College Park, Maryland 20742-2115, USA
cNIST Center for Neutron Research, 100 Bureau Drive, Gaithersburg, Maryland 20899-8562, USA
dISIS Neutron and Muon Source, Rutherford Appleton Laboratory, Harwell Science and Innovation Campus, Didcot, OX11 0QX, UK
First published on 17th April 2018
Abstract
We report a systematic X-ray and powder neutron diffraction study of the geometrically frustrated material, Ca2Mn3O8. Ca2Mn3O8 exhibits a ‘bow-tie’ like connectivity of Mn4+ with Ca2+ occupying octahedral sites between MnO6 layers. Magnetic refinements of neutron powder diffraction data indicate that the spins order with a canted four sub-lattice-like (↑↑↓↓) arrangement below ∼50 K. In addition, short range magnetic correlations can be seen to persist until ∼130 K.
Introduction
Geometric frustration arises when interactions between magnetic degrees of freedom are incompatible with the underlying crystal geometry.1 In materials which exhibit triangular (e.g. delafossite2 and kagomé3), tetrahedral (e.g. pyrochlore4), honeycomb (e.g. Bi3Mn4O12NO35) and ‘bow-tie’ connectivity between magnetic species each spin cannot satisfy all pairwise interactions leading to ground state degeneracy and the realization of unconventional magnetic properties.6 In systems with Jahn–Teller (JT) active species the magnetic spin alignment can also result in an ordered arrangement of the JT distorted MO6 octahedral bond arrangement resulting in the emergence of weak ferroelectric character.Layered transition metal oxides are emerging as an important class of frustrated materials due to their compositional flexibility and wide range of applications. In these materials frustration can be (partially) lifted through either the propagation of a 120° spin spiral or incommensurate spin order through lattice distortions leading to a wide range of exotic magnetic states.2,7–10 For example, CuFeO2 has been shown to exhibit two magnetic phase transitions the first at ∼14 K and a second at ∼11 K. At 14 K the material exhibits a collinear spin density wave with an incommensurate modulation which turns into collinear commensurate four sub-lattice (4SL, ↑↑↓↓) ordering at TN (11 K).2 In contrast, incorporation of Jahn–Teller active Mn3+ ions into CuMnO2 results in complex nearest neighbour, J1 and diagonal nearest neighbour, J2 interactions which lead to a frustrated square lattice due to an anisotropy of the triangular lattice.10 This results in magnetic spins which are antiferromagnetically (AFM) aligned along the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] direction and ferromagnetically aligned along the [110] direction corresponding to a collinear AFM order.10
0] direction and ferromagnetically aligned along the [110] direction corresponding to a collinear AFM order.10
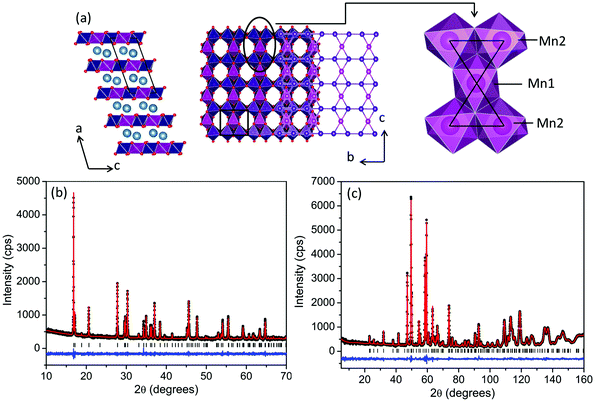
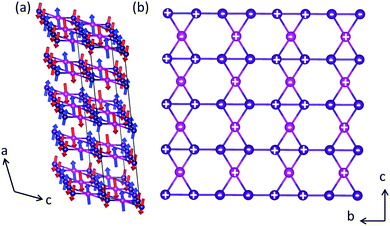
The layered transition metal oxide, Ca2Mn3O8, is beginning to attract attention within the literature. This material can be thought of as comprising of a series of MnO6 layers separated, by Ca2+ ions. However, in contrast with the triangular layered transition metal oxides, both the A-cation and B-cation layers can be thought of as incomplete (nominal formula Ca0.5Mn0.75O2) resulting in an ordered vacancy within the layers similar to that seen in kagomé lattices. However, in contrast with kagomé lattices, where the vacancy is ordered in a staggered diagonal fashion, the vacancy in Ca2Mn3O8 is ordered in a striped arrangement realizing a ‘bow-tie’ connectivity of the Mn sub-lattice and a potentially frustrated geometry (Fig. 1). The location of this vacancy alternates between subsequent MnO6 layers giving rise to ABAB stacking with the Ca2+ occupying octahedral co-ordination within the layers. Research into Ca2Mn3O8 has been primarily focused on its catalytic and electrochemical characteristics with the magnetic properties largely ignored since the first structural reports in the 1980's.11–16 Recently we investigated the effects of morphology on the magnetic properties of Ca2Mn3O8 based on the synthetic methods reported in the literature.17 We demonstrated that it could be expected that Ca2Mn3O8 materials would exhibit more complex antiferromagnetic spin order than a simple ↑↓ spin arrangement.17 We also noted that the quality of materials produced by these methods limited any detailed magnetic studies.17 The magnetic behaviour of the isostructural material, Mn2Mn3O8 (Mn5O8) has also recently been reported by Kishore et al.18 They proposed four different magnetic spin arrangements and generated simulated patterns which they then compared to powder neutron diffraction data collected at 9 K.18 Subsequently, they differentiate between their assumed models using ab initio total energy calculations which suggested a model where both the MnO6 layers and Mn2+ interlayer ions are coupled antiferromagnetically with all the spins located around the manganese ‘bow-tie’ coupled ferromagnetically to be the lowest energy.18 We note, however, that these materials were synthesised using a wet chemical route (similar to our previous studies on Ca2Mn3O817) with the resulting materials poorly crystalline potentially leading to difficulties fully identifying the magnetic structure experimentally.18
In this paper we report the first synthesis of high quality bulk Ca2Mn3O8, allowing us to perform a systematic structural and magnetic study of a material with a ‘bow-tie’ lattice. A 4SL-like (↑↑↓↓) ordering is clearly indexed from the magnetic Bragg structure with short range magnetic correlations persisting above TN.
Experimental
Single phase polycrystalline Ca2Mn3O8 was prepared using molten salt synthesis methods similar to those reported previously for Hollandite materials.19 Stoichiometric ratios of CaCO3 and MnCO3 (both Sigma Aldrich, ≥99.0%) were mixed with a 350% (w/w) eutectic mixture of KCl/NaCl and reacted at 700 °C (ramp rate 10 °C min−1) for 48 hours after which the sample was quenched to room temperature. The material was then washed and dried at ambient temperature. An additional 350% (w/w) eutectic mixture of KCl/NaCl was added and the mixture further heated at 700 °C (ramp rate 10 °C min−1) for an additional 24 hours and quenched to room temperature.Phase purity was initially determined using a Bruker D8 Advance powder diffractometer over a 2θ range of 10° to 70° (40 kV and 40 mA, with λ = 1.54413 Å). Subsequent high quality and variable temperature data was collected between 12 K and 300 K using a Rigaku SmartLab rotating Anode θ/2θ instrument over a 2θ range of 10° to 70° (45 kV and 200 mA, with λ = 1.54413 Å). Neutron Powder Diffraction (NPD) data were collected using the BT-1 32 detector neutron powder diffractometer at the NIST Center for Neutron Research (NCNR). The sample was loaded into a vanadium can of length 50 mm and diameter 10.8 mm. Data were collected at several temperatures between 4 K and 300 K. A Ge(311) monochromator with a 75° take-off angle, λ = 2.0787(2) Å, and in-pile collimation of 60′ were used. Data were collected over the range of 1.3°–166.3° 2θ with a step size of 0.05°. Inelastic neutron diffraction data was collected between 4 K and 150 K using the Disc Chopper Spectrometer (DCS) at the NCNR. Data were collected with a chopper speed of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm and a graphite filter at wavelengths of 1.8 Å and 2.5 Å using the same sample environment (vanadium can) as for the BT-1 experiments.
000 rpm and a graphite filter at wavelengths of 1.8 Å and 2.5 Å using the same sample environment (vanadium can) as for the BT-1 experiments.
Magnetic susceptibility data were collected at the Materials Characterisation Laboratory at the ISIS Neutron and Muon facility using a Magnetic Property Measurement System (MPMS) XL-7 instrument. Zero-field cooled/field cooled data were collected in a temperature range of 2 K to 300 K with an applied magnetic field (H) of 0.1 T. Field dependence hysteresis measurements were performed at 2 K, 25 K and 300 K between ±7 T. AC susceptibility measurements were performed using the Quantum design PPMS-9 Physical Property Measurements System. Data were collected as a function of frequency between 100 Hz and 2700 Hz over a temperature range of 2 K to 100 K.
[Certain commercial equipment, instruments, or materials are identified in this document. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology nor does it imply that the products identified are necessarily the best available for the purpose.]
Results and discussion
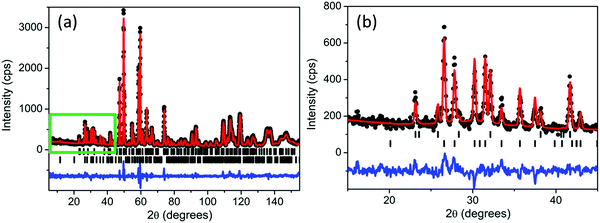
Room temperature diffraction data clearly demonstrated the formation of single phase Ca2Mn3O8 with no indication of either Mn2O3 or CaMnO3 impurities. Refinements performed using the GSAS suite of programs20,21 indicated excellent agreement to the monoclinic, C2/m, model proposed by Ansell et al.11 The Rietveld refinement profile for both room temperature powder neutron and X-ray diffraction data are shown in Fig. 1 with parameter details given in Table 1. All refinement details are given in the ESI.† Bond-valence analysis was performed on the neutron diffraction data collected at 300 K using the VaList program in order to probe the oxidation state of the manganese.22 This gives bond valences of 4.0(1) and 3.9(2) on the Mn1 and Mn2 crystallographic sites respectively consistent with the expected Mn oxidation state of 4+.| Parameter | X-ray | Neutron |
|---|---|---|
| χ 2 | 0.9383 | 0.9822 |
| wRp (%) | 4.98 | 4.52 |
| R p (%) | 3.90 | 3.69 |
| a (Å) | 11.0131(1) | 11.023(2) |
| b (Å) | 5.84160(9) | 5.84629(8) |
| c (Å) | 4.93926(8) | 4.94346(7) |
| β (°) | 109.78(1) | 109.771(1) |
| Cell vol. (Å3) | 299.016(5) | 299.785(6) |
| Ca (x, 0, y) | 0.7244(3) | 0.7248(3) |
| 0.6656(1) | 0.6661(5) | |
| Ca U(iso)/U(e) × 100 (Å2) | 1.00 | 0.4(1) |
| Mn1 (0, 0, ½) | — | — |
| Mn1 U(iso)/U(e) × 100 (Å2) | 1.00 | 1.3(2) |
| Mn2 (0, y, 0) | 0.2575(1) | 0.2577(6) |
| Mn2 U(iso)/U(e) × 100 (Å2) | 1.00 | 0.7(1) |
| O1 (x, y, z) | 0.1004(2) | 0.1005(2) |
| 0.2296(2) | 0.2228(3) | |
| 0.3982(2) | 0.3919(3) | |
| O1 U(iso)/U(e) × 100 (Å2) | 1.00 | 0.66(7) |
| O2 (x, ½, z) | 0.5913(2) | 0.5967(2) |
| 0.8886(1) | 0.9011(4) | |
| O2 U(iso)/U(e) × 100 (Å2) | 1.00 | 0.52(9) |
| O3 (x, 0, z) | 0.5984(2) | 0.6041(3) |
| 0.9609(3) | 0.9605(4) | |
| O3 U(iso)/U(e) × 100 (Å2) | 1.00 | 1.0(1) |
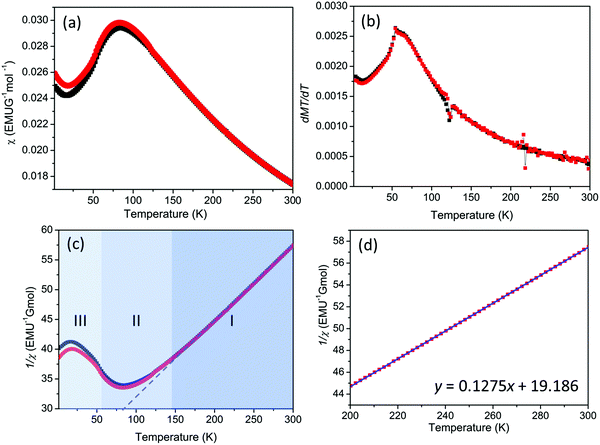
DC magnetic susceptibility data indicates a broad peak with a maximum at approximately 80 K consistent with low dimensional/frustrated antiferromagnetic ordering (Fig. 2).23 The derivative dχT/dT clearly demonstrates that TN = 58 K (Fig. 2 and ESI†). Examination of the Curie–Weiss behaviour indicates a deviation from linearity at approximately 130 K (T*) (Fig. 2). These deviations are common in frustrated systems and suggest that whilst magnetic correlations are building up as the material is cooled, frustration acts to hinder the formation of a three dimensional (Néel) ordered state.24 An effective magnetic moment, μeff, was calculated at 300 K to be 6.47 μB per formula unit consistent with that expected for Mn4+ (μcalc = 6.7 μB per formula unit) in Ca2Mn3O8 consistent with our previous study.17 The Weiss constant, θCW, was determined to have a value of −150.5 K. The level of frustration in the material can be determined using the frustration index, f, as given by;25,26
This gives a frustration index of approximately 2.6 confirming some level of frustration in this material; a frustration index value of 1 would normally be expected for non-frustrated spin order.27 To put this into context, in related layered triangular lattices frustration indexes as low as 1.3 and as high as 13 have been reported.19,28,29 It should be noted, however, that care needs to be taken when making direct comparisons of f or using it explicitly as evidence of frustration since it is greatly influenced by nearest neighbour interactions and dimensionality.24 Slight deviations between the zero field cooled and field cooled data are evident below TN suggesting the possibility of weak ferromagnetic interactions or spin glass-like behaviour. However, as with our previous study, there is no evidence of either appreciable field or frequency dependence of the susceptibility as a function of temperature as shown in Fig. S7 and S8 in the ESI† which would seem to rule out these possibilities (ESI†).17
Variable temperature X-ray (XRD) and neutron diffraction studies were performed in order to further understand the temperature dependence and magnetic ordering in this material. Refinement of these data demonstrated the material could be satisfactorily indexed to the C2/m model with no obvious change in symmetry over the whole temperature range studied (12–300 K). Rietveld refinement details and profiles are shown in the ESI.†
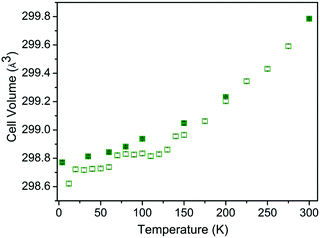
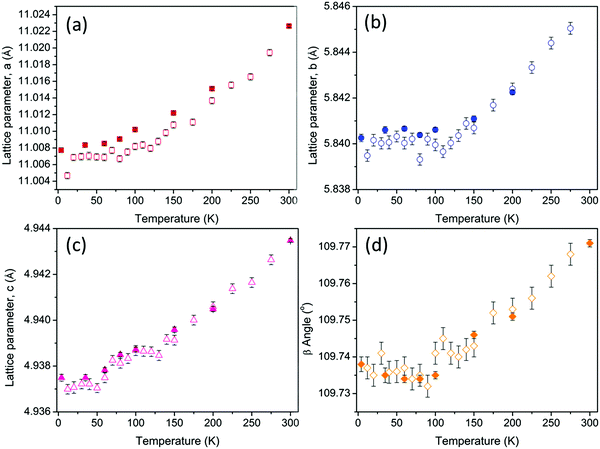
The temperature dependence of the cell volume shows thermal expansion above approximately 50 K as expected for layered metal oxide materials. However, this expansion clearly demonstrates two distinct regions with different slopes which intersect at approximately 130 K (Fig. 3). The temperature dependence of the lattice parameters is even less straight forward. The a and c parameters exhibit linear thermal expansion above 50 K as shown in Fig. 4. In contrast both the b parameter and the β angle exhibit invariant behaviour up to approximately 130 K (Fig. 4) giving rise to the behaviour observed in the cell volume. This temperature is consistent with the deviation from Curie–Weiss behaviour at T* and may suggest the possibility of low dimensional spin ordering or correlations in the lattice b direction which do not result in the formation of 3-dimensionally ordered Néel state between TN and T*.
Close inspection of the powder neutron diffraction data clearly indicates the presence of magnetic Bragg peaks in the 35 K and 4 K data consistent with long range magnetic order below TN. The magnetic structure was determined using SARAh30,31 and the Fullprof32,33 suite and programs. The magnetic Bragg peaks, evident below TN, can be indexed with a commensurate propagation vector k = ½a* + ½b* or (½, ½, 0) using the k-search routine in Fullprof. Essentially, this vector doubles the chemical unit cell in the a- and b-directions to make the magnetic unit cell. From the parent space group C2/m and propagation vector k, we found the little group Gk, which contains only two symmetry elements—the identity operation and inversion centre. Within Gk, there are two irreducible representations, Γ1 and Γ2, which are one-dimensional. Table S6 (ESI†) lists the basis vectors for both Γ1 and Γ2 with respect to both the Mn1 and Mn2 crystallographically distinct sites. Essentially, Γ1 is the totally symmetric representation that couples all the equivalent positions within the Mn1 and Mn2 sites ferromagnetically. For the Mn2 site, Γ2 couples the atoms at x, y, z and −x, −y, −z antiferromagnetically. We found the best solution to be one where Γ1 describes the Mn1 and Γ2 describes Mn2 sites respectively with the two sites anticoupled to each other. After fitting the magnetic Bragg peaks with this model, we obtained goodness-of-fit parameters χ2 = 1.21, Rp = 11.1%, Rwp = 11.7 and magnetic R factor = 12.99% as shown in Fig. 5. Furthermore, the magnetic structure can be described as belonging to the magnetic space group PS![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) . Goodness-of-fit parameters for 35 K are detailed in Table S5 (ESI†) with the refinement profile given in Fig. S5 (ESI†). The components of the moments were observed to be 2.5(2) μB and 2.0(2) μB on the Mn1 and Mn2 sites respectively at 4 K. However, whilst the moments on the Mn1 site lie exclusively along the crystallographic a direction, the spins on the Mn2 crystallographic site exhibit an additional cant in the c-direction with moments of 2.1(2) μB and 0.57(5) μB in the a- and c-directions respectively. Attempts to refine the moments of the Mn1 site in the c-direction resulted in unstable refinements whilst refining both the Mn1 and Mn2 moments in the b-direction resulted in values of zero within reported errors. We also note that whilst the Mn1 crystallographic site is reasonably close to the 3 μB expected for S = 1.5, the observed moment on the Mn2 crystallographic site is lower than expected suggesting that full static order of the moments is not achieved at 4 K. The full magnetic spin structure is shown in Fig. 6. The spin structure can be described by staggered single ferromagnetic stripes that run parallel to the c-direction. This results in a canted 4SL-like ↑↑↓↓ spin arrangement along the base of the ‘bow-ties’ in the b-direction with these spins canted in the c-direction. The centre of the ‘bow-ties’ are coupled antiferromagnetically in the c-direction and act like pinning centres such that the moment lies solely in the a-direction. Between the MnO6 layers the spins are coupled antiferromagnetically in the a-direction and ferromagnetically in the (110) plane. This is in contrast with the structure reported for Mn2Mn3O8 whereby the spin order within the MnO6 layers (and thus around the ‘bow-tie’) is ferromagnetic but the coupling between layers is antiferromagnetic.18 Refinement of the data collected at 35 K further confirms the proposed magnetic structure with no obvious changes in magnetic symmetry as a function of temperature. Considering the alternative model, whereby the magnetic spins are now angled in the bc plane, provides a significantly worse magnetic R factor (magnetic R factor = 192.5%) and clearly fails to model the observed magnetic Bragg peaks as shown in Fig. S6 in the ESI† further confirming the robustness of the Γ1, Γ2 solution proposed above (†).
. Goodness-of-fit parameters for 35 K are detailed in Table S5 (ESI†) with the refinement profile given in Fig. S5 (ESI†). The components of the moments were observed to be 2.5(2) μB and 2.0(2) μB on the Mn1 and Mn2 sites respectively at 4 K. However, whilst the moments on the Mn1 site lie exclusively along the crystallographic a direction, the spins on the Mn2 crystallographic site exhibit an additional cant in the c-direction with moments of 2.1(2) μB and 0.57(5) μB in the a- and c-directions respectively. Attempts to refine the moments of the Mn1 site in the c-direction resulted in unstable refinements whilst refining both the Mn1 and Mn2 moments in the b-direction resulted in values of zero within reported errors. We also note that whilst the Mn1 crystallographic site is reasonably close to the 3 μB expected for S = 1.5, the observed moment on the Mn2 crystallographic site is lower than expected suggesting that full static order of the moments is not achieved at 4 K. The full magnetic spin structure is shown in Fig. 6. The spin structure can be described by staggered single ferromagnetic stripes that run parallel to the c-direction. This results in a canted 4SL-like ↑↑↓↓ spin arrangement along the base of the ‘bow-ties’ in the b-direction with these spins canted in the c-direction. The centre of the ‘bow-ties’ are coupled antiferromagnetically in the c-direction and act like pinning centres such that the moment lies solely in the a-direction. Between the MnO6 layers the spins are coupled antiferromagnetically in the a-direction and ferromagnetically in the (110) plane. This is in contrast with the structure reported for Mn2Mn3O8 whereby the spin order within the MnO6 layers (and thus around the ‘bow-tie’) is ferromagnetic but the coupling between layers is antiferromagnetic.18 Refinement of the data collected at 35 K further confirms the proposed magnetic structure with no obvious changes in magnetic symmetry as a function of temperature. Considering the alternative model, whereby the magnetic spins are now angled in the bc plane, provides a significantly worse magnetic R factor (magnetic R factor = 192.5%) and clearly fails to model the observed magnetic Bragg peaks as shown in Fig. S6 in the ESI† further confirming the robustness of the Γ1, Γ2 solution proposed above (†).
Previously Warren demonstrated that low dimensional order could be characterised by diffuse anisotropic reflections which exhibit a sharp rise at low Q with a slow fall off at higher Q (Q = 2π/d).34 In related layered materials, such as α-NaMnO2, the presence of Warren peaks has been used to describe two-dimensional short range spin order within the metal oxide layers above TN and below T*.23,24 However, we find no evidence of strong Warren peaks within our data suggesting that 2D ordering of the spins within the MnO6 layers above TN and below T* does not occur. Alternatively if we consider the possibility of the formation of spin-ordered 1D chains in the crystallographic b direction, consistent with the observed invariant effect, a sharper step-like feature in the background would be expected to be observed.23,35 We note that above TN we see a broad anisotropic deviation in the background which propagates over a 2θ range of approximately 20°–40° rather than the sharper features expected from 1D ordering (Fig. 7). This behaviour shows a clear temperature dependence which indicates that it is most likely magnetic in origin. With decreasing temperature below T* this deviation increases in intensity up to ∼60 K before abruptly disappearing at TN with the onset of the magnetically ordered state, with only a weak deviation in the background remaining. This behaviour may suggest a transition from a magnetically correlated to a fully ordered state at TN. However, given the energy range that the diffraction data is integrated over it is difficult to determine if this behaviour arises as a result of 2D or 1D static interactions in the elastic channel or dynamic correlations in the inelastic channel.
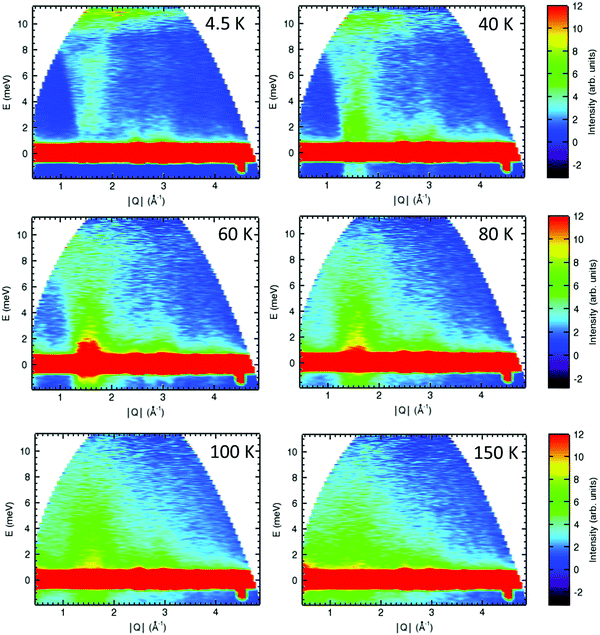
Preliminary inelastic scattering (INS) experiments were performed using the Disc Chopper Spectrometer (DCS) at the NIST centre for neutron research to further investigate the spin dynamics of Ca2Mn3O8 to understand if the missing magnetic moment is dynamic and thus only in the inelastic channel. In order to investigate the anomalous background behaviour observed in the diffraction data we took an energy cut (−1 to 1 meV) across the whole Q-range. This allows purely for the analysis of the elastic range of the spectrum. There is no evidence of anisotropic Warren-like and/or 1D step-like behaviour across all temperatures studied (ESI,† Fig. S10). Since these contributions are elastic in nature this confirms that deviations in the background observed in the diffraction data arise as a result of inelastic interactions as opposed to low-dimensional ordering of static-correlations as have been reported for α-NaMnO26,23 and AgCrS228 materials. The spectra collected at λ = 2.5 Å show a clear temperature dependence with inelastic scattering observed in a Q range of approximately 1.4 Å to 2.0 Å consistent with the Q range of the observed magnetic Bragg peaks in the elastic channel (Fig. 8). At 4 K this scattering is fairly weak in nature consistent with the formation of a three-dimensional ordered Néel state. As the temperature approaches TN these features of the spectrum become more intense consistent with the loss of magnetic order and increased dynamic motion of the spins. Above TN there is a clear band of intensity which extends to approximately 3 meV. This band of intensity becomes more diffuse and less well defined with increasing temperature before collapsing completely between 100 K and 150 K consistent with T*. These data suggest that even below TN the spins still retain some dynamic motion, particularly those on the crystallographic Mn2 site as evidenced by the lower than expected magnetic moment associated with this site in the crystallographic data and the observed spin canting of the Mn2 site. This may act to relieve frustration in the lattice and we are currently in the process of collecting additional INS data and modelling/fitting these data further which will be reported in a subsequent manuscript.
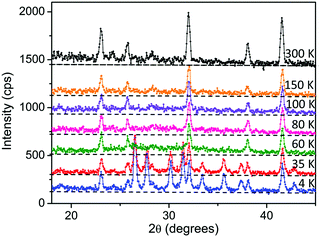 | ||
| Fig. 7 Neutron diffraction data collected for Ca2Mn3O8 showing the temperature dependence of the deviations/Warren-like behaviour of the background. Note the dotted line is a guide for the eye. | ||
Conclusions
In summary the magnetic behaviour of Ca2Mn3O8 is clearly complex. Two transitions, TN and T*, occur at approximately 58 K and 130 K respectively. Below T* short range spin correlations are observed. These are clearly linked to the crystallographic b-direction but fully ordered 1D chains are not realized. At TN a three-dimensional ordered Néel state is observed. Frustration results in quasi-static behaviour of the spins on the Mn2 site such that frustration is partially relieved through the adoption of a dynamic spin state. However, the pinning centres provided by the Mn1 site act to stabilize the material and prevent the formation of wholly dynamic (spin-liquid) state. Clearly the ‘bow-tie’ lattice offers an exciting platform for complex magnetic order and further investigations are necessary to fully understand these phenomena.Conflicts of interest
We report no conflicts of interests.Acknowledgements
This work has been supported through the award of an EPSRC DTA studentship (LJV). DCA is grateful for Guest Researcher Fellowships at the NIST Centre for Neutron Research (NCNR) 2014, 2015. We are also grateful for access to the Materials Characterization laboratories at the ISIS Neutron and Muon Source.Notes and references
- R. Moessner and A. P. Ramirez, Phys. Today, 2006, 59, 24 CrossRef CAS.
- N. Terada, D. D. Khalyavin, P. Manuel, T. Osakabe, P. G. Radaelli and H. Kitazawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 220403 CrossRef.
- J. L. Atwood, Nature, 2002, 294, 1495 Search PubMed.
- S. T. Bramwell and M. J. P. Gingras, Science, 2001, 1, 91 Search PubMed.
- M. Matsuda, M. Azuma, M. Tokunaga, Y. Shimakawa and N. Kumada, Phys. Rev. Lett., 2010, 105, 187201 CrossRef CAS PubMed.
- C. Stock, L. C. Chapon, O. Adamopoulos, A. Lappas, M. Giot, J. W. Taylor, M. A. Green, C. M. Brown and P. G. Radaelli, Phys. Rev. Lett., 2009, 103, 077202 CrossRef CAS PubMed.
- A. M. Abakumov, A. A. Tsirlin, I. Bakaimi, G. Van Tendeloo and A. Lappas, Chem. Mater., 2014, 26, 3306 CrossRef CAS.
- C. Vecchini, M. Poienar, F. Damay, O. Adamopoulos, A. Daoud-Aladine, A. Lappas, J. M. Perez-Mato, L. C. Chapon and C. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094404 CrossRef.
- N. Terada, Y. Tsuchiya, H. Kitazawa, T. Osakabe, N. Metoki, N. Igawa and K. Ohoyama, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 064432 CrossRef.
- F. Damay, M. Poienar, C. Martin, A. Maignan, J. Rodriquez-Carvajal, G. Andre and J. P. Doumerc, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 094410 CrossRef.
- G. B. Ansell, M. A. Modrick, J. M. Longo, K. R. Poeppelmeier and H. S. Horowitz, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1982, 28, 1795 CrossRef.
- H. S. Horowitz and J. M. Longo, Inorg. Chem., 1983, 22, 73 CAS.
- T. R. White, W. S. Glaunsinger, H. S. Horowitz and J. M. Longo, J. Solid State Chem., 1979, 29, 205 CrossRef CAS.
- Y. J. Park and M. A. Doeff, Solid State Ionics, 2006, 177, 893 CrossRef CAS.
- X. Han, T. Zhang, J. Du, F. Cheng and J. Chen, Chem. Sci., 2013, 4, 368 RSC.
- M. M. Najafpour and N. Pashaei, Dalton Trans., 2012, 41, 4799 RSC.
- L. J. Vera Stimpson, S. Ramos, G. B. G. Stenning, M. Jura, S. Parry, G. Cibin and D. C. Arnold, Dalton Trans., 2017, 46, 14130 RSC.
- M. R. A. Kishore, H. Okamoto, L. Patra, R. Vidya, A. O. Sjastad, H. Fjellvag and P. Ravindran, Phys. Chem. Chem. Phys., 2016, 18, 27885 RSC.
- A. M. Larson, P. Moetakef, K. Gaskell, C. M. Brown, G. King and E. E. Rodriguez, Chem. Mater., 2015, 27, 515 CrossRef CAS.
- A. C. Larson and R. B. von Dreele, Los Alamos Natl. Lab., 1994, 96, 86 Search PubMed.
- B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210 CrossRef CAS.
- A. S. Wills, VaList v.4.0.7, 1998, http://www.ccp14.ac.uk Search PubMed.
- M. Giot, L. C. Chapon, J. Androulakis, M. A. Green, P. G. Radaelli and A. Lappas, Phys. Rev. Lett., 2007, 99, 247211 CrossRef PubMed.
- A. S. Wills, N. P. Raju, C. Morin and J. E. Greedan, Chem. Mater., 1999, 11, 1936 CrossRef CAS.
- J. P. Attfield, Chem. Mater., 1998, 10, 3239 CrossRef CAS.
- A. P. Ramirez, Annu. Rev. Mater. Sci., 1994, 24, 453 CrossRef CAS.
- C. Yin, G. Li, W. A. Kockelmann, F. Liao, J. P. Atfield and J. Lin, Chem. Mater., 2010, 22, 3269 CrossRef CAS.
- F. Damay, C. Martin, V. Hardy, G. Andre, S. Petit and A. Maignan, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 184413 CrossRef.
- D. Billington, D. Ernstring, T. E. Millichamp, C. Lester, S. B. Dugdale, D. Kersh, J. A. Duffy, S. R. Giblin, J. W. Taylor, P. Manuel, D. D. Khalyavin and H. Takatsu, Sci. Rep., 2015, 5, 12428 CrossRef PubMed.
- A. S. Wills, Physica B, 2000, 276, 680 CrossRef.
- A. S. Wills, Z. Kristallogr, Suppl., 2009, 30, 39 CrossRef.
- J. Rodriguez-Carvajal, Fullprof Version 2.05, 2011, unpublished ILL Search PubMed.
- J. Rodriguez-Carvajal, Physica B, 1993, 192, 55 CrossRef CAS.
- B. E. Warren, Phys. Rev., 1941, 59, 693 CrossRef CAS.
- C.-E. Chen, Y. Schlesinger and A. J. Heegar, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 25, 2472 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Full details of all the GSAS refinements performed on the powder XRD and neutron data including all refinement parameters and profiles. Additional supporting magnetic data is included. See DOI: 10.1039/c7tc05187e |
| This journal is © The Royal Society of Chemistry 2018 |