Vertically oriented TiS2−x nanobelt arrays as binder- and carbon-free intercalation electrodes for Li- and Na-based energy storage devices†
Abstract
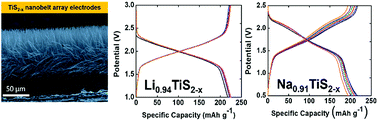
Titanium(IV) sulfide (TiS2) is a promising 2D layered material for energy storage applications. However, its electrochemical performance has been hindered by its low ion diffusion coefficient and inconsistencies in determining its electrical properties. To overcome these challenges, bulk TiS2 cathodes are normally mixed with conductive additives (typically carbon) and polymer binders (typically polyvinylidene fluoride – PVDF) to yield a paste that is subsequently cast onto a current collector. The electrochemical performance of the electrode is lowered due to the extra weight of all the inactive components (i.e., additives, polymer binder, and metal substrates) introduced during the fabrication process. An alternative to the use of pasted electrodes is the direct growth of well-defined nanostructures on a conducting substrate. In this study, we report the synthesis, characterization, and electrochemical performance of carbon- and binder-free cathodes comprising highly conducting TiS2 nanobelts. The fabricated TiS2 nanobelts are highly anisotropic and are vertically grown directly on the current collector to yield a spatially controlled array. The short ion diffusion paths, high electrical conductivity and absence of additives that hinder ion migration lead to Li- and Na-based TiS2 electrochemical devices exhibiting high specific capacity, less capacity fade, and resilience under higher cycling rates. We also present the effects of sulfur vacancies on the electrochemical performance of both vertically oriented Li- and Na-based TiS2−x nanobelt array cathode insertion hosts. It is also worth mentioning that Na-ion half-cells comprising our vertically oriented TiS2 nanobelt arrays exhibit a discharge capacity of 217 mA h g−1 (theoretical specific capacity of 239 mA h g−1). This discharge capacity equates to 0.91 Na per TiS2 unit – exceeding the maximum loading ever obtained of 0.8 Na per TiS2 under practical operation. We thus observe that scaling to finite sizes as well as fabricating highly anisotropic nanobelt arrays are found to profoundly alter both the kinetics of Li- and Na-ion insertion and the electrochemical performance of TiS2.
- This article is part of the themed collections: 2022 Journal of Materials Chemistry Lectureship runners-up: Jessica Wade and Luisa Whittaker-Brooks and Journal of Materials Chemistry A Emerging Investigators


 Please wait while we load your content...
Please wait while we load your content...