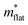Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A and B site doping of a phonon-glass perovskite oxide thermoelectric†
L. M.
Daniels
 a,
S.
Ling
a,
S.
Ling
 b,
S. N.
Savvin
a,
M. J.
Pitcher
b,
S. N.
Savvin
a,
M. J.
Pitcher
 a,
M. S.
Dyer
a,
M. S.
Dyer
 a,
J. B.
Claridge
a,
B.
Slater
a,
J. B.
Claridge
a,
B.
Slater
 b,
F.
Corà
b,
J.
Alaria
b,
F.
Corà
b,
J.
Alaria
 *c and
M. J.
Rosseinsky
*c and
M. J.
Rosseinsky
 *a
*a
aDepartment of Chemistry, University of Liverpool, Crown Street, Liverpool, L69 7ZD, UK. E-mail: m.j.rosseinsky@liverpool.ac.uk
bDepartment of Chemistry, University College London, Gower Street, London, WC1E 6BT, UK
cDepartment of Physics, University of Liverpool, Oxford Street, Liverpool, L69 7ZE, UK. E-mail: jonathan.alaria@liverpool.ac.uk
First published on 30th July 2018
Abstract
By tuning the A site cation size it is possible to control the degree of octahedral distortion and ultimately structural symmetry in the new perovskite solid solution La0.5Na0.5−xKxTiO3, affording a rhombohedral-to-cubic transition as x increases above 0.4. The La3+ and K+ cations are distributed randomly across the A site leading to significant phonon disorder in cubic La0.5K0.5TiO3 (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) which produces a phonon-glass with a thermal conductivity of 2.37(12) W m−1 K−1 at 300 K; a reduction of 75% when compared with isostructural SrTiO3. This simple cation substitution of Sr2+ for La3+ and K+ maintains the flexible structural chemistry of the perovskite structure and two mechanisms of doping for the introduction of electronic charge carriers are explored; A site doping in La1−yKyTiO3 or B site doping in La0.5K0.5Ti1−zNbzO3. The phonon-glass thermal conductivity of La0.5K0.5TiO3 is retained upon doping through both of these mechanisms highlighting how the usually strongly coupled thermal and electronic transport can be minimised by mass disorder in perovskites. Precise control over octahedral distortion in A site doped La1−yKyTiO3, which has rhombohedral (R
m) which produces a phonon-glass with a thermal conductivity of 2.37(12) W m−1 K−1 at 300 K; a reduction of 75% when compared with isostructural SrTiO3. This simple cation substitution of Sr2+ for La3+ and K+ maintains the flexible structural chemistry of the perovskite structure and two mechanisms of doping for the introduction of electronic charge carriers are explored; A site doping in La1−yKyTiO3 or B site doping in La0.5K0.5Ti1−zNbzO3. The phonon-glass thermal conductivity of La0.5K0.5TiO3 is retained upon doping through both of these mechanisms highlighting how the usually strongly coupled thermal and electronic transport can be minimised by mass disorder in perovskites. Precise control over octahedral distortion in A site doped La1−yKyTiO3, which has rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) symmetry affords lower band dispersions and increased carrier effective masses over those achieved in B site doped La0.5K0.5Ti1−zNbzO3 which maintains the cubic (Pm
c) symmetry affords lower band dispersions and increased carrier effective masses over those achieved in B site doped La0.5K0.5Ti1−zNbzO3 which maintains the cubic (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) symmetry of the undoped La0.5K0.5TiO3 parent. The higher Seebeck coefficients of A site doped La1−yKyTiO3 yield larger power factors and lead to increased thermoelectric figures of merit and improved conversion efficiencies compared with the mechanism for B site doping.
m) symmetry of the undoped La0.5K0.5TiO3 parent. The higher Seebeck coefficients of A site doped La1−yKyTiO3 yield larger power factors and lead to increased thermoelectric figures of merit and improved conversion efficiencies compared with the mechanism for B site doping.
Introduction
Thermoelectric devices convert heat energy directly into electricity or vice versa and have been utilised heavily as power sources for spacecraft and in thermoelectric heating or cooling technologies.1,2 The most important application of these devices is to the recovery of waste heat energy, particularly in the industrial, residential and automotive sectors in order to improve efficiency and sustainability.3,4 The performance of thermoelectric materials is assessed via the thermoelectric figure of merit ZT = (S2σ/κ)T comprised of the electronic conductivity (σ) and Seebeck coefficient (S), which together form the power factor (S2σ), and the thermal conductivity (κ). Optimisation of ZT is made difficult by the complex coupled relationships that exist between each of the above properties. The phonon-glass electron-crystal (PGEC) approach envisages the decoupling of σ and S, which are typically governed by the electronic Boltzmann transport equation, from κ which is governed by phonon transport within the lattice.5 “Phonon-glass” refers to the lattice contribution to the thermal conductivity (κlatt) being minimised such that heat transport in a material is hindered like in a glass, while “electron-crystal” corresponds to the retention of a high σ and S within the same material leading to charge transport like in a semiconductor. These characteristics are widely reported in intermetallic systems such as clathrates and skutterudites,6,7 which rely on the inclusion of rattler guest atoms within large structural cages to suppress κlatt while electronic transport mediated through the covalent framework remains unaffected. The PGEC concept has been recently extended to oxide thermoelectrics.8Metal oxides offer increased stability at high operating temperatures (automotive exhaust waste heat recovery typical operation temperature is 350–700 K, and industrial furnace waste heat recovery at 700–1100 K)4,9 as well as higher natural abundance and lower toxicity of the constituent elements, leading to much lower costs and smaller environmental impacts when compared with the intermetallics used currently.10,11 Titanate-based thermoelectrics, such as donor doped SrTiO3, are the current state-of-the-art n-type thermoelectric oxides with a recent report of ZT ≈ 0.6 at 1000 K which was achieved through nanoscale modulation of SrTiO3 and TiO2 inclusions in Sr0.9La0.1Ti0.9Nb0.1O3.12 The unique band structure of SrTiO3 with contributions from both heavy and light carriers at the Fermi level,13 gives rise to high power factors of 28–36 mW K−2 cm−1 at 300 K for x = 0.015–0.1 in Sr1−xLaxTiO3−δ single crystals but ZT is limited to 0.09 due to the large κ of 9–12 W m−1 K−1 in these materials.14,15 With κlatt contributing 75–100% of the total thermal conductivity, control over lattice phonon transport would allow for much higher figures of merit to be achieved in titanate perovskite thermoelectrics. SrTiO3 can be considered as a phonon crystal where heat transport is mediated by coherent and long-distance propagation of phonons through the lattice, but due to the relatively small phonon mean free path (2–3 nm) the effects of nanostructuring approaches that are widely used to reduce κ in intermetallic thermoelectrics are negated unless nanometre-sized grains are achieved.16 We highlighted previously the effectiveness of targeting a low κ that is intrinsic to the material, as opposed to originating from extrinsic microstructural effects, by exploiting the flexibility of the perovskite structure in a simple A site cation substitution that lead to a phonon-glass κ of ≈2.2 W m−1 K−1 in crystalline La0.5Na0.5TiO3.8 Through a combined experimental and computational approach, the origin of this glass-like behaviour was explained by increased phonon scattering as a result of charge and mass disorder resulting from the random distribution of La3+ and Na+. Specifically, compared against SrTiO3 the disordered cations in La0.5Na0.5TiO3 act as locally decoupled oscillators with a broad range of vibrational frequencies which ultimately lead to phonon interactions being far more localised and heat transport being much less coherent. By achieving this intrinsically low κ, it enabled the emergence of PGEC properties where thermal and electronic transport are decoupled and could be altered independently.
The unique band dispersions observed in SrTiO3 that allow for high power factors are correlated significantly with the high symmetry of the cubic structure and linearity of the Ti–O–Ti bonding.13 La0.5Na0.5TiO3 is a rhombohedrally-distorted perovskite with an ≈8° tilt of the TiO6 octahedra and non-linear Ti–O–Ti bond angles of ≈167°.8,17 This tilting decreases overlap interactions between the Ti 3d and O 2p orbitals that are responsible for the dispersion of the valence and conduction bands in SrTiO3, which decreases band dispersion thus increasing the charge carrier effective mass and in turn reducing the electronic conductivity. Symmetry considerations indicate that band dispersions are highest in the cubic perovskite phase, leading to the highest conductivity.8,13 It is a widely accepted feature of the perovskite structure that it is possible to influence the symmetry of the material by tuning the cation size, and the effect of this can be estimated through the Goldschmidt tolerance factor, t = (rA + rO)/√2(rB + rO), where the highest symmetry cubic structures have values closest to unity.18,19 By increasing the cation size on the A site of La0.5Na0.5TiO3 through substitution of Na+ for K+ (rNa+ = 1.39 Å and rK+ = 1.64 Å)20 in La0.5Na0.5−xKxTiO3, t can be increased from 0.98 closer to 1. This is a new solid solution that is not reported in the literature and very little information is available on the fully substituted end-member phase La0.5K0.5TiO3. This phase has been prepared previously through hydrothermal,21 and high-pressure synthesis,22 however detailed analysis and understanding of the structures is lacking. A cubic structure was reported by Brous et al.,23 however this was based on a non-stoichiometric composition of La0.531K0.469TiO3. We report the ceramic ambient pressure synthesis and detailed study of La0.5K0.5TiO3 and the new perovskite solid solution La0.5Na0.5−xKxTiO3. Through crystal structure engineering and tuning of A site cation size it is possible to obtain cubic symmetry leading to band dispersions optimised for maximum conductivity in the perovskite La0.5K0.5TiO3 while retaining the A site disorder that suppresses κ and leads to phonon-glass behaviour. The chemical flexibility of this material is demonstrated by donor doping on either the A or B site giving rise to electronic transport and power factors comparable to other doped titanate perovskites while the thermal conductivity remains mostly unaffected.
Experimental
Synthesis and processing of La0.5Na0.5−xKxTiO3
Pre-dried reagents of La2O3 (99.99%, Aldrich), Na2CO3 (99.997%, Alfa Aesar), K2CO3 (99.997%, Alfa Aesar) and TiO2 (99.99%, Aldrich) were weighed out on a ≈1.7 gram scale to give desired compositions. All reagents were dried overnight at 473 K before weighing, except for La2O3 which was annealed at 1223 K. The powder mixtures were ground in acetone for 10 minutes before being fired as a powder in air at 1273 K for 4 hours placed in an alumina crucible. Heating and cooling rates were 1 and 5 K min−1, respectively. The fired powders were ground for 10 minutes before being pressed uniaxially into a 13 mm pellet approximately 1 gram in mass. A portion of the powder was kept separate (≈0.7 grams) to be used as sacrificial mixture in order to minimise the loss of volatile Na2O and K2O species during sintering. The pellet was then further pressed under an isostatic pressure of 200 MPa at ambient temperature using an Autoclave Engineers Cold Isostatic Press. These cold-pressed pellets were placed in an alumina boat and buried in the sacrificial powder before being sintered for 8 hours at 1623 K in air using heating and cooling rates of 1 and 3 K min−1, respectively.Synthesis and processing of La1−yKyTiO3 and La0.5K0.5Ti1−zNbzO3
Preparation of powder mixtures for the doped materials was done using a procedure similar to that described above for La0.5Na0.5−xKxTiO3. Nb2O5 (99.9985%, Alfa Aesar) was used for the B site doped compositions. The sintering step performed at 1623 K for 8 hours, with the cold-pressed pellet buried under sacrificial powder of the same composition, was done under a 50 mL min−1 flow of H2/N2 (5/95%) instead of air in order to reduce the sample. To ensure the processing conditions were consistent for each composition, the p(O2) was monitored during each reduction step using a Cambridge Sensotec Rapidox 2100 Oxygen Analyser. The furnace was purged with flowing H2/N2 (5/95%) to achieve a p(O2) of 10−19 ppm before the pellets were sintered.Pairs of pellets for each composition were processed in the same reactions; one pellet for the measurement of thermal transport, and the other for measurement of electronic transport. Pellet densities were determined using the Archimedes method.
Characterisation
Structural analyses of the new La0.5Na0.5−xKxTiO3, La1−yKyTiO3 and La0.5K0.5Ti1−zNbzO3 materials were performed through Rietveld analysis of synchrotron X-ray powder diffraction (SXRD) data and powder neutron diffraction (PND) data. SXRD data were recorded at beamline I11 (λ = 0.82608 Å) at Diamond Light Source, U.K, with the powders contained within 0.3 mm diameter borosilicate capillaries. PND data were collected on HRPD at ISIS, the U.K. time-of-flight spallation neutron source, with the powders loaded into thin-walled cylindrical vanadium cans of 8 mm diameter. Data were measured at ambient conditions on detector banks 1 (2θ = 168°), 2 (2θ = 90°) and 3 (2θ = 30°) and were corrected for absorption effects before analysis. Rietveld refinements were carried out using Topas Academic.24 SEM images were collected using a Hitachi S-4800, cold cathode, field-emission scanning electron microscope (SEM) from pellets that were deposited on a carbon tape attached to an aluminium stub.Elemental analysis
Analysis of sample compositions was undertaken using Inductively Coupled Plasma Optical Emission Spectrometry (ICP-OES). Solutions of La1−yKyTiO3 (y = 0.5, 0.45 and 0.4) and La0.5K0.5Ti1−zNbzO3 (z = 0.05 and 0.1) were prepared through acid digestion of approximately 10 mg pieces of sintered pellet. These were dissolved in 7 mL of concentrated HCl sealed inside Teflon-lined stainless-steel Parr autoclaves which were heated to 503 K for 4 hours. These solutions were made up to 100 mL in volumetric glassware using ultra-pure water. Metal contents were corrected for interference by comparing separate and combined metal solutions of known concentrations. Data were collected on an Agilent 5110 SCDV ICP-OES instrument.Measurement of thermal conductivity
Thermal diffusivity (α) data were measured by laser flash analysis using a Netzsch LFA 457. The polished pellets (approximately 10 mm in diameter and 1.5–2 mm thick) were coated in colloidal graphitic carbon before being placed inside the sample chamber which was evacuated and purged three times before being put under a constant helium flow of 100 mL min−1. Data were collected in 50 K steps in the temperature range 298 to 943 K, with a five minute equilibration at each temperature. Three measurements were recorded at each temperature and averaged and the standard deviation of these points was typically below 0.5%. Thermal expansion profiles were measured on a Netzsch DIL 402C push-rod dilatometer under dynamic vacuum on bars approximately 4 mm in length. Continuous measurements were made from 298 to 973 K with a heating rate of 3 K min−1. Errors on dilatometry measurements are assumed to be 5% as informed by the manufacturer. Heat flux profiles were measured on small pieces of sintered pellet (≈50 mg) using a Netzsch DSC 404 F1 differential scanning calorimeter under a 50 mL min−1 flow of helium. Data were recorded from 323 to 973 K at a heating rate of 10 K min−1. Data were also measured under identical conditions from a sapphire standard (also 50 mg) which was used to determine the heat capacities (Cp) of each sample. Errors on heat capacities were assumed to be 5% as advised by the manufacturer. The thermal conductivity (κ) was calculated by combining the diffusivity, dilatometry and heat capacity data through κ(T) = α(T)Cp(T)ρ(T) where ρ is the pellet density. The total thermal conductivity (κ) is equal to the sum of the lattice (κlatt) and electronic (κelec) contributions through κ = κlatt + κelec. The electronic contribution to the thermal conductivity is estimated through the Wiedemann–Franz law which states κelec = LTσ, where L is the Sommerfield value for the Lorenz number (2.45 × 10−8 W Ω K−2), T is the temperature and σ is the electronic conductivity.25Measurement of electronic conductivity and Seebeck coefficient
Simultaneous electronic conductivity (σ) and Seebeck coefficient (S) measurements were made on an Ulvac-Riko ZEM-3 instrument from rectangular bars (dimensions of 2 × 2 × 8 mm) which were cut from sintered pellets using a low-speed diamond-blade saw. The bars were mounted in a 4-point geometry with outer current electrodes in contact with each end face and inner thermocouple and voltage probes pressed against one of the longer (8 mm) sides of the bar. The sample chamber was evacuated and purged three times with helium and then dosed with 0.01 MPa of helium before commencing measurement. Data were recorded at 50 K intervals from 323 to 973 K, applying 10, 20 and 30 K temperature gradients to the bar at each temperature step. Errors on both σ and S were assumed to be 5% on advice of the manufacturer.Phonon calculations
To achieve a better understanding of the atomistic origin of the different thermal conductivities of La0.5K0.5TO3 and SrTiO3, accurate first principles calculations were performed. All phonon calculations of La0.5K0.5TO3 (with random La/K distribution) and SrTiO3 were performed in the harmonic approximation using the code CP2K, at the density functional theory (DFT)/PBE level of theory.26,27 CP2K employs a mixed Gaussian/plane-wave basis set; in the current study, a double-ζ plus polarization quality Gaussian basis set,28 and a 400 Ry plane-wave cutoff for the auxiliary grid were employed in conjunction with Goedecker–Teter–Hutter pseudopotentials.29,30 A convergence threshold of 1.0 × 10−8 Ha was used for the self-consistent field cycle, and structural optimizations were considered to have converged when the maximum force on all atoms fell below 1.0 × 10−4 Ha per Bohr. All calculations were performed with the Γ-point approximation, using a rhombohedral supercell containing 640 atoms (lattice constants ∼ 22 Å). The second derivatives of the total energy with respect to the atomic displacements were computed numerically, from analytical first derivatives, using atomic displacements of 0.01 Bohr from the equilibrium position. Normal modes and frequencies were obtained by diagonalization of the dynamical matrix. To understand the nature of phonon modes in La0.5K0.5TiO3, the mean distance between the 10 atoms that participate to the greatest extent in a given phonon mode as defined by their displacement amplitudes were calculated, denoted as daverage, which quantifies the localisation of phonon modes and is given by: | (1) |
Electronic band structure calculations
To understand how the octahedral tilting (as present in La0.5Na0.5−xKxTiO3 for x < 0.4) modifies the band dispersions at the bottom of the conduction band, which may directly affect the thermoelectric power factor, we have performed additional DFT calculations on the electronic band structures of SrTiO3, taking it as a model system, and we consider different amounts of octahedral tilting. All electronic band structure calculations of SrTiO3 were performed using CRYSTAL14 at DFT/PBE0 level of theory.31,32 Reciprocal space sampling has been performed for all structures using a Monkhorst–Pack grid of 8 × 8 × 8 k-points. Standard all electron basis sets from the CRYSTAL online database (https//:www.crystal.unito.it) have been used for O and Ti (indicated by the following labels online: O_8−411d11G_valenzano_2006, Ti_86-411(d31)G_darco_unpub). For Sr, we have used a small-core relativistic effective core potential with a double-zeta quality valence basis set (indicated by Sr_m-S-RSC_Heyd_2005_Heyd_2005 online). The initial structure of cubic SrTiO3 in the rhombohedral cell (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) without any octahedral tilting has been fully optimised, which was then used as the starting point to generate SrTiO3 structures with octahedral tilting. The two SrTiO3 structures with different amounts of octahedral tilting were manually generated, by adjusting the oxygen fractional coordinates and lattice parameters, to ensure Ti–O bond lengths remain the same. Subsequent band structure calculations were performed for the unoptimized structures (for SrTiO3 with octahedral tilting).
c) without any octahedral tilting has been fully optimised, which was then used as the starting point to generate SrTiO3 structures with octahedral tilting. The two SrTiO3 structures with different amounts of octahedral tilting were manually generated, by adjusting the oxygen fractional coordinates and lattice parameters, to ensure Ti–O bond lengths remain the same. Subsequent band structure calculations were performed for the unoptimized structures (for SrTiO3 with octahedral tilting).
Results and discussion
Phonon-glass thermal conductivity in La0.5Na0.5−xKxTiO3
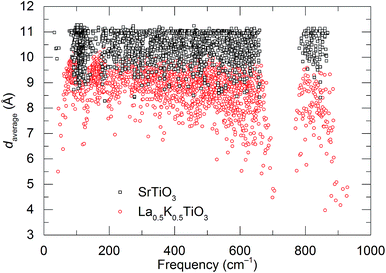
La0.5Na0.5TiO3 has a rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) perovskite structure, described by a tilting of the TiO6 octahedra about the [111] direction of the primitive cubic cell (āāā tilt system in Glazer's notation),33 and disordered A site cation distribution. Phonon calculations that previously highlighted the localisation of vibrational modes in La0.5Na0.5TiO3 were performed for La0.5K0.5TiO3. Calculation of daverage, which corresponds to the average separation between the ten atoms with largest phonon displacement amplitudes for each individual phonon mode is shown in Fig. 1 for SrTiO3 and La0.5K0.5TiO3. The results show that La0.5K0.5TiO3 has similarly promising features to those observed in La0.5Na0.5TiO3,8 indicating that the disordered distribution of La3+ and K+ leads to significant phonon localisation and should yield a phonon-glass thermal conductivity similar to La0.5Na0.5TiO3. Compared against SrTiO3 which has a daverage of ≈11 Å across the entire phonon spectrum, daverage is reduced by 15–20% in La0.5K0.5TiO3. We also showed previously how the coexisting dispersive and dispersion-less bands at the bottom of the conduction band that allow for high power factors in cubic SrTiO3 are retained in rhombohedral La0.5Na0.5TiO3. Table 1 shows relative effective masses (m*) extracted from the calculated electronic band structures of SrTiO3 at different octahedral tilt angles. The effective masses decrease with decreasing tilt angle for both bands, which shows that a cubic zero-tilt structure provides band dispersions that are optimised for highly mobile carriers towards the best possible electronic conductivity. From these computational indications, La0.5K0.5TiO3 presents a suitable low thermal conductivity target with band dispersions optimised for electronic conductivity and the structural flexibility of a perovskite to allow for carrier doping.
c) perovskite structure, described by a tilting of the TiO6 octahedra about the [111] direction of the primitive cubic cell (āāā tilt system in Glazer's notation),33 and disordered A site cation distribution. Phonon calculations that previously highlighted the localisation of vibrational modes in La0.5Na0.5TiO3 were performed for La0.5K0.5TiO3. Calculation of daverage, which corresponds to the average separation between the ten atoms with largest phonon displacement amplitudes for each individual phonon mode is shown in Fig. 1 for SrTiO3 and La0.5K0.5TiO3. The results show that La0.5K0.5TiO3 has similarly promising features to those observed in La0.5Na0.5TiO3,8 indicating that the disordered distribution of La3+ and K+ leads to significant phonon localisation and should yield a phonon-glass thermal conductivity similar to La0.5Na0.5TiO3. Compared against SrTiO3 which has a daverage of ≈11 Å across the entire phonon spectrum, daverage is reduced by 15–20% in La0.5K0.5TiO3. We also showed previously how the coexisting dispersive and dispersion-less bands at the bottom of the conduction band that allow for high power factors in cubic SrTiO3 are retained in rhombohedral La0.5Na0.5TiO3. Table 1 shows relative effective masses (m*) extracted from the calculated electronic band structures of SrTiO3 at different octahedral tilt angles. The effective masses decrease with decreasing tilt angle for both bands, which shows that a cubic zero-tilt structure provides band dispersions that are optimised for highly mobile carriers towards the best possible electronic conductivity. From these computational indications, La0.5K0.5TiO3 presents a suitable low thermal conductivity target with band dispersions optimised for electronic conductivity and the structural flexibility of a perovskite to allow for carrier doping.
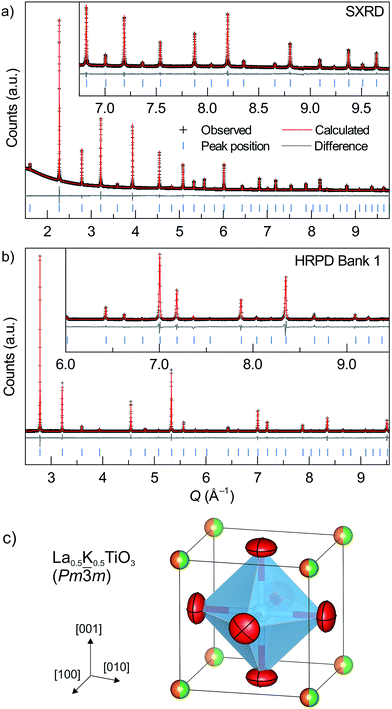
Potassium was substituted for sodium through the new solid solution La0.5Na0.5−xKxTiO3. The results of Rietveld refinement against SXRD and PND data measured on La0.5K0.5TiO3, prepared at 1300 °C through solid state synthesis, are shown in Fig. 2. The single phase powder diffraction pattern for La0.5K0.5TiO3 can be indexed to a cubic unit cell with space group symmetry Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and lattice parameter of 3.908212(5) Å. This is slightly larger than the only reported lattice parameter of 3.907 Å,23 which was based on a composition of La0.531K0.469TiO3 implying that more of the larger K+ is present in the structure reported here as evidenced by the refined occupancies (Table S1, ESI†) and presents the first structural analysis of stoichiometric La0.5K0.5TiO3. The La3+ and K+ are modelled on the 1a crystallographic position and both A and B sites are modelled using isotropic displacement parameters (Table S1, Fig. S1, ESI†). The use of anisotropic displacement parameters (ADPs) to model the 3c oxygen position yielded a small improvement to the fit, decreasing Rwp from 1.525% to 1.485%. This gave a similar equivalent Uiso (0.01446(16) Å2) to modelling the site using isotropic displacement parameters (0.01425(7) Å2) but resulted in slightly elongated ADPs displaying atomic motion perpendicular to the Ti–O–Ti direction as is expected due to thermally induced rotational motion of the BO6 octahedra.
m and lattice parameter of 3.908212(5) Å. This is slightly larger than the only reported lattice parameter of 3.907 Å,23 which was based on a composition of La0.531K0.469TiO3 implying that more of the larger K+ is present in the structure reported here as evidenced by the refined occupancies (Table S1, ESI†) and presents the first structural analysis of stoichiometric La0.5K0.5TiO3. The La3+ and K+ are modelled on the 1a crystallographic position and both A and B sites are modelled using isotropic displacement parameters (Table S1, Fig. S1, ESI†). The use of anisotropic displacement parameters (ADPs) to model the 3c oxygen position yielded a small improvement to the fit, decreasing Rwp from 1.525% to 1.485%. This gave a similar equivalent Uiso (0.01446(16) Å2) to modelling the site using isotropic displacement parameters (0.01425(7) Å2) but resulted in slightly elongated ADPs displaying atomic motion perpendicular to the Ti–O–Ti direction as is expected due to thermally induced rotational motion of the BO6 octahedra.
A rhombohedral-to-cubic transition exists within the La0.5Na0.5−xKxTiO3 series and occurs upon increasing x between 0.4 and 0.5 with La0.5K0.5TiO3 being cubic (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), and compositions of 0.1 < x < 0.4 being indexed to the same rhombohedral unit cell as La0.5Na0.5TiO3 (R
m), and compositions of 0.1 < x < 0.4 being indexed to the same rhombohedral unit cell as La0.5Na0.5TiO3 (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c). This rhombohedral-to-cubic transition that occurs between x = 0.4 and 0.5 is not immediately obvious upon examination of the c/a lattice parameter ratio shown in Fig. 3a which suggests that the unit cell becomes metrically cubic at x = 0.2 (where c/a = √6 = 2.4495), and not at x = 0.5. Only full structural analysis through Rietveld refinement can confirm that the rhombohedral structure, defined by the symmetry elements present, persists in the 0.1 < x < 0.4 compositions and that cubic symmetry is achieved only for x = 0.5. The primitive pseudocubic cell volume increases linearly towards x = 0.5 as shown in Fig. 3a. The replacement of smaller sodium with larger potassium (rNa+ = 1.39 Å and rK+ = 1.64 Å)20 increases the average cation size on the A site and causes an expansion of the unit cell. This expansion of the unit cell with increasing x results in a linear decrease in the octahedral tilt angle, ϕ, which is used to describe the rotation of the BO6 octahedra about the threefold axis of the primitive cubic cell and is determined from the convention of Megaw, ϕ = arc
c). This rhombohedral-to-cubic transition that occurs between x = 0.4 and 0.5 is not immediately obvious upon examination of the c/a lattice parameter ratio shown in Fig. 3a which suggests that the unit cell becomes metrically cubic at x = 0.2 (where c/a = √6 = 2.4495), and not at x = 0.5. Only full structural analysis through Rietveld refinement can confirm that the rhombohedral structure, defined by the symmetry elements present, persists in the 0.1 < x < 0.4 compositions and that cubic symmetry is achieved only for x = 0.5. The primitive pseudocubic cell volume increases linearly towards x = 0.5 as shown in Fig. 3a. The replacement of smaller sodium with larger potassium (rNa+ = 1.39 Å and rK+ = 1.64 Å)20 increases the average cation size on the A site and causes an expansion of the unit cell. This expansion of the unit cell with increasing x results in a linear decrease in the octahedral tilt angle, ϕ, which is used to describe the rotation of the BO6 octahedra about the threefold axis of the primitive cubic cell and is determined from the convention of Megaw, ϕ = arc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan[2√3(x − 0.5)], where x is the positional parameter of the 18e oxygen site.34Fig. 3b shows how the octahedral tilt angle decreases from 7.9142(2)° for x = 0 to 0° for x = 0.5 in La0.5Na0.5−xKxTiO3, with the rhombohedral-to-cubic transition between tilted and non-tilted structures occurring between x = 0.4 and 0.5. Alternatively, this can be viewed through the Ti–O–Ti bond angles which become more linear with x, increasing from 167.044(14)° for x = 0 to 180° in x = 0.5. While ϕ is decreasing towards 0° with increasing x, there is a simultaneous distortion of the octahedra themselves where O–Ti–O angles deviate away from the ideal 90° and can be quantified by the octahedral bond angle variance in eqn (2)35
tan[2√3(x − 0.5)], where x is the positional parameter of the 18e oxygen site.34Fig. 3b shows how the octahedral tilt angle decreases from 7.9142(2)° for x = 0 to 0° for x = 0.5 in La0.5Na0.5−xKxTiO3, with the rhombohedral-to-cubic transition between tilted and non-tilted structures occurring between x = 0.4 and 0.5. Alternatively, this can be viewed through the Ti–O–Ti bond angles which become more linear with x, increasing from 167.044(14)° for x = 0 to 180° in x = 0.5. While ϕ is decreasing towards 0° with increasing x, there is a simultaneous distortion of the octahedra themselves where O–Ti–O angles deviate away from the ideal 90° and can be quantified by the octahedral bond angle variance in eqn (2)35
 | (2) |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c allows for refinement of ADPs for the A site, which results in a slight elongation of the position along the c axis of the unit cell towards neighbouring octahedra (Fig. S1, ESI†). Despite the static disorder generated by three different cations occupying the A site, the local deviation away from the average structure is minimal with a root mean square displacement of 0.107(16) Å at 300 K. Most importantly, the structural analysis of the La0.5Na0.5−xKxTiO3 solid solution and of La0.5K0.5TiO3 in particular, shows that the La3+ and K+ are disordered across the twelve-coordinate A site. This disorder induced phonon-glass behaviour of the thermal conductivity in La0.5Na0.5TiO3,8 a property expected to be replicated in La0.5K0.5TiO3 following the observation of phonon localisation (Fig. 1).
c allows for refinement of ADPs for the A site, which results in a slight elongation of the position along the c axis of the unit cell towards neighbouring octahedra (Fig. S1, ESI†). Despite the static disorder generated by three different cations occupying the A site, the local deviation away from the average structure is minimal with a root mean square displacement of 0.107(16) Å at 300 K. Most importantly, the structural analysis of the La0.5Na0.5−xKxTiO3 solid solution and of La0.5K0.5TiO3 in particular, shows that the La3+ and K+ are disordered across the twelve-coordinate A site. This disorder induced phonon-glass behaviour of the thermal conductivity in La0.5Na0.5TiO3,8 a property expected to be replicated in La0.5K0.5TiO3 following the observation of phonon localisation (Fig. 1).
 | ||
Fig. 3 Variation in (a) c/a lattice parameter ratio (black squares) and primitive pseudocubic cell volume (red circles), (b) bond angle variance (black squares) and octahedral tilt angle (red circles), and (c) A–O distances as a function of x in the solid solution La0.5Na0.5−xKxTiO3 refined from SXRD and high resolution NPD data. Primitive cell parameters are obtained through ap = a/√2 and cp = c/2√3. Octahedral tilt angles (ϕ) are determined through ϕ = arc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan[2√3(x − 0.5)], where x is the x coordinate of the 18e oxide position in space group R tan[2√3(x − 0.5)], where x is the x coordinate of the 18e oxide position in space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c. Bond angle variance is obtained from eqn (2) in the text. c. Bond angle variance is obtained from eqn (2) in the text. | ||
La0.5K0.5TiO3 is a crystalline material that offers the high symmetry cubic structure of SrTiO3, with the unique multi-carrier band structure suited towards thermoelectricity,13 along with a disordered distribution of A site metals which have considerable mass contrast. The disorder scattering parameter is defined by Γ = ΓMF + ΓSF and contributes significantly to phonon scattering in these materials. It combines contributions from the mass contrast of defects (ΓMF) and the size strain (ΓSF) induced by ionic radius variance of defects, both of which are effective disruptors of phonon transport within a crystal lattice.37 The mass fluctuation and strain field terms are quantified through 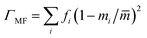 and
and 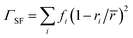 respectively, where fi is the fraction of atoms which have mass mi and radius ri occupying a crystallographic site with average mass
respectively, where fi is the fraction of atoms which have mass mi and radius ri occupying a crystallographic site with average mass ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) and average radius
and average radius ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) . Fig. 4a shows how Γ, ΓMF and ΓSF change as a function of x in La0.5Na0.5−xKxTiO3. Replacement of lighter sodium with heavier potassium results in ΓMF decreasing from 0.513 for x = 0 to 0.314 for x = 0.5, while the increased size disparity between La3+ and K+ raises ΓSF from 1.19 × 10−4 to 8.71 × 10−3 for those respective values of x. Although ΓSF is no longer negligible, with a 2.70% contribution to Γ in La0.5K0.5TiO3 compared to 0.02% in La0.5Na0.5TiO3, this increase in cation size variance is insufficient to alleviate the reduction in ΓMF that remains the dominant contribution to the total Γ, which decreases from 0.513 to 0.323 between x = 0 and 0.5, respectively. The measured thermal conductivities across the La0.5Na0.5−xKxTiO3 series are shown in Fig. 4b (Fig. S4, ESI†). One of the more striking features of the experimental data is that the thermal conductivity of the compositions in La0.5Na0.5−xKxTiO3 are not significantly different despite the reduction in Γ shown in Fig. 4a. The compositions of x = 0, 0.3 and 0.5 in La0.5Na0.5−xKxTiO3 are electronically insulating meaning that κ is equal to κlatt in these materials. The thermal conductivity of La0.5K0.5TiO3 retains the phonon-glass characteristics that were observed for La0.5Na0.5TiO3 where the temperature dependence of κlatt matches that of the heat capacity. Additionally, both the magnitude and temperature dependence of κlatt observed for La0.5K0.5TiO3 are comparable with the theoretical minimum thermal conductivity (κmin) that would be expected if SrTiO3 exhibited phonon glass properties. This quantity, compared against experimental data in Fig. 4b, is estimated through Cahill's model for disordered crystalline solids described by eqn (3)
. Fig. 4a shows how Γ, ΓMF and ΓSF change as a function of x in La0.5Na0.5−xKxTiO3. Replacement of lighter sodium with heavier potassium results in ΓMF decreasing from 0.513 for x = 0 to 0.314 for x = 0.5, while the increased size disparity between La3+ and K+ raises ΓSF from 1.19 × 10−4 to 8.71 × 10−3 for those respective values of x. Although ΓSF is no longer negligible, with a 2.70% contribution to Γ in La0.5K0.5TiO3 compared to 0.02% in La0.5Na0.5TiO3, this increase in cation size variance is insufficient to alleviate the reduction in ΓMF that remains the dominant contribution to the total Γ, which decreases from 0.513 to 0.323 between x = 0 and 0.5, respectively. The measured thermal conductivities across the La0.5Na0.5−xKxTiO3 series are shown in Fig. 4b (Fig. S4, ESI†). One of the more striking features of the experimental data is that the thermal conductivity of the compositions in La0.5Na0.5−xKxTiO3 are not significantly different despite the reduction in Γ shown in Fig. 4a. The compositions of x = 0, 0.3 and 0.5 in La0.5Na0.5−xKxTiO3 are electronically insulating meaning that κ is equal to κlatt in these materials. The thermal conductivity of La0.5K0.5TiO3 retains the phonon-glass characteristics that were observed for La0.5Na0.5TiO3 where the temperature dependence of κlatt matches that of the heat capacity. Additionally, both the magnitude and temperature dependence of κlatt observed for La0.5K0.5TiO3 are comparable with the theoretical minimum thermal conductivity (κmin) that would be expected if SrTiO3 exhibited phonon glass properties. This quantity, compared against experimental data in Fig. 4b, is estimated through Cahill's model for disordered crystalline solids described by eqn (3)
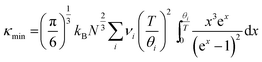 | (3) |
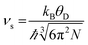 | (4) |
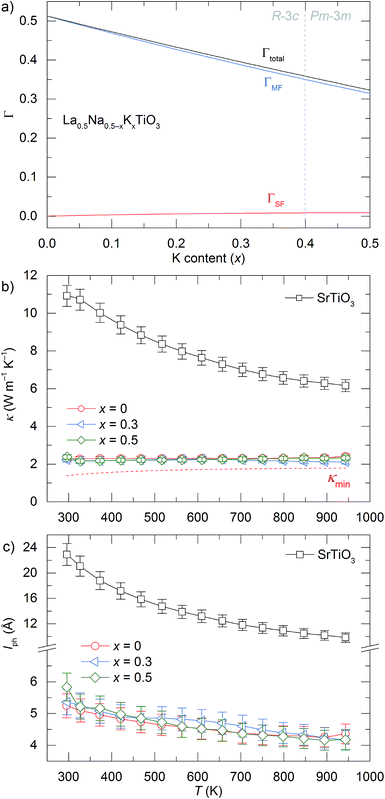 | ||
| Fig. 4 Dependence of (a) disorder scattering parameter (Γ), including mass (ΓMF) and size (ΓSF) contributions shown in blue and red respectively, (b) thermal conductivity (κ), and (c) phonon mean free path (lph) on x in the solid solution La0.5Na0.5−xKxTiO3. The theoretical minimum thermal conductivity (κmin) of SrTiO3 is shown as the dashed line in (b) and is calculated from Cahill's model for disordered crystalline solids.38 Phonon mean free paths in (c) are obtained through eqn (4) and (5). | ||
The close comparison to κmin and glass-like dependence of κlatt with temperature shows that La0.5K0.5TiO3 is a crystalline material with phonon glass thermal properties. The magnitude of κlatt at room temperature increases from 2.28 to 2.40 W m−1 K−1 from x = 0 to 0.5 respectively, which is associated with the decrease in Γ. This is only a minor change in κlatt in contrast to a considerable change to Γ, indicating that the disorder parameter has a smaller influence on the thermal conductivity in materials which display phonon-glass properties compared to those with phonon-crystal properties as was shown in Sr1−xLa0.67x□0.33xTiO3 where increasing Γ had a smaller effect as κlatt approached κmin.40 The values of κlatt observed for La0.5Na0.5−xKxTiO3 are very low when compared against both doped and undoped compositions of SrTiO3 which exhibit κlatt values in the range of 4–12 W m−1 K−1 at 300 K,41,42 and perhaps most importantly exhibit a temperature dependence that is typical of a phonon-crystal where a T−1 relationship is observed at high temperatures due to the anharmonic interaction of phonon–phonon Umklapp scattering processes. Data measured from undoped SrTiO3 is provided for comparison purposes in Fig. 4b and show that the substitution of both La3+ and K+ for Sr2+ on the A site of the perovskite structure affords a 75% reduction in thermal conductivity at 300 K (2.37(12) W m−1 K−1 for La0.5K0.5TiO3 compared against 10.91(56) W m−1 K−1 for SrTiO3). This low, glass-like thermal conductivity observed experimentally for La0.5K0.5TiO3 is consistent with the results obtained from calculations (Fig. 1) which showed that phonons are more localised in comparison with the phonon-crystal SrTiO3. The calculations, performed at DFT level, show increased contributions to the phonon density of states (PDOS) in the low frequency region in comparison with SrTiO3 (Fig. S5, ESI†). The largest contribution to the PDOS in SrTiO3 is at ≈110 cm−1, however two broader contributions are observed in this region for La0.5K0.5TiO3; a peak at ≈95 cm−1 predominantly consisting of contributions from La, and a second peak at ≈170 cm−1 arising from the contributions of K and Ti. Through this combined experimental and computational understanding of phonon behaviour in La0.5K0.5TiO3, it is clear the vibrational disorder introduced by having two high-mass contrast cations present on a single crystallographic position is highly effective at scattering phonons and reducing heat transport within the lattice, leading to the observed glass-like thermal conductivity in crystalline La0.5K0.5TiO3. This increased localisation of phonons is similar to that observed in La0.5Na0.5TiO3,8 and shows that the disordered La3+ and K+ cations in La0.5K0.5TiO3 are responsible for the phonon-glass behaviour by acting as decoupled local oscillators with incoherent phases which dramatically reduce time and distance between phonon scattering events. Experimentally, this is evident from the phonon mean free paths that are shown in Fig. 4c and are calculated from eqn (4) and (5) using θD of 630 K.43
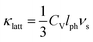 | (5) |
Introduction of electronic charge carriers into La0.5K0.5TiO3
One of the more useful features resulting from the complete replacement of Sr2+ for a charge balanced mixture of La3+ and K+ in La0.5K0.5TiO3 is that the chemical and structural flexibility of the perovskite structure is maintained. Electron doping in SrTiO3 involves the incorporation of an aliovalent cation with higher charge, such as Ln3+ on the A site or Nb5+ on the B site,42,45,46 which through charge compensation mechanisms reduces a sufficient amount of Ti4+ to Ti3+ giving rise to electronic transport. Even though the A site in La0.5K0.5TiO3 has a disordered cation arrangement, the flexible structural chemistry enables the introduction of electronic carriers through doping of either the A or B site. Incorporation of Nb5+ onto the B site through La0.5K0.5Ti1−zNbzO3 allows for the mechanisms that govern the thermal and electronic properties to be confined to the separate A and B sites of the perovskite structure, respectively, as was reported for PGEC La0.5Na0.5Ti1−xNbxO3.8 Doping of the A site can be achieved by targeting non-stoichiometric compositions through La1−yKyTiO3 (with y < 0.5). This maintains the mass contrast that affords the phonon-glass thermal conductivity, and usefully allows for the same nominal charge carrier concentrations as La0.5K0.5Ti1−zNbzO3 to be accessed by using smaller dopant amounts due to the nature of the dopant mechanisms which are described by Kröger–Vink notation in reaction eqn (6) and (7), where A and B refer to the site occupied.For La1−yKyTiO3:
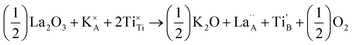 | (6) |
For La0.5K0.5Ti1−zNbzO3:
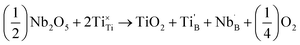 | (7) |
Through solid state reaction performed at 1300 °C under a H2/N2 (5%) atmosphere, it is possible to produce phase pure samples of La1−yKyTiO3 with 0.4 ≤ y ≤ 0.5 and La0.5K0.5Ti1−zNbzO3 up to z = 0.1. These values define the limits of doping for each material under these particular synthetic conditions; decreasing y below 0.4 in La1−yKyTiO3 results in the formation of La2Ti2O7 impurities, while increasing z further than 0.1 yields LaNbO4 as an impurity phase in La0.5K0.5Ti1−zNbzO3. The effects of A and B site doping upon the unit cell parameters of La1−yKyTiO3 and La0.5K0.5Ti1−zNbzO3 are shown in Fig. 5a and b, respectively. A linear decrease in unit cell volume is observed as a function of La3+ content in La1−yKyTiO3 associated with the larger K+ cation being replaced with La3+ (rK+ = 1.64 Å and rLa3+ = 1.36 Å).20 Both La1−yKyTiO3 compositions are indexed to rhombohedral R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c symmetry with separation of primitive cell parameters ap and cp, shown in Fig. 5a (Tables S6–S8, Fig. S7 and S8, ESI†). This distortion away from the cubic symmetry of the La0.5K0.5TiO3 parent results from the decreasing average cation size on the A site, as well as an increasing cation size on the B site from the reduction of Ti4+ to Ti3+ (rTi4+ = 0.605 Å and rTi3+ = 0.67 Å); the tolerance factor can be reduced by decreasing rA or increasing rB. Contrary to this, the cubic symmetry of the La0.5K0.5TiO3 parent is maintained in the B site doped La0.5K0.5Ti1−zNbzO3 materials up to z = 0.1 with a linear increase in the unit cell parameter and volume shown in Fig. 5b (Tables S9–S11, Fig. S9 and S10, ESI†), consistent with the substitution of Ti4+ with larger Nb5+ (rTi4+ = 0.605 Å and rNb5+ = 0.64 Å). There remains no evidence for ordering of the A site cations even in non-stoichiometric La1−yKyTiO3, indicating that the disordered distributions of La3+ and K+, which we have shown to be essential for the phonon glass κ in these materials, are preserved in all materials reported in this study. The refined oxygen occupancies for the A and B doped materials studied through both SXRD and NPD did not provide any evidence for oxide deficiencies (Tables S7 and S10, ESI†). When refined, values within error of a fully occupied oxygen position were obtained much like the oxygen occupancies in the undoped materials La0.5K0.5TiO3 and La0.5Na0.2K0.3TiO3 (Tables S1 and S2, ESI†).
c symmetry with separation of primitive cell parameters ap and cp, shown in Fig. 5a (Tables S6–S8, Fig. S7 and S8, ESI†). This distortion away from the cubic symmetry of the La0.5K0.5TiO3 parent results from the decreasing average cation size on the A site, as well as an increasing cation size on the B site from the reduction of Ti4+ to Ti3+ (rTi4+ = 0.605 Å and rTi3+ = 0.67 Å); the tolerance factor can be reduced by decreasing rA or increasing rB. Contrary to this, the cubic symmetry of the La0.5K0.5TiO3 parent is maintained in the B site doped La0.5K0.5Ti1−zNbzO3 materials up to z = 0.1 with a linear increase in the unit cell parameter and volume shown in Fig. 5b (Tables S9–S11, Fig. S9 and S10, ESI†), consistent with the substitution of Ti4+ with larger Nb5+ (rTi4+ = 0.605 Å and rNb5+ = 0.64 Å). There remains no evidence for ordering of the A site cations even in non-stoichiometric La1−yKyTiO3, indicating that the disordered distributions of La3+ and K+, which we have shown to be essential for the phonon glass κ in these materials, are preserved in all materials reported in this study. The refined oxygen occupancies for the A and B doped materials studied through both SXRD and NPD did not provide any evidence for oxide deficiencies (Tables S7 and S10, ESI†). When refined, values within error of a fully occupied oxygen position were obtained much like the oxygen occupancies in the undoped materials La0.5K0.5TiO3 and La0.5Na0.2K0.3TiO3 (Tables S1 and S2, ESI†).
The metal contents for each of the doped materials were determined using ICP-OES and are listed in Table 2. Both the La/K and Ti/Nb ratios agree very well with those from the nominal compositions, and compare closely to the refined occupancies obtained from Rietveld analysis of SXRD and PND data (Tables S1 and S6–S10, ESI†). The analysis shows near-stoichiometric ratios for La and K in the undoped La0.5K0.5TiO3 parent, in contrast to the single previous report of cubic La0.531K0.469TiO3, in which not all of the alkali metal was incorporated into the structure.23
| Nominal composition | La | K | Ti | Nb |
|---|---|---|---|---|
| La0.5K0.5TiO3 | 0.518(3) | 0.507(5) | 1.000(5) | — |
| La0.55K0.45TiO3 | 0.556(3) | 0.445(2) | 1.000(5) | — |
| La0.6K0.4TiO3 | 0.608(3) | 0.413(2) | 1.000(7) | — |
| La0.5K0.5Ti0.95Nb0.05O3 | 0.505(2) | 0.493(4) | 0.950(3) | 0.0487(1) |
| La0.5K0.5Ti0.9Nb0.1O3 | 0.507(7) | 0.469(2) | 0.900(6) | 0.0981(1) |
The sintering of cold-pressed pellets of La1−yKyTiO3 and La0.5K0.5Ti1−zNbzO3 compositions at 1350 °C under a H2/N2 (5%) atmosphere yielded ceramics with measured densities higher than 90% of the values expected from structural analysis (Table S12, ESI†), and SEM imaging showed the pellets to have minimal porosity (Fig. S6, ESI†).
The temperature dependences of the thermal conductivity for doped La1−yKyTiO3 and La0.5K0.5Ti1−zNbzO3 compositions are shown in Fig. 6a. These materials exhibit low phonon-glass thermal conductivities comparable to that of undoped La0.5K0.5TiO3 despite possessing electron carrier concentrations, determined from nominal compositions, which lie within the range expected for heavily doped semiconductors (1019 to 1021 cm−3). The thermal conductivities have magnitudes of 2.45(12)–2.65(13) W m−1 K−1 at room temperature and 2.45(12)–2.80(15) W m−1 K−1 at 850 K and have a temperature dependence like κmin determined from eqn (3). In contrast to the thermal conductivities of La1−yKyTiO3 and La0.5K0.5Ti1−zNbzO3 which show no correlation with doping, the electronic conductivities and Seebeck coefficients display a strong doping dependence shown in Fig. 6b and c. In La0.5K0.5Ti1−zNbzO3, peak conductivities increase from 180(9) to 212(10) S cm−1 at 600 K for z = 0.05 and 0.1 respectively, whereas the peak values of σ in La1−yKyTiO3 increase from 230(11) S cm−1 for y = 0.45 to 315(16) S cm−1 for y = 0.4 at 500 K, associated with increasing carrier concentration. The observed temperature dependencies of both σ and S for all compositions are similar to many doped titanate thermoelectrics reported in the literature.40,42,46,47 Maxima in σ are observed between 500–600 K and are associated with increased resistance from acceptor-based phases which are localised to the grain boundaries.48 The negative values of S indicate electron doping of predominantly n-type carriers within all compositions, and both A and B site doped materials exhibit decreasing |S| with increasing carrier concentration which is expected for metals or parabolic band semiconductors through eqn (8)
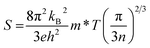 | (8) |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) structure (Table S11, ESI†). This maximises band dispersion and therefore σ, but leads to a lower m* which supports the decreased |S| observed experimentally for La0.5K0.5Ti1−zNbzO3. In contrast, the change of symmetry to R
m) structure (Table S11, ESI†). This maximises band dispersion and therefore σ, but leads to a lower m* which supports the decreased |S| observed experimentally for La0.5K0.5Ti1−zNbzO3. In contrast, the change of symmetry to R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c in La1−yKyTiO3 reduces the orbital overlap through octahedral tilting which reduces band dispersion yielding a larger m* and is the reason that higher |S| values are observed for La1−yKyTiO3 compared to La0.5K0.5Ti1−zNbzO3. The decrease in σ that a larger m* is expected to bring about is offset by the increased overlap between neighbouring Ti 3d-t2g orbitals in the smaller, more distorted cell of La1−yKyTiO3 which accounts for the closely matched conductivities observed for La0.55K0.45TiO3 and La0.5K0.5Ti0.9Nb0.1O3.42,50 Using the additional data available from the previous report of La0.5Na0.5Ti1−xNbxO3,8 it is possible to observe the relationship between |S| and octahedral tilt angle, which is plotted in Fig. 6d for compositions with the same nominal carrier concentration and further highlights the effects of tilting on band dispersions discussed above. La0.5K0.5Ti0.9Nb0.1O3 is cubic (Pm
c in La1−yKyTiO3 reduces the orbital overlap through octahedral tilting which reduces band dispersion yielding a larger m* and is the reason that higher |S| values are observed for La1−yKyTiO3 compared to La0.5K0.5Ti1−zNbzO3. The decrease in σ that a larger m* is expected to bring about is offset by the increased overlap between neighbouring Ti 3d-t2g orbitals in the smaller, more distorted cell of La1−yKyTiO3 which accounts for the closely matched conductivities observed for La0.55K0.45TiO3 and La0.5K0.5Ti0.9Nb0.1O3.42,50 Using the additional data available from the previous report of La0.5Na0.5Ti1−xNbxO3,8 it is possible to observe the relationship between |S| and octahedral tilt angle, which is plotted in Fig. 6d for compositions with the same nominal carrier concentration and further highlights the effects of tilting on band dispersions discussed above. La0.5K0.5Ti0.9Nb0.1O3 is cubic (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) with zero tilt, while both La0.55K0.45TiO3 and La0.5Na0.5Ti0.9Nb0.1O3 are rhombohedral (R
m) with zero tilt, while both La0.55K0.45TiO3 and La0.5Na0.5Ti0.9Nb0.1O3 are rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) with tilt angles of 2.18(1)° and 7.45(3)° respectively. The magnitude of |S| increases with increasing tilt angle at all temperatures with a ≈60 μV K−1 difference between La0.5K0.5Ti0.9Nb0.1O3 and La0.5Na0.5Ti0.9Nb0.1O3 due to increased m* as a result of reduced orbital overlap brought about by octahedral tilting. In contrast to the clear relationship between |S| and the tilt angle, similar magnitudes of σ are observed for these materials with the same nominal carrier concentration. From this it is clear that despite targeting high carrier mobility by tuning the symmetry of the unit cell to maximise band dispersions in the zero-tilt structure of La0.5K0.5TiO3, the optimisation of σ is far more complex and depends significantly on the processing conditions of the measured ceramics with extrinsic factors such as grain boundary resistance ultimately dominating σ.42,48 The Seebeck coefficient, measured at zero current transport, should be insensitive to grain boundary effects and exhibits a clear correlation to the octahedral tilt angle.
c) with tilt angles of 2.18(1)° and 7.45(3)° respectively. The magnitude of |S| increases with increasing tilt angle at all temperatures with a ≈60 μV K−1 difference between La0.5K0.5Ti0.9Nb0.1O3 and La0.5Na0.5Ti0.9Nb0.1O3 due to increased m* as a result of reduced orbital overlap brought about by octahedral tilting. In contrast to the clear relationship between |S| and the tilt angle, similar magnitudes of σ are observed for these materials with the same nominal carrier concentration. From this it is clear that despite targeting high carrier mobility by tuning the symmetry of the unit cell to maximise band dispersions in the zero-tilt structure of La0.5K0.5TiO3, the optimisation of σ is far more complex and depends significantly on the processing conditions of the measured ceramics with extrinsic factors such as grain boundary resistance ultimately dominating σ.42,48 The Seebeck coefficient, measured at zero current transport, should be insensitive to grain boundary effects and exhibits a clear correlation to the octahedral tilt angle.
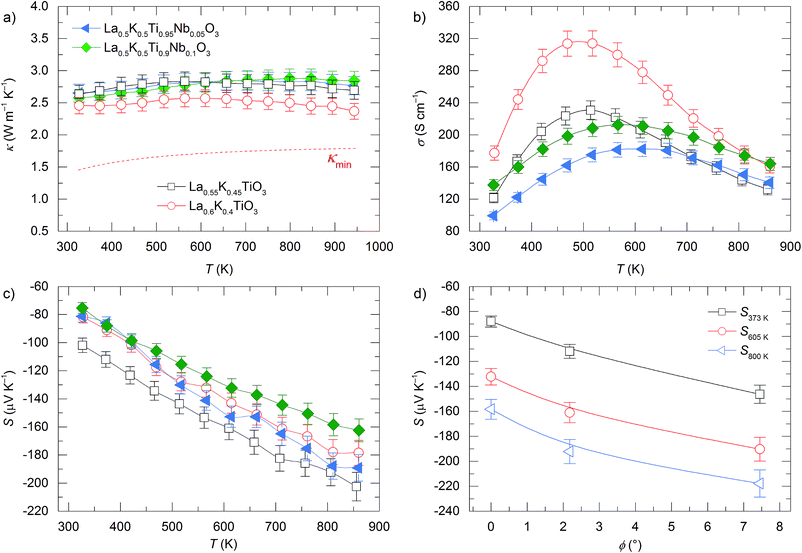 | ||
Fig. 6 Temperature dependence of (a) thermal conductivity (κ), (b) electronic conductivity (σ), and (c) Seebeck coefficient (S) for A site (La1−yKyTiO3, y = 0.45 and 0.4) and B site (La0.5K0.5Ti1−zNbzO3, z = 0.05 and 0.1) doped compositions of La0.5K0.5TiO3. Dependence of S as a function of tilt angle (ϕ) at different temperatures is shown in (d) using three materials that have the same nominal carrier concentration: La0.5K0.5Ti0.9Nb0.1O3 (ϕ = 0°) and La0.55K0.45TiO3 (ϕ = 2.18(1)°) from this study, and La0.5Na0.5Ti0.9Nb0.1O3 (ϕ = 7.45(3)°) which was taken from a recent study of PGEC La0.5Na0.5Ti1−xNbxO3 materials with R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c symmetry.8 c symmetry.8 | ||
As a result of the improved |S| values observed for La1−yKyTiO3 significant differences are observed between the power factors of the A and B site doped materials as shown in Fig. 7a. Enhancements in σ, particularly at low temperatures, alongside the increased m* and |S| in La1−yKyTiO3 result in a power factors of 0.58(5) mW m−1 K−2 at 600 K compared to 0.39(3) mW m−1 K−2 in La0.5K0.5Ti1−zNbzO3. The observation of improved power factors in titanate perovskite thermoelectrics with smaller, more-distorted unit cells is commonplace; S2σ was enhanced with increasing values of x in the solid solution Ba0.9−xSrxLa0.1TiO3,51 and the largest S2σ values were achieved for the smallest lanthanides studied in Sr0.9R0.1TiO3−δ.42 In this study, when considering both σ and S, the electronic transport is improved in La1−yKyTiO3 compositions (y = 0.45 and 0.4) across the entire measured temperature range compared to B site doped La0.5K0.5Ti1−zNbzO3 as shown in Fig. 7a and is ascribed to the improved Seebeck coefficients which result from lower band dispersions and higher m* in the more distorted structures of La1−yKyTiO3. The power factors of the La1−yKyTiO3 series are comparable to those of La0.5Na0.5Ti1−xNbxO3 reported previously.8
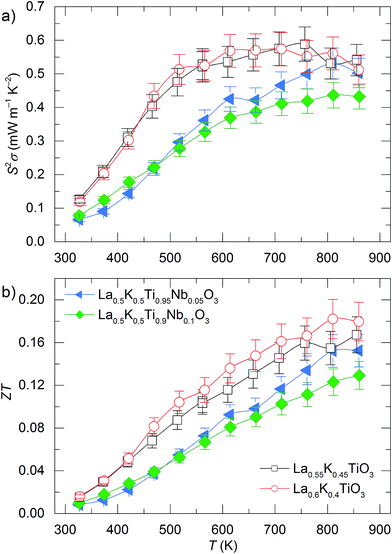 | ||
| Fig. 7 Temperature dependence of (a) thermoelectric power factors (S2σ) and (b) thermoelectric figures of merit (ZT) for La1−yKyTiO3 and La0.5K0.5Ti1−zNbzO3 compositions. | ||
Even though higher power factors are achieved for La1−yKyTiO3 compared against La0.5K0.5Ti1−zNbzO3, both series retain the same glass-like thermal conductivity of the undoped La0.5K0.5TiO3 parent and the electronic contribution to the thermal conductivity (κelec) is no larger than 12% for all samples (Fig. S11, ESI†). This highlights the weak correlation between electronic and thermal transport within these materials, properties that are usually very strongly coupled in titanate thermoelectrics with κelec contributing ≈25% of the total thermal conductivity in similarly doped Sr1−xLaxTiO3−δ,15 and again demonstrates the advantage of utilising cation mass disorder to control κlatt which remains the dominant contributor to κ in these materials.
Peak ZT values of ≈0.18 are observed at 800 K in La1−yKyTiO3 compositions and the figures of merit increase with temperature for all materials, as shown in Fig. 7b. These are slightly lower than the highest values obtained previously from La0.5Na0.5Ti1−xNbxO3 and result from the combination of comparable power factors and slightly higher thermal conductivities in La1−yKyTiO3 and La0.5K0.5Ti1−zNbzO3. The improved performance of A site doped La1−yKyTiO3 over B site doped La0.5K0.5Ti1−zNbzO3 is clear, not only in peak ZT but also for the entire measurement range. This increased figure of merit is attributed to the enhanced power factors (Fig. 7a) which originate from decreased band dispersions in more distorted La1−yKyTiO3 materials. At all temperatures, the ZT values of La1−yKyTiO3 are typically 20–50% higher than those of La0.5K0.5Ti1−zNbzO3 with the largest differences in the intermediate temperature range (350–700 K). As a result of this, the average energy conversion efficiencies (εave) of La1−yKyTiO3 are a respectable 1.39–1.59%, for y = 0.45 and 0.4 respectively, compared against 0.093–0.097% for in La0.5K0.5Ti1−zNbzO3 respectively, when evaluated through eqn (9) over the temperature ranges applicable to the recovery of waste heat from automotive exhausts.4
 | (9) |
The large difference in efficiencies between La1−yKyTiO3 and La0.5K0.5Ti1−zNbzO3 is due to the increased figures of merit across the temperature range 350–700 K, and not due to the highest peak value. The importance of ZTaverage, particularly for application temperature ranges, is frequently overlooked when searching for new peak ZT materials.
Conclusions
This work presents the study of a new solid solution between phonon-glass La0.5Na0.5TiO3 (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) and La0.5K0.5TiO3 (Pm
c) and La0.5K0.5TiO3 (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). It is possible to tune the cation size on the A site in order to target the cubic structure with linear Ti–O–Ti bonding that is associated with the high electronic conductivity of SrTiO3 based thermoelectrics. La0.5K0.5TiO3 is the first reported cubic phonon-glass titanate thermoelectric. The phonon-glass thermal conductivity results from localised phonon interactions caused by the disordered distribution of high mass contrast La3+ and K+. Electronic carriers can be introduced through either A or B site doping in La1−yKyTiO3 and La0.5K0.5Ti1−zNbzO3, respectively. The A site doping through La1−yKyTiO3 leads to larger power factors and a higher overall ZT performance compared to B site doped La0.5K0.5Ti1−zNbzO3. We find that the electronic conductivity is dominated by extrinsic effects such as grain boundary resistance despite band dispersions being optimised through the cubic symmetry of La0.5K0.5TiO3. The Seebeck coefficient is unaffected by the extrinsic factors and this performance gain is associated with the more distorted and lower symmetry structures of La1−yKyTiO3 (R
m). It is possible to tune the cation size on the A site in order to target the cubic structure with linear Ti–O–Ti bonding that is associated with the high electronic conductivity of SrTiO3 based thermoelectrics. La0.5K0.5TiO3 is the first reported cubic phonon-glass titanate thermoelectric. The phonon-glass thermal conductivity results from localised phonon interactions caused by the disordered distribution of high mass contrast La3+ and K+. Electronic carriers can be introduced through either A or B site doping in La1−yKyTiO3 and La0.5K0.5Ti1−zNbzO3, respectively. The A site doping through La1−yKyTiO3 leads to larger power factors and a higher overall ZT performance compared to B site doped La0.5K0.5Ti1−zNbzO3. We find that the electronic conductivity is dominated by extrinsic effects such as grain boundary resistance despite band dispersions being optimised through the cubic symmetry of La0.5K0.5TiO3. The Seebeck coefficient is unaffected by the extrinsic factors and this performance gain is associated with the more distorted and lower symmetry structures of La1−yKyTiO3 (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) compositions which decrease band dispersion and lead to higher effective masses and Seebeck coefficients compared with La0.5K0.5Ti1−zNbzO3 (Pm
c) compositions which decrease band dispersion and lead to higher effective masses and Seebeck coefficients compared with La0.5K0.5Ti1−zNbzO3 (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). Phonon-glass thermal conductivities are retained for both A and B site doped materials providing a further example of how intrinsic cation mass disorder can minimise the correlation between the usually strongly coupled thermal and electronic transport in perovskites and yield PGEC behaviour in a cubic titanate thermoelectric. The control of power factors through the distortion of the unit cell could provide guidance in the choice of future target materials, such as combining high mass contrast compositions with smaller cations to target improved electronic transport (e.g. Ln0.5A0.5TiO3 where A = Na+/K+, and Ln = Dy3+/Ho3+).
m). Phonon-glass thermal conductivities are retained for both A and B site doped materials providing a further example of how intrinsic cation mass disorder can minimise the correlation between the usually strongly coupled thermal and electronic transport in perovskites and yield PGEC behaviour in a cubic titanate thermoelectric. The control of power factors through the distortion of the unit cell could provide guidance in the choice of future target materials, such as combining high mass contrast compositions with smaller cations to target improved electronic transport (e.g. Ln0.5A0.5TiO3 where A = Na+/K+, and Ln = Dy3+/Ho3+).
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank EPSRC for funding under EP/N004884. We thank the Materials Chemistry Consortium (EPSRC: EP/L000202) for provision of computer time on ARCHER UK National Supercomputing Service. We thank Diamond Light Source and ISIS for provision of beamtime, and Claire Murray, Sarah Day and Paul Henry for assistance on the I11 and HRPD instruments. Marco Zanella is thanked for measurement of SEM images.Notes and references
- S. Hebert, D. Berthebaud, R. Daou, Y. Breard, D. Pelloquin, E. Guilmeau, F. Gascoin, O. Lebedev and A. Maignan, J. Phys.: Condens. Matter, 2016, 28, 013001 CrossRef PubMed.
- T. M. Tritt and M. A. Subramanian, MRS Bull., 2011, 31, 188–198 CrossRef.
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114 CrossRef PubMed.
- J. Yang and T. Caillat, MRS Bull., 2011, 31, 224–229 CrossRef.
- G. A. Slack, CRC Handbook of Thermoelectrics, CRC, Boca Raton, 1995 Search PubMed.
- M. Christensen, A. B. Abrahamsen, N. B. Christensen, F. Juranyi, N. H. Andersen, K. Lefmann, J. Andreasson, C. R. Bahl and B. B. Iversen, Nat. Mater., 2008, 7, 811–815 CrossRef PubMed.
- M. M. Koza, M. R. Johnson, R. Viennois, H. Mutka, L. Girard and D. Ravot, Nat. Mater., 2008, 7, 805–810 CrossRef PubMed.
- L. M. Daniels, S. N. Savvin, M. J. Pitcher, M. S. Dyer, J. B. Claridge, S. Ling, B. Slater, F. Cora, J. Alaria and M. J. Rosseinsky, Energy Environ. Sci., 2017, 10, 1917–1922 RSC.
- S. LeBlanc, S. K. Yee, M. L. Scullin, C. Dames and K. E. Goodson, Renewable Sustainable Energy Rev., 2014, 32, 313–327 CrossRef.
- R. Boston, W. L. Schmidt, G. D. Lewin, A. C. Iyasara, Z. Lu, H. Zhang, D. C. Sinclair and I. M. Reaney, Chem. Mater., 2016, 29, 265–280 CrossRef.
- J. W. Fergus, J. Eur. Ceram. Soc., 2012, 32, 525–540 CrossRef.
- J. Wang, B.-Y. Zhang, H.-J. Kang, Y. Li, X. Yaer, J.-F. Li, Q. Tan, S. Zhang, G.-H. Fan, C.-Y. Liu, L. Miao, D. Nan, T.-M. Wang and L.-D. Zhao, Nano Energy, 2017, 35, 387–395 CrossRef.
- K. Shirai and K. Yamanaka, J. Appl. Phys., 2013, 113, 053705 CrossRef.
- S. Ohta, T. Nomura, H. Ohta, M. Hirano, H. Hosono and K. Koumoto, Appl. Phys. Lett., 2005, 87, 092108 CrossRef.
- T. Okuda, K. Nakanishi, S. Miyasaka and Y. Tokura, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 113104 CrossRef.
- Y. Wang, K. Fujinami, R. Zhang, C. Wan, N. Wang, Y. Ba and K. Koumoto, Appl. Phys. Express, 2010, 3, 031101 CrossRef.
- R. Garg, A. Senyshyn, H. Boysen and R. Ranjan, J. Phys.: Condens. Matter, 2008, 20, 505215 CrossRef.
- V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485 CrossRef.
- R. H. Mitchell, Perovskites: Modern and Ancient, Almaz Press Inc., Thunder Bay, ON, Canada, 2002 Search PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- W. Zhao, G. Zhu, W. Zhao, T. Lin, F. Xu and F. Huang, Dalton Trans., 2015, 44, 18665–18670 RSC.
- J.-P. Miao, Z. Lü, L.-P. Li, F.-L. Ning, Z.-G. Liu, X.-Q. Huang, Y. Sui, Z.-N. Qian and W.-H. Su, J. Alloys Compd., 2005, 387, 287–291 CrossRef.
- J. Brous, I. Fankuchen and E. Banks, Acta Crystallogr., 1953, 6, 67–70 CrossRef.
- A. A. Coelho, J. Appl. Crystallogr., 2000, 33, 899–908 CrossRef.
- G. V. Chester and A. Thellung, Proc. Phys. Soc., London, 1961, 77, 1005–1013 CrossRef.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef PubMed.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef.
- S. Godecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703 CrossRef.
- M. Krack, Theor. Chem. Acc., 2005, 114, 145–152 Search PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef.
- R. Dovesi, R. Orlando, A. Erba, C. M. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. De La Pierre, P. D'Arco, Y. Noël, M. Causà, M. Rérat and B. Kirtman, Int. J. Quantum Chem., 2014, 114, 1287–1317 CrossRef.
- A. M. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392 CrossRef.
- H. D. Megaw and C. N. W. Darlington, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1975, 31, 161–173 CrossRef.
- K. Robinson, G. V. Gibbs and P. H. Ribbe, Science, 1971, 172, 567–570 CrossRef PubMed.
- Y. A. Abramov, V. G. Tsirelson, V. E. Zavodnik, S. A. Ivanoc and I. D. Brown, Acta Crystallogr., Sect. B: Struct. Sci., 1995, 51, 942–951 CrossRef.
- E. S. Toberer, A. Zevalkink and G. J. Snyder, J. Mater. Chem., 2011, 21, 15843–15852 RSC.
- D. G. Cahill, S. K. Watson and R. O. Pohl, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6131–6140 CrossRef.
- W. Kaiser and R. Zurek, Phys. Lett., 1966, 23, 668 CrossRef.
- S. R. Popuri, A. J. M. Scott, R. A. Downie, M. A. Hall, E. Suard, R. Decourt, M. Pollet and J. W. G. Bos, RSC Adv., 2014, 4, 33720–33723 RSC.
- S. Bhattacharya, A. Mehdizadeh Dehkordi, S. Tennakoon, R. Adebisi, J. R. Gladden, T. Darroudi, H. N. Alshareef and T. M. Tritt, J. Appl. Phys., 2014, 115, 223712 CrossRef.
- A. V. Kovalevsky, A. A. Yaremchenko, S. Populoh, P. Thiel, D. P. Fagg, A. Weidenkaff and J. R. Frade, Phys. Chem. Chem. Phys., 2014, 16, 26946–26954 RSC.
- L. Feng, T. Shiga and J. Shiomi, Appl. Phys. Express, 2015, 8, 071501 CrossRef.
- T. M. Tritt, Thermal Conductivity: Theory, Properties and Applications, Kluwer Academic, New York, USA, 2004 Search PubMed.
- A. A. Yaremchenko, S. Populoh, S. G. Patrício, J. Macías, P. Thiel, D. P. Fagg, A. Weidenkaff, J. R. Frade and A. V. Kovalevsky, Chem. Mater., 2015, 27, 4995–5006 CrossRef.
- B. Zhang, J. Wang, T. Zou, S. Zhang, X. Yaer, N. Ding, C. Liu, L. Miao, Y. Li and Y. Wu, J. Mater. Chem. C, 2015, 3, 11406–11411 RSC.
- T. Q. Thong, L. T. T. Huong and N. T. Tinh, Mater. Trans., 2015, 56, 1365–1369 CrossRef.
- R. Moos and K. H. Härdtl, J. Appl. Phys., 1996, 80, 393–400 CrossRef.
- A. Cammarata and J. M. Rondinelli, J. Chem. Phys., 2014, 141, 114704 CrossRef PubMed.
- J. B. Goodenough, J. Appl. Phys., 1966, 37, 1415–1422 CrossRef.
- H. Muta, K. Kurosaki and S. Yamanaka, J. Alloys Compd., 2004, 368, 22–24 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ta03739f |
| This journal is © The Royal Society of Chemistry 2018 |