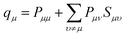A systematic evaluation of the role of lanthanide elements in functional complex oxides; implications for energy conversion devices

Abstract

Lanthanide containing complex oxides, especially the ABO₃ perovskite and A_(n+1)B_nO_(3n+1) Ruddlesden–Popper series, attract much interest as promising catalytic materials in many renewable energy applications such as electro-chemical energy conversion and hydrogen production. Recent experimental and theoretical studies on some members of these materials, e.g. La₂NiO₄, revealed that the La–O terminated surfaces are catalytically active under operational conditions. These findings suggested that the conventional understanding of such oxides being fully ionized, and composed of catalytically inert La³⁺ ions needs to be revised. In this study, generalized gradient approximation and hybrid density functional theory methods were used to study and compare the electronic structures of La and Sr in related oxides. Density functional theory approaches based on both Gaussian and plane wave basis sets were employed to ensure robustness of this study. Consistent results were obtained across different ab initio methods and approaches used. Density of states plots and charge analysis results showed that La exhibits a partially occupied d-orbital and an atomic charge of +2 instead of its nominal valence number (+3) in the oxides, while Sr does not show similar characteristics. Electron density maps obtained from synchrotron X-ray diffraction experiments confirmed the simulation findings as well. The presence of the available d-orbital electron on La and associated partial covalency were postulated as being responsible for the catalytic behaviour observed in experiments. In addition, Pr and Ba electronic structures in related oxides were also calculated. A similar trend to the La and Sr charges was observed. Based on these findings, the traditional concept of atomic “ionicity” was briefly reviewed and adapted as a catalysis descriptor for possible performance evaluation.

---

Introduction

Perovskite and Ruddlesden–Popper (RP) oxides are families of complex oxides that have a variety of attractive electrical and chemical properties such as highly tunable electrical resistance,¹ colossal magnetoresistance,² superconductivity,^3,4 catalytical properties⁵ and oxygen ionic conductivity.^6–9 These properties are of interest in many clean energy applications. Perovskite oxides have the general chemical formula ABO₃, where A is usually a large cation from group 1, 2 or 3 of the periodic table and B is a smaller metal cation. The structure of an ideal perovskite oxide consists of a BO₆ octahedron unit contained in a simple cubic cell, where the A cations occupy the cell corners. Ruddlesden–Popper oxides are extended perovskite oxides with the general formula A_(n+1)B_nO_(3n+1) or (ABO₃)_nAO. These oxides are comprised of alternating layers of ABO₃ perovskites and an AO rocksalt structure along the <001> crystallographic direction. Between a pair of AO layers, RP oxides can contain n layers of ABO₃ structure where n can be 1, 2, 3 or more. When n is equal to infinity, this RP phase reduces to a standard perovskite ABO₃ structure.

Among the families of perovskite and Ruddlesden–Popper oxides, lanthanide containing complex oxides draw a lot of interest because of their applications in many renewable energy devices. These applications include efficient catalysts, and electrodes for solid oxide fuel cells (SOFCs) and solid oxide electrolyser cells (SOECs).^6–12 The materials are found to be mixed ionic-electronic conductors (MIEC) and can catalyse the oxygen reduction reaction (ORR) at elevated temperatures (∼600 °C or higher). Combining the mixed conductivity and catalytic properties, they can improve the performance of a SOFC by expanding the active sites at the cathode from the triple phase boundaries between the cathode, electrolyte and gas to a much larger portion of the cathode–gas interface.¹³ As such, the electrocatalytic activity of these materials is important for their performance in electrochemical cells and is also of more general interest.

It is widely accepted that the exposed B-site transition metal ions in perovskite based oxides play the key role as the functional catalytical sites, owing to the ability of the transition metal atoms to change their valence and hence transfer electrons, e.g. in the ORR. However, a number of recent experimental discoveries introduce a different scenario. These experiments, which used highly surface-sensitive characterization techniques such as low energy ion scattering (LEIS) and scanning transmission electron microscopy (STEM), reveal that very few transition metal (B-site) atoms can be detected on the surfaces of these materials.^14–17 In the case of a Sr doped La₂NiO₄ single crystal, Burriel et al. used the LEIS technique and found a (001) surface dominated by La and Sr.¹⁴ Further X-ray photoelectron spectroscopy (XPS) results confirmed this La/Sr-rich surface and also discovered a Ni rich subsurface region extending to about 7 nm. Druce et al. conducted LEIS characterization on a number of polycrystalline materials,^15,16 including single perovskite La_0.6Sr_0.4Co_0.2Fe_0.8O_3−δ, double perovskite GdBaCo₂O_5+δ, and Ruddlesden–Popper phases La₂NiO_4+δ, PrLaNiO_4+δ and Pr₂NiO_4+δ. In all cases, the sample surfaces are consistently found to be mainly terminated with A-site elements (lanthanides, Ba or Sr). More recently, Chen et al. looked at the epitaxial thin-film of Ruddlesden–Popper (La_1−xSr_x)₂CoO₄ using high resolution STEM and atomic force microscopy (AFM) methods.¹⁷ At both (001) and (100) orientations, La/Sr-rich surfaces were found, together with the evidence of Sr segregation. These findings agreed with the LEIS surface characterisation results and depth profiling reported in the same work. All the materials examined in these experimental studies are known oxygen reduction catalysts in SOFC applications. These discoveries altogether sparked interest to explore the oxygen reduction mechanism of these lanthanide and alkaline earth rich surfaces.

A few modelling attempts have been made to explore and understand this problem. Notably, Akbay et al. used ab initio simulation and nudged elastic band (NEB) transition state search methods to study the oxygen reduction and dissociation on the LaO-terminated (001) planes of stoichiometric La₂NiO₄.¹⁸ Density functional theory with the on-site Hubbard U parameter (DFT + U) was employed in this study to properly address the strong correlation effect in La₂NiO₄ due to the transition metal Ni. The calculated energy barrier for the oxygen dissociation reaction on the La–La bridge site was reported to be 1.095 eV. Under such a small reaction barrier, it is certainly viable for the activated oxygen to dissociate on the exposed La ions. This result suggested that lanthanum atoms may not be as inert as previously expected. Comparing the oxygen dissociation barrier on La (1.095 eV) to an earlier report of the calculated oxygen dissociation barrier on the equivalent Sr site (3.4 eV) of a pristine SrTiO₃ surface by Staykov et al.,¹⁹ a clear difference can be seen between the oxygen reduction behaviour of exposed Sr ions and La ions. A careful review of their results reveals that, unlike the +2 atomic charge of the Sr ion, the surface La ions have a charge much different from the formal charge of +3. Akbay et al.'s study is not the only theoretical report where the La ion does not show a +3 charge in its oxides. Other studies by Ritzman et al. and Lee et al. also suggest that La ions take atomic charges of about +2 in related oxides.^20–22 Ritzman et al. studied the defect chemistry of La_0.5Sr_0.5Co_0.25Fe_0.75O_3−δ and La_1−xSr_xFeO_3−δ using plane-wave based DFT + U methods.^20,22 In addition to the focus on the structural and chemical effects of different levels of cation doping and oxygen vacancies, they also reported calculated Bader atomic charges of the atoms. In each of the defect levels, La atoms consistently give a Bader atomic charge ranging from +2.06 to +2.10. Similarly, in Lee et al.’s DFT/DFT + U study on the LaAlO₃ and LaMnO₃ systems, Bader charge analyses gave La charges of +2.04 to +2.07.²¹ These unusual atomic charges of La atoms are very interesting as these may be related to the oxygen reduction activity of the La-terminated surfaces. The origin of these La atomic charges calculated is also well worth investigation.

In this work, multiple but different levels of DFT and Hartree–Fock based simulations have been used to examine the electronic configuration of the La ion in its oxides to understand the origin of its unusual atomic charge. The atomic charges of the Sr, Pr and Ba ions in their related oxides have also been studied for comparison. The electron density maps of two prototypical perovskite oxides, LaAlO₃ and SrTiO₃, were characterised with synchrotron X-ray diffraction to directly validate simulation results. The relationships between the electronic configurations, atomic charges and catalytic behaviour are explored. In addition, the traditional concept of “ionicity” in solid is briefly reviewed and adapted. The proposed adaption of the theoretical atomic ionicity in solids can be a useful descriptor for the general evaluation and understanding of the catalytic performances of complex oxides containing lanthanide elements.

Computational details

A number of La, Pr, Sr and Ba containing oxides are selected for investigation. The materials studied include LaAlO₃, La₂O₃, SrTiO₃, SrO, PrAlO₃, Pr₂O₃, BaTiO₃ and BaO. This selection covers both simple binary and complex ternary oxides. The structural lattices of each of these materials are relaxed based on their experimentally determined crystallographic unit cells^23–29 using both, for comparison, the generalized gradient approximation (GGA) parameterized by Perdew–Burke–Ernzerhof (PBE)^30,31 and the related hybrid functional (PBE0).³² A summary of the comparison between the calculated and experimental lattice parameters of the oxides is included in the ESI.† The electronic structures of the materials are then calculated using the relaxed geometry with the PBE and PBE0 functionals respectively. In addition, Hartree–Fock calculations of the relaxed La and Sr containing materials are included as an example to demonstrate the maximum possible error ranges in charge analyses, as this theoretical approximation is highly inappropriate for the studied system. The Hartree–Fock method uses a mean field approximation for the description of the electron densities and does not account for electron correlation effects. Therefore, the Hartree–Fock calculations are expected to give significantly less accurate results compared to the GGA–DFT or hybrid DFT methods and may be used as a case for maximum error range estimation. To further compare and study the effects on the computed atomic charge due to different theoretical approaches, all the calculations were carried out using both the atomic centred Gaussian basis sets and plane wave basis sets separately. Finally, the projected density of states of the s orbitals and d orbitals for La, Sr, Pr and Ba ions obtained from their respective DFT calculations are plotted for comparison.

The calculations based on the Gaussian basis sets are conducted using the CRYSTAL14 software package^33,34 with linear combinations of atomic orbital (LCAO) basis sets. In the LCAO basis sets used, the core electrons of the La, Sr, Pr and Ba atoms are described with quasi-relativistic pseudopotentials,^35,36 while the valence electrons are described using 411p(411)d(311)f(1) contract sets (for La),^37,38 211d(11)f(1) contract sets (for Sr),³⁹ 3111p(3111)d(211)f(11) contract sets (for Pr)^36,37,40 and 31d(1) contract sets (for Ba)⁴¹ respectively. The Al, Ti and O LCAO basis sets used are triple-zeta-valence all-electron basis sets as employed in previous work.^38,42 These basis sets have been proven to give accurate description of solid oxide materials.^37–42 The cut-off threshold parameters for the summation of the Coulomb and exchange series are set to be 7, 7, 7, 7 and 14 as detailed in the CRYSTAL14 manual.³³ A Monkhorst–Pack mesh with a shrinking factor of 8 is used for reciprocal space sampling across all calculations using LCAO basis sets to ensure sufficiently dense k-point sampling. The atomic charges of the La, Sr, Pr, Ba and O ions are calculated using Mulliken charge analysis⁴³ from the DFT calculations using LCAO basis sets, based on the relaxed structures of the studied compounds.

The plane wave DFT simulations are calculated with the Vienna Ab initio Simulation Package (VASP).^44–47 The projector augmented-wave (PAW) pseudopotential based basis sets supplied in the VASP package were used with an energy cut-off value of 500 eV.^48,49 A 4 × 4 × 4 gamma-centred k-points mesh is used to sample the reciprocal space during the plane wave DFT calculations to properly simulate the anisotropic triclinic and hexagonal cells. Spin polarized calculations have been done in all cases. The atomic charges of the La, Sr, Pr, Ba and O ions are calculated using the Bader charge analysis⁴³ algorithm developed and implemented by Arnaldsson et al. from the plane wave DFT calculated charge densities.^50–52

Experimental methods

Sample preparation

Both oxides were prepared with the conventional solid state reaction method by using oxide and carbonate as the starting materials. In the case of LaAlO₃, La₂O₃ (99.9% purity, Wako) and Al₂O₃ (99.5%, Wako) were mixed using an alumina mortar and pestle. The obtained powder was heated in air at 1200 °C for 10 h. In the case of SrTiO₃, SrCO₃ (reagent class, Wako) was mixed with TiO₂ (99.5%, Wako) using an alumina mortar and pestle and then heated at 1173 °C for 10 h in air.

Synchrotron XRD measurements and data analysis

Synchrotron X-ray powder diffraction (XRD) measurements were conducted for LaAlO₃ and SrTiO₃ using a Debye–Scherrer camera with an imaging plate on beam line BL19B2 at SPring-8 (27 °C; wavelength = 0.4994152(11) Å). Structural analyses were carried out by the Rietveld method using RIETAN-FP.⁵³ The refined unit-cell parameters agree with those determined by the Le Bail method from the laboratory-based X-ray powder diffraction data using silicon powder as the internal standard within 2σ, where σ is the estimated standard deviation. The electron-density distributions of LaAlO₃ and SrTiO₃ were studied by the maximum-entropy method (MEM) using computer program Dysnomia.⁵⁴ The crystal structure and the electron-density distribution were visualized by the VESTA visualization package.⁵⁵

Results and discussion

It is well known that there is some ambiguity in the understanding and interpretation of atomic charges in solids. This ambiguity is mainly due to the wave-particle duality of the electron and the dynamic nature of chemical bonding in compounds. From the perspectives of quantum mechanics, there are only charge density distributions but not individually assigned charges. Some degrees of charge density overlap exist in most ionic solids. This charge density map is able to be experimentally determined by X-ray diffraction techniques, as reviewed thoroughly by Koritsanszky and Coppens.⁵⁶ The charge density map is also able to be calculated using ab initio theoretical methods. On the other hand, the concept of individual atomic charge is useful in applications, as it helps to qualitatively understand and predict the charge related properties of the material, such as catalysis, defect formation and ionic conductivity. To generate the individually assigned atomic charges from the continuous charge density map, two different approaches have been developed to define, partition and calculate atomic charges in a compound. One approach summarizes the electron population on the local atomic wavefunctions, and the most common method using this approach is the Mulliken population analysis.⁴³ The other approach tries to partition the electron density around the atoms by finding the minima of the local electron density surface and assign the partition to the atom; a widely used example for this approach is the Bader charge analysis,⁵⁷ which arises from Bader's quantum theory of atoms in molecules (QTAIM).

Each of the above mentioned approaches has their own limitations. For the Mulliken method, linear combinations of atomic orbital basis sets are usually used to describe the local wavefunctions in practice. Therefore, the atomic charges obtained with this method depend on the quality of the basis sets. In extreme cases, extremely unphysical results can be calculated if the basis sets used are highly inappropriate. For the Bader method, on the other hand, the difficulty lies in the determination of the minima of the electron density distribution. This difficulty is especially relevant in complex compounds, where the electron density minima between the atoms are not clearly defined. Knowing these limitations, we calculated the La atomic charge using different levels of ab initio theories and different charge analysis methods. The results calculated with both Mulliken population analysis and Bader charge analysis are summarized and compared with literature data. The calculated atomic charges of La, Sr, Pr and Ba ions in their related oxides are summarised in Fig. 1 and 2 respectively. Some available data reported in the literature are also included for comparison. The detailed values of the calculated atomic charges of La, Sr, Pr, Ba and O ions in the oxides studied are listed in Tables S2–S5 in the ESI.† The results of the bench-mark calculations at the Hartree–Fock level are presented only for the La and Sr compounds in Tables S2 and S3† to illustrate the trend.

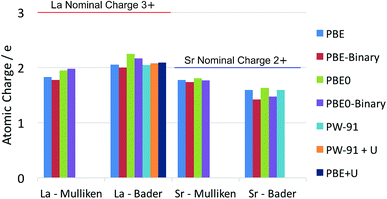Fig. 1 Summary of calculated atomic charges of La and Sr in their related oxides using different combinations of DFT and charge analysis methods. The ternary LaAlO₃ and SrTiO₃ oxides are calculated using both the GGA–PBE functional and the hybrid PBE0 functional. The results calculated for the La₂O₃ and SrO binary oxides are noted as PBE-Binary and PBE0-Binary in the figure. Literature results on LaAlO₃ (using PW-91 functional),²¹ LaMnO₃ (using PW-91 + U method),²¹ La_0.5Sr_0.5Co_0.25Fe_0.75O_3−δ (LSCF, using PBE + U method)²⁰ and SrTiO₃ (using PW-91 functional)²¹ are also included for comparison.

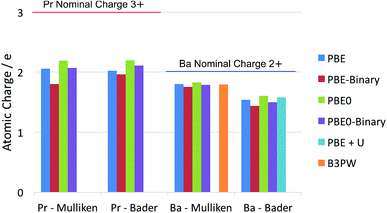Fig. 2 Summary of calculated atomic charges of Pr and Ba in their related oxides using different combinations of DFT and charge analysis methods. The ternary PrAlO₃ and BaTiO₃ oxides are calculated using both the GGA–PBE functional and the hybrid PBE0 functional. The results calculated for the Pr₂O₃ and BaO binary oxides are noted as PBE-Binary and PBE0-Binary in the figure. Literature results on BaTiO₃ (using the B3PW functional)⁵⁸ and Sm_0.5Ba_0.5CoO_2.75 (using the PBE + U method)⁵⁹ are also included.

The results in Fig. 1 and 2 show that the agreements between different ab initio approximations and charge analysis methods are reasonably good in most cases, owing to the developments of the basis sets and analysis methods in the past few decades. In the case of La atomic charge, the values calculated using the DFT methods range from 1.774 to 2.244 in different compounds. All the DFT calculated La atomic charges are much different from the La nominal formal charge of +3, which is usually assumed based on the La valence number. The results obtained with Hartree–Fock calculations in Table S2,† as expected, give higher values of La atomic charges ranging from 2.316 to 2.498. This is because the Hartree–Fock level of theory does not consider the electron correlations and hence overly localize the electrons. The significant difference between the average of the DFT results and the Hartree–Fock results suggests that the risk of incorrect interpretation still exists if a highly inappropriate approximation is used to study the material of interest. For the Sr charges in SrTiO₃ and SrO, the DFT calculated values range from 1.424 to 1.804. Unlike the calculated La atomic charges, these values are much closer to the Sr nominal formal charge of +2. Also, the Hartree–Fock results overestimate the Sr atomic charges to a less extent compared to the La calculations due to a weaker correlation effect in Sr compared to that in La.

Comparing the La and Pr calculated atomic charges presented in Fig. 1 and 2, the results show very similar atomic charges for the two lanthanides. The Pr ions, like the La ions, exhibit about +2 atomic charges instead of the usually assumed +3 valence number in their oxides. Looking at the Sr and Ba charges presented, it is understood that alkaline earth metals exhibit consistent charges of about +1.7 which is much closer to their valence number of +2.

The oxygen ionic charges are of much interest for the materials studied in this work, since many of them have applications as oxygen ionic conductors. The calculated charges associated with the oxygen ions differ a lot in different materials as shown in Tables S2–S5 of the ESI.† For the binary oxides, the computed oxygen charges vary around −1.2 to −1.8. The oxygen charges in SrO and BaO are generally more ionic than their counterparts in La₂O₃ and Pr₂O₃, as expected. In the perovskite oxides, oxygen charges are significantly affected by the B-site atoms and the simulation approaches. This is very clear when comparing the results of the La-containing perovskites listed in Table S2.† Looking at the oxygen charges computed with plane-wave basis sets and Bader charge analysis in LaMnO₃ and La_0.5Sr_0.5Co_0.25Fe_0.75O_3−δ (LSCF), it is apparent that the oxygen atoms have significant electron density overlaps with the transition metal atoms at the B-sites. Particularly, the oxygen charge is reduced to about −1.1 in the LSCF perovskite. As the LSCF perovskite is one of the best performing SOFC cathode materials available, the implication of the calculated O⁻ ions in LSCF certainly needs more attention in the future.

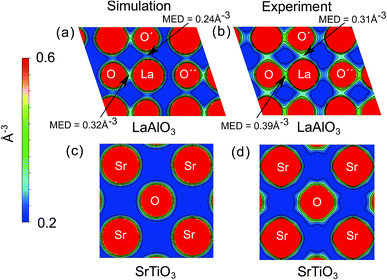
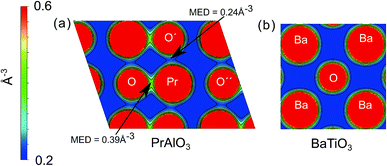
To obtain an intuitive understanding of the electronic interactions between the atoms in the materials studied, the electron density maps of the perovskites studied (LaAlO₃, SrTiO₃, PrAlO₃ and BaTiO₃) have been visualized. For two of the prototypical perovskites, LaAlO₃ and SrTiO₃, the calculated electron density maps were further validated by the experimental electron density maps obtained with synchrotron X-ray diffraction. The experimental electron density maps were obtained from the diffraction data analyzed using the maximum entropy method.^60,61 The cross-sections of the electron density volumes are presented in Fig. 3 and 4. The (012) planes cutting through the La/Pr and O atoms are visualized due to the R3̄c symmetry of the LaAlO₃ and PrAlO₃ perovskites. For the cubic perovskites, SrTiO₃ and BaTiO₃, the (001) basal planes are illustrated.

Fig. 3 Simulated and experimental electron density distributions of selected oxides; (a) simulated electron density distribution on the (012) plane of LaAlO₃, (b) experimental electron density distribution on the (012) plane of LaAlO₃, (c) simulated electron density distribution on the (001) plane of SrTiO₃, (d) experimental electron density distribution on the (001) plane of SrTiO₃. The simulated electron densities were calculated using the PBE0 functional. MED refers to the minimum electron density at the point.

Fig. 4 Simulated electron density distributions of selected oxides; (a) simulated electron density distribution on the (012) plane of PrAlO₃, (b) simulated electron density distribution on the (001) plane of BaTiO₃. The simulated electron densities were calculated using the PBE0 functional. MED refers to the minimum electron density at the point.

As observed in both figures, the experimental electron density maps support the computational predictions and show clearly the anisotropic electron density overlap between the La and O atoms, a behavior shared by the Pr–O interaction in PrAlO₃. However, this interaction is not seen between the Sr–O or Ba–O atom pairs, both theoretically and experimentally. An earlier synchrotron XRD measurement by Kawamura et al. has shown a similar difference in the LaSrAlO₄ Ruddlesden–Popper material, where the La–O electronic interaction is stronger than the Sr–O electronic interaction.⁶² Quantitatively, the calculated La–O electron density overlap in LaAlO₃ was weaker than the one observed from the experiments. Such differences between the computational and experimental results have been reported in the literature, e.g. the Bi–O interaction studied in BiFeO₃ by Fujii et al.⁶¹ These simulation results and experimental observations confirm and partly explain the partial charge differences summarized in Fig. 1 and 2, where the extra electron on the lanthanide is shared between the lanthanide atom and its neighboring oxygen atoms.

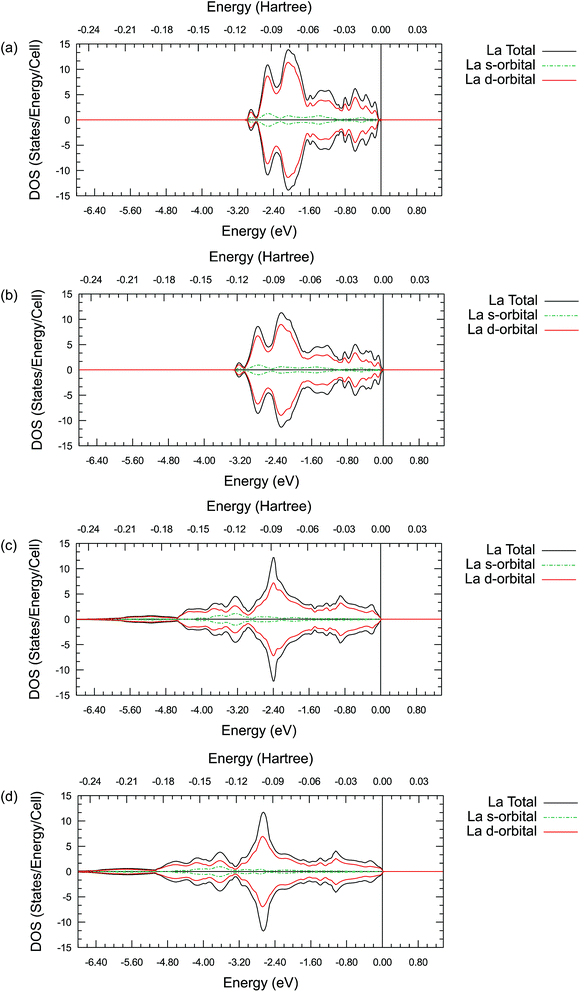
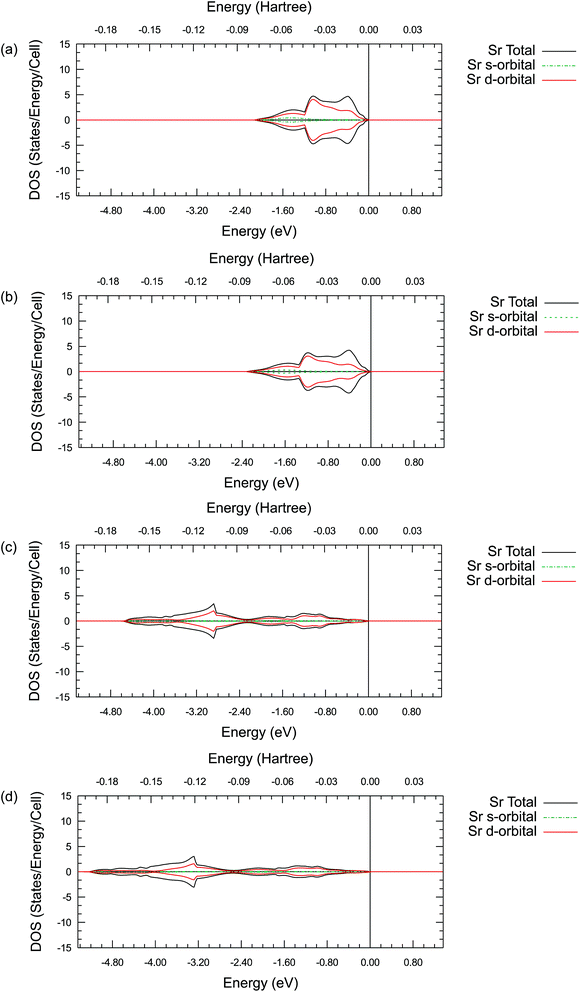
Summarizing all these results, it is clear that there is a difference between the valence electron interactions of the lanthanides and alkaline earth metals in their oxides. To further understand the possible origin of this difference and the detailed valence electronic structure of the ions studied, the projected density of states (DOS) are plotted for a single La, Sr, Pr or Ba ion. In addition, the partial density of states (PDOS) for the s-orbitals and d-orbitals are plotted together in the same figure respectively. These results are shown in Figure 5, 6, S1 and S2.†

By comparing the DOS plots, it can be seen that the results obtained using different ab initio approximations are consistent with each other for the valence bands, just like the consistency found in the atomic charge analysis. In Fig. 5(a)–(d), the PDOS clearly show that there is a significant occupied state on the valence d-orbital for the La ions. This suggests that there are valence d electrons staying on the La ions in these compounds. A particularly interesting point is that these occupied d-orbital states persist even in the simple binary La₂O₃ oxides, where it is natural to assume a highly ionic behaviour and resulting +3 La charge due to charge neutrality requirements. To fulfil the charge neutrality condition, the PDOS and charge analysis presented here hint at a significant level of covalency in the La₂O₃ compound. In Figure 6(a)–(d), no similar significant state occupancies are found for the Sr d-orbital PDOS near the Fermi level. Comparing Fig. 5 and S1,† similar Pr d-orbital occupancies, like the La case, are observed in the Pr PDOS plots of both Pr₂O₃ and PrAlO₃. In Fig. S2(c) and (d),† the Ba PDOS plots in BaTiO₃ have different shapes compared to the Sr PDOS plots (SrTiO₃) in Fig. 6(c) and (d). While the d-orbital occupancies are small in both the Sr and Ba cases, the total DOS peaks shown in Fig. S2(c) and (d)† are due to the states occupied by the 5p electron in Ba.

Fig. 5 Projected La density of states for its s-orbitals and d-orbitals in La₂O₃ (a and b) and LaAlO₃ (c and d). (a) and (c) are calculated using the GGA–PBE functional. (b) and (d) are calculated using the hybrid PBE0 functional. The Fermi energy is marked as 0 eV on the energy scale in all plots.

Fig. 6 Projected Sr density of states for its s-orbitals and d-orbitals in SrO (a and b) and SrTiO₃ (c and d). (a) and (c) are calculated using the GGA–PBE functional. (b) and (d) are calculated using the hybrid PBE0 functional. The Fermi energy is marked as 0 eV on the energy scale in all plots.

These PDOS results agree with our findings from the atomic charge analysis and show that the extra d electrons retained on the La ions and the Pr ions are responsible for the charge difference between lanthanides (La and Pr) and alkaline earth metals (Sr and Ba). Due to the shape and diffuse nature of the valence 5d orbitals, this extra d electron can interact with external molecules and may promote oxygen reduction reactions. Indeed, binary La₂O₃ with no transition metals has been reported for its catalytic activities in previous studies.^63,64 Moreover, Nicollet et al. reported significant surface oxygen reduction and exchange activity very recently for binary Pr₆O₁₁.⁶⁵ While Pr₆O₁₁ nominally contains a mixture of Pr(III) and Pr(IV) ions and is not quite the same as Pr₂O₃, a partially occupied diffuse valence orbital may still be responsible for the observed catalytic activity in Pr₆O₁₁. Combining the atomic charge analysis and the density of states plots, it is suggested that treating the La and Pr ions in their respective oxides as 2+ ions with significant covalency would be more appropriate, instead of viewing them as fully ionic 3+ ions. This new perspective may have important practical implications in the evaluation of the catalytic activity of the oxides of the lanthanide elements. While the synchrotron X-ray diffraction electron density mapping conducted in this work has validated the significant La–O covalency predicted in LaAlO₃, the proposed concept is certainly worth to be further confirmed experimentally in other lanthanide containing oxides.

A key problem of the conventional view of a La-containing oxide is that the atomic charge of La is assumed to be the same as its valence number. Based on this assumption, the La ions are believed to always behave as 3+ ions in La containing oxides, and this assumption guided the past materials engineering efforts to optimize the catalytic and transport properties of La-containing complex oxides. However, the results in this paper showed that this “atomic charge = valence number” assumption does not describe the behaviour of the La ions sufficiently. If one goes back to the IUPAC's formal definitions of “atomic charge” and “valence number”, the atomic charge is defined as follows:⁶⁶

“Atomic charge attributed to an atom A within a molecule defined as ζ = Z_A − q_A, where Z_A is the atomic number of A and q_A is the electron density assigned to A. The method of calculation of q_A depends on the choice of the scheme of partitioning electron density. In the framework of the Mulliken population analysis q_A is associated with the so-called gross atomic population: q_A = ∑q_μ, where q_μ is a gross population for an orbital μ in the basis set employed defined according to

where P_μν and S_μυ are the elements of density matrix and overlap matrix, respectively. In the Hückel molecular orbital theory (where S_μυ = δ_μυ), q_μ = n_μP_μμ, where n_μ is the number of electrons in the MO μ.”

However, the value of the valence number of an atomic species is defined as:⁶⁶

“The maximum number of univalent atoms (originally hydrogen or chlorine atoms) that may combine with an atom of the element under consideration, or with a fragment, or for which an atom of this element can be substituted”.

From the IUPAC definitions, it is very clear that these two concepts are quite different and should not be taken as the same. The valence number of an atomic species is a fixed integer, e.g. the valence number of La is 3 as La can form the compound LaF₃. On the other hand, the charge of an atom depends on its surrounding environment and may not be a fixed integer from the point of view of quantum mechanics. Taking the results reported here as examples again, the atomic charge of La in LaAlO₃ is approximately 2.0, much different from the La valence number of 3, while the atomic charge of Sr in SrTiO₃ is approximately 1.8, close to the Sr valence number of 2. The atomic charge of the atom or ion is hence the more important and relevant property when evaluating the functionality of complex oxides as catalysts or ionic conductors, as it is the atomic charge that determines how the atom actually interacts with other atoms or molecules, e.g. at the surface of the oxide. This understanding is especially relevant for the lanthanum or the lanthanide series, as these species can be considered to be very weak transition metals and should not be simply regarded as “inert”. As the electronic configuration of elemental La is [Xe]5d¹6s² while the electronic configuration of elemental Sr is [Kr]5s², it is not natural to assume the d electrons in La will behave the same way as the s electrons in La or Sr and just transfer to the oxygen ions in the oxides. The same trend may be applicable to other lanthanides, especially a few special ones: Ce (electronic configuration = [Xe]4f¹ 5d¹ 6s²), Gd (electronic configuration = [Xe]4f⁷ 5d¹ 6s²), Lu (electronic configuration = [Xe]4f¹⁴ 5d¹ 6s²) and also Hf (beyond the lanthanides but possessing an electronic configuration of [Xe]4f¹⁴ 5d² 6s²). These elements contain partially filled valence d-orbitals even as neutral atoms. A few experiments have already demonstrated catalytic activities of these elements proposed here. In addition to the catalytically active La₂O₃ (ref. 63 and 64) and Pr₆O₁₁ (ref. 65) materials mentioned earlier, Hf decorated perovskites have recently been reported to be catalytically active by Tsvetkov et al.⁶⁷

Considering that the common application of the oxides of these elements often involves catalysis and oxygen reduction, it is very useful to establish a way to quickly distinguish which metallic elements are more likely to be active than others. To achieve this goal, it is convenient to call back the old concept of “ionicity”. In many cases, if an element is catalytically active in a compound, this element will have diffuse valence electrons available for transfer. Thus, such an element tends to have a lower degree of ionicity, as the diffuse valence electron density will overlap with the electron density of other ions in the compound. However, the term “ionicity”, similar to the “atomic charge”, also has some ambiguity in its definition. Catlow and Stoneham gave an extensive review on the experimental and theoretical aspects of ionicity in solids in 1983.⁶⁸ As Catlow and Stoneham summarized, Pauling defined a thermochemically based ionicity scale using the formation energy of a molecule and the electron negativities of the component elements;⁶⁹ while Phillips' spectroscopic approach defines an ionicity scale by dividing the ‘total energy gap’ of a crystal (obtained from the optic dielectric constant) into a covalent gap and an ionic gap.⁷⁰ Both Pauling's and Phillips' approaches are derived more from the experimental perspective. Catlow and Stoneham's review also discussed the difficulties to obtain a consistent and unique atomic charge and subsequently ionicity from the charge density map theoretically. A major source of the ambiguity, as discussed at the beginning of this section, is that there are multiple valid theoretical definitions to partition the charge density, and these definitions usually do not result in a single universal atomic charge value.

While the ambiguity of charge density partition discussed by Catlow and Stoneham is somewhat inevitable, the developments of charge analysis methods and LCAO basis sets since the 1980s have significantly alleviated this problem. Particularly, Bader's quantum theory of atoms in molecules has established a regular framework to address the problem of charge density partition.⁵⁷ These developments allowed a qualitatively consistent and meaningful charge analysis in complex oxides as demonstrated in the results presented in this work. Due to the practical usefulness of the calculated ionicity in the context of common catalytic oxides, it is suggested that an adapted relative ionicity scale can be defined using the DFT calculated atomic charge and formal valence number as

where the valence number is defined as the formal IUPAC definition. Highly ionic elements, e.g. Mg in MgO, Sr in SrTiO₃ and Ba, have ionicities which are close to 1. The more active transition metals, e.g. Ti in SrTiO₃, have an ionicity much less than 1 (about 0.62 for Ti in SrTiO₃). The La atoms in many common La containing oxides, e.g. LaAlO₃, LaMnO₃, and La₂NiO₄ generally have an ionicity around 0.66. With a lower number of ionicity value, the atom considered is more likely to be polarized and active for catalysis/oxygen reduction. However, it is important to note that, as discussed earlier, the atomic charge values determined from charge densities in compounds will depend on the method. The ionicity value of an element will also vary in different compounds due to its local bonding environment. Still, if the basis sets and the methods used can properly reflect the important electronic properties of the compound, then the atomic charges calculated with the same basis sets and methods should be able to give a reasonable estimation of the atomic ionicity. Within this limit, the adapted ionicity definition suggested in this work should be able to help qualitative prediction of possible catalytic elements and guide substitution strategies for complex oxides tailored for energy applications.

Conclusions

In this work, we have calculated the atomic charges of La, Sr, Pr and Ba in their related oxides using different DFT approximations and charge analysis methods. By comparing the results obtained with different methods, we found that the calculated La and Pr atomic charges in their oxides are consistently close to +2 rather than +3 despite the inherent differences in the theoretical approaches used. Agreements between the synchrotron XRD generated and DFT calculated electron density maps of LaAlO₃ and SrTiO₃ have validated the theoretical predictions. By plotting projected partial density of states of the La, Sr, Pr and Ba ions in related compounds, we have shown that the presence of the occupied valence d-orbitals on the La and Pr ions is responsible for the extra charges on the La and Pr ions in oxides. On the other hand, the Sr and Ba ions do not possess significantly occupied valence d-orbitals in their respective oxides. This difference between the valence electronic structure of the lanthanide and alkaline earth metal ions can explain the catalytic activity of the lanthanide rich oxide surfaces and relatively inert behaviour of the Sr or Ba rich oxide surfaces.

Based on these results, we suggest that the calculated partially covalent La/Pr atomic charge of +2 is more appropriate to consider compared to the conventional picture of the fully ionic La/Pr 3+ ions. This perspective would be very useful in materials engineering and performance optimization, especially when optimizing these oxides for catalysing oxygen reduction reactions. In addition, the roles and electronic behaviour of other lanthanides, particularly those containing d electrons, should be carefully re-evaluated for catalytic reactions. Finally, after a brief review of the concept of “ionicity” in solids and a clarification of the concepts of valence number and atomic charge, we suggest an adaption of the term “ionicity in solids”. The adapted concept of ionicity is formulated as the ratio of an atom's calculated atomic charge to its valence number, based on specific quantum mechanical calculations of the atom in the materials of interest. The adapted ionicity concept can be used as a descriptor to identify a possibly polarized and catalytically active candidate among several structurally similar compounds containing different elements.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This project was supported by the Japan Society for the Promotion of Science (JSPS) and the National Science Foundation (NSF) under the JSPS-NSF Partnerships for International Research and Education (PIRE), and the Core-to-Core Program on Solid Oxide Interfaces for Faster Ion Transport (SOIFIT) funded by JSPS and EPSRC (grant no. EP/P026478/1). This work was also supported by the World Premier International Research Centre Initiative (WPI), Ministry of Education, Culture, Sports, Science, and Technology of Japan (MEXT). K. F. and M. Y. acknowledge the support by the Grant-in-Aid for Scientific Research (KAKENHI, No. JP15H02291, JP16H06293, JP16K21724, and JP17H06222) from the MEXT, Japan. The synchrotron experiments were carried out at SPring-8 (2017A1803 and 2017B1265).

References

1. K. Szot, W. Speier, G. Bihlmayer and R. Waser, Nat. Mater., 2006, 5, 312–320.
2. A. P. Ramirez, J. Phys.: Condens. Matter, 1997, 9, 8171–8199.
3. P. W. Anderson, G. Baskaran, Z. Zou and T. Hsu, Phys. Rev. Lett., 1987, 58, 2790–2793.
4. J. P. Attfield, A. L. Kharlanov and J. A. McAllister, Nature, 1998, 394, 157–159.
5. R. J. H. Voorhoeve, D. W. Johnson, J. P. Remeika and P. K. Gallagher, Science, 1977, 195, 827–833.
6. J. A. Kilner and M. Burriel, Annu. Rev. Mater. Res., 2014, 44, 365–393.
7. T. Ishihara, N. Sirikanda, K. Nakashima, S. Miyoshi and H. Matsumoto, J. Electrochem. Soc., 2010, 157, B141.
8. Perovskite Oxide for Solid Oxide Fuel Cells, ed. T. Ishihara, Springer, US, Boston, MA, 2009.
9. S. J. Skinner and J. A. Kilner, Solid State Ionics, 2000, 135, 709–712.
10. G. Amow and S. J. Skinner, J. Solid State Electrochem., 2006, 10, 538–546.
11. T. Ishihara and H. Furutani, Chem. Mater., 1999, 11, 2081–2088.
12. X. Yang and J. T. S. Irvine, J. Mater. Chem., 2008, 18, 2349.
13. S. B. Adler, J. A. Lane and B. C. H. Steele, J. Electrochem. Soc., 1996, 143, 3554.
14. M. Burriel, S. Wilkins, J. P. Hill, M. A. Muñoz-Márquez, H. H. Brongersma, J. A. Kilner, M. P. Ryan and S. J. Skinner, Energy Environ. Sci., 2014, 7, 311.
15. J. Druce, H. Téllez, M. Burriel, M. D. Sharp, L. J. Fawcett, S. N. Cook, D. S. McPhail, T. Ishihara, H. H. Brongersma and J. A. Kilner, Energy Environ. Sci., 2014, 7, 3593–3599.
16. J. Druce, T. Ishihara and J. A. Kilner, Solid State Ionics, 2014, 262, 893–896.
17. Y. Chen, H. Téllez, M. Burriel, F. Yang, N. Tsvetkov, Z. Cai, D. W. McComb, J. A. Kilner and B. Yildiz, Chem. Mater., 2015, 150630082136008.
18. T. Akbay, A. Staykov, J. Druce, H. Téllez, T. Ishihara and J. A. Kilner, J. Mater. Chem. A, 2016, 4, 13113–13124.
19. A. Staykov, H. Téllez, T. Akbay, J. Druce, T. Ishihara and J. A. Kilner, Chem. Mater., 2015, 27, 8273–8281.
20. A. M. Ritzmann, J. M. Dieterich and E. A. Carter, Phys. Chem. Chem. Phys., 2016, 18, 12260–12269.
21. Y.-L. Lee and D. Morgan, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 195430.
22. A. M. Ritzmann, A. B. Muñoz-García, M. Pavone, J. A. Keith and E. A. Carter, Chem. Mater., 2013, 25, 3011–3019.
23. J. Bashir, R. T. A. Khan, N. M. Butt and G. Heger, Powder Diffr., 2002, 17, 222.
24. Y. A. Abramov, V. G. Tsirelson, V. E. Zavodnik, S. A. Ivanov and I. D. Brown, Acta Crystallogr., 1995, 51, 942–951.
25. H. Lehnert, B. Boysen, S. J. Schneider, F. Frey, D. Hohlwein, P. Radaelli and H. Ehrenberg, Z. Kristallogr., 2000, 215, 536.
26. J. Zhao, N. L. Ross, R. J. Angel, M. A. Carpenter, C. J. Howard, D. A. Pawlak and T. Lukasiewicz, J. Phys.: Condens. Matter, 2009, 21, 235403.
27. W. C. Koehler and E. O. Wollan, Acta Crystallogr., 1953, 6, 741–742.
28. G. H. Kwei, A. C. Lawson, S. J. L. Billinge and S. W. Cheong, J. Phys. Chem., 1993, 97, 2368–2377.
29. M. A. Ghebouli, B. Ghebouli, A. Bouhemadou, M. Fatmi and K. Bouamama, J. Alloys Compd., 2011, 509, 1440–1447.
30. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
31. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 4978.
32. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985.
33. R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D'Arco, M. Llunell, M. Causà and Y. Noël, CRYSTAL14 User's Manual, University of Torino, Torino, 2014.
34. R. Dovesi, R. Orlando, A. Erba, C. M. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. De La Pierre, P. D'Arco, Y. Noël, M. Causà, M. Rérat and B. Kirtman, Int. J. Quantum Chem., 2014, 114, 1287–1317.
35. W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298.
36. M. Dolg, H. Stoll, A. Savin and H. Preuss, Theor. Chim. Acta, 1989, 75, 173–194.
37. J. Yang and M. Dolg, Theor. Chem. Acc., 2005, 113, 212–224.
38. J. Wu, S. S. Pramana, S. J. Skinner, J. A. Kilner and A. P. Horsfield, J. Mater. Chem. A, 2015, 3, 23760–23767.
39. A. Erba, K. E. El-Kelany, M. Ferrero, I. Baraille and M. Rérat, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 35102.
40. A. Weigand, X. Cao, J. Yang and M. Dolg, Theor. Chem. Acc., 2010, 126, 117–127.
41. G. Sophia, P. Baranek, C. Sarrazin, M. Rérat and R. Dovesi, Phase Transitions, 2013, 86, 1069–1084.
42. E. A. Ahmad, L. Liborio, D. Kramer, G. Mallia, A. R. Kucernak and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 85137.
43. R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833.
44. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
45. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
46. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
47. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
48. G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
49. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
50. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 84204.
51. M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 134, 64111.
52. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360.
53. F. Izumi and K. Momma, Solid State Phenom., 2007, 130, 15–20.
54. K. Momma, T. Ikeda, A. A. Belik and F. Izumi, Powder Diffr., 2013, 28, 184–193.
55. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
56. T. S. Koritsanszky and P. Coppens, Chem. Rev., 2001, 101, 1583–1628.
57. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
58. S. Piskunov, E. Heifets, R. I. Eglitis and G. Borstel, Comput. Mater. Sci., 2004, 29, 165–178.
59. E. Olsson, X. Aparicio-Anglès and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2017, 19, 13960–13969.
60. Y. Kuroiwa, S. Aoyagi, A. Sawada, J. Harada, E. Nishibori, M. Takata and M. Sakata, Phys. Rev. Lett., 2001, 87, 217601.
61. K. Fujii, H. Kato, K. Omoto, M. Yashima, J. Chen and X. Xing, Phys. Chem. Chem. Phys., 2013, 15, 6779–6782.
62. K. Kawamura, M. Yashima, K. Fujii, K. Omoto, K. Hibino, S. Yamada, J. R. Hester, M. Avdeev, P. Miao, S. Torii and T. Kamiyama, Inorg. Chem., 2015, 54, 3896–3904.
63. M. S. Palmer, M. Neurock and M. M. Olken, J. Phys. Chem. B, 2002, 106, 6543–6547.
64. O. V. Manoilova, S. G. Podkolzin, B. Tope, J. Lercher, E. E. Stangland, J. Goupil and B. M. Weckhuysen, J. Phys. Chem. B, 2004, 108, 15770–15781.
65. C. Nicollet, A. Flura, V. Vibhu, A. Rougier, J.-M. Bassat and J.-C. Grenier, Int. J. Hydrogen Energy, 2016, 41, 15538–15544.
66. IUPAC Compendium of Chemical Terminology, ed. M. Nič, J. Jirát, B. Košata, A. Jenkins and A. McNaught, IUPAC, Research Triagle Park, NC, 2009.
67. N. Tsvetkov, Q. Lu, L. Sun, E. J. Crumlin and B. Yildiz, Nat. Mater., 2016, 15, 1010–1016.
68. C. R. A. Catlow and A. M. Stoneham, J. Phys. C: Solid State Phys., 1983, 16, 4321–4338.
69. L. Pauling and J. C. Phillips, Phys. Today, 1971, 24, 9–15.
70. J. C. Phillips, Rev. Mod. Phys., 1970, 42, 317–356.

---

Footnote

† Electronic supplementary information (ESI) available: A summary and comparison of experimental and calculated lattice parameters of all the materials studied (Table S1), the detailed lists of calculated La, Sr, Pr, Ba and O atomic charges (Tables S2–S5) and the plotted density of states of Pr and Ba (Fig. S1 and S2) in their related oxides studied in this work are supplied. See DOI: 10.1039/c8ta01191e

---